Đề thi vào 10 môn Toán Phú Yên năm 2018Tải vềI. TRẮC NGHIỆM (3 điểm) Học sinh chọn một phương án đúng nhất ở mỗi câu và viết phương án chọn vào bài làm: Câu 1: Tìm x để biểu thức Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài I. TRẮC NGHIỆM (3 điểm) Học sinh chọn một phương án đúng nhất ở mỗi câu và viết phương án chọn vào bài làm: Câu 1: Tìm x để biểu thức \(\dfrac{1}{{\sqrt {{{\left( {x - 2} \right)}^2}} }}\) có nghĩa. A. \(x \ge 2\) B. \(x > 2\) C. \(x \ne - 2\) D. \(x \ne 2\) Câu 2: Hàm số nào sau đây là hàm số bậc nhất? A. \(y = ax + b\) B. \(y = 1 - 2x\) C. \(y = {x^2} + 1\) D. \(y = \dfrac{1}{x}\) Câu 3: Cặp số nào sau đây không phải là nghiệm của phương trình \(x + 2y = - 1?\) A. \(\left( {1; - 1} \right)\) B. \(\left( { - 1;\;0} \right)\) C. \(\left( {0;\;\dfrac{1}{2}} \right)\) D. \(\left( {3; - 2} \right)\) Câu 4: Hệ phương trình nào sau đây vô nghiệm? A. \(\left\{ \begin{array}{l}y = 2x - 3\\y = x + 5\end{array} \right.\) B. \(\left\{ \begin{array}{l}y = 2x - 3\\y = 2x + 1\end{array} \right.\) C. \(\left\{ \begin{array}{l}y = 2x - 3\\y = 4x - 6\end{array} \right.\) D. \(\left\{ \begin{array}{l}y = 2x - 3\\y = - x + 3\end{array} \right.\) Câu 5: Cho hàm số \(y = a{x^2}\;\;\left( {a > 0} \right).\) Kết luận nào sau đây là đúng? A. Hàm số đồng biến với mọi \(x.\) B. Hàm số nghịch biến với mọi \(x.\) C. Hàm số đồng biến khi \(x > 0.\) D. Hàm số nghịch biến khi \(x > 0.\) Câu 6: Phương trình nào sau đây có hai nghiệm phân biệt? A. \({x^2} + 3x - 4 = 0.\) B. \({x^2} + 2x + 1 = 0\) C. \({x^2} + x + 1 = 0\) D. \({x^2} + 1 = 0\) Câu 7: Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 2, HC = 4. Đặt BH = x. Tính x. A. \(x = \dfrac{1}{2}\) B. \(x = 1\) C. \(x = \dfrac{{16}}{3}\) D. \(x = 4\)
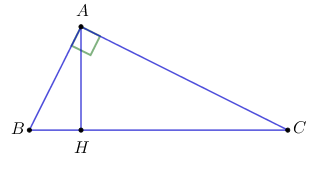
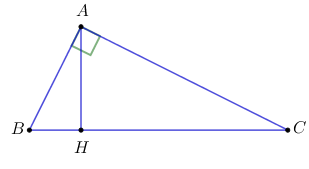
Câu 8: Cho tam giác ABC vuông tại A, đường cao AH. Đẳng thức nào sau đây là sai? A. \(\sin B = \dfrac{{AH}}{{AB}}\) B. \(\tan \widehat {BAH} = \dfrac{{BH}}{{AH}}\) C. \(\cos C = \dfrac{{HC}}{{AC}}\) D. \(\cot \widehat {HAC} = \dfrac{{AH}}{{AC}}\)
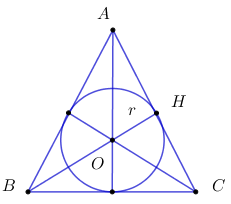
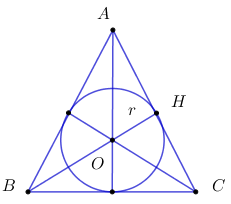
Câu 9: Tính chu vi C của tam giác đều ABC ngoại tiếp đường tròn có bán kính bằng \(\sqrt 3 cm.\) A. \(C = 9cm\) B. \(C = 9\sqrt 3 cm\) C. \(18cm\) D. \(18\sqrt 3 cm\)
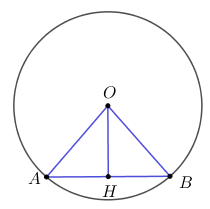
Câu 10: Cho đường tròn tâm O đường kính 10cm. Gọi H là trung điểm của dây AB. Tính độ dài đoạn OH, biết AB = 6cm. A. \(OH = 4cm\) B. \(OH = 8cm\) C. \(OH = 16cm\) D. \(OH = 64cm\)
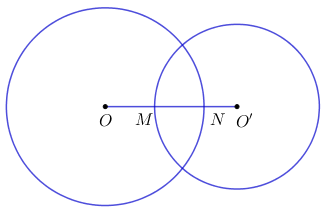
Câu 11: Cho đường tròn \(\left( {O;\;6cm} \right)\) và đường tròn \(\left( {O';\;5cm} \right)\) có đoạn nối tâm \(OO' = 8cm.\) Biết đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt \(OO'\) lần lượt tại \(N,\;M.\) Tính độ dài \(MN.\) A. \(MN = 4cm\) B. \(MN = 3cm\) C. \(MN = 2cm\) D. \(MN = 1cm\)
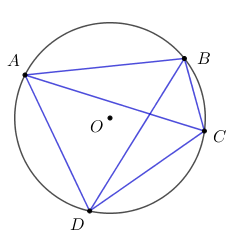
Câu 12: Cho tứ giác ABCD nội tiếp đường tròn tâm O. Khẳng định nào sau đây không đúng? A. \(\widehat {ADC} = \widehat {CBA}\) B. \(\widehat {ADB} = \widehat {ACB}\) C. \(\widehat {ADC} + \widehat {ABC} = {180^0}\) D. \(\widehat {DAB} + \widehat {DCB} = {180^0}\)
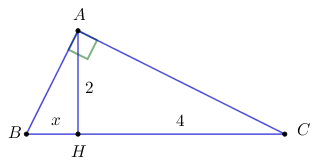
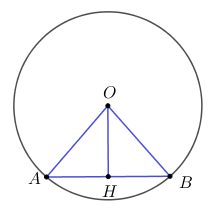
II. TỰ LUẬN (7 ĐIỂM) Câu 13 (1,50 điểm) a) So sánh 5 và \(2\sqrt 6 \) b) Giải phương trình \({x^4} - 4{x^2} - 5 = 0\) Câu 14 (1,50 điểm) Cho phương trình \(4{x^2} - 2\left( {m + 1} \right)x + {m^2} = 0\,\) (m là tham số) a) Với giá trị nào của m thì phương trình có nghiệm kép? b) Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình. Câu 15 (2,00 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình Nếu mở cả hai vòi nước chảy vào một bể cạn thì sau 3 giờ bể đầy nước. Nếu mở riêng từng vòi thì vòi thứ nhất làm đầy bể nhanh hơn vòi thứ hai là 2 giờ 30 phút. Hỏi nếu mở từng vòi thì mỗi vòi chảy bao lâu đầy bể. Câu 16 (2,00 điểm) Cho đường tròn \(\left( {O;R} \right)\) đường kính AB. Gọi d là tiếp tuyến của đường tròn tại A, C là điểm chuyển động trên đường thẳng d. BC cắt (O) tại D \(\left( {D \ne B} \right)\). Gọi E là trung điểm của BD. a) Chứng minh OACE là tứ giác nội tiếp. b) Chứng minh rằng \(BE.BC = 2{R^2}\) c) Tìm tập hợp các tâm I của đường tròn ngoại tiếp tam giác ACE. Đề bài Câu 1: Phương pháp: +) Biểu thức \(y = \dfrac{1}{{\sqrt {{f^2}\left( x \right)} }}\) có nghĩa \( \Leftrightarrow {f^2}\left( x \right) > 0 \Leftrightarrow f\left( x \right) \ne 0.\) Cách giải: Tìm x để biểu thức \(\dfrac{1}{{\sqrt {{{\left( {x - 2} \right)}^2}} }}\) có nghĩa. A. \(x \ge 2\) B. \(x > 2\) C. \(x \ne - 2\) D. \(x \ne 2\) Biểu thức \(\dfrac{1}{{\sqrt {{{\left( {x - 2} \right)}^2}} }}\) có nghĩa \( \Leftrightarrow {\left( {x - 2} \right)^2} > 0 \Leftrightarrow x - 2 \ne 0 \Leftrightarrow x \ne 2.\) Chọn D. Câu 2: Phương pháp: Hàm số bậc nhất là hàm số có dạng \(y = ax + b\;\;\left( {a \ne 0} \right).\) Cách giải: Hàm số nào sau đây là hàm số bậc nhất? A. \(y = ax + b\) B. \(y = 1 - 2x\) C. \(y = {x^2} + 1\) D. \(y = \dfrac{1}{x}\) Theo khái niệm hàm số thì đáp án B đúng. Chọn B. Câu 3: Phương pháp: Thay từng cặp số trong mỗi đáp án vào phương trình. Cặp nào thỏa mãn phương trình thì là nghiệm của phương trình trên. Cách giải: Cặp số nào sau đây không phải là nghiệm của phương trình \(x + 2y = - 1?\) A. \(\left( {1; - 1} \right)\) B. \(\left( { - 1;\;0} \right)\) C. \(\left( {0;\;\dfrac{1}{2}} \right)\) D. \(\left( {3; - 2} \right)\) Đáp án A: \(1 + 2.\left( { - 1} \right) = - 1 \Rightarrow \) A thỏa mãn. Đáp án B: \( - 1 + 2.0 = - 1 \Rightarrow \) B thỏa mãn. Đáp án C: \(0 + 2.\dfrac{1}{2} = 1 \ne - 1 \Rightarrow \) C không thỏa mãn. Chọn C. Câu 4: Phương pháp: Xét trong các đáp án ta thấy hệ phương trình có dạng: \(\left\{ \begin{array}{l}y = {a_1}x + {b_1}\;\;\;\left( {{d_1}} \right)\\y = {a_2}x + {b_2}\;\;\;\left( {{d_2}} \right)\end{array} \right..\) \( \Rightarrow \) Nghiệm của hệ phương trình là số giao điểm của đường thẳng \({d_1},\;\;{d_2}.\) \( \Rightarrow \) Hệ phương trình vô nghiệm \( \Leftrightarrow {d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Cách giải: Hệ phương trình nào sau đây vô nghiệm? A. \(\left\{ \begin{array}{l}y = 2x - 3\\y = x + 5\end{array} \right.\) B. \(\left\{ \begin{array}{l}y = 2x - 3\\y = 2x + 1\end{array} \right.\) C. \(\left\{ \begin{array}{l}y = 2x - 3\\y = 4x - 6\end{array} \right.\) D. \(\left\{ \begin{array}{l}y = 2x - 3\\y = - x + 3\end{array} \right.\) Nhìn vào các đáp án trên chỉ có đáp án B có \(\left\{ \begin{array}{l}{a_1} = {a_2} = 2\\{b_1} = - 3 \ne 1 = {b_2}\end{array} \right. \Rightarrow \) hệ phương trình \(\left\{ \begin{array}{l}y = 2x - 3\\y = 2x + 1\end{array} \right.\) vô nghiệm. Chọn B Câu 5: Phương pháp: Xét hàm số \(y = a{x^2}\) có: +) Với \(a > 0\) thì hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0.\) +) Với \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0.\) Cách giải: Cho hàm số \(y = a{x^2}\;\;\left( {a > 0} \right).\) Kết luận nào sau đây là đúng? A. Hàm số đồng biến với mọi \(x.\) B. Hàm số nghịch biến với mọi \(x.\) C. Hàm số đồng biến khi \(x > 0.\) D. Hàm số nghịch biến khi \(x > 0.\) Xét hàm số \(y = a{x^2}\) có: +) Với \(a > 0\) thì hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0.\) Chọn C. Câu 6: Phương pháp: Phương trình \(a{x^2} + bx + c = 0\;\;\left( {a \ne 0} \right)\)có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\) Cách giải: Phương trình nào sau đây có hai nghiệm phân biệt? A. \({x^2} + 3x - 4 = 0.\) B. \({x^2} + 2x + 1 = 0\) C. \({x^2} + x + 1 = 0\) D. \({x^2} + 1 = 0\) +) Đáp án A có: \(\Delta = {3^2} + 4.4 = 9 + 16 = 25 > 0 \Rightarrow \) phương trình có hai nghiệm phân biệt. Chọn A. Câu 7: Phương pháp: Sử dụng hệ thức lượng trong tam giác vuông: \(A{H^2} = BH.HC.\) Cách giải:
Ta có: \(A{H^2} = BH.HC \Leftrightarrow {2^2} = x.4 \Leftrightarrow x = 1.\) Chọn B. Câu 8: Phương pháp: Sử dụng các công thức hệ thức lượng của góc nhọn trong tam giác vuông để chọn đáp án đúng. Cách giải:
Xét tam giác \(ABH\) vuông tại \(H\) có: \(\sin B = \dfrac{{AH}}{{AB}} \Rightarrow \) đáp án A đúng. \(\tan \widehat {BAH} = \dfrac{{BH}}{{AH}} \Rightarrow \) đáp án B đúng. Xét tam giác \(AHC\) vuông tại \(H\) có: \(\cos C = \dfrac{{HC}}{{AC}} \Rightarrow \) đáp án C đúng. \(\cot \widehat {HAC} = \dfrac{{AH}}{{HC}} \Rightarrow \) đáp án D sai. Chọn D. Câu 9: Phương pháp: Áp dụng tính chất của đường trung tuyến và định lý Pi-ta-go để tính độ dài các cạnh của tam giác. Chu vi tam giác \(ABC\) là: \(C = AB + BC + CA.\) Cách giải:
Gọi O là tâm đường tròn nội tiếp tam giác đều \(ABC.\) Khi đó O cũng là trọng tâm tam giác ABC. \( \Rightarrow OH = \dfrac{1}{3}BH\) (tính chất đường trung tuyến trong tam giác). \( \Rightarrow BH = 3OH = 3r = 3\sqrt 3 cm.\) Áp dụng định lý Pi-ta-go đối với tam giác vuông \(BHC\) vuông tại \(H\) ta có: \(\begin{array}{l}\;\;\;\;B{C^2} = B{H^2} + H{C^2}\\ \Leftrightarrow B{C^2} = B{H^2} + {\left( {\dfrac{{BC}}{2}} \right)^2}\\ \Leftrightarrow \dfrac{3}{4}B{C^2} = {\left( {3\sqrt 3 } \right)^2}\\ \Leftrightarrow B{C^2} = 36\\ \Leftrightarrow BC = 6.\end{array}\) Chu vi tam giác đều \(ABC\) là: \(C = 3.BC = 3.6 = 18\;cm.\) Chọn C. Câu 10: Phương pháp: Sử dụng định lý Pi-ta-go để tính độ dài đoạn thẳng OH. Cách giải:
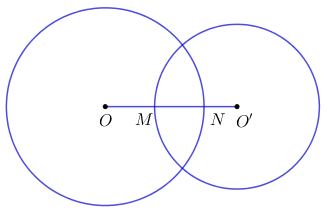
Xét đường tròn (O) ta có H là trung điểm của dây cung AB \( \Rightarrow OH \bot AB = \left\{ H \right\}\) (mối liên hệ giữa đường kính và dây cung). Áp dụng định lý Pi-ta-go cho tam giác \(OAH\) vuông tại H có: \(\begin{array}{l}O{H^2} = O{A^2} - A{H^2} = {R^2} - {\left( {\dfrac{{AB}}{2}} \right)^2} = {5^2} - {3^2} = {4^2}\\ \Rightarrow OH = 4cm.\end{array}\) Chọn A. Câu 11: Phương pháp: Sử dụng các công thức cộng đoạn thẳng. Cách giải:
Ta có: \(ON = 6cm,\;O'M = 5cm.\) \(\begin{array}{l}ON = OM + MN \Leftrightarrow 6 = OM + MN.\\O'M = O'N + MN \Leftrightarrow 5 = O'N + MN.\\ \Rightarrow 11 = OM + MN + O'N + MN \Leftrightarrow 11 = OM + O'N + 2MN.\end{array}\) Lại có: \(OO' = OM + MN + NO' = 8\) \( \Rightarrow 11 = 8 + MN \Leftrightarrow MN = 3cm.\) Chọn B. Câu 12: Phương pháp: Áp dụng tính chất của tứ giác nội tiếp. Cách giải:
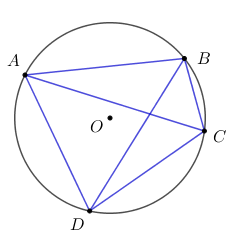
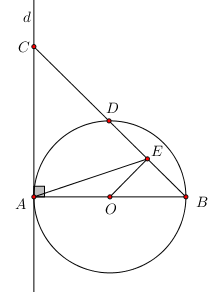
Tứ giác ABCD nội tiếp đường tròn (O) ta có: \(\widehat {ABC} + \widehat {ADC} = {180^0}\) (hai góc đối diện của tứ giác nội tiếp) \( \Rightarrow \) đáp án A sai. \(\widehat {ADB} = \widehat {ACB}\) (hai góc nội tiếp cùng chắn cung AB) \( \Rightarrow \) đáp án B đúng. Chọn A. II. TỰ LUẬN (7 ĐIỂM) Câu 13. Phương pháp: a) Đưa về so sánh \(\sqrt A \) và \(\sqrt B \) b) Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\). Cách giải: a) So sánh 5 và \(2\sqrt 6 \) Ta có \(\begin{array}{l}5 = \sqrt {25} \\2\sqrt 6 = \sqrt {{2^2}.6} = \sqrt {24} \end{array}\) Vì \(25 > 24 \Rightarrow \sqrt {25} > \sqrt {24} \Leftrightarrow 5 > 2\sqrt 6 \) b) Giải phương trình \({x^4} - 4{x^2} - 5 = 0\) Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), khi đó phương trình trở thành \(\begin{array}{l}{t^2} - 4t - 5 = 0 \Leftrightarrow {t^2} - 5t + t - 5 = 0\\ \Leftrightarrow t\left( {t - 5} \right) + \left( {t - 5} \right) = 0 \Leftrightarrow \left( {t - 5} \right)\left( {t + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 5\,\,\left( {tm} \right)\\t = - 1\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Khi \(t = 5 \Leftrightarrow {x^2} = 5 \Leftrightarrow x = \pm \sqrt 5 \). Vậy tập nghiệm của phương trình là \(S = \left\{ { \pm \sqrt 5 } \right\}\). Câu 14. Phương pháp: a) Phương trình có nghiệm kép \( \Leftrightarrow \Delta ' = 0\) b) Tìm điều kiện để phương trình có nghiệm \(\Delta ' \ge 0\), sau đó áp dụng hệ thức Vi-et \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\) Cách giải: a) Với giá trị nào của m thì phương trình có nghiệm kép? Ta có \(\Delta ' = {\left( {m + 1} \right)^2} - 4{m^2} = - 3{m^2} + 2m + 1\) Để phương trình có nghiệm kép \( \Leftrightarrow \Delta ' = 0 \Leftrightarrow - 3{m^2} + 2m + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - \dfrac{1}{3}\end{array} \right.\) b) Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình. Để phương trình có nghiệm \( \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow - \dfrac{1}{3} \le x \le 1\). Theo hệ thức Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{m + 1}}{2}\\{x_1}{x_2} = \dfrac{{{m^2}}}{4}\end{array} \right.\) Khi đó tổng bình phương các nghiệm của phương trình là : \(S = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = \dfrac{{{{\left( {m + 1} \right)}^2}}}{4} - \dfrac{{2{m^2}}}{4} = \dfrac{{ - {m^2} + 2m + 1}}{4}\) Trong trường hợp phương trình có nghiệm kép thì \(m = 1\) hoặc \(m = - \dfrac{1}{3}\), khi đó ta có \(S = \dfrac{1}{2}\) hoặc \(S = \dfrac{1}{{18}}\). Câu 15. Phương pháp: +) Gọi thời gian vòi thứ nhất chảy 1 mình đầy bể là x (h) (ĐK: \(x > 0\)) Gọi thời gian vòi thứ hai chảy 1 mình đầy bể là y (h) (ĐK: \(y > 0\)) +) Tính trong 1h mỗi vòi chảy được bao nhiêu phần của bể. +) Dựa vào các dữ kiện đã cho lập hệ phương trình và giải hệ phương trình. Cách giải: Gọi thời gian vòi thứ nhất chảy 1 mình đầy bể là x (h) (ĐK: \(x > 0\)) Gọi thời gian vòi thứ hai chảy 1 mình đầy bể là y (h) (ĐK: \(y > 0\)) Khi đó mỗi giờ vòi thứ nhất chảy được \(\dfrac{1}{x}\) bể và vòi thứ hai chảy được \(\dfrac{1}{y}\) bể. Vì nếu mở cả hai vòi nước chảy vào một bể cạn thì sau 3 giờ bể đầy nên mỗi giờ cả hai vòi chảy được \(\dfrac{1}{3}\) bể, do đó ta có phương trình \(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{3}\,\,\left( 1 \right)\). Vòi thứ nhất làm đầy bể nhanh hơn vòi thứ hai là 2 giờ 30 phút = \(\dfrac{5}{3}\,\left( h \right)\) nên ta có phương trình \(x + \dfrac{5}{2} = y\,\,\left( 2 \right)\) Thay (2) vào (1) ta có \(\dfrac{1}{x} + \dfrac{1}{{x + \dfrac{5}{2}}} = \dfrac{1}{3} \Leftrightarrow 3\left( {x + \dfrac{5}{2}} \right) + 3x = x\left( {x + \dfrac{5}{2}} \right)\) \(\begin{array}{l} \Leftrightarrow 3x + \dfrac{{15}}{2} + 3x = {x^2} + \dfrac{5}{2}x\\ \Leftrightarrow {x^2} - \dfrac{7}{2}x - \dfrac{{15}}{2} = 0\\ \Leftrightarrow 2{x^2} - 7x - 15 = 0\\ \Leftrightarrow 2{x^2} - 10x + 3x - 15 = 0\\ \Leftrightarrow 2x\left( {x - 5} \right) + 3\left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {2x + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 5\,\,\left( {tm} \right)\\x = \dfrac{{ - 3}}{2}\,\,\left( {ktm} \right)\end{array} \right. \Rightarrow y = 5 + \dfrac{5}{2} = 7,5\,\,\left( {tm} \right)\end{array}\) Vậy thời gian vòi 1 chảy một mình đày bể là 5 giờ và thời gian vòi 2 chảy 1 mình đầy bể là 7,5h. Câu 16. Phương pháp: a) Chứng minh tứ giác OACE là tứ giác có tổng hai góc đối bằng 1800. b) Chứng minh tam giác BOE đồng dạng với tam giác BCA. c) Chứng minh I di chuyển trên trung trực của OA. Cách giải: a) Chứng minh OACE là tứ giác nội tiếp. Vì E là trung điểm của BD \( \Rightarrow OE \bot BD\) (quan hệ vuông góc giữa đường kính và dây cung). Xét tứ giác OACE có \(\widehat {OAC} + \widehat {OEC} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác OACE là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800). b) Chứng minh rằng \(BE.BC = 2{R^2}\) Xét tam giác BOE và tam giác BCA có: \(\widehat {ABC}\) chung; \(\widehat {OEB} = \widehat {BAC} = {90^0}\); c) Chứng minh I di chuyển trên trung trực của OA. Ta có tứ giác OACE nội tiếp \( \Rightarrow \) Đường tròn ngoại tiếp tam giác ACE chính là đường tròn ngoại tiếp tứ giác OACE. \( \Rightarrow \) Tâm I thuộc đường trung trực của OA. Mà OA cố định \( \Rightarrow \) Trung trực của OA cố định. Vậy khi C di chuyển trên đường thẳng d thì tâm I của đường tròn ngoại tiếp tam giác ACE di chuyển trên trung trực của OA.
|














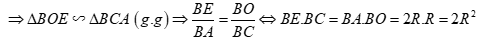






Danh sách bình luận