Đề thi vào 10 môn Toán Nghệ An năm 2021

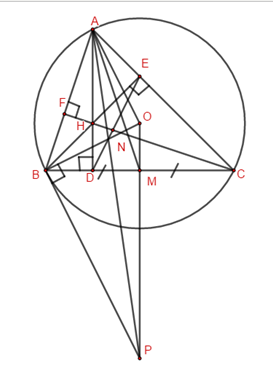
Đề bài

Câu 1 (2,5 điểm):

a) Tính \(A = \sqrt {64}  + \sqrt {16}  - 2\sqrt {36} \)

b) Xác định các hệ số \(a,\,\,b\) của đường thẳng \(y = ax + b\), biết đường thẳng này đi qua điểm \(M\left( {1;9} \right)\) và song song với đường thẳng \(y = 3x\).

c) Rút gọn biểu thức \(P = \left( {\dfrac{1}{{\sqrt x }} - \dfrac{2}{{1 + \sqrt x }}} \right).\dfrac{{x + \sqrt x }}{{1 - \sqrt x }}\), với \(x > 0,\,\,x \ne 1\).

Câu 2 (2,0 điểm)

a) Giải phương trình \(2{x^2} - 5x + 2 = 0\).

b) Cho phương trình \({x^2} - 12x + 4 = 0\) có hai nghiệm dương phân biệt \({x_1},\,\,{x_2}\). Không giải phương trình, hãy tính giá trị của biểu thức \(T = \dfrac{{x_1^2 + x_2^2}}{{\sqrt {{x_1}}  + \sqrt {{x_2}} }}\).

Câu 3 (1,5 điểm)

Vào tháng 5 năm 2021, chỉ sau 26 giờ phát hành sản phẩm âm nhạc MV “Trốn tìm” của rapper Đen Vâu đã chính thức dành Top 1 trending của YouTube Việt Nam. Giả sử trong tất cả những người đã xem MV, có 60% số người đã xem 2 lượt và những người còn lại mới chỉ xem 1 lượt. Hỏi đến thời điểm nói trên có bao nhiêu người đã xem MV, biết rằng tổng số lượt xem là 6,4 triệu lượt?

Câu 4 (3,0 điểm)

 Cho tam giác nhọn \(ABC\,\,\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\), các đường cao \(AD,\,\,BE\) và \(CF\) (\(D \in BC\), \(E \in AC\) và \(F \in AB\)) cắt nhau  tại \(H\).

a) Chứng minh \(BCEF\) là tứ giác nội tiếp.

b) Gọi \(N\) là giao điểm của \(CF\) và \(DE\). Chứng minh rằng \(DN.EF = HF.CN.\)

 c) Gọi \(M\) là trung điểm của \(BC\), tiếp tuyến tại \(B\) của đường tròn \(\left( O \right)\) cắt đường thẳng \(OM\) tại \(P\). Chứng minh \(\angle OAM = \angle DAP\).

Câu 5 (1,0 điểm)

 Giải hệ phương trình \(\left\{ \begin{array}{l}x - 3y + 2\sqrt {xy}  = 4\left( {\sqrt x  - \sqrt y } \right)\\\left( {x + 1} \right)\left( {y + \sqrt {xy}  - {x^2} + x} \right) = 4\end{array} \right.\) (\(x,y \in \mathbb{R}\)). 

Lời giải chi tiết

Câu 1

Phương pháp:

a) Vận dụng hằng đẳng thức \(\sqrt {{A^2}}  = \left| A \right|\) để rút gọn biểu thức

b) Vận dụng tính chất của hai đường thẳng song song xác định hệ số \(a\) và điều kiện của hệ số \(b\)

Đường thẳng đi qua \(M\left( {1;9} \right)\), xác định được hế số \(b\) đối chiếu điều kiện, kết luận.

c) Áp dụng quy tắc trừ, nhân các phân thức đại số để rút gọn biểu thức.

Cách giải:

a) Ta có:

\(\begin{array}{l}A = \sqrt {64}  + \sqrt {16}  - 2\sqrt {36} \\\,\,\,\,\, = 8 + 4 - 2.6 = 0\end{array}\)

Vậy \(A = 0\).

b) Ta có: \(M\left( {1;9} \right)\) thuộc đường thẳng có phương trình \(y = ax + b\) nên ta có: \(a + b = 9\,\,\left( 1 \right)\)

Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = 3x\) nên \(\left\{ \begin{array}{l}a = 3\\b \ne 0\end{array} \right.\).

Thay \(a = 3\) vào \(\left( 1 \right)\) ta được: \(b = 6\,\,\left( {tm} \right)\)

Vậy \(a = 3,\,\,b = 6\).

c) Với \(x > 0,\,\,x \ne 1\) ta có:

\(P = \left( {\dfrac{1}{{\sqrt x }} - \dfrac{2}{{1 + \sqrt x }}} \right).\dfrac{{x + \sqrt x }}{{1 - \sqrt x }}\)

    \(\begin{array}{l} = \dfrac{{1 + \sqrt x  - 2\sqrt x }}{{\sqrt x \left( {1 + \sqrt x } \right)}}.\dfrac{{\sqrt x \left( {1 + \sqrt x } \right)}}{{1 - \sqrt x }}\\ = \dfrac{{1 - \sqrt x }}{{1 - \sqrt x }} = 1\end{array}\)

Vậy \(P = 1\) với \(x > 0,\,\,x \ne 1\).

Câu 2

Phương pháp:

a) Vận dụng công thức nghiệm của phương trình bậc hai một ẩn, xác định nghiệm của hệ phương trình.

b) Áp dụng hệ thức Vi – ét, xác định \({x_1} + {x_2};{x_1}{x_2}\) để tính giá trị của biểu thức \(T\)

Chú ý: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\); \({\left( {\sqrt {{x_1}}  + \sqrt {{x_2}} } \right)^2} = {x_1} + {x_2} + 2\sqrt {{x_1}{x_2}}  \Rightarrow \sqrt {{x_1}}  + \sqrt {{x_2}} \)

Cách giải:

a) Ta có: \(\Delta  = {5^2} - 4.2.2 = 9 > 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - b + \sqrt \Delta  }}{{2a}} = \dfrac{{5 + \sqrt 9 }}{{2.2}} = 2\\{x_1} = \dfrac{{ - b - \sqrt \Delta  }}{{2a}} = \dfrac{{5 - \sqrt 9 }}{{2.2}} = \dfrac{1}{2}\end{array} \right.\).

Vậy tập nghiệm của phương trình là \(S = \left\{ {2;\dfrac{1}{2}} \right\}\).

b) Vì phương trình \({x^2} - 12x + 4 = 0\) có hai nghiệm dương phân biệt \({x_1},\,\,{x_2}\) nên theo định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 12\\{x_1}{x_2} = 4\end{array} \right.\).

Ta có:

\(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {12^2} - 2.4 = 136\)

\({\left( {\sqrt {{x_1}}  + \sqrt {{x_2}} } \right)^2} = {x_1} + {x_2} + 2\sqrt {{x_1}{x_2}}  = 12 + 2\sqrt 4  = 16 \Rightarrow \sqrt {{x_1}}  + \sqrt {{x_2}}  = 4\).

Vậy \(T = \dfrac{{x_1^2 + x_2^2}}{{\sqrt {{x_1}}  + \sqrt {{x_2}} }} = \dfrac{{136}}{4} = 34\).

Câu 3  

Phương pháp:

Gọi \(x\) là số người đã xem MV (triệu người)

Xác định số người đã xem 2 lượt và số người chỉ xem 1 lượt

Theo giả thiết, tổng số lượt xem là 6,4 triệu nên lập phương trình

Giải phương trình, xác định \(x\), đối chiếu điều kiện, kết luận.

Cách giải:

Gọi \(x\) là số người đã xem MV (triệu người) \(\left( {x \in {\mathbb{N}^*}} \right)\)

Khi đó số người đã xem 2 lượt là \(60\% x = 0,6x\) (người) và số người chỉ xem 1 lượt là \(40\% x = 0,4x\) (người).

Vì tổng số lượt xem là 6,4 triệu nên ta có phương trình:

\(\begin{array}{l}0,6x.2 + 0,4x.1 = 1,6x = 6,4\\ \Leftrightarrow 1,6x = 6,4 \Leftrightarrow x = 4\end{array}\)

Vậy có 4 triệu người xem MV.

Câu 4

Phương pháp:

a) Vận dụng dấu hiệu nhận của tứ giác: tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau.

b) Vận dụng tính chất của tam giác đồng dạng, tính chất đường phân giác.

c) Áp dụng kiến thức góc – đường tròn, tiếp tuyến của đường tròn và tam giác đồng dạng.

Cách giải:

a) Ta có \(\angle BEC = \angle BFC = {90^0}\) (do \(BE \bot AC,\,\,CF \bot AB\))

\( \Rightarrow BCEF\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).

b) Ta có \(\angle CDH = \angle CEH = {90^0}\,\,\left( {gt} \right) \Rightarrow \angle CDH + \angle CEH = {180^0}\) nên \(CDHE\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).

\( \Rightarrow \angle DCN = \angle NEH\)(Hai góc nội tiếp cùng chắn cung \(DH\)).

Xét tam giác \(\Delta DCN\) và \(\Delta HEN\) ta có:

\(\angle DCN = \angle NEH\,\,\left( {cmt} \right)\)

\(\angle DNC = \angle HNE\) (đối đỉnh)

\( \Rightarrow \Delta DCN\) đồng dạng với \(\Delta HEN\) (g.g)

\( \Rightarrow \dfrac{{DN}}{{NC}} = \dfrac{{HN}}{{EN}}\) (hai cạnh tương ứng)         (1)

Ta có \(BCEF\) là tứ giác nội tiếp (cmt) nên \(\angle DCN = \angle HEF\) (2 góc nội tiếp cùng chắn cung \(BF\)).

Mà \(\angle DCN = \angle NEH\,\,\left( {cmt} \right)\) nên \(\angle NEH = \angle HEF\) hay \(EH\) là tia phân giác của \(\angle NEF\).

\( \Rightarrow \dfrac{{HN}}{{EN}} = \dfrac{{HF}}{{EF}}\) (tính chất đường phân giác)         (2)

Từ (1) và (2) ta được \(\dfrac{{DN}}{{NC}} = \dfrac{{HF}}{{EF}} \Leftrightarrow DN.EF = HF.CN\) (đpcm)

c) Ta có \(M\) là trung điểm của \(BC\) nên \(OM \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung).

Mà \(BC \bot AD\,\,\left( {gt} \right)\) nên \(OM//AD \Rightarrow OP//AD\)

\( \Rightarrow \angle DAP = \angle APO\) (so le trong)          (3)

Mặt khác ta có: \(PB\) là tiếp tuyến của \(\left( O \right)\) tại \(B\) nên \(OB \bot BP \Rightarrow \angle OBP = {90^0}\) (định nghĩa).

Áp dụng hệ thức lượng tròn tam giác \(OPB\) vuông tại \(B\) có \(BM\) là đường cao ta có \(O{B^2} = OM.OP\).

Mà  \(O{A^2} = O{B^2} \Rightarrow O{A^2} = OM.OP \Rightarrow \dfrac{{OM}}{{OA}} = \dfrac{{OA}}{{OP}}\).

Xét tam giác \(\Delta OAM\) và \(\Delta OPA\) ta có:

\(\angle AOP\) chung;

\(\dfrac{{OM}}{{OA}} = \dfrac{{OA}}{{OP}}\,\,\left( {cmt} \right);\)

\( \Rightarrow \Delta OAM\) đồng dạng với \(\Delta OPA\) (c.g.c)

\( \Rightarrow \angle OAM = \angle OPA\) (2 góc tương ứng)            (4)

Từ (3) và (4) suy ra \(\angle OAM = \angle DAP\) (đpcm)

Câu 5

Phương pháp:

Xác định điều kiện của hệ phương trình

Đặt \(\left\{ \begin{array}{l}x - 3y + 2\sqrt {xy}  = 4\left( {\sqrt x  - \sqrt y } \right)\,\,\,\left( 1 \right)\\\left( {x + 1} \right)\left( {y + \sqrt {xy}  - {x^2} + x} \right) = 4\,\,\,\,\left( 2 \right)\end{array} \right.\), biến đổi phương trình (1), tìm được mối liên hệ giữa \(x\) và \(y\)

Thế lần lượt vào phương trình (2), tìm nghiệm của hệ phương trình, đối chiếu điều kiện, kết luận.

Cách giải:

ĐKXĐ: \(x,\,\,y \ge 0\).

\(\left\{ \begin{array}{l}x - 3y + 2\sqrt {xy}  = 4\left( {\sqrt x  - \sqrt y } \right)\,\,\,\left( 1 \right)\\\left( {x + 1} \right)\left( {y + \sqrt {xy}  - {x^2} + x} \right) = 4\,\,\,\,\left( 2 \right)\end{array} \right.\)

\(\begin{array}{l}\left( 1 \right) \Leftrightarrow x - \sqrt {xy}  + 3\sqrt {xy}  - 3y = 4\left( {\sqrt x  - \sqrt y } \right)\\\,\,\,\,\,\,\, \Leftrightarrow \sqrt x \left( {\sqrt x  - \sqrt y } \right) + 3\sqrt y \left( {\sqrt x  - \sqrt y } \right) = 4\left( {\sqrt x  - \sqrt y } \right)\\\,\,\,\,\,\,\, \Leftrightarrow \left( {\sqrt x  - \sqrt y } \right)\left( {\sqrt x  + 3\sqrt y } \right) = 4\left( {\sqrt x  - \sqrt y } \right)\\\,\,\,\,\,\,\, \Leftrightarrow \left( {\sqrt x  - \sqrt y } \right)\left( {\sqrt x  + 3\sqrt y  - 4} \right) = 0\\\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}\sqrt x  = \sqrt y \\\sqrt x  + 3\sqrt y  = 4\end{array} \right.\end{array}\)

TH1: \(\sqrt x  = \sqrt y \) \( \Leftrightarrow x = y\). Thay vào (2) ta có:

\(\begin{array}{l}\left( {x + 1} \right)\left( {x + x - {x^2} + x} \right) = 4\\ \Leftrightarrow \left( {x + 1} \right)\left( {3x - {x^2}} \right) = 4\\ \Leftrightarrow {x^3} - 2{x^2} - 3x + 4 = 0\\ \Leftrightarrow {x^3} - 1 - \left( {2{x^2} + 3x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + x + 1} \right) - \left( {x - 1} \right)\left( {2x + 5} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + x + 1 - 2x - 5} \right) = 0\end{array}\)

\(\begin{array}{l} \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1 = y\\x = \dfrac{{1 + \sqrt {17} }}{2} = y\,\,\left( {do\,\,x,y \ge 0} \right)\end{array} \right.\end{array}\)

TH2: \(\left\{ \begin{array}{l}\sqrt x  + 3\sqrt y  = 4\\\left( {x + 1} \right)\left( {y + \sqrt {xy}  - {x^2} + x} \right) = 4\end{array} \right.\).

Đặt \(\sqrt x  = a,\,\,\sqrt y  = b\,\,\left( {a,b \ge 0} \right)\) \( \Rightarrow \left\{ \begin{array}{l}a + 3b = 4 \Leftrightarrow b = \dfrac{{4 - a}}{3}\\\left( {{a^2} + 1} \right)\left( {{b^2} + ab - {a^4} + {a^2}} \right) = 4\,\,\left( * \right)\end{array} \right.\)

Thế \(b = \dfrac{{4 - a}}{3}\) vào (*) ta được:

\(\begin{array}{l}\left( {{a^2} + 1} \right)\left( {{{\left( {\dfrac{{4 - a}}{3}} \right)}^2} + a.\dfrac{{4 - a}}{3} - {a^4} + {a^2}} \right) = 4\\ \Leftrightarrow \left( {{a^2} + 1} \right).\dfrac{{16 - 8a + {a^2} + 12a - 3{a^2} - 9{a^4} + 9{a^2}}}{9} = 4\\ \Leftrightarrow \left( {{a^2} + 1} \right)\left( { - 9{a^4} + 7{a^2} + 4a + 16} \right) = 32\\ \Leftrightarrow 9{a^6} + 2{a^4} - 4{a^3} - 23{a^2} - 4a + 20 = 0\\ \Leftrightarrow {\left( {a - 1} \right)^2}\left( {9{a^4} + 18{a^3} + 29{a^2} + 36a + 20} \right) = 0\\ \Leftrightarrow a = 1\,\,\left( {do\,\,a \ge 0} \right) \Rightarrow b = \dfrac{{4 - 1}}{3} = 1\\ \Rightarrow \left\{ \begin{array}{l}\sqrt x  = 1 \Leftrightarrow x = 1\\\sqrt y  = 1 \Leftrightarrow y = 1\end{array} \right.\end{array}\)

Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) \in \left\{ {\left( {1;1} \right);\left( {\dfrac{{1 + \sqrt {17} }}{2};\dfrac{{1 + \sqrt {17} }}{2}} \right)} \right\}\).