Đề thi vào 10 môn Toán Nghệ An năm 2018Tải vềCâu 1 (2,5 điểm): a) So sánh Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài Câu 1 (2,5 điểm): a) So sánh \(2\sqrt 3 + \sqrt {27} \) và \(\sqrt {74} .\) b) Chứng minh đẳng thức: \(\left( {\dfrac{1}{{\sqrt x - 2}} - \dfrac{1}{{\sqrt x + 2}}} \right).\dfrac{{x - 4}}{4} = 1,\) với \(x \ge 0\) và \(x \ne 4.\) c) Tìm giá trị của \(m\) để đồ thị hàm số \(y = 3x + m\) đi qua điểm \(A\left( {1;\;2} \right).\) Câu 2 (2 điểm): Cho phương trình \({x^2} + 2x + m - 1 = 0\;\;\;\;\left( * \right),\) trong đó \(m\) là tham số. a) Giải phương trình \(\left( * \right)\) khi \(m = - 2.\) b) Tìm \(m\) để phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn điều kiện \({x_1} = 2{x_2}.\) Câu 3 (1,5 điểm): Nhân ngày sách Việt Nam, 120 học sinh khối 8 và 100 học sinh khối 9 cùng tham gia phong trào xây dựng “Tủ sách nhân ái”. Sau một thời gian phát động, tổng số sách cả hai khối đã quyên góp được là 540 quyển. Biết rằng mỗi học sinh khối 9 quyên góp nhiều hơn nhiều hơn mỗi học sinh khối 8 một quyển. Hỏi mỗi khối đã quyên góp được bao nhiêu quyển sách? (Mỗi học sinh trong cùng một khối quyên góp số lượng sách như nhau). Câu 4 (3 điểm): Cho đường tròn (O) có dây BC cố định không đi qua tâm O. Điểm A di động trên (O) sao cho tam giác ABC có 3 góc nhọn. Các đường cao BE, CF của tam giác ABC (E thuộc AC, F thuộc AB) cắt nhau tại H. Gọi K là giao điểm của hai đường thẳng EF và BC, đoạn thẳng KA cắt (O) tại điểm M. Chứng minh rằng: a) BCEF là tứ giác nội tiếp. b) KM.KA = KE.KF. c) Đường thẳng MH luôn đi qua một điểm cố định khi A thay đổi. Câu 5 (1 điểm): Giải hệ phương trình: \(\left\{ \begin{array}{l}x\left( {2x - 2y + 1} \right) = y\\y + 2\sqrt {1 - x - 2{x^2}} = 2\left( {1 + {y^2}} \right)\end{array} \right..\) Lời giải chi tiết
Phương pháp: a) Rút gọn số hạng thứ nhất sau đó so sánh theo tính chất: với mọi \(a > b > 0\) ta có: \(\sqrt a > \sqrt b .\) b) Quy đồng mẫu các phân thức và rút gọn biểu thức ở vế trái sao cho bằng biểu thức ở vế phải. c) Thay tọa độ điểm A vào công thức hàm số đểm tìm m. Cách giải: a) So sánh \(2\sqrt 3 + \sqrt {27} \) và \(\sqrt {74} .\) Ta có: \(2\sqrt 3 + \sqrt {27} = 2\sqrt 3 + 3\sqrt 3 = 5\sqrt 3 = \sqrt {{5^2}.3} = \sqrt {75} .\) Vì \(75 > 74 \Rightarrow \sqrt {75} > \sqrt {74} \Rightarrow 2\sqrt 3 + \sqrt {27} > \sqrt {74} .\) Vậy \(2\sqrt 3 + \sqrt {27} > \sqrt {74} .\) b) Chứng minh đẳng thức: \(\left( {\dfrac{1}{{\sqrt x - 2}} - \dfrac{1}{{\sqrt x + 2}}} \right).\dfrac{{x - 4}}{4} = 1,\) với \(x \ge 0\) và \(x \ne 4.\) \(\begin{array}{l}\;\;\;\left( {\dfrac{1}{{\sqrt x - 2}} - \dfrac{1}{{\sqrt x + 2}}} \right).\dfrac{{x - 4}}{4}\\ = \dfrac{{\sqrt x + 2 - \sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}.\dfrac{{x - 4}}{4}\\ = \dfrac{4}{{x - 4}}.\dfrac{{x - 4}}{4} = 1\;\;\;\left( {dpcm} \right).\end{array}\) Vậy với \(x \ge 0,\;x \ne 4\) ta có: \(\left( {\dfrac{1}{{\sqrt x - 2}} - \dfrac{1}{{\sqrt x + 2}}} \right).\dfrac{{x - 4}}{4} = 1.\) c) Tìm giá trị của \(m\) để đồ thị hàm số \(y = 3x + m\) đi qua điểm \(A\left( {1;\;2} \right).\) Đồ thị hàm số đi qua điểm \(A\left( {1;\;2} \right) \Rightarrow 2 = 3.1 + m \Leftrightarrow m = - 1.\) Vậy \(m = - 1.\)
Phương pháp: a) Thay giá trị \(m = - 2\) vào phương trình sau đó giải phương trình bậc hai một ẩn. b) Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\) +) Áp dụng hệ thức Vi-ét \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\) và biểu thức bài cho để tìm \(m.\) Cách giải: a) Giải phương trình \(\left( * \right)\) khi \(m = - 2.\) Với \(m = - 2\) ta có phương trình \(\begin{array}{l}\left( * \right) \Leftrightarrow {x^2} + 2x - 3 = 0\\ \Leftrightarrow {x^2} + 3x - x - 3 = 0\\ \Leftrightarrow x\left( {x + 3} \right) - \left( {x + 3} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right..\end{array}\) Vậy với \(m = - 2\) thì phương trình có tập nghiệm \(S = \left\{ { - 3;\;1} \right\}.\) b) Tìm \(m\) để phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn điều kiện \({x_1} = 2{x_2}.\) Phương trình có hai nghiệm phân biệt \({x_1},\;\;{x_2} \Leftrightarrow \Delta ' > 0\) \( \Leftrightarrow 1 - m + 1 > 0 \Leftrightarrow m < 2.\) Với \(m < 2\) thì phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1},\;{x_2}.\) Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\;\;\left( 1 \right)\\{x_1}{x_2} = m - 1\;\;\;\left( 2 \right)\end{array} \right..\) Theo đề bài ta có: \({x_1} = 2{x_2}.\) Kết hợp với phương trình (1) ta có hệ phương trình: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1} = 2{x_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1} - 2{x_2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = - \dfrac{4}{3}\\{x_2} = - \dfrac{2}{3}\end{array} \right..\) \( \Rightarrow \left( 2 \right) \Leftrightarrow {x_1}{x_2} = m - 1 \Leftrightarrow \left( { - \dfrac{2}{3}} \right).\left( { - \dfrac{4}{3}} \right) = m - 1 \Leftrightarrow m = \dfrac{{17}}{9}\;\;\left( {tm} \right).\) Vậy \(m = \dfrac{{17}}{9}\) thỏa mãn bài toán.
Phương pháp: Gọi số sách khối 8 và khối 9 quyên góp được lần lượt là \(x,\;y\) (quyển sách), \(\left( {0 < x,\;y < 540,\;x,\;y \in N} \right).\) Dựa vào giả thiết của bài toán để lập hệ phương trình và giải hệ phương trình. +) Phương trình thứ nhất: Số sách lớp 8 + số sách lớp 9 quyên góp được = 540. +) Phương trình thứ hai: Số sách mỗi học sinh khối 9 – số sách mỗi học sinh khối 8 = 1. Giải hệ phương trình vừa lập để tìm \(x,\;y\) và kết luận. Cách giải: Gọi số sách khối 8 và khối 9 quyên góp được lần lượt là \(x,\;y\) (quyển sách), \(\left( {0 < x,\;y < 540,\;x,\;y \in N} \right).\) Số sách cả hai khối quyên góp được là: \(x + y = 540\;\;\;\;\left( 1 \right).\) Số sách một bạn học sinh khối 8 quyên góp là: \(\dfrac{x}{{120}}\) (quyển) Số sách một bạn học sinh khối 9 quyên góp là: \(\dfrac{y}{{100}}\) (quyển) Mỗi học sinh khối 9 quyên góp nhiều hơn nhiều hơn mỗi học sinh khối 8 một quyển nên ta có phương trình: \(\dfrac{y}{{100}} - \dfrac{x}{{120}} = 1 \Leftrightarrow - 5x + 6y = 600\;\;\;\left( 2 \right).\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 540\\ - 5x + 6y = 600\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x + 5y = 2700\\ - 5x + 6y = 600\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}11y = 3300\\x = 540 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 300\;\;\left( {tm} \right)\\x = 240\;\;\left( {tm} \right)\end{array} \right..\) Vậy khối 9 đã quyên góp được 300 quyển sách, khối 8 đã quyên góp được 240 quyển sách.
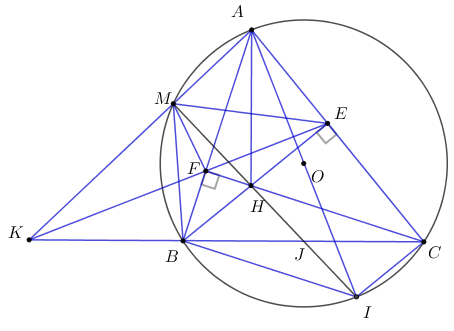
Phương pháp: a) Chứng minh tứ giác BCEF có hai đỉnh E và F cùng nhìn BC dưới 1 góc bằng nhau. b) Chứng minh tam giác MKB và tam giác CKA đồng dạng, chứng minh tam giác KBF và tam giác KEC đồng dạng. c) Kéo dài MH cắt (O) tại I. chứng minh AI là đường kính của đường tròn (O). Chứng minh BICH là hình bình hành, suy ra MH đi qua trung điểm của BC cố định. Cách giải:
a) BCEF là tứ giác nội tiếp. Xét tứ giác \(BFEC\) ta có: \(\widehat {BFC} = \widehat {BEC} = {90^0}\) Mà hai đỉnh này cùng kề một cạnh và cùng nhìn cạnh \(BC\) dưới hai góc bằng nhau. \( \Rightarrow BCEF\) là tứ giác nội tiếp. (dhnb) b) KM.KA = KE.KF. Vì \(BMAC\) là tứ giác nội tiếp \( \Rightarrow \widehat {KMB} = \widehat {ACB}\) (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện). Xét \(\Delta MKB\) và \(\Delta CKA\) ta có: \(\begin{array}{l}\widehat {AKC}\;\;chung\\\widehat {KMB} = \widehat {ACK}\;\;\left( {cmt} \right)\\ \Rightarrow \Delta MKB \sim \Delta CKA\;\left( {g - g} \right).\\ \Rightarrow \dfrac{{MK}}{{CK}} = \dfrac{{KB}}{{KA}} \Leftrightarrow KM.KA = KC.KB\;\;\;\;\left( 1 \right).\end{array}\) Vì tứ giác \(BCEF\) là tứ giác nội tiếp \( \Rightarrow \widehat {KBF} = \widehat {FEC}\) (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện). Xét \(\Delta KBF\) và \(\Delta KEC\) ta có: \(\begin{array}{l}\widehat {CKF}\;\;chung\\\widehat {KBF} = \widehat {KEC}\;\;\left( {cmt} \right)\\ \Rightarrow \Delta KBF \sim \Delta KEC\;\left( {g - g} \right).\\ \Rightarrow \dfrac{{KB}}{{KE}} = \dfrac{{KF}}{{KC}} \Leftrightarrow KB.KC = KF.KF\;\;\;\;\left( 2 \right).\end{array}\) Từ (1) và (2) ta có: \(KM.KA = KE.KF\left( { = KB.KC} \right).\;\;\;\left( {dpcm} \right)\) c) Đường thẳng MH luôn đi qua một điểm cố định khi A thay đổi. Kéo dài \(MH\) cắt đường tròn tại \(I.\) Ta có: \(KM.KA = KE.KF\left( {cmt} \right) \Rightarrow \dfrac{{KM}}{{KF}} = \dfrac{{KE}}{{KA}}.\) Xét \(\Delta KME\) và \(\Delta KFA\) ta có: \(\begin{array}{l}\dfrac{{KM}}{{KF}} = \dfrac{{KE}}{{KA}}\;\;\left( {cmt} \right)\\\widehat {AKE}\;\;chung.\\ \Rightarrow \Delta KME \sim \Delta KFA\;\left( {c.g.c} \right).\\ \Rightarrow \widehat {KAF} = \widehat {KEM}\;\;hay\;\;\widehat {MEF} = \widehat {MAF}.\end{array}\) Mà hai góc này là hai góc kề một cạnh và cùng nhìn cạnh \(MF\) dưới hai góc bằng nhau. \( \Rightarrow MAEF\) là tứ giác nội tiếp hay \(M,\;A,\;E,\;F\) cùng thuộc một đường tròn. (dhnb) Xét tứ giác \(AEHF\) ta có: \(\widehat {AFH} + \widehat {AEH} = {90^0} + {90^0} = {180^0}.\) \( \Rightarrow AEHF\) là tứ giác nội tiếp hay \(A,\;E,\;H,\;F\) cùng thuộc một đường tròn. \( \Rightarrow A,\;M,\;F,\;H,\;E\) cùng thuộc một đường tròn. Lại có \(\widehat {AFH} = \widehat {AEH} = {90^0} \Rightarrow AH\) đường kính của đường tròn đi qua 5 điểm \(A,\;M,\;F,\;H,\;E.\) Mặt khác, \(\widehat {AMH}\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {AMH} = {90^0}\;\;hay\;\;\widehat {AMI} = {90^0} \Rightarrow AI\) là đường kính của đường tròn \(\left( O \right).\) \(\begin{array}{l} \Rightarrow \widehat {ABI} = {90^0}\;\;hay\;\;AB \bot BI.\\ \Rightarrow BI//CF\;\;hay\;\;BC//CF\end{array}\) Chứng minh tương tự ta được \(CI//BE\;\;hay\;\;CI//BH.\) \( \Rightarrow BHCI\) là hình bình hành (dấu hiệu nhận biết) \( \Rightarrow BC \cap HI = \left\{ J \right\}\) hay \(BC \cap MH = \left\{ J \right\}\) với \(J\) là trung điểm của \(BC.\) Mà \(BC\) cố định nên \(J\) cố định. Vậy khi \(A\) thay đổi ta có \(MH\) luôn đi qua trung điểm \(J\) cố định của cạnh \(BC.\) Câu 5: Cách giải: Giải hệ phương trình: \(\left\{ \begin{array}{l}x\left( {2x - 2y + 1} \right) = y\\y + 2\sqrt {1 - x - 2{x^2}} = 2\left( {1 + {y^2}} \right)\end{array} \right..\) \(\left\{ \begin{array}{l}x\left( {2x - 2y + 1} \right) = y\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 1 \right)\\y + 2\sqrt {1 - x - 2{x^2}} = 2\left( {1 + {y^2}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 2 \right)\end{array} \right..\) Điều kiện: \(1 - x - 2{x^2} \ge 0 \Leftrightarrow \left( {x + 1} \right)\left( {2x - 1} \right) \le 0 \Leftrightarrow - 1 \le x \le \dfrac{1}{2}.\) Ta có: \(\left( 1 \right) \Leftrightarrow x\left( {2x - 2y + 1} \right) = y \Leftrightarrow 2{x^2} - 2xy + x - y = 0\) \(\begin{array}{l} \Leftrightarrow 2x\left( {x - y} \right) + \left( {x - y} \right) = 0\\ \Leftrightarrow \left( {2x + 1} \right)\left( {x - y} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 0\\x - y = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\;\;\;\;\left( {tm} \right)\\x = y\end{array} \right..\end{array}\) +) Với \(x = - \dfrac{1}{2} \Rightarrow \left( 2 \right) \Leftrightarrow y + 2\sqrt {1 + \dfrac{1}{2} - 2.\dfrac{1}{4}} = 2\left( {1 + {y^2}} \right)\) \(\begin{array}{l} \Leftrightarrow y + 2 = 2 + 2{y^2} \Leftrightarrow 2{y^2} - y = 0\\ \Leftrightarrow y\left( {2y - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}y = 0\\2y - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = 0\\y = \dfrac{1}{2}\end{array} \right..\end{array}\) Khi đó hệ có tập nghiệm \(\left( {x;\;y} \right) = \left\{ {\left( { - \dfrac{1}{2};\;0} \right),\;\;\left( { - \dfrac{1}{2};\;\dfrac{1}{2}} \right)} \right\}.\) +) Với \(x = y \Rightarrow \left( 2 \right) \Leftrightarrow x + 2\sqrt {1 - x - 2{x^2}} = 2\left( {1 + {x^2}} \right)\) \(\begin{array}{l} \Leftrightarrow 2\sqrt {1 - x - 2{x^2}} = 4{x^2} - 2{x^2} - x + 1 + 1\\ \Leftrightarrow 4{x^2} - 2{x^2} - x + 1 - 2\sqrt {1 - x - 2{x^2}} + 1 = 0\\ \Leftrightarrow 4{x^2} + {\left( {\sqrt {1 - x - 2{x^2}} - 1} \right)^2} = 0\\ \Leftrightarrow \left\{ \begin{array}{l}2x = 0\\\sqrt {1 - x - 2{x^2}} - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\1 - x - 2{x^2} = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 0\\2{x^2} + x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\\left[ \begin{array}{l}x = 0\\x = - 2\,\,\left( {ktm} \right)\end{array} \right.\end{array} \right. \Leftrightarrow x = 0\;\;\left( {tm} \right) \Rightarrow y = 0.\end{array}\) Vậy hệ phương trình có nghiệm \(\left( {x;\;y} \right) = \left\{ {\left( { - \dfrac{1}{2};\;0} \right),\;\;\left( { - \dfrac{1}{2};\;\dfrac{1}{2}} \right),\;\;\left( {0;\;0} \right)} \right\}.\)
|




















Danh sách bình luận