Đề thi vào 10 môn Toán Yên Bái năm 2023

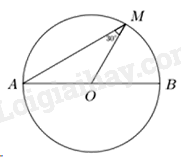
Đề bài

Câu 1: Trong các hàm số sau, hàm số nào là hàm số bậc nhất?

A. \(y = \frac{1}{{{x^2}}} + 3\).

B. \(y = 3{x^2} - 2\).

C. \(y = 3x + 2\).

D. \(y = 3{x^2} - 1\).

Câu 2: Cho tam giác ABC vuông tại \(A\), đường cao \(AH{\mkern 1mu} {\mkern 1mu} \left( {H \in BC} \right)\). Khẳng định nào sau đây đúng?

A. \(A{H^2} = BH.CH\).

B. \(A{H^2} = B{H^2}.C{H^2}\).

C. \(AH = \frac{{BH}}{{CH}}\).

D. \(AH = BH.CH\).

Câu 3: Tứ giác ABCD có số đo \(\angle A = 80^\circ ,{\mkern 1mu} {\mkern 1mu} \angle B = 110^\circ ,{\mkern 1mu} {\mkern 1mu} \angle C = 100^\circ \). Số đo \(\angle D\) bằng:

A. \(100^\circ \).

B. \(80^\circ \).

C. \(110^\circ \).

D. \(70^\circ \).

Câu 4: Hai đường tròn phân biệt có số điểm chung nhiều nhất là

A. 1.

B. 0.

C. Vô số.

D. 2.

Câu 5: Phương trình nào sau đây là phương trình bậc hai một ẩn?

A. \(2x - 3 = 0\).

B. \({x^4} - 2{x^2} = 0\).

C. \({x^3} + 3 = 0\).

D. \({x^2} - 2x - 3 = 0\).

Câu 6: Giá trị của \(\sin 30^\circ \) bằng

A. \(\frac{1}{2}\).

B. \(\frac{{\sqrt 2 }}{2}\).

C. \(\frac{{\sqrt 3 }}{2}\).

D. \(1\).

Câu 7: Cặp số \(\left( {1;2} \right)\) là nghiệm của phương trình nào sau đây?

A. \(3x - 2y = 7\).

B. \(3x + 2y = 8\).

C. \(3x + 2y = 7\).

D. \(3x - 2y = 8\).

Câu 8: Công thức tính diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi rh\). Diện tích xung quanh của hình trụ có bán kính đáy \(r = 2\), chiều cao \(h = 3\) là:

A. \({S_{xq}} = 24\pi \)(đvdt)

B. \({S_{xq}} = 12\pi \)(đvdt)

C. \({S_{xq}} = 6\pi \)(đvdt)

D. \({S_{xq}} = 48\pi \)(đvdt)

Câu 9: Đường thẳng \(y = 2x - 1\) đi qua điểm nào sau đây?

A. \(Q\left( {1; - 1} \right)\).

B. \(M\left( { - 1; - 3} \right)\).

C. \(N\left( {1;3} \right)\).

D. \(P\left( { - 3; - 5} \right)\).

Câu 10: Tập nghiệm của phương trình \({x^2} - 4x + 3 = 0\) là:

A. \(\left\{ {1;3} \right\}\).

B. \(\left\{ {1; - 3} \right\}\).

C. \(\left\{ { - 1; - 3} \right\}\).

D. \(\left\{ { - 1;3} \right\}\).

Câu 11: Ước chung lớn nhất của \(6\) và \(9\) là:

A. 9.

B. 6.

C. 3.

D. 18.

Câu 12: Cho \(\Delta ABC\) cân tại \(A\). Khẳng định nào sau đây đúng?

A. \(AB < AC\).

B. \(AB \ne AC\).

C. \(AB = AC\).

D. \(AB > AC\).

Câu 13: Hệ số góc \(a\) của đường thẳng \(y = 2x + 3\) là

A. \(a = \frac{1}{2}\).

B. \(a = 2\).

C. \(a = \frac{1}{3}\).

D. \(a = 3\).

Câu 14: Góc nội tiếp chắn nửa đường tròn là :

A. góc vuông.

B. góc tù.

C. góc nhọn.

D. góc bẹt.

Câu 15: Giá trị của biểu thức \(\sqrt 9 {\rm{ \;}} + 5\) bằng

A. 14.

B. 8.

C. 6.

D. 4.

Câu 16: Điều kiện xác định của \(\sqrt {x - 10} \) là

A. \(x < 10\).

B. \(x < {\rm{ \;}} - 10\).

C. \(x \ge 10\).

D. \(x \ne 10\).

Câu 17: Cho đường tròn \(\left( {O;12cm} \right)\). Dây lớn nhất của đường tròn có độ dài bằng

A. \(48cm\).

B. \(144cm\).

C. \(24cm\).

D. \(12cm\).

Câu 18: Kết quả của phép tính \({a^3}.{a^5}\) bằng

A. \({a^7}\).

B. \({a^9}\).

C. \({a^8}\).

D. \({a^{10}}\).

Câu 19: Phân tích đa thức \({x^2} - 5x\) thành nhân tử ta được

A. \(x\left( {5 - x} \right)\).

B. \({x^2}\left( {x - 5} \right)\).

C. \(x\left( {x + 5} \right)\).

D. \(x\left( {x - 5} \right)\).

Câu 20: Trên đường tròn \(\left( O \right)\) lấy hai điểm \(A,{\mkern 1mu} {\mkern 1mu} B\) sao cho \(\angle AOB = 60^\circ \). Số đo cung nhỏ AB là:

A. \(30^\circ \).

B. \(90^\circ \).

C. \(120^\circ \).

D. \(60^\circ \).

Câu 21: Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x - y = 5}\\{5x + 4y = 14}\end{array}} \right.\) có nghiệm là

A. \(\left( { - 2; - 1} \right)\).

B. \(\left( {2;1} \right)\).

C. \(\left( {2; - 1} \right)\).

D. \(\left( { - 2;1} \right)\).

Câu 22: Hàm số nào sau đây thỏa mãn \(f\left( 2 \right) = f\left( { - 2} \right)\)?

A. \(f\left( x \right) = \frac{{ - x + 1}}{2}\).

B. \(f\left( x \right) = \frac{x}{2} + 1\).

C. \(f\left( x \right) = {\rm{ \;}} - \frac{x}{2} + 2\).

D. \(f\left( x \right) = \frac{{{x^2}}}{2}\).

Câu 23: Giá trị của tham số \(m\) để đồ thị hàm số \(y = \left( {m - 2} \right){x^2}\) đi qua điểm \(P\left( {1; - 1} \right)\) là

A. \(m = {\rm{ \;}} - 1\).

B. \(m = 1\).

C. \(m = 3\).

D. \(m = {\rm{ \;}} - 3\).

Câu 24: Cho phương trình \({x^2} - 3x + 2 = 0\). Tích các nghiệm của phương trình là:

A. \( - 2\).

B. \( - 3\).

C. \(3\).

D. \(2\).

Câu 25: Cho đường tròn \(\left( {O;15cm} \right)\), dây \(AB = 24cm\). Khoảng cách từ \(O\) đến dây AB là

A. \(8cm\).

B. \(9cm\).

C. \(12cm\).

D. \(10cm\).

Câu 26: Thể tích hình nón có chiều cao \(h = 2cm\) và bán kính đáy \(r = 3cm\) là

A. \(V = 8\pi c{m^3}\).

B. \(V = 12\pi c{m^3}\).

C. \(V = 6\pi c{m^3}\).

D. \(V = 4\pi c{m^3}\).

Câu 27: Cho đường tròn \(\left( O \right)\) có diện tích bằng \(64\pi c{m^2}\). Chu vi của đường tròn là

A. 8cm

B. \(8\pi cm\)

C. 16cm

D. \(16\pi cm\)

Câu 28: Khẳng định nào sau đây đúng?

A. \(\sin 25^\circ  = \tan 65^\circ \).

B. \(\sin 25^\circ  = \cos 75^\circ \).

C. \(\sin 25^\circ  = \cos 65^\circ \).

D. \(\sin 25^\circ  = \cot 65^\circ \).

Câu 29: Cho \(a < 0\). Kết quả rút gọn biểu thức \(P = \frac{{\sqrt {{a^2}} }}{2} + \frac{{3a}}{2}\) là

A. 4a.

B. \(\frac{{3a}}{2}\).

C. 2a.

D. \(a\).

Câu 30: Tích các nghiệm của phương trình \(\left( {x - 1} \right)\left( {{x^2} - 4} \right) = 0\) là

A. \( - 4\).

B. \(2\).

C. \(4\).

D. \( - 2\).

Câu 31: Biết \(\frac{x}{y} = \frac{3}{2}\) và \(2x - y = 8\). Khi đó giá trị của \(y\) là

A. \( - 6\).

B. \(6\).

C. \( - 4\).

D. \(4\).

Câu 32: Rút gọn biểu thức \(A = 2\sqrt 3 a - \sqrt {48} a\) ta được

A. \(A = {\rm{ \;}} - 6\sqrt 3 a\).

B. \(A = 2\sqrt 3 a\).

C. \(A = {\rm{ \;}} - 2\sqrt 3 a\).

D. \(A = 6\sqrt 3 a\).

Câu 33: Trong hình bên, biết \(\angle AMO = 30^\circ \). Số đo \(\angle MOB\) là

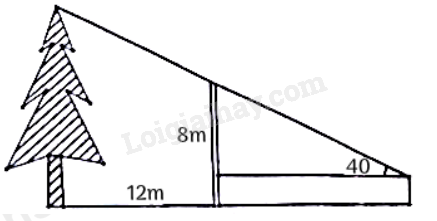
A. \(30^\circ \).

B. \(45^\circ \).

C. \(120^\circ \).

D. \(60^\circ \).

Câu 34: Tập hợp \(M = \left\{ {n \in \mathbb{N}*|n \vdots 3,n \le 30} \right\}\) có số phần tử là

A. 8.

B. 9.

C. 11.

D. 10.

Câu 35: Xác định hàm số \(y = ax + b\), biết đồ thị của hàm số đi qua hai điểm \(A\left( { - 2;1} \right),{\mkern 1mu} {\mkern 1mu} B\left( {1;7} \right)\)

A. \(y = 2x + 5\).

B. \(y = 3x + 7\).

C. \(y = 3x + 1\).

D. \(y = x + 3\).

Câu 36: Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng . Tổng tất cả các giá trị của tham số \(m\) để \(\left( P \right)\) và \(d\) cắt nhau tại hai điểm phân biệt \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) sao cho \(y_1^2 - y_2^2 = 8\left( {x_1^2 - x_2^2} \right)\) là

A. \( - 4\).

B. \(3\).

C. \(4\).

D. \( - 3\).

Câu 37: Một sân trường hình chữ nhật có chu vi là 300m. Hai lần chiều dài hơn ba lần chiều rộng là 50m. Diện tích của sân trường là

A. \(300{m^2}\).

B. \(5000{m^2}\).

C. \(2500{m^2}\).

D. \(150{m^2}\).

Câu 38: Một cái cây ở phía sau bức tường cao 8m và cách bức tường 12m. Một người quan sát đứng trước bức tường ở vị trí chỉ nhìn thấy ngọn cây, khi đó góc nhìn so với phương ngang bằng \(40^\circ \) (hình vẽ). Chiều cao của cây là (làm tròn đến chữ số thập phân)

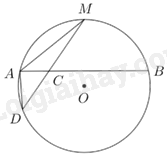
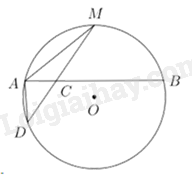
A. 17,07m.

B. 18,07m.

C. 19,07m.

D. 16,07m

Câu 39: Cho đường tròn \(\left( O \right)\) và dây \(AB\), \(M\) là điểm chính giữa của cung nhỏ \(AB\). Lấy điểm \(C\) thuộc đoạn \(AB\), đường thẳng \(MC\) cắt \(\left( O \right)\) tại \(D\) khác \(M\), biết độ dài \(MC = 9cm,\,\,MD = 16cm\) (tham khảo hình vẽ). Độ dài dây \(MA\) là

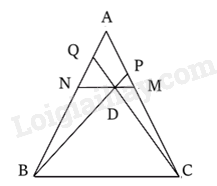
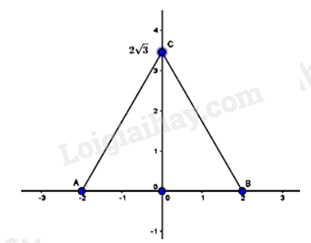
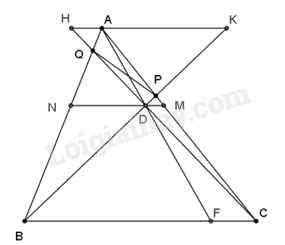
A. \(11cm\).

B. \(25cm\).

C. \(12cm\).

D. \(10cm\).

Câu 40: Tích tất cả các nghiệm của phương trình \(\sqrt {{x^2} - 1} {\rm{ \;}} - {x^2} + 1 = 0\) là

A. \( - \sqrt 2 \).

B. \(2\).

C. \(\sqrt 2 \).

D. \( - 2\).

Câu 41: Cho đường tròn \(\left( {O;2cm} \right)\). Từ điểm \(M\) cách \(O\) một khoảng 4cm, kẻ hai tiếp tuyến \(MA,{\mkern 1mu} {\mkern 1mu} MB\) với (\(A,{\mkern 1mu} {\mkern 1mu} B\) là hai tiếp điểm). Độ dài dây AB là

A. \(2\sqrt 2 cm\).

B. \(2\sqrt 3 cm\).

C. 3cm.

D. \(\sqrt 3 cm\).

Câu 42: Gọi \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x + y}} + \frac{1}{{x - y}} = 3}\\{\frac{1}{{x + y}} - \frac{3}{{x - y}} = 1}\end{array}} \right.\).

Giá trị biểu thức \(\frac{2}{7}{x_0} + \frac{2}{3}{y_0}\) là:

A. \(1\).

B. \( - 1\).

C. \( - 3\).

D. \(3\).

Câu 43: Cho tam giác ABC cân tại \(A\), đường cao \(BH{\mkern 1mu} {\mkern 1mu} \left( {H \in AC} \right)\). Biết \(BH = 4,{\mkern 1mu} {\mkern 1mu} \angle B = 65^\circ \). Diện tích tam giác \(ABC\) là (làm tròn kết quả đến chữ số thập phân thứ hai)

A. \(10,44\)(đvdt)

B. \(10,45\)(đvdt)

C. \(5,23\)(đvdt)

D. \(5,22\) (đvdt)

Câu 44: Với giá trị dương nào của tham số \(m\) thì khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(d:y = x + m - 1\) bằng \(\sqrt 2 \)?

A. \(m = 1\).

B. \(m = 2\).

C. \(m = 3\).

D. \(m = 4\).

Câu 45: Cho phương trình \(\left( {{m^2}{x^2} + 4x + 1} \right)\left( {x - 2023} \right) = 0\). Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để phương trình đã cho có 3 nghiệm phân biệt?

A. 1.

B. 3.

C. 4.

D. 2.

Câu 46: Cho hai đường thẳng \({d_1}:y = \sqrt 3 x + 2\sqrt 3 ,{\mkern 1mu} {\mkern 1mu} {d_2}:y = {\rm{ \;}} - \sqrt 3 x + 2\sqrt 3 \). Đường thẳng \({d_1}\) cắt trục hoành tại \(A,{\mkern 1mu} {\mkern 1mu} {d_2}\) cắt trục hoành tại \(B;{\mkern 1mu} {\mkern 1mu} {d_1},{\mkern 1mu} {\mkern 1mu} {d_2}\) cắt nhau tại \(C\). Diện tích tam giác ABC là

A. \(2\sqrt 3 \) (đvdt)

B. \(4\sqrt 3 \) (đvdt)

C. \(16\sqrt 3 \) (đvdt)

D. \(8\sqrt 3 \) (đvdt)

Câu 47: Cho tam giác ABC cân tại \(A\) có \(AB = 4,{\mkern 1mu} {\mkern 1mu} M \in AC,{\mkern 1mu} {\mkern 1mu} N \in AB\) sao \(MN\parallel BC,{\mkern 1mu} {\mkern 1mu} \frac{{AM}}{{MC}} = \frac{2}{3}\).

Điểm \(D \in MN\), đường thẳng BD cắt AC tại \(P\), đường thẳng CD cắt AB tại \(Q\). Khi đó \(\frac{1}{{BQ}} + \frac{1}{{CP}}\) có giá trị là

A. \(\frac{{13}}{{20}}\).

B. \(\frac{{32}}{{49}}\).

C. \(\frac{2}{3}\).

D. \(\frac{3}{5}\).

Câu 48: Cho đường thẳng \(d:y = \left( {{m^2} + 2m + 3} \right)x - 1\). Gọi \(A,{\mkern 1mu} {\mkern 1mu} B\) là giao điểm của đường thẳng \(d\) với hai trục tọa độ, khi đó diện tích lớn nhất của tam giác OAB là

A. \(\frac{1}{2}\).

B. \(\frac{1}{8}\).

C. \(\frac{1}{4}\).

D. \(\frac{1}{3}\).

Câu 49: Cho phương trình \({x^2} + 2x - m + 5 = 0\). Tất cả các giá trị của tham số \(m\) để phương trình đã cho có hai nghiệm âm phân biệt là:

A. \(m < 5\).

B. \(m > 4\).

C. \(4 < m < 5\).

D. \( - 5 < m < 4\).

Câu 50: Phương trình \(\frac{9}{{x - \sqrt x {\rm{ \;}} - 2}} + \frac{{2\sqrt x {\rm{ \;}} + 5}}{{\sqrt x {\rm{ \;}} + 1}} - \frac{{\sqrt x {\rm{ \;}} - 1}}{{\sqrt x {\rm{ \;}} - 2}} = 2\sqrt x {\rm{ \;}} + 1\) với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 4\) có nghiệm duy nhất dạng \(x = a + b\sqrt 2 \) trong đó \(a,{\mkern 1mu} {\mkern 1mu} b \in \mathbb{Z}\). Giá trị biểu thức \(2a - b\) là

A. 3

B. 6

C. 4

D. 5

-----HẾT-----

Lời giải chi tiết

Câu 1 (NB):

Phương pháp:

Hàm số bậc nhất là hàm số có dạng \(y = ax + b,{\mkern 1mu} {\mkern 1mu} a \ne 0\)

Cách giải:

Ta có: hàm số bậc nhất là \(y = 3x + 2\)

Chọn C.

Câu 2 (NB):

Phương pháp:

Sử dụng hệ thức lượng trong tam giác

Cách giải:

Ta có tam giác ABC vuông tại \(A\), đường cao \(AH{\mkern 1mu} {\mkern 1mu} \left( {H \in BC} \right)\)

Suy ra \(A{H^2} = BH.CH\)

Chọn A.

Câu 3 (NB):

Phương pháp:

Tổng các góc trong tứ giác bằng \(360^\circ \)

Cách giải:

Ta có: \(\angle A + \angle B + \angle C + \angle D = 360^\circ \)

\(\begin{array}{*{20}{l}}{ \Rightarrow 80^\circ  + 110^\circ  + 100^\circ  + \angle D = 360^\circ }\\{ \Rightarrow \angle D = 360^\circ  - 100^\circ  - 110^\circ  - 80^\circ }\\{ \Rightarrow \angle D = 70^\circ }\end{array}\)

Chọn D.

Câu 4 (NB):

Phương pháp:

Vị trí tương đối của hai đường tròn: hai đường tròn phân biệt có nhiều nhất 2 điểm chung.

Cách giải:

Hai đường tròn phân biệt có nhiều nhất 2 điểm chung

Chọn D.

Câu 5 (TH):

Phương pháp:

Phương trình bậc hai một ẩn có dạng \(a{x^2} + bx + c = 0,{\mkern 1mu} {\mkern 1mu} a \ne 0\)

Cách giải:

Phương trình bậc hai một ẩn là \({x^2} - 2x - 3 = 0\)

Chọn D.

Câu 6 (TH):

Phương pháp:

Các góc lượng giác đặc biệt: \(\sin 30^\circ  = \frac{1}{2}\)

Cách giải:

Ta có: \(\sin 30^\circ  = \frac{1}{2}\)

Chọn A.

Câu 7 (NB):

Phương pháp:

Thay lần lượt cặp số \(\left( {1;2} \right)\) vào các phương trình

Cách giải:

Thay \(x = 1;y = 2\) vào \(3x + 2y = 7\) ta được: \(3.1 + 2.2 = 7\)

Do đó cặp số \(\left( {1;2} \right)\) là nghiệm của phương trình \(3x + 2y = 7\)

Chọn C.

Câu 8 (NB):

Phương pháp:

Công thức tính diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi rh\).

Thay \(r,{\mkern 1mu} {\mkern 1mu} h\) vào công thức đã cho

Cách giải:

Ta có: \({S_{xq}} = 2\pi rh = 2\pi .2.3 = 12\pi \)(đvdt)

Chọn B.

Câu 9 (TH):

Phương pháp:

Thay tọa độ các điểm vào phương trình đường thẳng.

Cách giải:

Thay \(x = {\rm{ \;}} - 1;y = {\rm{ \;}} - 3\) vào đường thẳng \(y = 2x - 1\) ta được:\( - 3 = 2.\left( { - 1} \right) - 1\)

Do đó đường thẳng \(y = 2x - 1\) đi qua điểm \(M\left( { - 1; - 3} \right)\)

Chọn B.

Câu 10 (NB):

Phương pháp:

Đưa về phương trình tích A.B = 0

Cách giải:

Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 3}\end{array}} \right.\)

Chọn A.

Câu 11 (NB):

Phương pháp:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung.

Bước 3: Lập tích các tích thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.

Tích đó là ƯCLN phải tìm.

Cách giải:

Ta có: \(6 = 2.3,{\mkern 1mu} {\mkern 1mu} 9 = {3^2}\)

Do đó ước chung lớn nhất của \(6,{\mkern 1mu} {\mkern 1mu} 9\) là 3

Chọn C.

Câu 12 (TH):

Phương pháp:

Tính chất của tam giác cân: Hai cạnh bên bằng nhau.

Cách giải:

Vì tam giác ABC cân tại \(A \Rightarrow AB = AC\)

Chọn C.

Câu 13 (TH):

Phương pháp:

Đường thẳng \(y = ax + b{\mkern 1mu} {\mkern 1mu} \left( {a \ne 0} \right)\) có hệ số góc là \(a\)

Cách giải:

Hệ số góc \(a\) của đường thẳng \(y = 2x + 3\) là \(a = 2\)

Chọn B.

Câu 14 (NB):

Phương pháp:

Góc nội tiếp chắn nửa đường tròn là góc vuông

Cách giải:

Góc nội tiếp chắn nửa đường tròn là góc vuông

Chọn A.

Câu 15 (NB):

Phương pháp:

Tính giá trị biểu thức.

Cách giải:

Ta có: \(\sqrt 9 {\rm{ \;}} + 5 = 3 + 5 = 8\)

Chọn B.

Câu 16 (NB):

Phương pháp:

Điều kiện xác định của hàm số \(\sqrt {f\left( x \right)} \) là \(f\left( x \right) \ge 0\)

Cách giải:

Điều kiện xác định của \(\sqrt {x - 10} \) là \(x - 10 \ge 0 \Leftrightarrow x \ge 10\)

Chọn C.

Câu 17 (TH):

Phương pháp:

Dây có độ dài lớn nhất của đường tròn là đường kính

Cách giải:

Dây có độ dài lớn nhất của đường tròn là đường kính

Đường kính của đường tròn \(\left( {O;12cm} \right)\) là 24cm

Chọn C.

Câu 18 (NB):

Phương pháp:

Sử dụng: \({a^m}.{a^n} = {a^{m + n}}\)

Cách giải:

Ta có: \({a^3}.{a^5} = {a^{3 + 5}} = {a^8}\)

Chọn C.

Câu 19 (NB):

Phương pháp:

Đặt nhân tử chung.

Cách giải:

Ta có: \({x^2} - 5x = x\left( {x - 5} \right)\)

Chọn D.

Câu 20 (NB):

Phương pháp:

Số đo cung nhỏ AB bằng góc ở tâm\(\angle AOB\)

Cách giải:

Xét (O) có: \(\angle AOB = 60^\circ \)

Suy ra số đo cung nhỏ AB là \(60^\circ \)

Chọn D.

Câu 21 (NB):

Phương pháp:

Giải hệ phương trình bẳng phương pháp cộng đại số.

Cách giải:

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{3x - y = 5}\\{5x + 4y = 14}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{12x - 4y = 20}\\{5x + 4y = 14}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{17x = 34}\\{5x + 4y = 14}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{10 + 4y = 14}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 1}\end{array}} \right.\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right)\) là \(\left( {2;1} \right)\)

Chọn B.

Câu 22 (NB):

Phương pháp:

Thay giá trị \(x = 2,{\mkern 1mu} {\mkern 1mu} x = {\rm{ \;}} - 2\) vào các hàm số \(f\left( x \right)\)

Cách giải:

Xét \(f\left( x \right) = \frac{{{x^2}}}{2}\)

Ta có \(f(2) = \frac{{{2^2}}}{2} = 2;f( - 2) = \frac{{{{\left( { - 2} \right)}^2}}}{2} = 2\)

Suy ra \(f\left( 2 \right) = f\left( { - 2} \right)\)

Chọn D.

Câu 23 (TH):

Phương pháp:

Thay tọa độ điểm \(\left( {1; - 1} \right)\) vào phương trình đường thẳng rồi tìm \(m\)

Cách giải:

Vì đồ thị hàm số \(y = \left( {m - 2} \right){x^2}\) đi qua điểm \(P\left( {1; - 1} \right)\) nên \(m - 2 = {\rm{ \;}} - 1 \Rightarrow m = 1\)

Chọn B.

Câu 24 (NB):

Phương pháp:

Sử dụng hệ thức Vi – ét: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)

Cách giải:

Ta có: \(\Delta {\rm{ \;}} = 9 - 4.2 = 1 > 0\). Do đó phương trình có 2 nghiệm phân biệt

Áp dụng định lý Viete ta có \({x_1}.{x_2} = \frac{c}{a} = 2\)

Chọn D.

Câu 25 (TH):

Phương pháp:

Gọi \(I\) là trung điểm của AB.

Sử dụng định lí: Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì

vuông góc với dây ấy.

Khi đó OI là khoảng cách từ O đến AB.

Sử dụng định lý Py-ta-go trong tam giác vuông để tính OI

Cách giải:

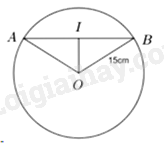
Gọi \(I\) là trung điểm của \(AB \Rightarrow IA = IB = \frac{{AB}}{2} = \frac{{24}}{2} = 12\left( {cm} \right)\)

Vì tam giác OAB cân tại \(O \Rightarrow OI \bot AB\)

Áp dụng định lý Py-ta-go trong tam giác OIB:

\(OI = \sqrt {O{B^2} - I{B^2}} {\rm{ \;}} = \sqrt {{{15}^2} - {{12}^2}} {\rm{ \;}} = 9\left( {cm} \right)\)

Vậy khoảng cách từ \(O\) đến dây AB là 9cm

Chọn B.

Câu 26 (TH):

Phương pháp:

Thể tích hình nón có chiều cao \(h\) và bán kính đáy \(r\) là \(V = \frac{1}{3}\pi {r^2}h\)

Cách giải:

Thể tích hình nón có chiều cao \(h = 2cm\) và bán kính đáy \(r = 3cm\) là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.3^2}.2 = 6\pi \left( {c{m^3}} \right)\)

Chọn C.

Câu 27 (TH):

Phương pháp:

Diện tích đường tròn có bán kính đáy \(R\) là \(S = \pi {R^2}\), từ đó tìm bán kính rồi tính chu vi của đường tròn

Cách giải:

Gọi \(R\) là bán kính của đường tròn

Khi đó \(\pi {R^2} = 64\pi {\rm{ \;}} \Rightarrow R = 8\left( {cm} \right)\)

Chu vi đường tròn là \(C = 2\pi R = 2\pi .8 = 16\pi \left( {cm} \right)\)

Chọn D.

Câu 28 (TH):

Phương pháp:

Sử dụng: \(\sin x{\rm{ \;}} = \cos \left( {90^\circ  - x} \right)\)

Cách giải:

Ta có: \(\sin 25^\circ  = \cos \left( {90^\circ  - 25^\circ } \right) = \cos 65^\circ \)

Chọn C.

Câu 29 (TH):

Phương pháp:

Với \(a < 0,{\mkern 1mu} \sqrt {{a^2}} {\rm{ \;}} = \left| a \right| = {\rm{ \;}} - a\)

Cách giải:

Với \(a < 0,{\mkern 1mu} \sqrt {{a^2}} {\rm{ \;}} = \left| a \right| = {\rm{ \;}} - a\)

Khi đó \(P = \frac{{\sqrt {{a^2}} }}{2} + \frac{{3a}}{2} = \frac{{ - a}}{2} + \frac{{3a}}{2} = \frac{{2a}}{2} = a\)

Chọn D.

Câu 30 (TH):

Phương pháp:

Tìm các nghiệm của phương trình rồi tính tích.

Cách giải:

Ta có: \(\left( {x - 1} \right)\left( {{x^2} - 4} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 1 = 0}\\{{x^2} - 4 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{{x^2} = 4}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 2}\\{x = {\rm{ \;}} - 2}\end{array}} \right.\)

Tích các nghiệm là \(1.2.\left( { - 2} \right) = {\rm{ \;}} - 4\)

Chọn A.

Câu 31 (TH):

Phương pháp:

Biểu diễn \(x\) theo \(y\) rồi thay vào phương trình \(2x - y = 8\)

Cách giải:

Vì \(\frac{x}{y} = \frac{3}{2} \Rightarrow x = \frac{3}{2}y\)

Khi đó \(3y - y = 8 \Rightarrow 2y = 8 \Rightarrow y = 4\)

Chọn D.

Câu 32 (TH):

Phương pháp:

Rút gọn biểu thức, đưa một số ra ngoài dấu căn: \(\sqrt {{a^2}b} {\rm{ \;}} = a\sqrt b \)

Cách giải:

Ta có: \(A = 2\sqrt 3 a - \sqrt {48} a = 2\sqrt 3 a - 4\sqrt 3 a = {\rm{ \;}} - 2\sqrt 3 a\)

Chọn A.

Câu 33 (TH):

Phương pháp:

Sử dụng tính chất của tam giác cân và tính chất của góc ngoài

Cách giải:

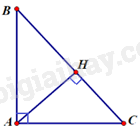
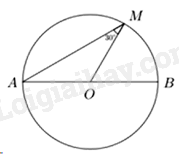
Vì \(\Delta MOA\) cân tại \(O\) nên \(\angle OMA = \angle MAO\)

Ta có: \(\angle MOB = \angle OMA + \angle MAO = 2\angle OMA = 2.30^\circ  = 60^\circ \)

Chọn D.

Câu 34 (TH):

Phương pháp:

Tìm các phần tử thuộc tập hợp \(M\)

Cách giải:

Ta có: \(n \in \mathbb{N}*,{\mkern 1mu} {\mkern 1mu} n \vdots 3,{\mkern 1mu} {\mkern 1mu} n \le 30 \Rightarrow n \in \left\{ {3;6; \ldots ;30} \right\}\)

Khi đó \(M\) có 10 phần tử

Chọn D.

Câu 35 (TH):

Phương pháp:

Lập đường thẳng đi qua hai điểm, từ đó có hệ phương trình, giải hệ bằng phương pháp cộng đại số.

Cách giải:

Vì đồ thị hàm số đi qua hai điểm \(A\left( { - 2;1} \right),{\mkern 1mu} {\mkern 1mu} B\left( {1;7} \right)\) nên \(\left\{ {\begin{array}{*{20}{l}}{ - 2a + b = 1}\\{a + b = 7}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3a = 6}\\{a + b = 7}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{2 + b = 7}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = 5}\end{array}} \right.\)

Hàm số cần tìm là \(y = 2x + 5\)

Chọn A.

Câu 36 (VD):

Phương pháp:

- Xét phương trình hoành độ giao điểm

- Tìm điều kiện để phương trình đó có 2 nghiệm phân biệt

- Áp dụng định lý Vi-ét để giải điều kiện

Cách giải:

Xét phương trình hoành độ giao điểm \(\left( P \right),{\mkern 1mu} {\mkern 1mu} d\): \({x^2} = \left( {m + 1} \right)x + 2 \Leftrightarrow {x^2} - \left( {m + 1} \right)x - 2 = 0\)

\(\Delta {\rm{ \;}} = {\left( {m + 1} \right)^2} - 4.\left( { - 2} \right) = {\left( {m + 1} \right)^2} + 8 > 0,{\mkern 1mu} {\mkern 1mu} \forall m \in \mathbb{R}\)

Do đó phương trình luôn có 2 nghiệm phân biệt \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) với mọi \(m\)

Áp dụng định lý Viete ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = m + 1}\\{{x_1}{x_2} = {\rm{ \;}} - 2}\end{array}} \right.\)

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{y_1} = {x_1}^2 \Rightarrow {y_1}^2 = x_1^4}\\{{y_2} = {x_2}^2 \Rightarrow {y_2}^2 = x_2^4}\end{array}} \right.\)

Khi đó \(x_1^4 - x_2^4 = 8\left( {x_1^2 - x_2^2} \right)\)

\(\begin{array}{*{20}{l}}{ \Leftrightarrow \left( {x_1^2 - x_2^2} \right)\left( {x_1^2 + x_2^2} \right) = 8\left( {x_1^2 - x_2^2} \right)}\\{ \Leftrightarrow \left( {x_1^2 - x_2^2} \right)\left( {x_1^2 + x_2^2 - 8} \right) = 0}\\{ \Leftrightarrow x_1^2 + x_2^2 - 8 = 0{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} {x_1} \ne {x_2} \Rightarrow x_1^2 \ne x_2^2} \right)}\\{ \Leftrightarrow x_1^2 + x_2^2 = 8}\\{ \Leftrightarrow {{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} = 8}\\{ \Rightarrow {{\left( {m + 1} \right)}^2} + 4 = 8}\\{ \Leftrightarrow {{\left( {m + 1} \right)}^2} = 4}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m + 1 = 2}\\{m + 1 =  - 2}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 1}\\{m =  - 3}\end{array}} \right.}\end{array}\)

Tổng các giá trị của tham số \(m\) thỏa mãn là \(1 - 3 = {\rm{ \;}} - 2\)

Chọn D.

Câu 37 (TH):

Phương pháp:

Giải bài toán bằng cách lập hệ phương trình:

- Gọi chiều dài, chiều rộng hình chữ nhật lần lượt là \(a,{\mkern 1mu} {\mkern 1mu} b{\mkern 1mu} {\mkern 1mu} \left( {a > 0,{\mkern 1mu} {\mkern 1mu} b > 0} \right)\)

- Lập hệ phương trình, tìm \(a,{\mkern 1mu} {\mkern 1mu} b\)

Cách giải:

Gọi chiều dài, chiều rộng hình chữ nhật lần lượt là \(a,{\mkern 1mu} {\mkern 1mu} b{\mkern 1mu} {\mkern 1mu} \left( {a > 0,{\mkern 1mu} {\mkern 1mu} b > 0} \right)\)

Chu vi sân trường hình chữ nhật là \(300m \Rightarrow a + b = 150\) (1)

Hai lần chiều dài hơn ba lần chiều rộng là 50m nên \(2a - 3b = 50\) (2)

Từ (1) và (2) ta có \(\left\{ {\begin{array}{*{20}{l}}{a + b = 150}\\{2a - 3b = 50}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2a + 2b = 300}\\{2a - 3b = 50}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{5b = 250}\\{2a - 3b = 50}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = 50}\\{2a - 150 = 50}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = 50}\\{a = 100}\end{array}} \right.\)

Diện tích sân trường là \(S = 100.50 = 5000\left( {{m^2}} \right)\)

Chọn B.

Câu 38 (TH):

Phương pháp:

- Sử dụng tính chất của đường thẳng song song

- Sử dụng định lý tan trong tam giác

Cách giải:

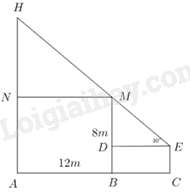
Xét cấu trúc như hình trên: \(AB = 12,{\mkern 1mu} {\mkern 1mu} BM = 8,{\mkern 1mu} {\mkern 1mu} \angle MED = 40^\circ \)

Ta có: \(DE\parallel MN \Rightarrow \angle HMN = \angle MED = 40^\circ \)

Xét tam giác HMN vuông tại \(N\) có:

 \(HN = MN.\tan \angle HMN = 12.\tan 40^\circ  \approx 10,07\)

Vậy chiều cao của cây là \(10,07 + 8 = 18,07\left( m \right)\)

Chọn B.

Câu 39 (TH):

Phương pháp:

- Chứng minh $\Delta MAC\backsim \Delta MDA$

- Tính MA

Cách giải:

Ta có: \(M\) là điểm chính giữa của cung nhỏ AB nên

Lại có:

Suy ra \(\angle MAC = \angle MDA\)

Xét \(\Delta MAC\) và \(\Delta MDA\) có: \(\angle MAC = \angle MDA\); \(\angle AMD{\mkern 1mu} {\mkern 1mu} chung\)

$\Rightarrow \Delta MAC\backsim \Delta MDA(\text{g-g})$\( \Rightarrow \frac{{MA}}{{MD}} = \frac{{MC}}{{MA}}\) (các cạnh tương ứng tỉ lệ)

\( \Rightarrow M{A^2} = MC.MD = 9.16\)

\( \Rightarrow MA = 12(cm)\)

Chọn C.

Câu 40 (VD):

Phương pháp:

- Tìm ĐKXĐ

- Đưa về phương trình tích

Cách giải:

ĐKXĐ: \({x^2} - 1 \ge 0 \Leftrightarrow {x^2} \ge 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x \ge 1}\\{x \le {\rm{ \;}} - 1}\end{array}} \right.\)

Ta có:

\(\begin{array}{*{20}{l}}{\sqrt {{x^2} - 1}  - {x^2} + 1 = 0}\\{ \Leftrightarrow \sqrt {{x^2} - 1}  - \left( {{x^2} - 1} \right) = 0}\\{ \Leftrightarrow \sqrt {{x^2} - 1} \left( {1 - \sqrt {{x^2} - 1} } \right) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sqrt {{x^2} - 1}  = 0}\\{\sqrt {{x^2} - 1}  = 1}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 1 = 0}\\{{x^2} - 1 = 1}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} = 1}\\{{x^2} = 2}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x =  - 1}\\{x = \sqrt 2 }\\{x =  - \sqrt 2 }\end{array}} \right.}\end{array}\)

Vậy tích các nghiệm là \(1.( - 1).\sqrt 2 .\left( { - \sqrt 2 } \right) = 2\)

Chọn B.

Câu 41 (VD):

Phương pháp:

Gọi H là giao điểm của AB và MO

Sử dụng tính chất 2 tiếp tuyến cắt nhau.

Áp dụng hệ thức lượng trong tam giác vuông, định lí Py-ta-go để tính độ dài các đoạn thẳng.

Cách giải:

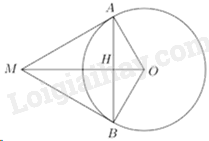
Gọi \(H\) là giao điểm của AB và MO

Xét (O) có 2 tiếp tuyến MA, MB cắt nhauu tại M nên \(MA = MB,{\mkern 1mu} {\mkern 1mu} OA = OB\)

Suy ra OM là đường trung trực của AB

Xét tam giác MAO vuông tại \(A\) có \(AH \bot MO:{\mkern 1mu} {\mkern 1mu} \)

\( \Rightarrow O{A^2} = OH.OM \Rightarrow OH = \frac{{O{A^2}}}{{OM}} = \frac{{{2^2}}}{4} = 1\)

Áp dụng định lý Py-ta-go vào tam giác OAH vuông tại \(H\):

\(AH = \sqrt {O{A^2} - O{H^2}} {\rm{ \;}} = \sqrt {{2^2} - {1^1}} {\rm{ \;}} = \sqrt 3 \)

Do đó \(AB = 2AH = 2\sqrt 3 {\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\)

Chọn B.

Câu 42 (VD):

Phương pháp:

Giải hệ phương trình bằng phương pháp cộng đại số

Cách giải:

ĐKXĐ: \(x \ne y \ne 0\)

Ta có:

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x + y}} + \frac{1}{{x - y}} = 3}\\{\frac{1}{{x + y}} - \frac{3}{{x - y}} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x + y}} + \frac{1}{{x - y}} = 3}\\{\frac{2}{{x + y}} - \frac{6}{{x - y}} = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x + y}} + \frac{1}{{x - y}} = 3}\\{\frac{7}{{x - y}} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x + y}} + \frac{1}{7} = 3}\\{x - y = 7}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{2}{{x + y}} = \frac{{20}}{7}}\\{x - y = 7}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + y = \frac{7}{{10}}}\\{x - y = 7}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{{77}}{{20}}}\\{y = \frac{{ - 63}}{{20}}}\end{array}} \right.\end{array}\)

Khi đó \(\frac{2}{7}{x_0} + \frac{2}{3}{y_0} = \frac{2}{7}.\frac{{77}}{{20}} - \frac{2}{3}.\frac{{63}}{{20}} = {\rm{ \;}} - 1\)

Chọn B.

Câu 43 (VD):

Phương pháp:

Tính góc A trong tam giác ABC.

Sử dụng tỉ số lượng giác trong tam giác ABH vuông H.

Cách giải:

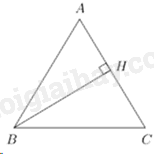
Ta có: \(\angle BAC = 180^\circ  - 2\angle B = 180^\circ  - 2.65^\circ  = 50^\circ \) (do tam giác ABC cân tại \(A\))

Tam giác ABH vuông tại \(H\) nên \(AB = \frac{{BH}}{{\sin 50^\circ }} = \frac{4}{{\sin 50^\circ }} = 5,22\)

Diện tích tam giác ABC là \({S_{ABC}} = \frac{1}{2}BH.AB = \frac{1}{2}.4.5,22 = 10,44\) (đvdt)

Chọn A.

Câu 44 (VD):

Phương pháp:

- Gọi giao điểm của d với hai trục tọa độ Ox, Oy lần lượt là A, B

- Gọi OH vuông góc với AB tại H

- Tính \(OA,{\mkern 1mu} {\mkern 1mu} OB\) rồi dùng hệ thức lượng tính OH

Cách giải:

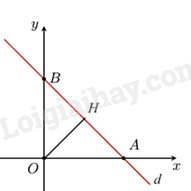
Gọi \(A,{\mkern 1mu} {\mkern 1mu} B\) lần lượt là giao điểm của \(d\) với trục \(Ox,{\mkern 1mu} {\mkern 1mu} Oy\)

Khi đó \(A\left( {1 - m;0} \right),{\mkern 1mu} {\mkern 1mu} B\left( {0;m - 1} \right)\)

Suy ra \(OA = \left| {1 - m} \right|,{\mkern 1mu} {\mkern 1mu} OB = \left| {m - 1} \right|\)

Áp dụng hệ thức lượng trong tam giác OAB vuông tại \(O\) có OH vuông góc với AB

\( \Rightarrow \frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}\)

\(\begin{array}{*{20}{l}}{ \Rightarrow \frac{1}{{O{H^2}}} = \frac{1}{{{{\left( {m - 1} \right)}^2}}} + \frac{1}{{{{\left( {m - 1} \right)}^2}}} = \frac{2}{{{{\left( {m - 1} \right)}^2}}}}\\{ \Rightarrow OH = \frac{{\left| {m - 1} \right|}}{{\sqrt 2 }}}\end{array}\)

Từ giả thiết suy ra \(\frac{{\left| {m - 1} \right|}}{{\sqrt 2 }} = \sqrt 2 {\rm{ \;}} \Rightarrow \left| {m - 1} \right| = 2 \Rightarrow \left[ {\begin{array}{*{20}{l}}{m - 1 = 2}\\{m - 1 = {\rm{ \;}} - 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 3}\\{m = {\rm{ \;}} - 1}\end{array}} \right.\)

Mà \(m > 0 \Rightarrow m = 3\)

Chọn C.

Câu 45 (VD):

Phương pháp:

Biện luận nghiệm của phương trình bậc hai

Cách giải:

\(\left( {{m^2}{x^2} + 4x + 1} \right)\left( {x - 2023} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m^2}{x^2} + 4x + 1 = 0{\mkern 1mu} {\mkern 1mu} \left( 1 \right)}\\{x = 2023}\end{array}} \right.\)

Để phương trình đã cho có 3 nghiệm phân biệt thì (1) phải có 2 nghiệm phân biệt khác 2023

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' = 4 - {m^2} > 0}\\{2023{m^2} + 4.2023 + 1 \ne 0}\\{m \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} < 4}\\{m \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 2 < m < 2}\\{m \ne 0}\end{array}} \right.\)

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;1} \right\}\)

Chọn D.

Câu 46 (VD):

Phương pháp:

Xác định giao điểm của hai đường thẳng.

Từ đó tính diện tích tam giác ABC.

Cách giải:

Ta có: \(A\left( { - 2;0} \right),{\mkern 1mu} {\mkern 1mu} B\left( {0;2} \right)\)

Tọa độ \(C\) là nghiệm của hệ:\(\left\{ {\begin{array}{*{20}{l}}{y = \sqrt 3 x + 2\sqrt 3 }\\{y = {\rm{ \;}} - \sqrt 3 x + 2\sqrt 3 }\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}\\{y = 2\sqrt 3 }\end{array}} \right.\)

Ta có: \(OC = 2\sqrt 3 \)

\(AB = OA + OB = 2 + 2 = 4\)

Diện tích tam giác ABC là \(\frac{1}{2}OC.AB = \frac{1}{2}.2\sqrt 3 .4 = 4\sqrt 3 \) (đvdt)

Chọn B.

Câu 47 (VDC):

Phương pháp:

Gọi F là giao điểm của AD và BC

Qua A kẻ đường thẳng song song với BC, cắt BP tại K, cắt CQ tại H

Áp dụng định lí Ta-ét suy ra ra các cặp cạnh tương ứng tỉ lệ.

Sử dụng các kiến thức tính chất dãy tỉ số bằng nhau.

Cách giải:

Gọi F là giao điểm của AD và BC

Qua A kẻ đường thẳng song song với BC, cắt BP tại K, cắt CQ tại H

Suy ra HK // MN // BC

Áp dụng định lí Ta-lét ta có:

Vì \(AK\parallel BF \Rightarrow \frac{{AK}}{{BF}} = \frac{{AD}}{{DF}}\)

Vì \(AH\parallel FC \Rightarrow \frac{{AH}}{{FC}} = \frac{{AD}}{{DF}}\)

\( \Rightarrow \frac{{AK}}{{BF}} = \frac{{AD}}{{DF}} = \frac{{AH}}{{FC}} = \frac{{AH + AK}}{{BF + FC}} = \frac{{HK}}{{BC}}\) (tính chất dãy tỉ số bằng nhau)

Lại có:  \(\frac{{AQ}}{{BQ}} = \frac{{AH}}{{BC}}\quad (AH\parallel BC)\)

           \(\frac{{AP}}{{CP}} = \frac{{AK}}{{BC}}(AK\parallel BC)\)

\( \Rightarrow \frac{{AQ}}{{BQ}} + \frac{{AP}}{{CP}} = \frac{{AH}}{{BC}} + \frac{{AK}}{{BC}} = \frac{{HK}}{{BC}} = \frac{{AD}}{{DF}}\)

Mà \(\frac{{AM}}{{MC}} = \frac{2}{3} \Rightarrow \frac{{AD}}{{DF}} = \frac{2}{3}\)

\(\begin{array}{*{20}{l}}{ \Rightarrow \frac{{AQ}}{{BQ}} + \frac{{AP}}{{CP}} = \frac{2}{3}}\\{ \Rightarrow \frac{{AQ}}{{BQ}} + 1 + \frac{{AP}}{{CP}} + 1 = \frac{2}{3} + 2}\\{ \Rightarrow \frac{{AB}}{{BQ}} + \frac{{AC}}{{CP}} = \frac{8}{3}}\\{ \Rightarrow \frac{4}{{BQ}} + \frac{4}{{CP}} = \frac{8}{3}}\\{ \Rightarrow \frac{1}{{BQ}} + \frac{1}{{CP}} = \frac{2}{3}}\end{array}\)

Chọn C.

Câu 48 (VD):

Phương pháp:

Gọi \(A,{\mkern 1mu} {\mkern 1mu} B\) là giao điểm của đường thẳng \(d\) với hai trục tọa độ Ox, Oy.

Biểu diễn diện tích tam giác OAB và tìm GTLN của biểu thức.

Cách giải:

Ta có: \(A\left( {0; - 1} \right),{\mkern 1mu} {\mkern 1mu} B\left( {\frac{1}{{{m^2} + 2m + 3}};0} \right)\). Suy ra \(OA = 1,{\mkern 1mu} {\mkern 1mu} OB = \frac{1}{{{m^2} + 2m + 3}}\)

\({S_{OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.1.\frac{1}{{{m^2} + 2m + 3}} = \frac{1}{{2\left( {{m^2} + 2m + 3} \right)}}\)

Ta có: \({m^2} + 2m + 3 = {\left( {m + 1} \right)^2} + 2 \ge 2 \Rightarrow \frac{1}{{2\left( {{m^2} + 2m + 3} \right)}} \le \frac{1}{4}\)

Hay \({S_{OAB}} \le \frac{1}{4}\)

Dấu  xảy ra khi và chỉ khi \(m = {\rm{ \;}} - 1\)

Chọn C.

Câu 49 (VD):

Phương pháp:

- Tìm điều kiện để phương trình có 2 nghiệm phân biệt

- Sử dụng định lý Vi-ét

Cách giải:

Ta có: \(\Delta ' = 1 - \left( { - m + 5} \right) = m - 4\)

Để phương trình đã cho có 2 nghiệm phân biệt thì \(m - 4 > 0 \Leftrightarrow m > 4\)

Áp dụng định lý Viete ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - 2}\\{{x_1}{x_2} = {\rm{ \;}} - m + 5}\end{array}} \right.\)

Để phương trình có 2 nghiệm âm phân biệt thì \( - m + 5 > 0 \Leftrightarrow m < 5\)

Kết hợp hai điều kiện trên ta được \(4 < m < 5\)

Chọn C.

Câu 50 (VDC):

Phương pháp:

Rút gọn vế trái rồi giải phương trình

Cách giải:

Ta có: \(\frac{9}{{x - \sqrt x {\rm{ \;}} - 2}} + \frac{{2\sqrt x {\rm{ \;}} + 5}}{{\sqrt x {\rm{ \;}} + 1}} - \frac{{\sqrt x {\rm{ \;}} - 1}}{{\sqrt x {\rm{ \;}} - 2}} = 2\sqrt x {\rm{ \;}} + 1\)

\( \Leftrightarrow \frac{9}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}} + \frac{{\left( {2\sqrt x  + 5} \right)\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}} - \frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}} = 2\sqrt x  + 1\)

\( \Leftrightarrow \frac{{9 + 2x + \sqrt x  - 10 - x + 1}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}} = 2\sqrt x  + 1\)

\( \Leftrightarrow \frac{{x + \sqrt x }}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right)}} = 2\sqrt x  + 1\)

\( \Leftrightarrow \frac{{\sqrt x }}{{\sqrt x  - 2}} = 2\sqrt x  + 1\)

\( \Leftrightarrow \left( {2\sqrt x  + 1} \right)\left( {\sqrt x  - 2} \right) = \sqrt x \)

\(\begin{array}{l} \Leftrightarrow 2x - 4\sqrt x  - 2 = 0\\ \Leftrightarrow x - 2\sqrt x  - 1 = 0\\ \Leftrightarrow x - 2\sqrt x  + 1 = 2\\ \Leftrightarrow {(\sqrt x  - 1)^2} = 2\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sqrt x  - 1 = \sqrt 2 }\\{\sqrt x  - 1 =  - \sqrt 2 (L)}\end{array}} \right.\\ \Leftrightarrow \sqrt x  = \sqrt 2  + 1\\ \Leftrightarrow x = 3 + 2\sqrt 2 \end{array}\)

Vậy \(2a - b = 2.3 - 2 = 4\)

Chọn C.