Đề thi vào 10 môn Toán Hậu Giang năm 2020Tải vềA. Trắc nghiệm (2 điểm) Câu 1. Tìm số thực m để hàm số Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài A. Trắc nghiệm (2 điểm) Câu 1. Tìm số thực m để hàm số \(y = \left( {2 - m} \right)x + 1\) nghịch biến trên ℝ A. \(m > 0\) B. \(m < 2\) C. \(m \ne 2\) D. \(m > 2\) Câu 2. Phương trình \({x^2} - 5x - 6 = 0\) có bao nhiêu nghiệm dương? A. 0 B. 1 C. 2 D. 3 Câu 3. Tìm điều kiện của \(x\) để biểu thức \(P = \dfrac{{2 + x}}{{\sqrt {x - 3} }} + \sqrt x \) có nghĩa. A. \(x > 3\) B. \(x \ge 0\) C. \(x \ge 0\) và \(x \ne 3\) D. \(x \ne 3\) Câu 4. Cho \(P = \sqrt {53 - 20\sqrt 7 } = a + b\sqrt 7 \), với \(a,b\) là các số nguyên. Tính \(a - b\) A. 7 \(\) B. 73 C. –7 D. –3 Câu 5. Cho tam giác ABC vuông tại A và \(AB = 3,BC = 5\). Tính \(\tan \angle ACB\) A. \(\tan \angle ACB = \dfrac{5}{3}\) B. \(\tan \angle ACB = \dfrac{3}{5}\) C. \(\tan \angle ACB = \dfrac{4}{5}\) D. \(\tan \angle ACB = \dfrac{3}{4}\) Câu 6. Tìm thể tích V của khối hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là \(a,2a,3a\) A. \(V = 3{a^3}\) B. \(V = 6{a^3}\) C. \(V = {a^3}\) D. \(V = 2{a^3}\) Câu 7. Cho đường tròn \(\left( O \right)\) ngoại tiếp tam giác vuông cân có cạnh góc vuông bằng \(a\sqrt 2 \). Tính diện tích S của hình tròn \(\left( O \right)\) A. \(S = \dfrac{1}{2}\pi {a^2}\) B. \(S = 4\pi {a^2}\) C. \(S = \pi {a^2}\) D. \(S = 2\pi {a^2}\) Câu 8. Tính thể tích V của khối cầu có bán kính \(R = 2a\) A. \(V = \dfrac{4}{3}\pi {a^3}\) B. \(V = \dfrac{{32}}{3}\pi {a^3}\) C. \(V = 4\pi {a^3}\) D. \(V = 8\pi {a^3}\) B. Tự luận (8 điểm): Câu 1. (2,0 điểm) 1) Rút gọn biểu thức \(A = 7\sqrt {20} - 3\sqrt {25} \) 2) Tính giá trị của biểu thức \(B = \sqrt x + \dfrac{3}{{2\sqrt x }} + 4\) 3) Rút gọn biểu thức \(C = \dfrac{5}{{1 - \sqrt 2 }} - \dfrac{5}{{1 + \sqrt 2 }}\) Câu II. (2,0 điểm) 1) Giải phương trình \(2{x^2} - 6x + 1 = 0\) 2) Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 3\\x + 2y = 5\end{array} \right.\) Câu III. (1,5 điểm) Trong mặt phẳng Oxy, cho hàm số \(y = {x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(d:y = 2x - m + 1\)(với m là tham số) 1) Vẽ đồ thị \(\left( P \right)\) 2) Tìm tất cả các giá trị của tham số m để đường thẳng d cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt A và B có hoành độ lần lượt là \({x_1}\)và \({x_2}\) thỏa mãn điều kiện \(x_1^2 + x_2^2 = 2\left( {{x_1} + {x_2}} \right)\) Câu IV. (2,0 điểm) Cho đường tròn \(\left( O \right)\) có bán kính \(R = 2a\) và điểm A nằm ngoài đường tròn \(\left( O \right)\). Kẻ đến \(\left( O \right)\) hai tiếp tuyến AM và AN (với M, N là các tiếp điểm) 1) Chứng minh bốn diểm A, M, N, O cùng thuộc một đường tròn \(\left( C \right)\). Xác định tâm và bán kính của đường tròn \(\left( C \right)\). 2) Tính diện tích S của tứ giác AMON theo a, biết rằng \(OA = 3a\). 3) Gọi M’ là điểm đối xứng với M qua O và P là giao điểm của đường thẳng AO và\(\left( O \right)\), P nằm bên ngoài đoạn OA. Tính \(\sin \angle MPN.\) Câu V. (0,5 điểm) Cho x và y là hai số thực không âm thỏa mãn\(x + y = 4\). Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức \(P = {x^4} + {y^4} - 4xy + 3\). Lời giải A. Trắc nghiệm: (2,0 điểm)
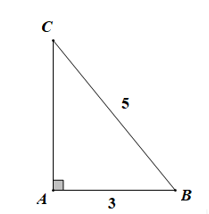
Câu 1 (NB): Phương pháp: Hàm số bậc nhất \(y = ax + b\) nghịch biến trên \(\mathbb{R}\) khi \(a < 0\) đồng biến khi \(a > 0\) Cách giải: Hàm số đã cho nghịch biến khi \(2 - m < 0 \Leftrightarrow m > 2\) Chọn D. Câu 2 (NB): Phương pháp: Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm trái dấu khi \(ac < 0\) Cách giải: Phương trình đã cho có \(ac = - 6 < 0\) nên có hai nghiệm trái dấu, nên nó có một nghiệm dương Chọn B. Câu 3 (TH): Phương pháp: Biểu thức có nghĩa khi các biểu thức trong căn không âm và biểu thức dưới mẫu khác 0 Cách giải: Biểu thức đã cho có nghĩa khi và chỉ khi \(\left\{ \begin{array}{l}x \ge 3\\\sqrt {x - 3} \ne 0\end{array} \right. \Leftrightarrow x > 3\) Chọn A. Câu 4 (TH): Phương pháp: Đưa biểu thức trong căn về bình phương Cách giải: Ta có \(P = \sqrt {53 - 20\sqrt 7 } = \sqrt {{5^2} - 2.5.2\sqrt 7 + {{\left( {2\sqrt 7 } \right)}^2}} \)\( = \sqrt {{{\left( {5 - 2\sqrt 7 } \right)}^2}} = \left| {5 - 2\sqrt 7 } \right| = 2\sqrt 7 - 5\) Vậy \(\left\{ \begin{array}{l}a = - 5\\b = 2\end{array} \right.\)\( \Rightarrow a - b = - 7\) Chọn C. Câu 5 (TH): Phương pháp: Áp dụng định lý Pitago, sau đó áp dụng công thức tan bằng đối trên kề Cách giải Áp dụng định lý Pitago vào tam giác vuông ABC ta có \(\begin{array}{l}AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{5^2} - {3^2}} = 4\\ \Rightarrow \tan \angle ACB = \dfrac{{AB}}{{AC}} = \dfrac{3}{4}\end{array}\) Chọn D.
Câu 6 (TH): Phương pháp: Thể tích khối hộp chữ nhật bằng tích ba kích thước của chúng Cách giải: Thể thích của khối hộp đã cho là \(V = a.2a.3a = 6{a^3}\) Chọn B. Câu 7 (VD): Phương pháp: Tính bán kính đường tròn, rồi áp dụng công thức diện tích Cách giải:
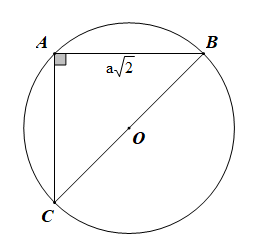
Giả sử tam giác ABC vuông cân tại A, nội tiếp đường tròn (O) Vì tam giác ABC vuông cân tại A nên đường tròn (O) có đường kính là \(BC = AB\sqrt 2 = a\sqrt 2 .\sqrt 2 = 2a\) Suy ra bán kính của (O) là \(r = a\) và diện tích là \(S = \pi {r^2} = \pi {a^2}\) Chọn C. Câu 8 (NB): Phương pháp: Áp dụng công thức thể tích khối cầu Cách giải:
Thể tích khối cầu đã cho là \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {\left( {2a} \right)^3} = \dfrac{{32}}{3}\pi {a^3}\) Chọn B. B. Tự luận: (8,0 điểm) Câu I (2,0 điểm): Phương pháp: 1) Sử dụng các công thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\) và \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,khi\,\,A < 0\end{array} \right.,\,\,B \ge 0.\) 2) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức. Cách giải: 1) Rút gọn biểu thức \(A = 7\sqrt {20} - 3\sqrt {25} \) Ta có: \(A = 7\sqrt {20} - 3\sqrt {25} \) \(\begin{array}{l} = 7\sqrt {4.5} - 3\sqrt {25} \\ = 7.\sqrt 4 .\sqrt 5 - 3.5\\ = 7.2.\sqrt 5 - 15\\ = 14\sqrt 5 - 15\end{array}\) Vậy \(A = 14\sqrt 5 - 15\) . 2) Tính giá trị của biểu thức \(B = \sqrt x + \dfrac{3}{{2\sqrt x }} + 4\) khi \(x = 9\) Điều kiện: \(x > 0\). Thay \(x = 9\) (thỏa mãn điều kiện) vào \(B = \sqrt x + \dfrac{3}{{2\sqrt x }} + 4\) ta được: \(\begin{array}{l}B = \sqrt 9 + \dfrac{3}{{2\sqrt 9 }} + 4\\ = 3 + \dfrac{3}{{2.3}} + 4\\ = 3 + \dfrac{1}{2} + 4 = \dfrac{{15}}{2}.\end{array}\) Vậy khi \(x = 9\) thì \(B = \dfrac{{15}}{2}\). 3) Rút gọn biểu thức \(C = \dfrac{5}{{1 - \sqrt 2 }} - \dfrac{5}{{1 + \sqrt 2 }}\) Ta có: \(C = \dfrac{5}{{1 - \sqrt 2 }} - \dfrac{5}{{1 + \sqrt 2 }}\)\( = \dfrac{{ - 5}}{{\sqrt 2 - 1}} - \dfrac{5}{{\sqrt 2 + 1}}\) \(\begin{array}{l} = \dfrac{{ - 5\left( {\sqrt 2 + 1} \right) - 5\left( {\sqrt 2 - 1} \right)}}{{\left( {\sqrt 2 - 1} \right)\left( {\sqrt 2 + 1} \right)}}\\ = \dfrac{{ - 5\sqrt 2 - 5 - 5\sqrt 2 + 5}}{{2 - 1}}\\ = \dfrac{{ - 10\sqrt 2 }}{1} = - 10\sqrt 2 \end{array}\) Vậy \(C = - 10\sqrt 2 \). Câu II (2,0 điểm) (VD): Phương pháp: 1) Tính biệt thức và áp dụng công thức nghiệm của phương trình bậc hai 2) Giải hệ phương trình bằng phương pháp cộng đại số Cách giải: 1) Giải phương trình \(2{x^2} - 6x + 1 = 0\). Ta có: \(\Delta ' = {3^2} - 2.1 = 7 > 0\) nên phương trình có hai nghiệm phân biệt \( \Leftrightarrow \left[ \begin{array}{l}{x_1} = \dfrac{{3 + \sqrt 7 }}{2}\\{x_2} = \dfrac{{3 - \sqrt 7 }}{2}\end{array} \right.\). Vậy tập nghiệm của phương trình là \(S = \left\{ {\dfrac{{3 \pm \sqrt 7 }}{2}} \right\}\). 2) Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 3\\x + 2y = 5\end{array} \right.\). \(\left\{ \begin{array}{l}2x - y = 3\\x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 2y = 6\\x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 11\\y = 2x - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{5}\\y = 2.\dfrac{{11}}{5} - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{5}\\y = \dfrac{7}{5}\end{array} \right.\). Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {\dfrac{{11}}{5};\dfrac{7}{5}} \right)\). Câu III (1,5 điểm) (VD): Phương pháp: 1) Lập bảng giá trị và vẽ đồ thị 2) Viết phương trình hoành độ giao điểm và hệ thức Vi–ét Cách giải: Trong mặt phẳng Oxy, cho hàm số \(y = {x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(d:\,\,y = 2x - m + 1\) (với \(m\) là tham số). 1) Vẽ đồ thị \(\left( P \right)\). + Ta có bảng giá trị:
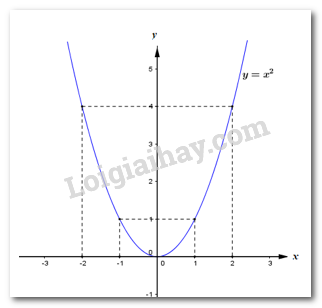
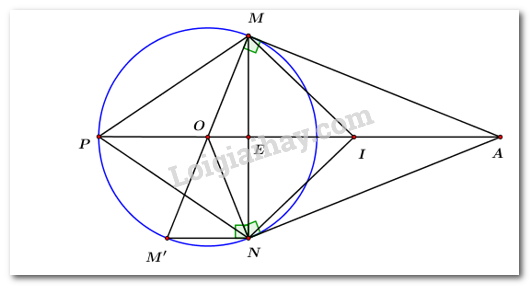
Do đó, parabol \(\left( P \right):\,\,y = {x^2}\) là đường cong đi qua các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) và nhận \(Oy\) là trục đối xứng. + Đồ thị hàm số: 2) Tìm tất cả các giá trị của tham số m để đường thẳng d cắt đồ thị (P) tại hai điểm phân biệt \(A\) và \(B\) có hoành độ lần lượt là \({x_1}\) và \({x_2}\) thỏa mãn điều kiện \(x_1^2 + x_2^2 = 2\left( {{x_1} + {x_2}} \right)\). Xét phương trình hoành độ giao điểm: \({x^2} = 2x - m + 1 \Leftrightarrow {x^2} - 2x + m - 1 = 0\) (*). Để đường thẳng \(\left( d \right)\) cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = 1 - m + 1 = 2 - m > 0 \Leftrightarrow m < 2\). Khi đó giả sử phương trình (*) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m - 1\end{array} \right.\). Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,\,x_1^2 + x_2^2 = 2\left( {{x_1} + {x_2}} \right)\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 2\left( {{x_1} + {x_2}} \right)\\ \Leftrightarrow {2^2} - 2\left( {m - 1} \right) = 2.2\\ \Leftrightarrow 4 - 2\left( {m - 1} \right) = 4\\ \Leftrightarrow 2\left( {m - 1} \right) = 0\\ \Leftrightarrow m - 1 = 0\\ \Leftrightarrow m = 1\,\,\,\left( {tm} \right)\end{array}\) Vậy \(m = 1\) thỏa mãn yêu cầu bài toán. Câu IV (2,0 điểm) – (VD): Cách giải: Cho đường tròn (O) có bán kính \(R = 2a\) và điểm A nằm ngoài đường tròn (O). Kẻ đến (O) hai tiếp tuyến AM và AN (với M, N là các tiếp điểm). 1) Chứng minh bốn điểm A, M, N, O cùng thuộc một đường tròn \(\left( C \right)\). Xác định tâm và bán kính của đường tròn \(\left( C \right)\). Gọi I là trung điểm của OA. Ta có: \(\angle OMA = {90^0}\) (AM là tiếp tuyến với \(\left( O \right)\)) \( \Rightarrow \Delta AMO\) vuông tại M Có MI là trung tuyến \( \Rightarrow MI = IO = IA\) (1) \(\angle ONA = {90^0}\) (AN là tiếp tuyến của \(\left( O \right)\)) \( \Rightarrow \Delta ANO\) vuông tại N Có NI là trung tuyến \( \Rightarrow NI = IO = IA\) (2) Từ (1) và (2) suy ra \(IO = IA = IM = IM\) nên 4 điểm A, M, N, O cùng thuộc đường tròn \(\left( C \right)\) tâm I bán kính \(R = \dfrac{{OA}}{2}\). (đpcm) 2) Tính diện tích S của tứ giác AMON theo \(a\), biết rằng \(OA = 3a\). Gọi E là giao điểm của MN là OA. Ta có: \(OM = ON = R\) và \(AM = AN\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow OA\) là đường trung trực của đoạn MN \( \Rightarrow OA \bot MN\) tại trung điểm E của MN. Tam giác OMA vuông tại M, theo Pitago ta có: \(A{M^2} = O{A^2} - O{M^2} = {\left( {3a} \right)^2} - {\left( {2a} \right)^2} = 5{a^2} \Rightarrow AM = a\sqrt 5 \) Tam giác \(AMO\) vuông tại M có ME là đường cao nên: \(ME.OA = OM.AM\) \( \Rightarrow ME = \dfrac{{OM.AM}}{{OA}} = \dfrac{{2a.a\sqrt 5 }}{{3a}} = \dfrac{{2a\sqrt 5 }}{3}\) \( \Rightarrow MN = 2ME = 2.\dfrac{{2a\sqrt 5 }}{3} = \dfrac{{4a\sqrt 5 }}{3}\) Tứ giác OMAN có hai đường chéo OA và MN vuông góc nên \({S_{OMAN}} = \dfrac{1}{2}OA.MN = \dfrac{1}{2}.3a.\dfrac{{4a\sqrt 5 }}{3} = 2{a^2}\sqrt 5 \). Vậy \({S_{OMAN}} = 2{a^2}\sqrt 5 \) 3) Gọi \(M'\) là điểm đối xứng với \(M\) qua \(O\) và \(P\) là giao điểm của đường thẳng \(AO\) và \(\left( O \right)\), \(P\) nằm bên ngoài đoạn \(OA.\) Tính \(\sin \angle MPN\). Nối M’ với N ta có \(\angle MPN = \angle MM'N\) (hai góc nội tiếp cùng chắn cung \(MN\)) \( \Rightarrow \sin \angle MPN = \sin \angle MM'N\) Tam giác MNM’ có \(\angle MNM' = {90^0}\) (góc nội tiếp chắn nửa đường tròn) nên là tam giác vuông tại N. \( \Rightarrow \sin \angle MM'N = \dfrac{{MN}}{{MM'}} = \dfrac{{4a\sqrt 5 }}{3}:4a = \dfrac{{\sqrt 5 }}{3}\) \( \Rightarrow \sin \angle MPN = \dfrac{{\sqrt 5 }}{3}\). Câu V (0,5 điểm) (VDC): Cách giải: Cho \(x\) và \(y\) là hai số thực không âm thỏa mãn \(x + y = 4\). Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức \(P = {x^4} + {y^4} - 4xy + 3\). Ta có: \(\begin{array}{l}P = {x^4} + {y^4} - 4xy + 3\\P = {\left( {{x^2} + {y^2}} \right)^2} - 2{\left( {xy} \right)^2} - 4xy + 3\\P = {\left[ {{{\left( {x + y} \right)}^2} - 2xy} \right]^2} - 2{\left( {xy} \right)^2} - 4xy + 3\\P = {\left( {x + y} \right)^4} - 4xy{\left( {x + y} \right)^2} + 4{\left( {xy} \right)^2} - 2{\left( {xy} \right)^2} - 4xy + 3\\P = 256 - 64xy + 2{\left( {xy} \right)^2} - 4xy + 3\\P = 2{\left( {xy} \right)^2} - 68xy + 259\end{array}\) Đặt \(t = xy\), áp dụng BĐT Cô-si ta có: \(0 \le xy \le {\left( {\dfrac{{x + y}}{2}} \right)^2} = 4\) \( \Rightarrow 0 \le t \le 4\). Khi đó ta có: \(\begin{array}{l}P = 2{t^2} - 68t + 259\\P = 2\left( {{t^2} - 34t + {{17}^2}} \right) - 319\\P = 2{\left( {t - 17} \right)^2} - 319\end{array}\) Với \(0 \le t \le 4 \Rightarrow - 17 \le t - 17 \le - 13\). \(\begin{array}{l} \Leftrightarrow {13^2} \le {\left( {t - 17} \right)^2} \le {17^2}\\ \Leftrightarrow {2.13^2} \le 2{\left( {t - 17} \right)^2} \le {2.17^2}\\ \Leftrightarrow {2.13^2} - 319 \le 2{\left( {t - 17} \right)^2} - 319 \le {2.17^2} - 319\\ \Leftrightarrow 19 \le P \le 259\end{array}\) Vậy \({P_{\min }} = 19 \Leftrightarrow t = 4 \Leftrightarrow \left\{ \begin{array}{l}xy = 4\\x + y = 4\end{array} \right.\). Khi đó \(x,\,\,y\) là nghiệm của phương trình \({X^2} - 4X + 4 = 0 \Leftrightarrow {\left( {X - 2} \right)^2} = 0 \Leftrightarrow X = 2\). \( \Rightarrow \left( {x;y} \right) = \left( {2;2} \right)\). \({P_{\max }} = 259 \Leftrightarrow t = 0 \Leftrightarrow \left\{ \begin{array}{l}xy = 0\\x + y = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0;\,\,y = 4\\y = 0;\,\,x = 4\end{array} \right. \Rightarrow \left( {x;y} \right) = \left( {0;4} \right)\) hoặc \(\left( {x;y} \right) = \left( {4;0} \right)\).
|




















Danh sách bình luận