Đề thi vào 10 môn Toán Cần Thơ năm 2019Tải vềA. PHẦN TRẮC NGHIỆM (4 điểm) Câu 1: Trên đường tròn Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
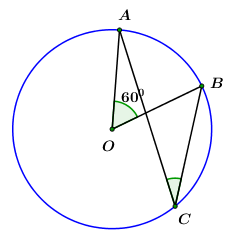
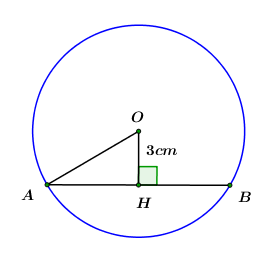
Đề bài A. PHẦN TRẮC NGHIỆM (4 điểm) Câu 1: Trên đường tròn \(\left( O \right)\) lấy các điểm phân biệt \(A,\,\,B,\,\,C\) sao cho \(\angle AOB = {60^0}\) (như hình vẽ).
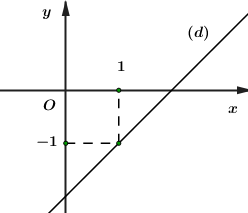
Số đo của \(\angle ACB\) bằng: A. \({30^0}\) B. \({60^0}\) C. \({15^0}\) D. \({120^0}\) Câu 2: Khẳng định nào dưới đây là sai? A. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ điểm đó qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến. B. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kinh đi qua các tiếp điểm. C. Trong một đường tròn, số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng số đo của cung bị chắn. D. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm. Câu 3: Bạn Nam trình bày lời giải hệ phương trình \(\left\{ \begin{array}{l}5x + 2y = - 4\\ - x + y = 5\end{array} \right.\) theo các bước sau: +) Bước 1: Hệ phương trình đã cho tương đương với:\(\left\{ \begin{array}{l}5x + 2y = - 4\\ - 5x + 5y = 25\end{array} \right..\) +) Bước 2: Cộng từng vế hai phương trình của hệ ta được: \(7y = 21.\) Suy ra \(y = 3.\) +) Bước 3: Thay \(y = 3\) vào phương trình thứ hai của hệ ta được \(x = - 2.\) +) Bước 4: Vậy nghiệm của hệ phương trình đã cho là:\(\left( { - 2;\,\,3} \right).\) Số bước giải đúng trong lời giải của Nam là: A. 2 B. 4 C. 3 D. 1 Câu 4: Diện tích của một hình tròn có bán kính bằng \(3\,cm\) là: A. \(18\pi \,\,c{m^2}\) B. \(6\pi \,\,c{m^2}\) C. \(3\pi \,\,c{m^2}\) D. \(9\pi \,\,c{m^2}\) Câu 5: Tập nghiệm của phương trình \({x^2} - x - 6 = 0\) là: A. \(\left\{ { - 3;\, - 2} \right\}\) B. \(\left\{ { - 3;\,\,2} \right\}\) C. \(\left\{ {2;\,\,3} \right\}\) D. \(\left\{ { - 2;\,\,3} \right\}\) Câu 6: Điểm nào sau đây là giao điểm của đường thẳng \(\left( d \right):\,\,y = - 2x - 3\) và parabol \(\left( P \right):\,\,y = - {x^2}?\) A. \(M\left( {3; - 9} \right)\) B. \(N\left( {1; - 1} \right)\) C. \(P\left( {3; - 6} \right)\) D. \(Q\left( { - 1;\,\,3} \right)\) Câu 7: Diện tích của một mặt cầu có bán kính bằng \(6\,cm\) là: A. \(288\pi \,\,c{m^2}\) B. \(96\pi \,\,c{m^2}\) C. \(48\pi \,\,c{m^2}\) D. \(144\pi \,\,c{m^2}\) Câu 8: Hàm số nào sau đây là hàm số bậc nhất? A. \(y = 2{x^2}\) B. \(y = \sqrt x + 1\) C. \(y = 1 - 2x\) D. \(y = - \dfrac{1}{x}\) Câu 9: Điều kiện của \(x\) để biểu thức \(\sqrt {3x - 6} \) có nghĩa là: A. \(x \ge - \dfrac{1}{2}\) B. \(x \ge 2\) C. \(x \ge - 2\) D. \(x \ge \dfrac{1}{2}\) Câu 10: Cho hàm số \(y = ax - 2\) có đồ thị là đường thẳng \(\left( d \right)\) như hình vẽ bên dưới.
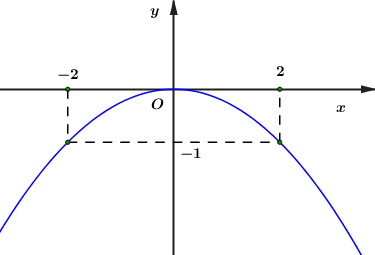
Hệ số góc của đường thẳng \(\left( d \right)\) bằng: A. \( - 1\) B. \(1\) C. \(2\) D. \( - 3\) Câu 11: Cho hàm số \(y = a{x^2}\) có đồ thị như hình vẽ bên.
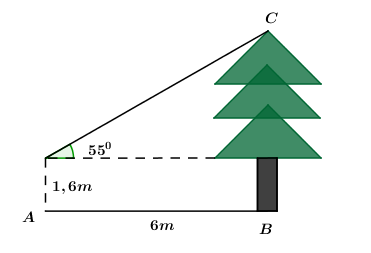
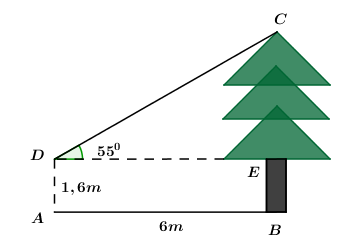
Hàm số đó là: A. \(y = \dfrac{1}{2}{x^2}\) B. \(y = - \dfrac{1}{2}{x^2}\) C. \(y = - \dfrac{1}{4}{x^2}\) D. \(y = \dfrac{1}{4}{x^2}\) Câu 12: Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \(2{x^2} - 6x - 5 = 0.\) Giá trị của biểu thức \(T = {x_1} + {x_2}\) bằng: A. \( - \dfrac{5}{2}\) B. \(3\) C. \( - 3\) D. \(\dfrac{5}{2}\) Câu 13: Cho đường thẳng \(d\) cắt đường tròn \(\left( O \right)\) tại hai điểm phân biệt \(A;\,\,B.\) Biết khoảng cách từ điểm \(O\) đến đường thẳng \(d\) bằng \(3cm\) và độ dài đoạn thẳng \(AB\) bằng \(8cm.\) Bán kính của đường tròn \(\left( O \right)\) bằng: A. \(7cm\) B. \(11cm\) C. \(73cm\) D. \(5cm\) Câu 14: Giá trị rút gọn của biểu thức \(P = \sqrt {125} + \sqrt {20} - \sqrt {80} \) bằng: A. \(11\sqrt 5 \) B. \(15\) C.\(3\sqrt 5 \) D. \(\sqrt {65} \) Câu 15: Nghiệm của hệ phương trình \(\left\{ \begin{array}{l} - 2x + 3y = 4\\3x - 2y = - 1\end{array} \right.\) là: A. \(\left( {1;\,2} \right)\) B. \(\left( { - 1;\, - 2} \right)\) C. \(\left( {2;\,\,1} \right)\) D. \(\left( { - 2; - 1} \right)\) Câu 16: Bạn Thanh đứng tại vị trí \(A\) cách cây thông \(6m\) và nhìn thấy ngọn của cây này dưới một góc bằng \({55^0}\) so với phương nằm ngang (như hình vẽ).
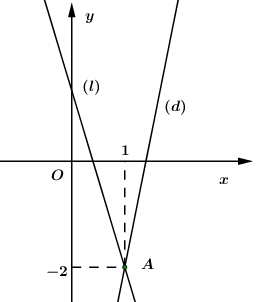
Biết khoảng cách từ mắt của bạn Thanh đến mặt đất bằng \(1,6m.\) Chiều cao \(BC\) của cây thông bằng (làm tròn đến số thập phân thứ hai): A. \(5,80m\) B. \(8,57m\) C. \(6,51m\) D. \(10,17m\) Câu 17: Cho điểm \(A\left( {a;\,\,b} \right)\) là giao điểm của hai đường thẳng \(\left( d \right)\) và \(\left( l \right)\) như hình vẽ:
Cặp số \(\left( {a;\,\,b} \right)\) là nghiệm của hệ phương trình nào sau đây? A. \(\left\{ \begin{array}{l}2x + y = - 5\\ - 4x + y = 9\end{array} \right.\) B. \(\left\{ \begin{array}{l}10x + 3y = 4\\ - 5x + y = - 7\end{array} \right.\) C. \(\left\{ \begin{array}{l}6x + 2y = - 2\\3x - y = 5\end{array} \right.\) D. \(\left\{ \begin{array}{l}2018x - y = 2020\\x + y = 3\end{array} \right.\) Câu 18: Bà Lan đến một cửa hàng bán trái cây để mua cam và quýt. Bà Lan trả cho cửa hàng hết 42 000 đồng khi mua 1 kg cam và 1 kg quýt. Người bán hàng cho biết tổng số tiền thu được khi bán 2 kg cam và 6 kg quýt bằng với tổng số tiền thu được khi bán 6 kg cam và 3 kg quýt. Giá bán của mỗi kg cam và mỗi kg quýt lần lượt là: A. 18 000 đồng và 24 000 đồng B. 20 000 đồng và 22 000 đồng C. 22 000 đồng và 20 000 đồng D. 24 000 đồng và 18 000 đồng Câu 19: Cho đường thẳng \(\left( {{d_1}} \right):\,\,y = ax + b\) song song với đường thẳng \(\left( {{d_2}} \right):\,\,\,y = 2x + 2019\) và cắt trục tung tại điểm \(A\left( {0; - 2} \right).\) Giá trị của biểu thức \({a^2} + {b^3}\) bằng: A. \( - 6\) B. \( - 2\) C. \( - 4\) D. \(12\) Câu 20: Một cái ly thủy tinh dạng hình trụ có diện tích đáy bằng \(50\,c{m^2}\) chứa \(500\,c{m^3}\) nước khoáng. Sau khi bé An uống nước trong ly thì người ta thấy mực nước trong ly giảm xuống \(3\,cm.\) Thể tích nước còn lại trong ly bằng: A. \(350\,c{m^3}\) B. \(150\,c{m^3}\) C. \(50\,c{m^3}\) D. \(450\,c{m^3}\) B. PHẦN TỰ LUẬN (6 điểm) Câu 1 (0,5 điểm): Vẽ đồ thị hà số \(y = - 2{x^2}.\) Câu 2 (1,5 điểm): Giải các phương trình và hệ phương trình sau: \(\begin{array}{l}a)\,\,{x^2} - x - 20 = 0\\b)\,\,\,\,\,4{x^4} - 5{x^2} - 9 = 0\end{array}\) \(c)\,\,\left\{ \begin{array}{l}2x - y = 8\\3x + 5y = - 1\end{array} \right..\) Câu 3 (1,5 điểm): a) Trong mặt phẳng tọa độ \(Oxy,\) cho parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,y = 2x + 4{m^2} - 8m + 3\) (\(m\) là tham số thực). Tìm các giá trị của \(m\) để \(\left( d \right)\) và \(\left( P \right)\) cắt nhau tại hai điểm phân biệt \(A\left( {{x_1};\,\,{y_1}} \right),\,\,B\left( {{x_2};\,\,{y_2}} \right)\) thỏa mãn điều kiện \({y_1} + {y_2} = 10.\) b) Trong kỳ thi Tuyển sinh vào lớp 10 THPT năm 2019, tổng chi tiêu tuyển sinh của Trường THPT A và Trường THPT B là 900 học sinh. Do cả hai trường đều có chất lượng giáo dục rất tốt nên sau khi hết thời gian điều chỉnh nguyện vọng thì số lượng thí sinh đăng ký dự tuyển vào trường THPT A và THPT B tăng lần lượt là 15% và 10% so với chỉ tiêu ban đầu. Vì vậy, tổng số thí sinh đăng ký dự tuyển của cả hai trường là 1010. Hỏi số lượng thí sinh đnagư ký dự tuyển của mỗi trường đăng là bao nhiêu? Câu 4 (2,5 điểm): Cho \(\Delta ABC\) nhọn \(\left( {AB > AC} \right)\) nội tiếp đường tròn tâm \(O.\) Các đường cao \(BE,\,\,CE\) cắt nhau tại \(H\,\,\left( {D \in AC,\,\,E \in AB} \right).\) Gọi \(M,\,\,N\) lân lượt là trung điểm của các cạnh \(AB\) và \(AC.\) a) Chứng minh các tứ giác \(BCDE\) và \(AMON\) nội tiếp. b) Chứng minh \(AE.AM = AD.AN.\) c) Gọi \(K\) là giao điểm của\(ED\) và \(MN,\,\,F\) là giao điểm của \(AO\) và \(MN,\,\,I\) là giao điểm của \(ED\) và \(AH.\) Chứng minh \(F\) là trực tâm \(\Delta KAI.\) Lời giải chi tiết I. PHẦN TRẮC NGHIỆM
Câu 1 Phương pháp Sử dụng định lý: Trong một đường tròn, góc ở nội tiếp bằng nửa số đo góc ở tâm cùng chắn một cung. Cách giải: Xét \(\left( O \right)\) có \(\angle AOB = {60^0}\) là góc ở tâm chắn cung \(AB,\,\,\angle ACB\) là góc nội tiếp chắn cung\(AB.\) \( \Rightarrow \angle ACB = \dfrac{1}{2}\angle AOB = {30^0}.\) Chọn A. Câu 2 Phương pháp Sử dụng tính chất của hai tiếp tuyến cắt nhau. Cách giải: Trong các đáp án đã cho, chỉ có đáp án C sai vì: “Trong một đường tròn, số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn”. Chọn C. Câu 3 Phương pháp Sử dụng phương pháp giải hệ phương trình bằng phương pháp thế. Cách giải: Các bước giải của bạn Nam đều đúng nên chọn đáp án B. Chọn B. Câu 4 Phương pháp Công thức tính diện tích hình tròn bán kính \(R\) là: \(S = \pi {R^2}.\) Cách giải: Ta có diện tích của hình tròn cần tính là: \(S = \pi {R^2} = 9\pi \,\,c{m^2}.\) Chọn D. Câu 5 Phương pháp Giải phương trình đã cho bằng công thức nghiệm hoặc đưa về phương trình tích hoặc bấm máy tính. Cách giải: \(\begin{array}{l}{x^2} - x - 6 = 0 \Leftrightarrow {x^2} - 3x + 2x - 6 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + 2\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 2\end{array} \right..\end{array}\) Vậy phương trình đã cho có tập nghiệm:\(S = \left\{ { - 2;\,\,3} \right\}.\) Chọn D. Câu 6 Phương pháp Xét phương trình hoành độ giao điểm của hai đồ thị hàm số sau, giải phương trình tìm hoành độ giao điểm. Thế hoành độ giao điểm vừa tìm được vào phương trình đường thẳng \(\left( d \right)\) hoặc \(\left( P \right)\) để tìm tung độ giao điểm. Cách giải: Phương trình hoành độ giao điểm của hai đồ thị hàm số là: \(\begin{array}{l} - {x^2} = - 2x - 3 \Leftrightarrow {x^2} - 2x - 3 = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right.\\ + )\,\,\,x = - 1 \Rightarrow y = - {\left( { - 1} \right)^2} = - 1\\ + )\,\,\,x = 3 \Rightarrow y = - {3^2} = - 9.\end{array}\) Vậy hai đồ thị hàm số cắt nhau tại hai điểm phân biệt \(\left( { - 1; - 1} \right)\) và \(\left( {3; - 9} \right).\) Chọn A. Câu 7 Phương pháp Diện tích mặt cầu bán kính \(R\) là: \(S = 4\pi {R^2}.\) Cách giải: Diện tích mặt cầu bài cho là: \(S = 4\pi {.6^2} = 144\,\pi \,\,c{m^2}.\) Chọn D. Câu 8 Phương pháp Hàm số \(y = ax + b\,\,\) là hàm số bậc nhất \( \Leftrightarrow a \ne 0.\) Cách giải: Trong các đáp án đã cho, chỉ có đáp án C có hàm số là hàm số bậc nhất. Chọn C. Câu 9 Phương pháp Biểu thức \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0.\) Cách giải: Biểu thức \(\sqrt {3x - 6} \) xác định \( \Leftrightarrow 3x - 6 \ge 0 \Leftrightarrow x \ge 2.\) Chọn B. Câu 10 Phương pháp Dựa vào đồ thị hàm số, xác định hệ số \(a.\) Đồ thị hàm số \(y = ax + b\) có hệ số góc là \(a.\) Cách giải: Dựa vào đồ thị hàm số ta thấy đồ thị hàm số đi qua điểm \(\left( {1; - 1} \right) \Rightarrow - 1 = a.1 - 2 \Leftrightarrow a = 1.\) Vậy hệ số góc của đường thẳng \(\left( d \right)\) là \(a = 1.\) Chọn B. Câu 11 Phương pháp Dựa vào đồ thị hàm số, nhận xét các điểm mà đồ thị hàm số đi qua. Thay tọa độ điểm mà đồ thị hàm số đi qua vào công thức hàm số để tìm \(a.\) Cách giải: Dựa vào đồ thị hàm số ta thấy đồ thị hàm số đi qua điểm \(\left( {2; - 1} \right)\)\( \Rightarrow - 1 = a{.2^2} \Leftrightarrow a = - \dfrac{1}{4}.\) \( \Rightarrow y = - \dfrac{1}{4}{x^2}.\) Chọn C. Câu 12 Phương pháp Áp dụng định lý Vi-et: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right..\) Cách giải: Ta có: \(2{x^2} - 6x - 5 = 0\) có \(a = 2;\,\,x = - 5 \Rightarrow ac < 0 \Rightarrow \) phương trình luôn có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\) Áp dụng hệ thức Vi-et ta có:\({x_1} + {x_2} = - \dfrac{b}{a} = \dfrac{6}{2} = 3.\) Chọn B. Câu 13 Phương pháp Đường thẳng \(d\) cắt \(\left( O \right)\) tại hai điểm \(A,\,\,B.\) Khi đó ta có: \(R = \sqrt {{d^2}\left( {O;\,\,AB} \right) + {{\left( {\dfrac{{AB}}{2}} \right)}^2}} .\) Cách giải:
Kẻ \(OH \bot AB.\) Khi đó ta có \(H\) là trung điểm của \(AB.\) (mối liên liên hệ giữa đường kính và dây cung) \( \Rightarrow \left\{ \begin{array}{l}OH = 3cm\\AH = \dfrac{1}{2}AB = 4cm\end{array} \right..\) Áp dụng định lý Pi-ta-go cho \(\Delta AOH\) vuông tại \(H\) ta có: \(\begin{array}{l}O{A^2} = A{H^2} + H{O^2} = {4^2} + {3^2} = 25\\ \Rightarrow R = OA = 5cm.\end{array}\) Chọn D. Câu 14 Phương pháp Sử dụng các công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,khi\,\,A < 0\end{array} \right..\) Cách giải: \(\begin{array}{l}P = \sqrt {125} + \sqrt {20} - \sqrt {80} = \sqrt {{5^2}.5} + \sqrt {{2^2}.5} - \sqrt {{4^2}.5} \\\,\,\,\,\, = 5\sqrt 5 + 2\sqrt 5 - 4\sqrt 5 = 3\sqrt 5 .\end{array}\) Chọn C. Câu 15 Phương pháp Giải hệ phương trình bằng phương pháp cộng đại số hoặc bấm máy tính. Cách giải: \(\begin{array}{l}\left\{ \begin{array}{l} - 2x + 3y = 4\\3x - 2y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6x + 9y = 12\\6x - 4y = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y = 10\\ - 2x + 3y = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 2\\ - 2x + 3.2 = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right..\end{array}\) Vậy nghiệm của hệ phương trình là: \(\left( {x;\,\,y} \right) = \left( {1;\,\,2} \right).\) Chọn A. Câu 16 Phương pháp Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để làm bài. Cách giải: Đặt các điểm \(D,\,\,E\) như hình vẽ.
Xét \(\Delta CDE\) vuông tại \(E\) ta có: \(CE = DE.\tan {55^0} = 6.\tan {55^0} \approx 8,57\,m.\) \( \Rightarrow \) Chiều cao của cây là: \(BC = CE + BE = 8,57 + 1,6 = 10,17\,\,m.\) Chọn D. Câu 17 Phương pháp Giao điểm của đường thẳng \(\left( d \right)\) và \(\left( l \right)\) là nghiệm của hệ phương trình gồm hai hàm số của \(\left( d \right)\) và \(\left( l \right).\) Giải hệ phương trình ở các đáp án để chọn đáp án đúng. Cách giải: Dựa vào đồ thị hàm số ta thấy đường thẳng \(\left( d \right)\) và \(\left( l \right)\) cắt nhau tại điểm \(\left( {1; - 2} \right)\) Khi đó \(\left( {a;\,\,b} \right) = \left( {1; - 2} \right).\) +) Xét đáp án A: \(\left\{ \begin{array}{l}2x + y = - 5\\ - 4x + y = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x = - 14\\y = - 5 - 2x\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{7}{3}\\y = - \dfrac{1}{3}\end{array} \right.\)\( \Rightarrow \) loại đáp án A. +) Xét đáp án B: \(\left\{ \begin{array}{l}10x + 3y = 4\\ - 5x + y = - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}10x + 3y = 4\\ - 10x + 2y = - 14\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}5y = - 10\\y = - 7 + 5x\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 2\end{array} \right.\)\( \Rightarrow \)Chọn B. Chọn B. Câu 18 Phương pháp Gọi giá tiền của \(1\,\,kg\) cam và \(1\,\,kg\) quýt lần lượt là: \(x,\,\,y\) đồng \(\left( {0 < \,x,\,\,y < 42\,\,000} \right).\) Dựa vào các giả thiết bài toán để lập hệ phương trình và giải bài toán bằng cách lập hệ phương trình. Giải hệ phương trình tìm \(x,\,\,y\) và đối chiếu với điều kiện rồi kết luận. Cách giải: Gọi giá tiền của \(1\,\,kg\) cam và \(1\,\,kg\) quýt lần lượt là: \(x,\,\,y\) đồng \(\left( {0 < \,x,\,\,y < 42\,\,000} \right).\) Khi bà Lan mua \(1\,\,kg\) cam và \(1\,\,kg\) quýt hết \(42\,000\) đồng nên ta có phương trình: \(x + y = 42\,000\,\,\,\,\,\left( 1 \right)\) Giá tiền khi bán \(2\,\,kg\) cam và \(6\,kg\) quýt bằng với giá \(6\,kg\) cam và \(3\,kg\) quýt nên ta có phương trình: \(2x + 6y = 6x + 3y \Leftrightarrow 4x - 3y = 0\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta hệ phương trình: \(\left\{ \begin{array}{l}x + y = 42\,\,000\\4x - 3y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 18\,000\,\,\,\left( {tm} \right)\\y = 24\,000\,\,\,\,\left( {tm} \right)\end{array} \right.\) Vậy giá bà Lan mua \(1\,kg\) cam là \(18\,000\) đồng và \(1\,\,kg\,\)quýt là \(24\,000\) đồng. Chọn A. Câu 19 Phương pháp Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right..\) Cách giải: Theo đề bài ta có:\({d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b \ne 2019\end{array} \right. \Rightarrow {d_1}:\,\,\,y = 2x + b.\) \({d_1}\) cắt trục tung tại \(A\left( {0; - 2} \right) \Rightarrow - 2 = 2.0 + b \Leftrightarrow b = - 2\,\,\left( {tm} \right)\) \( \Rightarrow {a^2} + {b^3} = {2^2} + {\left( { - 2} \right)^3} = 4 - 8 = - 4.\) Chọn C. Câu 20 Phương pháp Công thức tính thể tích hình trụ có chiều cao \(h\) và bán kính đáy \(R\) là: \(V = \pi {R^2}h.\) Công thức tính diện tích xung quanh hình trụ có chiều cao \(h\) và bán kính đáy \(R\) là: \({S_{xq}} = \pi Rh.\) Cách giải: Bán kính đáy của cốc nước là:\(R = \sqrt {\dfrac{{50}}{\pi }} \,\,cm \Rightarrow {R^2} = \dfrac{{50}}{\pi }.\) Chiều cao của cốc nước là: \(h = \dfrac{V}{{\pi {R^2}}} = \dfrac{{500}}{{\pi .\dfrac{{50}}{\pi }}} = 10\,\,cm.\) Chiều cao mức nước còn lại trong cốc sau khi bé An uống là: \(10 - 3 = 7\,cm.\) Thể tích nước bé An đã uống là: \(\pi {R^2}h' = \pi .\dfrac{{50}}{\pi }.7 = 350\,\,c{m^3}.\) Chọn A. II. PHẦN TỰ LUẬN Câu 1 (0,5 điểm): Cách giải: Vẽ đồ thị của hàm số \(y = - 2{x^2}\) Lập bảng giá trị:
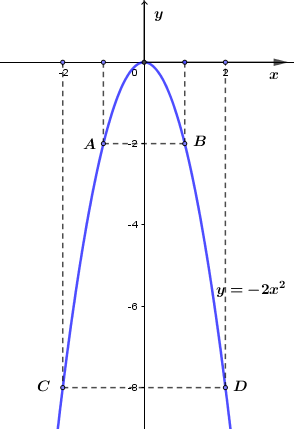
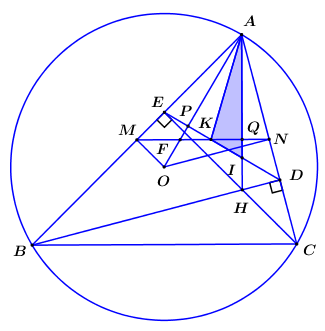
Đồ thị hàm số là đường cong parabol đi qua các điểm \(A\left( { - 1; - 2} \right);\,O\left( {0;0} \right);\,B\,\left( {1; - 2} \right);\,\,C\left( { - 2; - 8} \right) & ;\,\,D\left( {2; - 8} \right)\) và nhận trục Oy làm trục đối xứng. Đồ thị hàm số \(y = - 2{x^2}\) Câu 2 (1,5 điểm): Cách giải: \(\begin{array}{l}a)\,\,\,{x^2} - x - 20 = 0\\ \Leftrightarrow {x^2} - 5x + 4x - 20 = 0\\ \Leftrightarrow x\left( {x - 5} \right) + 4\left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {x + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\x + 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = - 4\end{array} \right.\end{array}\) Vậy tập nghiệm của phương trình là: \(S = \left\{ { - 4;5} \right\}\) \(b)\,\,\,4{x^4} - 5{x^2} - 9 = 0\) Đặt \({x^2} = t\,\,\left( {t \ge 0} \right)\). Khi đó phương trình trở thành: \(4{t^2} - 5t - 9 = 0\,\,\left( * \right)\). Ta có : \(a = 4;\,\,b = - 5;\,\,c = - 9 \Rightarrow a - b + c = 0\). Suy ra phương trình (*) có 2 nghiệm phân biệt ta có : \(\left[ \begin{array}{l}t = - 1\,\,\left( {ktm} \right)\\t = \dfrac{9}{4}\,\,\,\,\left( {tm} \right)\end{array} \right.\). Với \(t = \dfrac{9}{4} \Leftrightarrow {x^2} = \dfrac{9}{4} \Rightarrow x = \pm \dfrac{3}{2}\). Vậy tập nghiệm của phương trình là : \(S = \left\{ { - \dfrac{3}{2};\dfrac{3}{2}} \right\}\) \(c)\,\,\,\left\{ \begin{array}{l}2x - y = 8\\3x + 5y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}10x - 5y = 40\\3x + 5y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}13x = 39\\2x - y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 2\end{array} \right.\) Vậy nghiệm của hệ là : \(\left( {x;y} \right) = \left( {3; - 2} \right)\) Câu 3 (2,0 điểm): Cách giải: a) \(\left( P \right):\,\,y = {x^2};\,\,\left( d \right):\,\,y = 2x + 4{m^2} - 8m + 3\) Phương trình hoành độ giao điểm của (P) và (d) là : \({x^2} - 2x - 4{m^2} + 8m - 3 = 0\) (1) Số giao điểm của (d) và (P) cũng chính là số nghiệm của phương trình (1). Để (d) cắt (P) tại hai điểm phân biệt \(A\left( {{x_1};{y_1}} \right);\,\,B\left( {{x_2};{y_2}} \right)\) khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt \({x_1};\,\,{x_2}\). Ta có: \(\Delta ' = {\left( { - 1} \right)^2} + 4{m^2} - 8m + 3 = \,\,4{m^2} - 8m + 4 = \,\,4{\left( {m - 1} \right)^2}\) Phương trình (1) có 2 nghiệm phân biệt \({x_1};{x_2}\) khi và chỉ khi \(\Delta ' > 0 \Leftrightarrow 4{\left( {m - 1} \right)^2} > 0 \Leftrightarrow m \ne 1\) Áp dụng hệ thức Vi-et cho phương trình (1) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = - 4{m^2} + 8m - 3\end{array} \right.\) Theo đề bài ta có: \(\begin{array}{l}{y_1} + {y_2} = 10 \Leftrightarrow x_1^2 + x_2^2 = 10 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\\ \Leftrightarrow {2^2} - 2.\left( { - 4{m^2} + 8m - 3} \right) = 10 \Leftrightarrow 4 + 8{m^2} - 16m + 6 = 10\\ \Leftrightarrow 8{m^2} - 16m = 0 \Leftrightarrow 8m\left( {m - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\,\left( {tm} \right)\\m = 2\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy với \(m = 0;\,\,m = 2\) thỏa mãn yêu cầu bài toán. b) Gọi số lượng thí sinh đăng ký dự tuyển theo chỉ tiêu của trường THPT A là \(x\) (học sinh) \(\left( {x \in {N^*},x < 900} \right)\) Số lượng thí sinh đăng ký dự tuyển theo chỉ tiêu của trường THPT B là \(y\) (học sinh) \(\left( {y \in {N^*},y < 900} \right)\) Do tổng chi tiêu tuyển sinh của trường THPT A và THPT B là 900 học sinh nên ta có phương trình: \(x + y = 900\) (1) Sau khi hết thời gian điều chỉnh nguyện vọng thì số lượng thí sinh đăng ký dự tuyển vào trường THPT A là: \(115\% x\) (học sinh). Sau khi hết thời gian điều chỉnh nguyện vọng thì số lượng thí sinh đăng ký dự tuyển vào trường THPT B là: \(110\% x\) (học sinh). Khi đó tổng số học sinh đăng ký dự tuyển cả hai trường là 1010 học sinh nên ta có phương trình: \(115\% x + 110\% y = 1010\) (2) Từ (1) và (2) ta có hệ phương trình: \(\begin{array}{l}\,\,\,\,\,\,\left\{ \begin{array}{l}x + y = 900\\\dfrac{{115}}{{100}}x + \dfrac{{110}}{{100}}y = 1010\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 900\\115x + 110y = 101000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}110x + 110y = 99000\\115x + 110y = 101000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 2000\\x + y = 900\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 400\,\,\,\left( {tm} \right)\\y = 500\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy số lượng học sinh đăng ký dự tuyển vào trường THPT A là \(115\% .400 = 460\) học sinh; trường THPT B là \(1010 - 460 = 550\) học sinh. Câu 4 (2,5 điểm): Cho tam giác nhọn \(ABC\,\,\left( {AB > AC} \right)\) nội tiếp đường tròn tâm \(O\). Các đường cao \(BD\) và \(CE\) cắt nhau tại \(H\) (\(D\) thuộc \(AC,\,\,E\) thuộc \(AB\)). Gọi \(M,\,\,N\) lần lượt là trung điểm của cạnh \(AB\) và \(AC\). a) Chứng minh các tứ giác \(BCDE\) và \(AMON\) nội tiếp. b) Chứng minh \(AE.AM = AD.AN\). c) Gọi \(K\) là giao điểm của \(ED\) và \(MN,\,\,F\) là giao điểm của \(AO\) và \(MN\), \(I\) là giao điểm của \(ED\) và \(AH\). Chứng minh \(F\) là trực tâm tam giác \(KAI\). Cách giải: a) Chứng minh các tứ giác \(BCDE\) và \(AMON\) nội tiếp. Xét tứ giác \(BCDE\) có: \(\angle BEC = \angle BDC = {90^0}\,\,\left( {gt} \right) \Rightarrow \) Tứ giác \(BCDE\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau). Ta có: \(M\) là trung điểm của \(AB\,\,\left( {gt} \right) \Rightarrow OM \bot AB \Rightarrow \angle OMA = {90^0}\) (quan hệ vuông góc giữa đường kính và dây cung). Tương tự: \(N\) là trung điểm của \(AC\,\,\left( {gt} \right) \Rightarrow ON \bot AC \Rightarrow \angle ONA = {90^0}\) (quan hệ vuông góc giữa đường kính và dây cung). Xét tứ giác \(AMON\) có: \(\angle OMA + \angle ONA = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(OMAN\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800). b) Chứng minh \(AE.AM = AD.AN\). Tứ giác \(BCDE\) nội tiếp (cmt) \( \Rightarrow \angle AED = \angle ACB\) (góc ngoài và góc trong tại đỉnh đối diện). Dễ thấy \(MN\) là đường trung bình của tam giác \(ABC \Rightarrow MN//BC\). \( \Rightarrow \angle ACB = \angle ANM\) (đồng vị) \( \Rightarrow \angle AED = \angle ANM\,\,\left( { = & \angle ACB} \right)\). Xét tam giác \(AED\) và tam giác \(ANM\) có : \(\angle EAN\) chung ; \(\angle AED = \angle ANM\,\,\left( {cmt} \right);\) . c) Gọi \(K\) là giao điểm của \(ED\) và \(MN,\,\,F\) là giao điểm của \(AO\) và \(MN\), \(I\) là giao điểm của \(ED\) và \(AH\). Chứng minh \(F\) là trực tâm tam giác \(KAI\). Gọi \(P = OA \cap ED\) ; \(Q = MN \cap AH\). \(H = BD \cap CE \Rightarrow H\) là trực tâm của tam giác \(ABC \Rightarrow AH \bot BC\). Ta có \(MN//BC\,\,\left( {cmt} \right);\,\,AH \bot BC\,\,\left( {cmt} \right) \Rightarrow MN \bot AH\) tại \(Q\). Xét tam giác \(AMQ\) và tam giác \(AON\) có : \(\angle AMQ = \angle AMN = \angle AON\) (hai góc nội tiếp cùng chắn cung \(AN\)) \(\angle AQM = \angle ANO = {90^0}\) ; (hai góc tương ứng). \(\begin{array}{l} \Rightarrow \angle MAQ - \angle QAO = \angle OAN - \angle QAO\\ \Rightarrow \angle OAM = \angle QAN \Rightarrow \angle PAE = \angle QAN\end{array}\) Lại có \(\angle AED = \angle ANM\,\,\left( {cmt} \right) \Rightarrow \angle AEP = \angle ANQ\) \( \Rightarrow \angle PAE + \angle AEP = \angle QAN + \angle ANQ\). Xét tam giác vuông \(AQN\) có : \(\angle QAN + \angle ANQ = {90^0} \Rightarrow \angle PAE + \angle AEP = {90^0}\). \( \Rightarrow \Delta APE\) vuông tại \(P \Rightarrow AP \bot PE\) hay \(FA \bot KI\) (1). Ta đã chứng minh \(MN \bot AH \Rightarrow FQ \bot AI\) (2) Từ (1) và (2) \( \Rightarrow \) \(F\) là giao điểm của 2 đường cao \(FA,\,\,FQ\) của tam giác \(KAI\). Vậy \(F\) là trực tâm tam giác \(KAI\) (đpcm).
|




















Danh sách bình luận