Đề thi vào 10 môn Toán Bình Định năm 2020Tải vềBài 1: 1. Giải phương trình: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
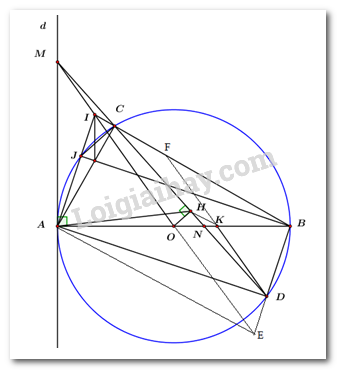
Đề bài Bài 1: 1. Giải phương trình: \(\dfrac{{x + 1}}{2} = x - 3\). 2. Cho biểu thức \(A = \left( {\dfrac{{\sqrt x + 2}}{{\sqrt x + 1}} - \dfrac{{2\sqrt x - 2}}{{\sqrt x - 1}}} \right).\left( {x - 1} \right)\), với \(x \ge 0,\,\,x \ne 1\). a) Tính giá trị biểu thức A khi \(x = 4\). b) Rút gọn biểu thức A và tìm giá trị lớn nhất của A. Bài 2: Cho Parabol \(\left( P \right):\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,y = 2\left( {m - 1} \right)x - 2m + 5\) (\(m\) là tham số). a) Chứng minh rằng đường thẳng \(\left( d \right)\) luôn cắt Parabol \(\left( P \right)\) tại hai điểm phân biệt với mọi giá trị của \(m.\) b) Tìm các giá trị của \(m\) để đường thẳng \(\left( d \right)\) cắt Parabol \(\left( P \right)\) tại hai điểm phân biệt có hoành độ tương ứng là \({x_1},\,\,{x_2}\) dương và \(\left| {\sqrt {{x_1}} - \sqrt {{x_2}} } \right| = 2.\) Bài 3: Trong kỳ thi chọn học sinh giỏi lớp 9 cấp trường, tổng số học sinh đạt giải của cả hai lớp 9A1 và 9A2 là 22 em, chiếm tỷ lệ 40% trên tổng số học sinh dự thi của hai lớp trên. Nếu tính riêng từng lớp thì lớp 9A1 có 50% học sinh dự thi đạt giải và lớp 9A2 có 28% học sinh dự thi đạt giải. Hỏi mỗi lớp có tất cả bao nhiêu học sinh dự thi. Bài 4: Cho đường tròn tâm \(O\), đường kính \(AB\) và \(d\) là một tiếp tuyến của đường tròn \(\left( O \right)\) tại điểm \(A\). Trên đường thẳng \(d\) lấy điểm \(M\) (khác \(A\)) và trên đoạn \(OB\) lấy điểm \(N\) (khác \(O\) và \(B\)). Đường thẳng \(MN\) cắt đường tròn \(\left( O \right)\) tại hai điểm \(C\) và \(D\) sao cho \(C\) nằm giữa \(M\) và \(D\). Gọi \(H\) là trung điểm của đoạn thẳng \(CD\). a) Chứng minh tứ giác \(AOHM\) nội tiếp được đường trong đường tròn. b) Kẻ đoạn \(DK//MO\) (\(K\) nằm trên đường thẳng \(AB\)). Chứng minh rằng \(\angle MDK = \angle BAH\) và \(M{A^2} = MC.MD.\) c) Đường thẳng \(BC\) cắt đường thẳng \(OM\) tại điểm \(I\). Chứng minh rằng đường thẳng \(AI\) song song với đường thẳng \(BD\). Bài 5: Cho \(x,\,\,y\) là các số thực dương thỏa mãn \(x + y = \sqrt {10} \). Tìm giá trị của \(x\) và \(y\) để biểu thức \(A = \left( {{x^4} + 1} \right)\left( {{y^4} + 1} \right)\) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó. Lời giải Bài 1 (2,0 điểm) Cách giải: 1. Giải phương trình: \(\dfrac{{x + 1}}{2} = x - 3\). \(\begin{array}{l}\,\,\,\,\,\,\dfrac{{x + 1}}{2} = x - 3\\ \Leftrightarrow x + 1 = 2x - 6\\ \Leftrightarrow 1 + 6 = 2x - x\\ \Leftrightarrow x = 7\end{array}\) Vậy nghiệm của phương trình là \(x = 7\). 2. Cho biểu thức \(A = \left( {\dfrac{{\sqrt x + 2}}{{\sqrt x + 1}} - \dfrac{{2\sqrt x - 2}}{{\sqrt x - 1}}} \right).\left( {x - 1} \right)\), với \(x \ge 0,\,\,x \ne 1\). a) Tính giá trị biểu thức A khi \(x = 4\). Thay \(x = 4\,\,\left( {TMDK} \right)\) vào biểu thức A ta có: \(\begin{array}{l}A = \left( {\dfrac{{\sqrt 4 + 2}}{{\sqrt 4 + 1}} - \dfrac{{2\sqrt 4 - 2}}{{\sqrt 4 - 1}}} \right).\left( {4 - 1} \right)\\A = \left( {\dfrac{4}{3} - \dfrac{2}{1}} \right).3\\A = \dfrac{{4 - 6}}{3}.3\\A = - 2\end{array}\) Vậy khi \(x = 4\) thì \(A = - 2\). b) Rút gọn biểu thức A và tìm giá trị lớn nhất của A. \(A = \left( {\dfrac{{\sqrt x + 2}}{{\sqrt x + 1}} - \dfrac{{2\sqrt x - 2}}{{\sqrt x - 1}}} \right).\left( {x - 1} \right)\) , với \(x \ge 0,\,\,x \ne 1\). \(\begin{array}{l} \Leftrightarrow A = \left( {\dfrac{{\sqrt x + 2}}{{\sqrt x + 1}} - \dfrac{{2\left( {\sqrt x - 1} \right)}}{{\sqrt x - 1}}} \right).\left( {x - 1} \right)\\ \Leftrightarrow A = \left( {\dfrac{{\sqrt x + 2}}{{\sqrt x + 1}} - 2} \right).\left( {x - 1} \right)\\ \Leftrightarrow A = \dfrac{{\sqrt x + 2 - 2\left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}.\left( {x - 1} \right)\\ \Leftrightarrow A = \dfrac{{\sqrt x + 2 - 2\sqrt x - 2}}{{\sqrt x + 1}}.\left( {\sqrt x + 1} \right).\left( {\sqrt x - 1} \right)\\ \Leftrightarrow A = - \sqrt x \left( {\sqrt x - 1} \right) = - x + \sqrt x \end{array}\) Ta có: \(A = - \left( {x - \sqrt x } \right)\) \(\begin{array}{l}A = - \left[ {{{\left( {\sqrt x } \right)}^2} - 2\sqrt x .\dfrac{1}{2} + {{\left( {\dfrac{1}{2}} \right)}^2}} \right] + \dfrac{1}{4}\\A = - {\left( {\sqrt x - \dfrac{1}{2}} \right)^2} + \dfrac{1}{4}\end{array}\) Vì \({\left( {\sqrt x - \dfrac{1}{2}} \right)^2} \ge 0\,\,\forall x \ge 0,\,\,x \ne 1\) nên \(A \le \dfrac{1}{4}\,\,\forall x \ge 0,\,\,x \ne 1\). Dấu “=” xảy ra \( \Leftrightarrow \sqrt x = \dfrac{1}{2} \Leftrightarrow x = \dfrac{1}{4}\,\,\left( {TM} \right)\). Vậy biểu thức A đạt giá trị lớn nhất bằng \(\dfrac{1}{4}\) khi và chỉ khi\(x = \dfrac{1}{4}\). Bài 2 (2,0 điểm) Cách giải: Cho Parabol \(\left( P \right):\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,y = 2\left( {m - 1} \right)x - 2m + 5\) (\(m\) là tham số). a) Chứng minh rằng đường thẳng \(\left( d \right)\) luôn cắt Parabol \(\left( P \right)\) tại hai điểm phân biệt với mọi giá trị của \(m.\) Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là: \({x^2} = 2\left( {m - 1} \right)x - 2m + 5\) \( \Leftrightarrow {x^2} - 2\left( {m - 1} \right)x + 2m - 5 = 0\,\,\,\left( * \right)\) Phương trình (*) có: \(\begin{array}{l}\Delta ' = {\left( {m - 1} \right)^2} - 2m + 5\\\,\,\,\,\,\, = {m^2} - 2m + 1 - 2m + 5\\\,\,\,\,\,\, = {m^2} - 4m + 4 + 2\\\,\,\,\,\,\, = {\left( {m - 2} \right)^2} + 2\end{array}\) Vì \({\left( {m - 2} \right)^2} \ge 0\,\,\forall m \Rightarrow {\left( {m - 2} \right)^2} + 2 > 0\,\,\forall m\). Do đó phương trình (*) luôn có hai nghiệm phân biệt với mọi giá trị của \(m\) hay đường thẳng \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt với mọi giá trị của \(m.\) b) Tìm các giá trị của \(m\) để đường thẳng \(\left( d \right)\) cắt Parabol \(\left( P \right)\) tại hai điểm phân biệt có hoành độ tương ứng là \({x_1},\,\,{x_2}\) dương và \(\left| {\sqrt {{x_1}} - \sqrt {{x_2}} } \right| = 2.\) Xét phương trình \({x^2} - 2\left( {m - 1} \right)x + 2m - 5 = 0\,\,\,\left( * \right)\) Để đường thẳng \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},\,\,{x_2}\) dương thì: \(\left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\,\,\forall m\\2\left( {m - 1} \right) > 0\\2m - 5 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 1\\m > \dfrac{5}{2}\end{array} \right. \Leftrightarrow m > \dfrac{5}{2}\). Khi đó với \({x_1},\,\,{x_2}\) là hai nghiệm phân biệt của phương trình \(\left( * \right)\), áp dụng hệ thức Vi-et cho phương trình \(\left( * \right)\) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right) = 2m - 2\\{x_1}{x_2} = 2m - 5\end{array} \right..\) Theo đề bài ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\left| {\sqrt {{x_1}} - \sqrt {{x_2}} } \right| = 2 \Leftrightarrow {\left( {\sqrt {{x_1}} - \sqrt {{x_2}} } \right)^2} = {2^2}\\ \Leftrightarrow {x_1} + {x_2} - 2\sqrt {{x_1}{x_2}} = 4 \Leftrightarrow 2m - 2 - 2\sqrt {2m - 5} = 4\\ \Leftrightarrow 2m - 6 = 2\sqrt {2m - 5} \Leftrightarrow m - 3 = \sqrt {2m - 5} \\ \Leftrightarrow \left\{ \begin{array}{l}m - 3 \ge 0\\{\left( {m - 3} \right)^2} = 2m - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge 3\\{m^2} - 6m + 9 = 2m - 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ge 3\\{m^2} - 8m + 14 = 0\,\,\,\left( 1 \right)\end{array} \right.\end{array}\) Giải phương trình \(\left( 1 \right)\) ta có: \(\Delta ' = {4^2} - 14 = 2 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}m = 4 + \sqrt 2 \,\,\,\left( {tm\,\,m \ge 3} \right)\\m = 4 - \sqrt 2 \,\,\,\left( {ktm\,\,\,m \ge 3} \right)\end{array} \right.\) (thỏa mãn điều kiện \(m > \dfrac{5}{2}\)). Vậy \(m = 4 + \sqrt 2 \) thỏa mãn bài toán. Bài 3 (1,5 điểm) Cách giải: Trong kỳ thi chọn học sinh giỏi lớp 9 cấp trường, tổng số học sinh đạt giải của cả hai lớp 9A1 và 9A2 là 22 em, chiếm tỷ lệ 40% trên tổng số học sinh dự thi của hai lớp trên. Nếu tính riêng từng lớp thì lớp 9A1 có 50% học sinh dự thi đạt giải và lớp 9A2 có 28% học sinh dự thi đạt giải. Hỏi mỗi lớp có tất cả bao nhiêu học sinh dự thi. Gọi số học sinh dự thi của lớp 9A1 và 9A2 lần lượt là \(x,\,\,y\) (học sinh) (ĐK:\(x,\,\,y \in {\mathbb{N}^*}\)). Vì số học sinh đạt giải là 22 em, chiếm tỷ lệ 40% trên tổng số học sinh dự thi của hai lớp trên nên ta có phương trình: \(\left( {x + y} \right).40\% = 22 \Leftrightarrow x + y = 55\,\,\,\left( 1 \right)\). Nếu tính riêng từng lớp thì: Lớp 9A1 có số học sinh đạt giải là \(50\% x = \dfrac{1}{2}x\) (học sinh). Lớp 9A2 có số học sinh đạt giải là \(28\% y = \dfrac{7}{{25}}y\) (học sinh). Vì cả hai lớp có 22 học sinh đạt giải nên ta có phương trình: \(\dfrac{1}{2}x + \dfrac{7}{{25}}y = 22 \Leftrightarrow 25x + 14y = 1100\,\,\,\left( 2 \right)\). Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 55\\25x + 14y = 1100\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25x + 25y = 1375\\25x + 14y = 1100\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}11y = 275\\x = 55 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 25\\x = 30\end{array} \right.\) (thỏa mãn). Vậy số học dự thi của lớp 9A1 là 30 học sinh, số học sinh dự thi của lớp 9A2 là 25 học sinh. Bài 4 (3,5 điểm) Cách giải: Cho đường tròn tâm \(O\), đường kính \(AB\) và \(d\) là một tiếp tuyến của đường tròn \(\left( O \right)\) tại điểm \(A\). Trên đường thẳng \(d\) lấy điểm \(M\) (khác \(A\)) và trên đoạn \(OB\) lấy điểm \(N\) (khác \(O\) và \(B\)). Đường thẳng \(MN\) cắt đường tròn \(\left( O \right)\) tại hai điểm \(C\) và \(D\) sao cho \(C\) nằm giữa \(M\) và \(D\). Gọi \(H\) là trung điểm của đoạn thẳng \(CD\).
a) Chứng minh tứ giác \(AOHM\) nội tiếp được đường trong đường tròn. Ta có: \(MA\) là tiếp tuyến của \(\left( O \right)\) \( \Rightarrow \angle MAO = {90^0}\) \(H\) là trung điểm của \(CD\) \( \Rightarrow OH \bot CD = \left\{ H \right\}\) (quan hệ giữa đường kính và dây cung) \( \Rightarrow \angle OHC = \angle OHM = {90^0}\) Xét tứ giác \(AOHM\) ta có: \(\angle MAO + \angle OHM = {90^0} + {90^0} = {180^0}\) Mà hai góc này là hai góc đối diện. \( \Rightarrow AOHM\) là tứ giác nội tiếp. (đpcm) b) Kẻ đoạn \(DK//MO\) (\(K\) nằm trên đường thẳng \(AB\)). Chứng minh rằng \(\angle MDK = \angle BAH\) và \(M{A^2} = MC.MD.\) Ta có: \(DK//MO\,\,\left( {gt} \right)\) \( \Rightarrow \angle MDK = \angle DMO\) (hai góc so le trong). Vì \(AOHM\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle HMO = \angle HAO\) (hai góc nội tiếp cùng chắn cung \(OH\)) Hay \(\angle BAH = \angle DMO\) \( \Rightarrow \angle BAH = \angle MDK\,\,\left( { = \angle DMO} \right)\) (đpcm). Xét \(\Delta AMC\) và \(\Delta DMA\) ta có: \(\angle M\,\,\,chung\) \(\angle MDA = \angle MAC\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AC\)) \(\begin{array}{l} \Rightarrow \Delta AMC \sim \Delta DMA\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{AM}}{{DM}} = \dfrac{{MC}}{{MA}} \Leftrightarrow M{A^2} = MC.MD\,\,\,\left( {cmt} \right).\end{array}\) c) Đường thẳng \(BC\) cắt đường thẳng \(OM\) tại điểm \(I\). Chứng minh rằng đường thẳng \(AI\) song song với đường thẳng \(BD\). Gọi \(E\) là giao điểm của \(MO\) và \(BD\). Kéo dài \(DK\) cắt \(BC\) tại \(F\). Xét tứ giác \(AHKD\) có \(\angle HAK = \angle KDH\) (câu b) \( \Rightarrow AHKD\) là tứ giác nội tiếp (hai đỉnh kề một cạnh cùng nhìn cạnh đối diện các góc bằng nhau) \( \Rightarrow \angle DAK = \angle DHK\) (góc nội tiếp cùng chắn cung \(DK\)) Mà \(\angle DAK = \angle DCB\) (góc nội tiếp cùng chắn cung \(DB\)) Nên \(\angle DHK = \angle DCB\) Hai góc này ở vị trí đồng vị nên \(HK//CB \Rightarrow HK//CF\). Trong tam giác \(DCF\), \(HK//CF,\) \(H\) là trung điểm của \(CD\) nên \(K\) là trung điểm của \(DF\). \( \Rightarrow DK = KF\) Lại có \(DK//MO \Rightarrow DF//IE\) \( \Rightarrow \dfrac{{DK}}{{OE}} = \dfrac{{FK}}{{OI}}\left( { = \dfrac{{BK}}{{BO}}} \right)\) Mà \(DK = FK\left( {cmt} \right)\) nên \(OE = OI\). Xét tứ giác \(AIBE\) có hai đường chéo \(IE\) và \(AB\) cắt nhau tại trung điểm \(O\) của mỗi đường nên \(AIBE\) là hình hình hành \( \Rightarrow AI//BE \Rightarrow AI//BD\) (đpcm). Bài 5 (1,0 điểm) Cách giải: Cho \(x,\,\,y\) là các số thực dương thỏa mãn \(x + y = \sqrt {10} \). Tìm giá trị của \(x\) và \(y\) để biểu thức \(A = \left( {{x^4} + 1} \right)\left( {{y^4} + 1} \right)\) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó. Ta có: \(\begin{array}{l}A = \left( {{x^4} + 1} \right)\left( {{y^4} + 1} \right)\\A = {x^4} + {y^4} + {\left( {xy} \right)^4} + 1\\A = {\left( {{x^2} + {y^2}} \right)^2} - 2{\left( {xy} \right)^2} + {\left( {xy} \right)^4} + 1\\A = {\left[ {{{\left( {x + y} \right)}^2} - 2xy} \right]^2} - 2{\left( {xy} \right)^2} + {\left( {xy} \right)^4} + 1\\A = {\left( {x + y} \right)^4} - 4{\left( {x + y} \right)^2}.xy + 4{\left( {xy} \right)^2} - 2{\left( {xy} \right)^2} + {\left( {xy} \right)^4} + 1\\A = 100 - 40.xy + 2{\left( {xy} \right)^2} + {\left( {xy} \right)^4} + 1\\A = {\left( {xy} \right)^4} + 2{\left( {xy} \right)^2} - 40xy + 101\end{array}\) Đặt \(t = xy\). Áp dụng BĐT Cô-si ta có: \(0 < xy \le {\left( {\dfrac{{x + y}}{2}} \right)^2} = \dfrac{{{{\left( {x + y} \right)}^2}}}{4} = \dfrac{5}{2}\). Khi đó ta có: \(A = {t^4} + 2{t^2} - 40t + 101\) với \(0 < t \le \dfrac{5}{2}\). \(\begin{array}{l}A = \left( {{t^4} - 8{t^2} + 16} \right) + \left( {10{t^2} - 40t + 40} \right) + 45\\A = {\left( {{t^2} - 4} \right)^2} + 10{\left( {t - 2} \right)^2} + 45 \ge 45\end{array}\) Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}{t^2} - 4 = 0\\t - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}t = 2\\t = - 2\end{array} \right.\\t = 2\end{array} \right. \Leftrightarrow t = 2\,\,\,\left( {tm} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}xy = 2\\x + y = \sqrt {10} \end{array} \right.\). Khi đó \(x,\,\,y\) là nghiệm của phương trình \({X^2} - \sqrt {10} X + 2 = 0\). Ta có: \(\Delta = {\left( {\sqrt {10} } \right)^2} - 4.1.2 = 2 > 0\), do đó phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}X = \dfrac{{\sqrt {10} - \sqrt 2 }}{2}\\X = \dfrac{{\sqrt {10} + \sqrt 2 }}{2}\end{array} \right.\). \( \Rightarrow \left( {x;y} \right) = \left( {\dfrac{{\sqrt {10} - \sqrt 2 }}{2};\dfrac{{\sqrt {10} + \sqrt 2 }}{2}} \right)\) hoặc \(\left( {x;y} \right) = \left( {\dfrac{{\sqrt {10} + \sqrt 2 }}{2};\dfrac{{\sqrt {10} - \sqrt 2 }}{2}} \right)\). Vậy biểu thức \({A_{\min }} = 45\) khi và chỉ khi \(\left( {x;y} \right) = \left( {\dfrac{{\sqrt {10} - \sqrt 2 }}{2};\dfrac{{\sqrt {10} + \sqrt 2 }}{2}} \right)\) hoặc \(\left( {x;y} \right) = \left( {\dfrac{{\sqrt {10} + \sqrt 2 }}{2};\dfrac{{\sqrt {10} - \sqrt 2 }}{2}} \right)\).
|




















Danh sách bình luận