Đề thi vào 10 môn Toán Bình Định năm 2021Tải vềBài 1 (2,0 điểm): 1. Cho biểu thức Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
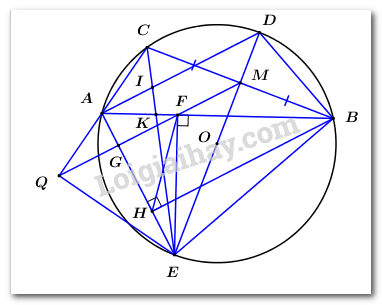
Đề bài Bài 1 (2,0 điểm): 1. Cho biểu thức: \(P = \left( {\dfrac{{\sqrt x }}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x + 1}}} \right):\left( {\dfrac{1}{{\sqrt x + 1}} + \dfrac{2}{{x - 1}}} \right)\) với \(x > 0,\,\,x \ne 1\). a) Rút gọn biểu thức \(P\). b) Tìm giá trị của \(P\) khi \(x = 4 - 2\sqrt 3 \). 2. Giải hệ phương trình: \(\left\{ \begin{array}{l}x + 2y = 6\\2x + 3y = 7\end{array} \right.\). Bài 2 (2,0 điểm): 1. Cho phương trình: \({x^2} - \left( {m + 3} \right)x - 2{m^2} + 3m = 0\) (\(m\) là tham số). hãy tìm giá trị của \(m\) để \(x = 3\) là nghiệm của phương trình và xác định nghiệm còn lại của phương trình( nếu có). 2. Cho Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = \left( {2m + 1} \right)x - 2m\) (\(m\) là tham số). Tìm \(m\) để \(\left( P \right)\) cắt \(\left( d \right)\) tại hai điểm phân biệt \(A( {{x_1};{y_1}}),\,\,B( {{x_2};{y_2}})\) sao cho \({y_1} + {y_2} - {x_1}{x_2} = 1\). Bài 3 (1,5 điểm): Một xe máy khởi hành tại địa điểm \(A\) đi đến địa điểm \(B\) cách \(A\) \(160km\), sau đó 1 giờ, môt ô tô đi từ \(B\) đến \(A\). Hai xe gặp nhau tại địa điểm \(C\) cách \(B\) \(72km\). Biết vận tốc của ô tô lớn hơn vận tốc của xe máy \(20km/h\). Tính vận tốc của mỗi xe. Bài 4 (3,5 điểm): Cho tam giác ABC có \(\angle ACB > {90^0}\) nội tiếp trong đường tròn tâm \(O\). Gọi \(M\) là trung điểm \(BC\), đường thẳng OM cắt cung nhỏ \(cung\,\,BC\) tại D, cắt cung lớn \(cung\,\,BC\) tại \(E\). Gọi \(F\) là chân đường vuông góc hạ từ E xuống AB, H là chân đường vuông góc hạ từ \(B\) xuống \(AE\). a) Chứng minh tứ giác \(BEHF\) là tứ giác nội tiếp. b) Chứng minh \(MF \bot AE\). c) Đường thẳng MF cắt AC tại Q. Đường thẳng EC cắt AD, AB lần lượt tại I và K. Chứng minh: \(\angle EQA = {90^0}\) và \(\dfrac{{EC}}{{IC}} = \dfrac{{EK}}{{IK}}\). Bài 5 (1,0 điểm): Cho \(a,\,\,b,\,\,c\) là các số dương thỏa \(\dfrac{1}{{1 + a}} + \dfrac{1}{{1 + b}} + \dfrac{1}{{1 + c}} = 2\). Chứng minh rằng \(abc \le \dfrac{1}{8}\). Lời giải Bài 1 Phương pháp: 1) a) Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)\) xác định mẫu thức chung của biểu thức Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức. b) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\), tìm được \(\sqrt x \) Thay vào \(P = \dfrac{{x + 1}}{{\sqrt x + 1}}\), ta tính được giá trị của \(P\)/ 2) Sử dụng phương pháp cộng đại số, tìm được nghiệm \(y\) Sử dụng phương pháp thế, tìm được nghiệm \(x\) Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình. Cách giải: 1) a) Với \(x > 0,\,\,x \ne 1\) ta có: \(\begin{array}{l}P = \left( {\dfrac{{\sqrt x }}{{\sqrt x - 1}} - \dfrac{1}{{\sqrt x + 1}}} \right):\left( {\dfrac{1}{{\sqrt x + 1}} + \dfrac{2}{{x - 1}}} \right)\\P = \dfrac{{\sqrt x \left( {\sqrt x + 1} \right) - \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}:\left( {\dfrac{1}{{\sqrt x + 1}} + \dfrac{2}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right)\\P = \dfrac{{x + \sqrt x - \sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}:\dfrac{{\sqrt x - 1 + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\P = \dfrac{{x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}.\dfrac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}\\P = \dfrac{{x + 1}}{{\sqrt x + 1}}\end{array}\) b) Ta có: \(x = 4 - 2\sqrt 3 = {\left( {\sqrt 3 } \right)^2} - 2\sqrt 3 + 1 = {\left( {\sqrt 3 - 1} \right)^2}\) (thỏa mãn ĐKXĐ). \( \Rightarrow \sqrt x = \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} = \sqrt 3 - 1\) (do \(\sqrt 3 - 1 > 0\)). Thay \(x = 4 - 2\sqrt 3 \) và \(\sqrt x = \sqrt 3 - 1\) vào biểu thức \(P\) sau khi rút gọn ta có: \(P = \dfrac{{4 - 2\sqrt 3 + 1}}{{\sqrt 3 - 1 + 1}} = \dfrac{{5 - 2\sqrt 3 }}{{\sqrt 3 }} = \dfrac{{5\sqrt 3 - 6}}{3}\). Vậy khi \(x = 4 - 2\sqrt 3 \) thì \(P = \dfrac{{5\sqrt 3 - 6}}{3}\). 2) Ta có: \(\left\{ \begin{array}{l}x + 2y = 6\\2x + 3y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 4y = 12\\2x + 3y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5\\x = 6 - 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5\\x = - 4\end{array} \right.\) Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( { - 4;5} \right)\). Bài 2 Phương pháp: 1) Thay \(x = 3\) vào phương trình, ta tìm được \(m\) Thay \(m\) vừa tìm được vào phương trình, ta tìm được nghiệm còn lại của phương trình. 2) Xét phương trình hoành độ giao điểm giữa \(\left( P \right)\) và \(\left( d \right)\) \(\left( 1 \right)\) Để \(\left( P \right)\) cắt \(\left( d \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\). \( \Leftrightarrow \Delta > 0\) Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(m\) Ta có \(A,\,\,B \in \left( P \right)\) nên \(\left\{ \begin{array}{l}{y_1} = x_1^2\\{y_2} = x_2^2\end{array} \right. \Rightarrow A\left( {{x_1};{x_1}^2} \right),\,\,B\left( {{x_2};{x_2}^2} \right)\). Thay \(m\) vào \({y_1} + {y_2} - {x_1}{x_2} = 1\), giải phương trình và tìm được \(m\). Cách giải: 1) Vì \(x = 3\) là nghiệm của phương trình nên ta có: \({3^2} - \left( {m + 3} \right)3 - 2{m^2} + 3m = 0\) \(\begin{array}{l} \Leftrightarrow 9 - 3m - 9 - 2{m^2} + 3m = 0\\ \Leftrightarrow 2{m^2} = 0 \Leftrightarrow m = 0\end{array}\) Thay \(m = 0\) vào phương trình ban đầu ta có: \({x^2} - 3x = 0 \Leftrightarrow x\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right.\). Vậy \(m = 0\) và phương trình có nghiệm khác là \(x = 0\). 2) Xét phương trình hoành độ giao điểm giữa \(\left( P \right)\) và \(\left( d \right)\) ta được: \({x^2} = \left( {2m + 1} \right)x - 2m \Leftrightarrow {x^2} - \left( {2m + 1} \right)x + 2m = 0\,\,\,\,\left( 1 \right)\) Để \(\left( P \right)\) cắt \(\left( d \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\)\( \Leftrightarrow \Delta > 0\) \(\begin{array}{l} \Leftrightarrow {\left( {2m + 1} \right)^2} - 8m > 0\\ \Leftrightarrow 4{m^2} + 4m + 1 - 8m > 0\\ \Leftrightarrow {\left( {2m - 1} \right)^2} > 0\\ \Leftrightarrow m \ne \dfrac{1}{2}\end{array}\) Khi đó áp dụng hệ thức Vi- ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = 2m\end{array} \right.\) Ta có \(A,\,\,B \in \left( P \right)\) nên \(\left\{ \begin{array}{l}{y_1} = x_1^2\\{y_2} = x_2^2\end{array} \right. \Rightarrow A\left( {{x_1};{x_1}^2} \right),\,\,B\left( {{x_2};{x_2}^2} \right)\). Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,\,\,{y_1} + {y_2} - {x_1}{x_2} = 1\\ \Leftrightarrow {x_1}^2 + {x_2}^2 - {x_1}{x_2} = 1\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2} = 1\\ \Leftrightarrow {\left( {2m + 1} \right)^2} - 6m = 1\\ \Leftrightarrow 4{m^2} + 4m + 1 - 6m - 1 = 0\\ \Leftrightarrow 4{m^2} - 2m = 0\\ \Leftrightarrow 2m\left( {2m - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\,\,\,\left( {tm} \right)\\m = \dfrac{1}{2}\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy \(m = 0\). Bài 3 Phương pháp: Gọi vận tốc của xe máy là \(x\,\,\,\left( {km/h} \right)\)(\(x > 0\)) Tính được vận tốc của ô tô theo \(x\) Tính được thời gian xe máy đi từ A đến C và thời gian ô tô đi từ B đến C theo \(x\) Dựa vào giả thiết thời gian đi của xe máy và ô tô, lập được phương trình Giải phương trình, đối chiếu điều kiện và kết luận. Cách giải: Gọi vận tốc của xe máy là \(x\,\,\,\left( {km/h} \right)\)(\(x > 0\)) \( \Rightarrow \) Vận tốc của ô tô là \(x + 20\,\,\left( {km/h} \right)\) Quãng đường AC là: \(160 - 72 = 88\,\,\left( {km} \right)\) Thời gian xe máy đi từ A đến C là: \(\dfrac{{88}}{x}\left( h \right)\) Thời gian ô tô đi từ B đến C là: \(\dfrac{{72}}{{x + 20}}\left( h \right)\) Vì ô tô đi muộn hơn xe máy 1 giờ nên thời gian ô tô đi từ B đến C ít hơn thời gian đi từ A đến C là 1 giờ, ta có phương trình: \(\dfrac{{88}}{x} - \dfrac{{72}}{{x + 20}} = 1\) \(\begin{array}{l} \Leftrightarrow \dfrac{{88\left( {x + 20} \right) - 72x}}{{x\left( {x + 20} \right)}} = \dfrac{{x\left( {x + 20} \right)}}{{x\left( {x + 20} \right)}}\\ \Rightarrow 16x + 1760 = {x^2} + 20x\\ \Leftrightarrow {x^2} + 4x - 1760 = 0\left( 1 \right)\end{array}\) Ta có: \(\Delta ' = {2^2} + 1760 = 1764 = {42^2} > 0\) nên phương trình (1) có 2 nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - 2 + 42}}{1} = 40\,\,\,\,\left( {tm} \right)\\{x_2} = \dfrac{{ - 2 - 42}}{1} = - 44\,\,\left( {ktm} \right)\end{array} \right.\) Vậy vận tốc của xe máy là \(40km/h\) và của ô tô là \(40 + 20 = 60km/h\). Bài 4 Phương pháp: a) Vận dụng dấu hiệu nhận biết: Tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau là tứ giác nội tiếp. b) Ta sẽ chứng minh: + 5 điểm \(B,\,\,M,\,\,F,\,\,H,\,\,E\) cùng thuộc đường tròn đường kính \(BE\). + \(\angle MFB = \angle FBH\) Suy ra \(MF//BH\) mà \(BH \bot AE\,\,\left( {gt} \right)\) nên \(MF \bot AE\,\,\left( {dpcm} \right)\) (quan hệ từ vuông góc đên song song) c) Ta sẽ chứng minh: + \(\Delta FAQ\) cân tại A \( \Rightarrow AQ\, = AF\) + \(\Delta AEQ\)\( = \,\Delta AEF\)(c.g.c) Suy ra \(\angle EQA = \angle EFA = {90^0}\) (2 góc tương ứng) Sử dụng tích chất đường phân trong và đường phân giác ngoài của góc ở đỉnh \(A\) Cách giải:
a) Ta có: \(\angle BFE = {90^0}\) (vì \(EF \bot AB\)); \(\angle BHE = {90^0}\) (vì \(BH \bot AE\)). \( \Rightarrow \) 4 điểm \(B,\,\,F,\,\,H,\,\,E\) cùng thuộc một đường tròn đường kính \(BE\). \( \Rightarrow \) Tứ giác \(BEHF\) nội tiếp (đpcm) b) Ta có: \(M\) là trung điểm \(BC\) nên \(OM \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow \angle OMB = {90^0}\) Mà \(\angle BFE = {90^0}\) (vì \(EF \bot AB\)) Suy ra 4 điểm \(B,\,\,M,\,\,E,\,\,F\) cùng thuộc đường tròn đường kính \(BE\). \( \Rightarrow \) 5 điểm \(B,\,\,M,\,\,F,\,\,H,\,\,E\) cùng thuộc đường tròn đường kính \(BE\). Ta có: \(\angle MFB = \angle MEB\) (2 góc nội tiếp cùng chắn cung \(BM\)). \(\angle FBH = \angle FEH\) (2 góc nội tiếp cùng chắn cung \(HF\)). Ta lại có: \(\angle MEB + \angle BDE = {90^0}\) (tam giác \(BDE\) vuông tại \(B\) do có \(\angle DBE = {90^0}\) - góc nội tiếp chắn nửa đường tròn). \(\angle FEH + \angle BAE = {90^0}\) (do tam giác \(AEF\) vuông tại \(F\)) Mà \(\angle BAE = \angle BDE\) (2 góc nội tiếp cùng chắn cung \(BE\)) nên \(\angle MEB = \angle FEH\). \( \Rightarrow \angle MFB = \angle FBH\). Mà hai góc này ở vị trí so le trong nên \(MF//BH\). Lại có \(BH \bot AE\,\,\left( {gt} \right)\). Vậy \(MF \bot AE\,\,\left( {dpcm} \right)\). c) \(\angle EQA = {90^0}\) và \(\dfrac{{EC}}{{IC}} = \dfrac{{EK}}{{IK}}\). Do \(OD\) là bán kính đi qua trung điểm dây cung \(BC\) nên \(D\) là điểm chính giữa cung nhỏ \(BC\). \( \Rightarrow \)sđ \(cung\,BD = \)sđ \(cung\,DC = \dfrac{1}{2}\)sđ \(cung\,BC\) \( \Rightarrow \angle BAD = \angle CAD\) (Các góc nội tiếp chắn các cung bằng nhau) Suy ra \(AD\) là phân giác trong góc \(BAC\). Mà \(\angle EAD = {90^0}\)(góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AE \bot AD\). Suy ra \(AE\) là phân giác góc ngoài của góc \(BAC\) nên \(AE\) là phân giác \(\angle FAQ\) (do \(\angle FAQ\) và \(\angle BAC\) kề bù) (1) Mà \(AE\) cũng là đường cao của \(\Delta FAQ\) (do\(AE \bot MF\) tại \(G\)) ( chứng minh ý b)) (2) Từ (1) và (2) suy ra \(\Delta FAQ\) cân tại A \( \Rightarrow AQ\, = AF\) (tính chất tam giác cân). Xét \(\Delta AQE\) và \(\Delta AFE\)ta có: \(AE\) là cạnh chung \(\angle EAQ = \angle EAF\) (trong tam giác cân, đường cao đồng thời là phân giác). \(AQ\, = AF\,\,\left( {cmt} \right)\) Do đó \(\Delta AEQ\)\( = \,\Delta AEF\)(c.g.c) Suy ra \(\angle EQA = \angle EFA = {90^0}\) (2 góc tương ứng) (đpcm). Xét tam giác \(KAC\) có \(AI\,,\,AE\) lần lượt là phân giác trong, phân giác ngoài của góc ở đỉnh \(A\). Theo tính chất đường phân giác ta có: \(\dfrac{{EC}}{{EK}} = \dfrac{{IC}}{{IK}}\)(cùng bằng \(\dfrac{{AC}}{{AK}}\)) Vậy \(\dfrac{{EC}}{{IC}} = \dfrac{{EK}}{{IK}}\,\,\left( {dpcm} \right)\). Bài 5 Phương pháp: Sử dụng bất đẳng thức Cô – si để chứng minh. Cách giải: Ta có: \(\begin{array}{l}\dfrac{1}{{1 + a}} + \dfrac{1}{{1 + b}} + \dfrac{1}{{1 + c}} = 2\\ \Rightarrow \dfrac{1}{{1 + a}} = 2 - \dfrac{1}{{1 + b}} - \dfrac{1}{{1 + c}} = 1 - \dfrac{1}{{1 + b}} + 1 - \dfrac{1}{{1 + c}}\\ \Rightarrow \dfrac{1}{{1 + a}} = 2 - \dfrac{1}{{1 + b}} - \dfrac{1}{{1 + c}} = \dfrac{b}{{1 + b}} + \dfrac{c}{{1 + c}}\end{array}\) Áp dụng BĐT Cô-si ta có: \(\dfrac{1}{{1 + a}} = \dfrac{b}{{1 + b}} + \dfrac{c}{{1 + c}} \ge 2\sqrt {\dfrac{{bc}}{{\left( {1 + b} \right)\left( {1 + c} \right)}}} \) Chứng minh tương tự ta có: \(\dfrac{1}{{1 + b}} \ge 2\sqrt {\dfrac{{ca}}{{\left( {1 + c} \right)\left( {1 + a} \right)}}} ,\,\,\dfrac{1}{{1 + c}} \ge 2\sqrt {\dfrac{{ab}}{{\left( {1 + a} \right)\left( {1 + b} \right)}}} \). Nhân vế theo vế của 3 BĐT trên ta có: \(\begin{array}{l}\dfrac{1}{{1 + a}}.\dfrac{1}{{1 + b}}.\dfrac{1}{{1 + c}} \ge 8\sqrt {\dfrac{{{a^2}{b^2}{c^2}}}{{{{\left( {1 + a} \right)}^2}{{\left( {1 + b} \right)}^2}{{\left( {1 + c} \right)}^2}}}} = \dfrac{{8abc}}{{\left( {1 + a} \right)\left( {1 + b} \right)\left( {1 + c} \right)}}\\ \Leftrightarrow 1 \ge 8abc \Leftrightarrow abc \le \dfrac{1}{8}\,\,\,\left( {dpcm} \right)\end{array}\) Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}a = b = c\\\dfrac{1}{{1 + a}} + \dfrac{1}{{1 + b}} + \dfrac{1}{{1 + c}} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = b = c\\\dfrac{3}{{1 + a}} = 2\end{array} \right. \Leftrightarrow a = b = c = \dfrac{1}{2}\).
|




















Danh sách bình luận