Đề thi vào 10 môn Toán Bắc Giang năm 2019

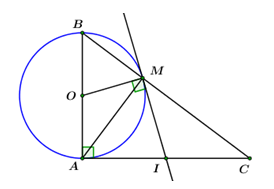
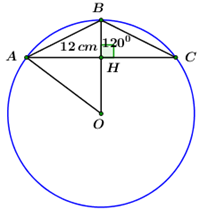
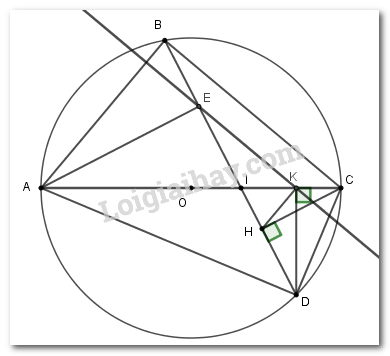
Đề bài

PHẦN I. TRẮC NGHIỆM (3 điểm)

Câu 1: Với \(x < 2\) thì biểu thức \(\sqrt {{{\left( {2 - x} \right)}^2}}  + x - 3\) có giá trị bằng

A.  \( - 1\)

B.  \(2x - 5\)  

C. \(5 - 2x\) 

D.  \(1\)

Câu 2: Giá trị của biểu thức \(\dfrac{{3 + \sqrt 3 }}{{\sqrt 3  + 1}}\) bằng:

A. \(\dfrac{1}{3}\)                                          B.   \(\sqrt 3 \)                                     C. \(3\)                                                D. \(\dfrac{1}{{\sqrt 3 }}\)  

Câu 3: Đường thẳng \(y = 4x - 5\) có hệ số góc bằng

A. \(5\)    

B.  \( - 5\)   

C. \( - 4\) 

D.  \(4\)  

Câu 4: Giá trị của tham số \(m\) để đường thẳng \(y = mx + 1\) song song với đường thẳng \(y = 2x - 3\) là:

A.  \(m =  - 1\)   

B.  \(m =  - 3\)   

C. \(m = 2\)   

D.  \(m = 1\)  

Câu 5: Căn bậc hai số học của \(144\) là:

A. \(12\)      

B. \(13\)     

C. \( - 12\)   

D.  \(12\) và \( - 12\)

Câu 6: Giá trị của tham số \(m\) để đường thẳng \(y = \left( {2m + 1} \right)x + 3\) đi qua điểm \(A\left( { - 1;\,\,0} \right)\) là:

A. \(m =  - 2\)    

B. \(m =  - 1\)    

C.  \(m = 2\)   

D. \(m = 1\)   

Câu 7: Tất cả các giá trị của \(x\) để biểu thức \(\sqrt {x - 3} \) có nghĩa là:

A. \(x < 3\)                              B. \(x \le 3\)                             C. \(x > 3\)                              D. \(x \ge 3\)

Câu 8: Giá trị nào của \(x\) dưới đây là nghiệm của phương trình \({x^2} + x - 2 = 0?\)  

A. \(x = 2\)                              B. \(x = 3\)                              C. \(x = 1\)                              D. \(x = 4\)

Câu 9: Cho \(\Delta ABC\) có \(AB = 3cm,\,\,AC = 4cm,\,\,BC = 5cm.\) Phát biểu nào dưới đây đúng?

A. Tam giác \(ABC\) vuông.                                      B. Tam giác \(ABC\) cân.                              

C. Tam giác \(ABC\) đều.                                          D. Tam giác \(ABC\) vuông cân.

Câu 10: Cho biết \(x = 1\) là một nghiệm của phương trình \({x^2} + bx + c = 0.\) Khi đó ta có:

A. \(b + c = 1.\)                                   B. \(b + c =  - 1.\)                    C. \(b + c = 2.\)                                   D. \(b + c = 0.\)

Câu 11: Hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\x + 2y = 7\end{array} \right.\) có nghiệm là \(\left( {{x_0};\,\,{y_0}} \right).\) Giá trị của biểu thức \({x_0} + {y_0}\) bằng:

A. \(1\)                                                B. \(4\)                                                 C. \(5\)                                                D. \( - 2\)  

Câu 12: Tổng hai nghiệm của phương trình \({x^2} - 4x + 3 = 0\) bằng:

A. \( - 4\)                                             B. \( - 3\)                                 C. \(3\)                                                D. \(4\)  

Câu 13: Cho tam giác \(ABC\) vuông tại \(A,\,\,\,BC = 4cm,\,\,\,AC = 2cm.\) Tính \(\sin \angle ABC.\)  

A. \(\dfrac{{\sqrt 3 }}{2}\)                             B. \(\dfrac{1}{2}\)                                          C. \(\dfrac{1}{2}\)                                                  D. \(\dfrac{1}{3}\)    

Câu 14: Hệ phương trình \(\left\{ \begin{array}{l}x + y = 3\\mx - y = 3\end{array} \right.\) có nghiệm là \(\left( {{x_0};\,\,{y_0}} \right)\) thỏa mãn \({x_0} = 2{y_0}.\) Khi đó giá trị của \(m\) là:

A. \(m = 4\)                             B. \(m = 2\)                             C. \(m = 5\)                             D. \(m = 3\)    

Câu 15: Biết rằng đường thẳng \(y = 2x + 3\) cắt parabol \(y = {x^2}\) tại hai điểm. Tọa độ các giao điểm là:

A. \(\left( { - 1;\,\,1} \right)\) và \(\left( {3;\,\,9} \right)\)                 B. \(\left( {1;\,\,1} \right)\) và \(\left( { - 3;\,\,9} \right)\)                       C. \(\left( { - 1;\,\,1} \right)\) và \(\left( { - 3;\,\,9} \right)\)              D. \(\left( {1;\,\,1} \right)\) và \(\left( {3;\,\,9} \right)\) 

Câu 16: Cho đường tròn \(\left( {O;\,\,R} \right)\) và dây cung \(AB\) thỏa mãn \(\angle AOB = {90^0}.\) Độ dài cung nhỏ \(AB\) bằng:

A. \(\pi R\)                              B. \(\dfrac{{3\pi R}}{2}\)                              C. \(\dfrac{{\pi R}}{4}\)                                D. \(\dfrac{{\pi R}}{2}\)   

Câu 17: Cho \(\Delta ABC\) vuông tại \(A,\,\,\,AC = 20cm.\) Đường tròn đường kính \(AB\) cắt \(BC\) tại \(M\,\,\,\left( {M \ne B} \right),\) tiếp tuyến tại \(M\) của đường tròn đường kính \(AB\) cắt \(AC\) tại \(I.\) Độ dài đoạn thẳng \(AI\) bằng:

A. \(10cm\)                             B. \(12cm\)                             C. \(6cm\)                               D. \(9cm\)  

Câu 18: Tam giác \(ABC\) cân tại \(B\) có \(\angle ABC = {120^0},\,\,AB = 12cm\) và nội tiếp đường tròn \(\left( O \right).\) Bán kính của đường tròn \(\left( O \right)\) bằng:

A. \(10cm\)                             B. \(12cm\)                             C. \(8cm\)                               D. \(9cm\)  

Câu 19: Tìm tham số \(m\) để phương trình \({x^2} + x + m + 1 = 0\) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 5.\)  

A. \(m = 2\)                                         B. \(m = 0\)                             C. \(m =  - 3\)                         D. \(m = 1\)  

Câu 20: Cho hàm số \(y = f\left( x \right) = \left( {1 + {m^4}} \right)x + 1,\) với \(m\) là tham số. Khẳng định nào sau đây đúng?

A. \(f\left( 4 \right) < f\left( 2 \right)\)                      B. \(f\left( { - 1} \right) > f\left( 0 \right)\)               C. \(f\left( 2 \right) < f\left( 3 \right)\)              D. \(f\left( 1 \right) > f\left( 2 \right)\)  

PHẦN II. TỰ LUẬN (7 điểm)

Câu 1 (2 điểm)

a) Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 2\\3x + 2y = 11\end{array} \right..\)

b) Rút gọn biểu thức \(A = \left[ {\dfrac{{2\left( {x - 2\sqrt x  + 1} \right)}}{{x - 4}} - \dfrac{{2\sqrt x  - 1}}{{\sqrt x  + 2}}} \right]:\dfrac{{\sqrt x }}{{\sqrt x  - 2}}\) với \(x > 0,\,\,\,x \ne 4.\)

Câu 2 (1 điểm)  Cho phương trình \({x^2} - \left( {m + 1} \right)x + m - 4 = 0\,\,\,\,\left( 1 \right),\,\,m\) là tham số.

a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1.\)

b) Tìm giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,\,{x_2}\) thỏa mãn: \(\left( {x_1^2 - m{x_1} + m} \right)\left( {x_2^2 - m{x_2} + m} \right) = 2.\)  

Câu 3 (1,5 điểm)  Đầu năm học, Hội khuyến học của một tỉnh tặng cho trường A tổng số \(245\) quyển sách gồm sách Toán và sách Ngữ văn. Nhà trường đã dùng \(\dfrac{1}{2}\) số sách Toán và \(\dfrac{2}{3}\) số sách Ngữ văn đó để phát cho các bạn học sinh có hoàn cảnh khó khăn. Biết rằng mỗi bạn nhận được một quyển sách Toán và một quyển sách Ngữ văn. Hỏi Hội khuyến học tỉnh đã tặng cho trường A mỗi loại sách bao nhiêu quyển?

Câu 4 (2 điểm)  Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AC\,\,\,\left( {BA < BC} \right).\) Trên đoạn thẳng \(OC\) lấy điểm \(I\) bất kì \(\left( {I \ne C} \right).\) Đường thẳng \(BI\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(D.\) Kẻ \(CH\) \(CH \bot BD\,\,\,\left( {H \in D} \right),\,\,DK \bot AC\,\,\left( {K \in AC} \right).\)

a) Chứng minh rằng tứ giác \(DHKC\) là tứ giác nội tiếp.

b) Cho độ dài đoạn thẳng \(AC\) là \(4cm\) và \(\angle ABD = {60^0}.\) Tính diện tích \(\Delta ACD.\)

c) Đường thẳng đi qua \(K\) song song với \(BC\) cắt đường thẳng \(BD\) tại \(E.\) Chứng minh rằng khi \(I\) thay đổi trên đoạn thẳng \(OC\,\,\left( {I \ne C} \right)\) thì điểm \(E\) luôn thuộc một đường tròn cố đinh.  

Câu 5 (0,5 điểm)  Cho \(x,\,\,y\) là các số thực thở mãn điều kiện \({x^2} + {y^2} = 1.\)

Tìm giá trị nhỏ nhất của biểu thức \(P = \left( {3 - x} \right)\left( {3 - y} \right).\)

Lời giải chi tiết

Phần trắc nghiệm:

Câu 1 - Căn thức bậc hai và hằng đẳng thức √A^(2)=|A|

Phương pháp:

Biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\)

Sử dụng công thức \(\sqrt {{f^2}\left( x \right)}  = \left| {f\left( x \right)} \right| = \left\{ \begin{array}{l}f\left( x \right)\,\,\,\,khi\,\,\,\,f\left( x \right) \ge 0\\ - f\left( x \right)\,\,\,\,khi\,\,\,f\left( x \right) < 0\end{array} \right..\)  

Cách giải:

Điều kiện: \({\left( {2 - x} \right)^2} \ge 0 \Leftrightarrow x - 2 \ne 0 \Leftrightarrow x \ne 2.\)

\(\begin{array}{l} \Rightarrow \sqrt {{{\left( {2 - x} \right)}^2}}  + x - 3 = \left| {2 - x} \right| + x - 3\\ = 2 - x + x - 3\,\,\,\,\,\left( {do\,\,\,\,\,x < 2 \Rightarrow 2 - x > 0} \right)\\ =  - 1.\end{array}\)

Chọn A.

Câu 2 - Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Phương pháp:

Đặt nhân tử chung ở tử số sau đó rút gọn phân thức hoặc sử dụng phương pháp trục căn thức ở mẫu.

Cách giải:

Ta có: \(\dfrac{{3 + \sqrt 3 }}{{\sqrt 3  + 1}} = \dfrac{{\sqrt 3 \left( {\sqrt 3  + 1} \right)}}{{\sqrt 3  + 1}} = \sqrt 3 .\)

Chọn B.

Câu 3 - Hàm số bậc nhất

Phương pháp:

Đường thẳng \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) có hệ số góc là \(a.\)

Cách giải:  

Đường thẳng \(y = 4x - 5\) có hệ số góc là \(a = 4.\) 

Chọn D.

Câu 4 - Đường thẳng song song và đường thẳng cắt nhau

Phương pháp:

Đường thẳng \(y = {a_1}x + {b_1}\) và \(y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)  

Cách giải:

Đường thẳng \(y = mx + 1\) song song với đường thẳng \(y = 2x - 3 \Leftrightarrow \left\{ \begin{array}{l}m = 2\\1 \ne  - 3\end{array} \right. \Leftrightarrow m = 2.\)

Chọn C.

Câu 5 - Căn bậc hai

Phương pháp:

Căn bậc hai số học của số dương \(a\) là \(\sqrt a .\)  

Cách giải:

Ta có căn bậc hai số học của \(144\) là \(\sqrt {144}  = 12.\)  

Chọn A.

Câu 6 - Đồ thị của hàm số y = ax + b (a ≠ 0)

Phương pháp:

Đường thẳng \(d:\,\,y = ax + b\) đi qua điểm \(M\left( {{x_0};\,\,{y_0}} \right) \Leftrightarrow {y_0} = a{x_0} + b.\)

Cách giải:

Đường thẳng \(y = \left( {2m + 1} \right)x + 3\) đi qua điểm \(A\left( { - 1;\,\,0} \right)\)

\( \Leftrightarrow 0 = \left( {2m + 1} \right).\left( { - 1} \right) + 3 \Leftrightarrow 2m + 1 = 3 \Leftrightarrow m = 1.\)

Chọn D.

Câu 7 - Căn bậc hai

Phương pháp:

Biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\)

Cách giải:

Biểu thức \(\sqrt {x - 3} \)  xác định \( \Leftrightarrow x - 3 \ge 0 \Leftrightarrow x \ge 3.\)

Chọn D.

Câu 8 - Phương trình bậc hai một ẩn số

Phương pháp:

Cách 1: Giải phương trình bằng cách đưa về phương trình tích.

Cách 2: Nhẩm nghiệm của phương trình: \(a{x^2} + bx + c = 0\,\,\,\left( * \right)\) có:

TH1: Nếu \(a + b + c = 0\) thì \(\left( * \right)\) có nghiệm \(x = 1\) và \(x = \dfrac{c}{a}.\)

TH2: Nếu \(a - b + c = 0\) thì \(\left( * \right)\) có nghiệm \(x =  - 1\) và \(x =  - \dfrac{c}{a}.\)

Cách 3: Thay các nghiệm ở các đáp án vào phương trình và chọn đáp án đúng.

Cách giải:

\(\begin{array}{l}{x^2} + x - 2 = 0 \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 2\\x = 1\end{array} \right..\end{array}\)

Chọn C.

Câu 9 - Một số hệ thức về cạnh và đường cao trong tam giác vuông

Phương pháp:

Sử dụng định lý Pitago đảo để làm bài toán.

Tam giác \(ABC\) có độ dài các cạnh lần lượt là \(a,\,\,b,\,\,c\) có \({a^2} = {b^2} + {c^2}\) thì \(\Delta ABC\) vuông.

Cách giải:

Ta có: \(\left\{ \begin{array}{l}A{B^2} = {3^2} = 9\\A{C^2} = {4^2} = 16\\B{C^2} = {5^2} = 25\end{array} \right. \Rightarrow B{C^2} = A{B^2} + A{C^2} = 25\)

\( \Rightarrow \Delta ABC\) là tam giác vuông tại \(A.\) (định lý Pitago đảo)

Chọn A.

Câu 10 - Phương trình bậc hai một ẩn số

Phương pháp:

Thay nghiệm \(x = 1\) vào phương trình đã cho để chọn đáp án đúng.

Cách giải:

Phương trình \({x^2} + bx + c = 0\) có nghiệm \(x = 1 \Rightarrow {1^2} + b.1 + c = 0 \Leftrightarrow b + c =  - 1.\)

Chọn B.

Câu 11 - Giải hệ phương trình bằng phương pháp cộng đại số

Phương pháp:

Giải hệ phương trình đã cho bằng phương pháp cộng đại số để tìm nghiệm \(\left( {{x_0};\,\,{y_0}} \right)\) sau đó tính tổng \({x_0} + {y_0}.\)

Cách giải:

Ta có: \(\left\{ \begin{array}{l}x - y = 1\\x + 2y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3y = 6\\x = y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 3\end{array} \right. \Rightarrow {x_0} + {y_0} = 3 + 2 = 5.\)

Chọn C.

Câu 12 - Hệ thức Vi-ét và ứng dụng

Phương pháp:

Phương trình \(a{x^2} + bx + c = 0\,\,\,\,\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) thì theo hệ thức Vi-et ta có: \({x_1} + {x_2} =  - \dfrac{b}{a}.\)

Cách giải:

Phương trình \({x^2} - 4x + 3 = 0\) có hai nghiệm \({x_1},\,\,{x_2} \Rightarrow {x_1} + {x_2} = 4.\)

Chọn D.

Câu 13 - Tỉ số lượng giác của góc nhọn

Phương pháp:

Xét tam giác \(ABC\) vuông tại \(A\) ta có: \(\sin \angle ABC = \dfrac{{AC}}{{BC}}.\)

Cách giải:  

Xét tam giác \(ABC\) vuông tại \(A\) ta có: \(\sin \angle ABC = \dfrac{{AC}}{{BC}} = \dfrac{2}{4} = \dfrac{1}{2}.\)

Chọn B.

Câu 14 - Ôn tập chương 3: Hệ hai phương trình bậc nhất một ẩn

Phương pháp:

Từ hệ phương trình bài cho và điều kiện \({x_0} = 2{y_0} \Rightarrow \) hai nghiệm của hệ phương trình ban đầu là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y = 3\\x = 2y\end{array} \right.\) từ đó ta tìm được \({x_0};\,\,{y_0}\) và thế vào phương trình \(mx - y = 3\) để tìm \(m.\)

Cách giải:

Theo đề bài ta có nghiệm \({x_0};\,\,{y_0}\) của hệ phương trình đã cho là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x + y = 3\\x = 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3y = 3\\x = 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 2\end{array} \right.\)

Lại có: \(mx - y = 3 \Rightarrow m.2 - 1 = 3 \Leftrightarrow 2m = 4 \Leftrightarrow m = 2.\)

Chọn B.

Câu 15 - Ôn tập tổng hợp chương 2, 3, 4 - Đại số

Phương pháp:

Giải phương trình hoành độ giao điểm \(\left( * \right)\) của hai đồ thị hàm số để tìm hoành độ giao điểm của hai đồ thị.

Thế hoành độ giao điểm vào công thức hàm số của một trong hai đồ thị hàm số đã cho để tìm tung độ giao điểm của hai đồ thị hàm số.

Cách giải:

Ta có phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:

\(\begin{array}{l}{x^2} = 2x + 3 \Leftrightarrow {x^2} - 2x - 3 = 0\\ \Leftrightarrow {x^2} - 3x + x - 3 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x =  - 1\end{array} \right.\\ + )\,\,\,x = 3 \Rightarrow y = {3^2} = 9 \Rightarrow A\left( {3;\,\,9} \right).\\ + )\,\,\,x =  - 1 \Rightarrow y = {\left( { - 1} \right)^2} \Rightarrow B\left( { - 1;\,\,1} \right).\end{array}\)

Vậy hai đồ thị hàm số cắt nhau tại hai điểm phân biệt \(A\left( {3;\,\,9} \right)\) và \(B\left( { - 1;\,\,1} \right).\)

Chọn A.

Câu 16 - Độ dài đường tròn, cung tròn

Phương pháp:

Số đo góc ở tâm bằng số đo cung bị chắn.

Trên đường tròn bán kính \(R,\) độ dài \(l\) của cung cung tròn có số đo cung \({n^0}\) được tính theo công thức: \(l = \dfrac{{\pi Rn}}{{180}}.\)

Cách giải:

Ta có: \(\angle AOB\) là góc ở tâm chắn cung nhỏ \(AB\)

Chọn D.

Câu 17 - Ôn tập tổng hợp chương 1, 2, 3 – Hình học

Phương pháp:

Áp dụng tính chất hai tiếp tuyến cắt nhau và góc nội tiếp chắn nửa đường tròn là góc vuông.

Cách giải:

Gọi \(O\) là trung điểm của \(AB.\)

Ta có: \(AC \bot AB = \left\{ A \right\} \Rightarrow AC\) cũng là tiếp tuyến của đường tròn \(\left( {O;\,\,\dfrac{{AB}}{2}} \right).\)  

\( \Rightarrow AC,\,\,\,MI\) là hai tiếp tuyến của \(\left( O \right)\) cắt nhau tại \(I.\)

\( \Rightarrow IM = IA\) (tính chất hai tiếp tuyến cắt nhau).

Ta có: \(\angle AMB\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right) \Rightarrow \angle AMB = {90^0}\) hay \(AM \bot BC = \left\{ M \right\} \Rightarrow \Delta AMC\) vuông tại \(M.\)

Ta có: \(\left\{ \begin{array}{l}\angle MAC + \angle MCA = {90^0}\,\,\,\left( {\angle AMC = {{90}^0}} \right)\\\angle AMI + \angle IMC = {90^0}\\\angle AMI = \angle MAI\end{array} \right.\) \( \Rightarrow \angle IMC = \angle MCI\)

\( \Rightarrow \Delta MIC\) là tam giác cân tại \(I \Rightarrow MI = IC.\)

\( \Rightarrow MI = IC = AI = \dfrac{{AC}}{2} = 10cm.\)

Chọn A.

Câu 18 - Ôn tập chương 2: Đường tròn

Phương pháp:

Đường kính đi qua trung điểm của dây cung thì vuông góc với dây ấy.

Cách giải:

Gọi \(H\) là trung điểm của \(AC.\)

Ta có \(\Delta ABC\) cân tại \(B \Rightarrow BH \bot AC \Rightarrow OB \bot AC = \left\{ H \right\}.\)

\( \Rightarrow BO\) là đường phân giác của \(\angle ABC \Rightarrow \angle ABO = {60^0}\)

Lại có \(\Delta ABO\) cân tại \(O\,\,\,\left( {OB = OA = R} \right)\)

\( \Rightarrow \Delta ABO\) là tam giác đều (tính chất).

\( \Rightarrow AB = AO = BO = 12cm.\)

Chọn B.

Câu 19 - Hệ thức Vi-ét và ứng dụng

Phương pháp:

Phương trình \(a{x^2} + bx + c = 0\,\,\,\,\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},\,\,{x_2} \Leftrightarrow \Delta  \ge 0.\)

Khi đó theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right..\)

Áp dụng biểu thức bài cho và hệ thức Vi-et để tìm \(m.\)

Đối chiếu với điều kiện rồi kết luận \(m.\)

\(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}.\)

Cách giải:

Phương trình \({x^2} + x + m + 1 = 0\,\,\,\left( * \right)\) có hai nghiệm \({x_1},\,\,{x_2} \Leftrightarrow \Delta  \ge 0\)

\( \Leftrightarrow 1 - 4\left( {m + 1} \right) \ge 0 \Leftrightarrow 1 - 4m - 4 \ge 0 \Leftrightarrow m \le  - \dfrac{3}{4}.\)

Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 1\\{x_2}{x_2} = m + 1\end{array} \right..\)  

Theo đề bài ta có: \(x_1^2 + x_2^2 = 5\)

\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 5\\ \Leftrightarrow {\left( { - 1} \right)^2} - 2\left( {m + 1} \right) = 5\\ \Leftrightarrow 1 - 2m - 2 = 5\\ \Leftrightarrow m =  - 3\,\,\,\,\left( {tm} \right).\end{array}\)

Chọn C.

Câu 20 - Hàm số bậc nhất

Phương pháp:

Hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) đồng biến khi \(a > 0\) và nghịch biến khi \(a < 0.\)

Hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) đồng biến \( \Rightarrow \forall {x_1} > {x_2}\) ta có: \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right).\)

Hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) nghịch biến \( \Rightarrow \forall {x_1} > {x_2}\) ta có: \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right).\)

Cách giải:

Hàm số \(y = f\left( x \right) = \left( {1 + {m^4}} \right)x + 1\) có \(a = 1 + {m^4} > 0\,\,\forall m \Rightarrow \) hàm số đã cho đồng biến trên \(\mathbb{R}.\)

Khi đó chỉ có đáp án C đúng vì \(2 < 3 \Rightarrow f\left( 2 \right) < f\left( 3 \right).\)

Chọn C.

Phần tự luận:

Câu 1 - Giải hệ phương trình bằng phương pháp cộng đại số

- Rút gọn biểu thức chứa căn thức bậc hai

Phương pháp:

a) Giải hệ phương trình bằng phương pháp cộng đại số.

b) Quy đồng mẫu các phân thức sau đó rút gọn biểu thức.

Cách giải:

a) Ta có: \(\left\{ \begin{array}{l}x - y = 2\\3x + 2y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 2y = 4\\3x + 2y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 15\\x - y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right.\).

Vậy hệ có nghiệm \(\left( {x;y} \right) = \left( {3;1} \right)\).

b) \(A = \left[ {\dfrac{{2\left( {x - 2\sqrt x  + 1} \right)}}{{x - 4}} - \dfrac{{2\sqrt x  - 1}}{{\sqrt x  + 2}}} \right]:\dfrac{{\sqrt x }}{{\sqrt x  - 2}}\) với \(x > 0;x \ne 4\)

\(\begin{array}{l}A = \left[ {\dfrac{{2\left( {x - 2\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} - \dfrac{{\left( {2\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}} \right]:\dfrac{{\sqrt x }}{{\sqrt x  - 2}}\\\,\,\,\,\, = \dfrac{{2x - 4\sqrt x  + 2 - 2x + \sqrt x  + 4\sqrt x  - 2}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}.\dfrac{{\sqrt x  - 2}}{{\sqrt x }}\\\,\,\,\,\, = \dfrac{{\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}.\dfrac{{\sqrt x  - 2}}{{\sqrt x }} = \dfrac{1}{{\sqrt x  + 2}}\end{array}\)

Vậy \(A = \dfrac{1}{{\sqrt x  + 2}}\).

Câu 2 - Ôn tập chương 4: Hàm số y = ax^2 (a ≠ 0) - Phương trình bậc hai một ẩn

Phương pháp:

a) Thay \(m = 1\) vào phương trình đã cho và giải phương trình bằng cách đưa phương trình về dạng phương trình tích.

b) Tìm điều kiện của \(m\) để phương trình đã cho có hai nghiệm \({x_1},\,\,{x_2}.\)

Áp dụng định lý Vi-et và hệ thức bài cho để tìm \(m.\)

Cách giải:

a) Khi \(m = 1\) thì \(\left( 1 \right)\) trở thành \({x^2} - \left( {1 + 1} \right)x + 1 - 4 = 0 \Leftrightarrow {x^2} - 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 3\end{array} \right.\).

Vậy với \(m = 1\) thì phương trình có tập nghiệm \(S = \left\{ { - 1;3} \right\}\).

b) Phương trình có hai nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}a = 1 \ne 0\\\Delta  = {\left( {m + 1} \right)^2} - 4\left( {m - 4} \right) \ge 0\end{array} \right.\)

\( \Leftrightarrow {m^2} + 2m + 1 - 4m + 16 \ge 0 \Leftrightarrow {m^2} - 2m + 17 \ge 0\) (luôn đúng do \({m^2} - 2m + 17 = {\left( {m - 1} \right)^2} + 16 > 0,\forall m\))

Do đó phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt \({x_1},{x_2}\).

Ta có: \({x^2} - \left( {m + 1} \right)x + m - 4 = 0 \Leftrightarrow {x^2} - mx - x + m - 4 = 0 \Leftrightarrow {x^2} - mx + m = x + 4\)

Do \({x_1},{x_2}\) là nghiệm của \(\left( 1 \right)\) nên \(\left\{ \begin{array}{l}x_1^2 - m{x_1} + m = {x_1} + 4\\x_2^2 - m{x_2} + m = {x_2} + 4\end{array} \right.\)

Thay vào đẳng thức bài cho ta được \(\left( {{x_1} + 4} \right)\left( {{x_2} + 4} \right) = 2\)

\( \Leftrightarrow {x_1}{x_2} + 4\left( {{x_1} + {x_2}} \right) + 16 = 2 \Leftrightarrow {x_1}{x_2} + 4\left( {{x_1} + {x_2}} \right) + 14 = 0\,\,\left( 2 \right)\)

Theo định lý Vi – et \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 1\\{x_1}{x_2} = m - 4\end{array} \right.\), thay vào \(\left( 2 \right)\) ta được:

\(m - 4 + 4\left( {m + 1} \right) + 14 = 0 \Leftrightarrow 5m + 14 = 0 \Leftrightarrow m =  - \dfrac{{14}}{5}\).

Vậy \(m =  - \dfrac{{14}}{5}\) là giá trị cần tìm.

Câu 3 - Giải bài toán bằng cách lập phương trình

Phương pháp:

Gọi số sách Toán Hội khuyến học tỉnh tặng cho trường A là \(x\) quyển \(\left( {0 < x < 245;\,x \in \mathbb{N}} \right)\)

Biểu diễn các đại lượng chưa biết theo \(x\) và các đại lượng đã biết.

Từ đó lập phương trình và giải phương trình tìm \(x.\)

Đối chiếu với điều kiện rồi kết luận.

Cách giải:

Gọi số sách Toán Hội khuyến học tỉnh tặng cho trường A là \(x\) quyển \(\left( {0 < x < 245;\,x \in \mathbb{N}} \right)\)

Thì số sách Ngữ văn Hội khuyến học tỉnh tặng cho trường A là \(245 - x\) quyển

Số sách Toán nhà trường dùng để phát cho học sinh khó khăn là \(\dfrac{1}{2}x\) quyển

Số sách Ngữ văn nhà trường dùng để phát cho học sinh khó khăn là \(\dfrac{2}{3}\left( {245 - x} \right)\) quyển

Vì mỗi bạn nhận được 1 quyển sách Toán và 1 quyển sách Ngữ văn nên số quyển sách Toán và quyển sách Ngữ Văn đem phát là bằng nhau.

Ta có phương trình \(\dfrac{1}{2}x = \dfrac{2}{3}\left( {245 - x} \right)\)

\(\begin{array}{l} \Leftrightarrow \dfrac{1}{2}x = \dfrac{{490}}{3} - \dfrac{{2x}}{3} \Leftrightarrow \dfrac{7}{6}x = \dfrac{{490}}{3}\\ \Leftrightarrow x = \dfrac{{490}}{3}:\dfrac{7}{6} \Leftrightarrow x = 140\,\left( {tm} \right)\end{array}\)

Vậy số sách Toán Hội khuyến học tỉnh tặng cho trường A là \(140\) quyển.

Số sách Ngữ văn Hội khuyến học tỉnh tặng cho trường A là \(245 - 140 = 105\) quyển.

Câu 4 - Bài tập ôn cuối năm

Phương pháp:

a) Sử dụng các dấu hiệu nhận biết để chứng minh tứ giác nội tiếp.

b) Sử dụng các tính chất góc nội tiếp của đường tròn và công thức tính diện tích tam giác.

Cách giải:

a) Xét tứ giác \(DHKC\) có

\(\angle DHC = 90^\circ \,\)(do \(CH \bot BD\))

\(\angle DKC = 90^\circ \) (do \(DK \bot AC\))

Suy ra \(\angle DHC = \angle DKC\left( { = 90^\circ } \right)\) nên hai đỉnh \(H;K\)  kề nhau cùng nhìn cạnh \(CD\) dưới các góc vuông nên tứ giác \(DHKC\) là tứ giác nội tiếp.

b) Gọi \(O\) là trung điểm \(AC\)

Xét đường tròn \(\left( O \right)\) có  \(\angle ABD = 60^\circ  \Rightarrow \angle ACD = \angle ABD = 60^\circ \) (hai góc nội tiếp cùng chắn cung \(AD\))

Lại có \(\angle CDA = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Xét tam giác \(ACD\) vuông tại \(D\) có \(AC = 4cm;\,\angle ACD = 60^\circ \) nên \(AD = AC.\sin \angle ACD = 4.\sin 60^\circ  = 2\sqrt 3 \,cm\)

Và \(CD = AC.\cos \angle ACD = 4.\cos 60^\circ  = 2\,cm\)

Diện tích tam giác \(ACD\) là \({S_{\Delta ACD}} = \dfrac{1}{2}AD.DC = \dfrac{1}{2}.2\sqrt 3 .2 = 2\sqrt 3 \,c{m^2}.\)

c) Vì \(EK//BC \Rightarrow \angle DEK = \angle DBC\) (1) (hai góc ở vị trí đồng vị)

Xét đường tròn \(\left( O \right)\) có \(\angle DBC = \angle DAC\) (2) (hai góc nội tiếp cùng chắn cung \(CD\))

Từ (1) và (2) suy ra \(\angle DEK = \angle DAK\)

Suy ra tứ giác \(AEKD\) có hai đỉnh \(A,E\)  cùng nhìn cạnh \(KD\) dưới các góc bằng nhau nên tứ giác \(AEKD\) là tứ giác nội tiếp, suy ra \(\angle AED = \angle AKD = 90^\circ \)

Do đó \(AE \bot EB\) suy ra \(\Delta AEB\) vuông tại \(E.\)

Lại có \(AB\) cố định nên \(E\) thuộc đường tròn đường kính \(AB\) cố định khi \(I\) thay đổi trên đoạn \(OC.\)

Câu 5 (VDC) - Tìm giá trị lớn nhất, giá trị nhỏ nhất

Phương pháp:

Sử dụng bất đẳng thức Bu-nhi-a Cop-xki.

Cách giải:

Áp dụng bất đẳng thức Bu-nhi-a Cop-xki ta có:

\({\left( {x + y} \right)^2} \le \left( {{1^2} + {1^2}} \right)\left( {{x^2} + {y^2}} \right) = 2 \Rightarrow x + y \le \sqrt 2 \)

Lại có: \(P = \left( {3 - x} \right)\left( {3 - y} \right) = 9 - 3\left( {x + y} \right) + xy = 9 - 3\left( {x + y} \right) + \dfrac{{{{\left( {x + y} \right)}^2} - \left( {{x^2} + {y^2}} \right)}}{2}\)

\( = 9 - 3\left( {x + y} \right) + \dfrac{{{{\left( {x + y} \right)}^2} - 1}}{2} = \dfrac{{{{\left( {x + y} \right)}^2} - 6\left( {x + y} \right) + 17}}{2}\) \( = \dfrac{{\left[ {{{\left( {x + y} \right)}^2} - 6\left( {x + y} \right) + 9} \right] + 8}}{2} = \dfrac{1}{2}{\left( {x + y - 3} \right)^2} + 4\)

Vì \(x + y \le \sqrt 2 \) nên \(x + y - 3 \le \sqrt 2  - 3 < 0 \Rightarrow {\left( {x + y - 3} \right)^2} \ge {\left( {\sqrt 2  - 3} \right)^2} = 11 - 6\sqrt 2 \)

\( \Rightarrow P = \dfrac{1}{2}{\left( {x + y - 3} \right)^2} + 4 \ge \dfrac{{11 - 6\sqrt 2 }}{2} + 4 = \dfrac{{19}}{2} - 3\sqrt 2 \)

\( \Rightarrow P \ge \dfrac{{19}}{2} - 3\sqrt 2 \).

Dấu “=” xảy ra khi \(x = y = \dfrac{{\sqrt 2 }}{2}\).