Đề thi vào 10 môn Toán Bắc Giang năm 2018Tải vềCâu I (2,0 điểm) Tính giá trị của biểu thức Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài Câu I (2,0 điểm)
Câu II (3,0 điểm)
a) Rút gọn biểu thức B. b) Đặt \(C = B.\left( {a - \sqrt a + 1} \right)\). So sánh C và 1.
a) Giải phương trình (1) khi \(m = - 1.\) b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};\,\,{x_2}\) sao cho \({x_1};\,\,{x_2}\) là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5. Câu III (1,5 điểm) Bạn Linh đi xe đạp từ nhà đến trường với quãng đường 10 km. Khi đi từ trường về nhà, vẫn trên cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Linh phải giảm vận tốc 2 km/h so với khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là 15 phút. Tính vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường. Câu IV (3,0 điểm) Cho tam giác \(ABC\) nhọn. Đường tròn tâm O đường kính BC cắt các cạnh \(AB,AC\) lần lượt tại các điểm \(M,N\,\,\left( {M \ne B,N \ne C} \right)\). Gọi H là giao điểm của BN và CM; P là giao điểm của AH và BC.
Câu V (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{81{x^2} + 18225x + 1}}{{9x}} - \dfrac{{6\sqrt x + 8}}{{x + 1}}\) với \(x > 0\) Lời giải chi tiết Câu I. Phương pháp:
Cách giải:
\(\begin{array}{l}A = \sqrt 5 \left( {\sqrt {20} - \sqrt 5 } \right) + 1\\A = \sqrt 5 \left( {\sqrt {{2^2}.5} - \sqrt 5 } \right) + 1\\A = \sqrt 5 \left( {2\sqrt 5 - \sqrt 5 } \right) + 1\\A = \sqrt 5 .\sqrt 5 + 1\\A = 5 + 1\\A = 6\end{array}\)
Đường thẳng \(y = \left( {m - 1} \right)x + 2018\) có hệ số góc bằng 3 \( \Leftrightarrow m - 1 = 3 \Leftrightarrow m = 4\). Câu II. Phương pháp:
b) Quy đồng, rút gọn biểu thức B. Tính C và sử dụng BĐT Cauchy để so sánh C với 1. Cách giải: 1. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 4y = 8\\2x + 5y = 13\end{array} \right.\) \(\left\{ \begin{array}{l}x + 4y = 8\\2x + 5y = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 8y = 16\\2x + 5y = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3y = 3\\x = 8 - 4y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 4\end{array} \right.\). Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {4;1} \right)\). 2. Cho biểu thức \(B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{a\sqrt a - a - \sqrt a + 1}}} \right).\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\) (với \(a > 0,\,a \ne 1\)) a) Rút gọn biểu thức B. Với \(a > 0,\,a \ne 1\) ta có: \(\begin{array}{l}B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{a\sqrt a - a - \sqrt a + 1}}} \right).\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{a\left( {\sqrt a - 1} \right) - \left( {\sqrt a - 1} \right)}}} \right).\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{\left( {\sqrt a - 1} \right)\left( {a - 1} \right)}}} \right).\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{{6\left( {\sqrt a - 1} \right) + 10 - 2\sqrt a }}{{\left( {\sqrt a - 1} \right)\left( {a - 1} \right)}}.\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{{6\sqrt a - 6 + 10 - 2\sqrt a }}{{\left( {\sqrt a - 1} \right)\left( {a - 1} \right)}}.\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{{4\left( {\sqrt a + 1} \right)}}{{{{\left( {\sqrt a - 1} \right)}^2}\left( {\sqrt a + 1} \right)}}.\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{4}{{{{\left( {\sqrt a - 1} \right)}^2}}}.\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{1}{{\sqrt a }}\end{array}\) b) Đặt \(C = B.\left( {a - \sqrt a + 1} \right)\). So sánh C và 1. \(\begin{array}{l}B = \dfrac{1}{{\sqrt a }} \Rightarrow C = B.\left( {a - \sqrt a + 1} \right)\\ \Rightarrow C = \dfrac{1}{{\sqrt a }}\left( {a - \sqrt a + 1} \right) = \sqrt a - 1 + \dfrac{1}{{\sqrt a }}\end{array}\) Áp dụng BĐT Cauchy ta có \(\sqrt a + \dfrac{1}{{\sqrt a }} \ge 2\sqrt {\sqrt a .\dfrac{1}{{\sqrt a }}} = 2 \Rightarrow \sqrt a - 1 + \dfrac{1}{{\sqrt a }} \ge 2 - 1 = 1\) Dấu bằng xảy ra \( \Leftrightarrow \sqrt a = \dfrac{1}{{\sqrt a }} \Leftrightarrow a = 1\). Vậy \(C \ge 1\) và \(C = 1 \Leftrightarrow a = 1\). 3. Cho phương trình \({x^2} - \left( {m + 2} \right)x + 3m - 3 = 0\,\,\left( 1 \right)\), với x là ẩn, m là tham số. a) Giải phương trình (1) khi \(m = - 1.\) Thay \(m = - 1\) vào phương trình (1) ta có: \(\begin{array}{l}\,\,\,\,\,\,{x^2} - x - 6 = 0\\ \Leftrightarrow {x^2} - 3x + 2x - 6 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + 2\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 2\end{array} \right.\end{array}\) Vậy khi \(m = - 1\) thì tập nghiệm của phương trình là \(S = \left\{ { - 2;3} \right\}\). b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};\,\,{x_2}\) sao cho \({x_1};\,\,{x_2}\) là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5. Hai nghiệm \({x_1};{x_2}\) là hai cạnh của một tam giác vuông nên \({x_1};{x_2} > 0\) Để phương trình có hai nghiệm phân biệt dương \({x_1};\,\,{x_2}\) \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S = {x_1} + {x_2} > 0\\P = {x_1}.{x_2} > 0\end{array} \right.\left( * \right)\) Khi đó theo hệ thức Vi-ét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}{x_2} = 3m - 3\end{array} \right.\) \(\left( * \right) \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 2} \right)^2} - 4\left( {3m - 3} \right) > 0\\m + 2 > 0\\3m - 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 4} \right)^2} > 0\\m + 2 > 0\\3m - 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\m > - 2\\m > 1\end{array} \right. \Leftrightarrow m > 1;m \ne 4\) Vì \({x_1};\,\,{x_2}\) là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5 nên áp dụng định lí Pi-ta-go ta có: \(\begin{array}{l}\,\,\,\,\,\,x_1^2 + x_2^2 = {5^2} = 25\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 25\\ \Leftrightarrow {\left( {m + 2} \right)^2} - 2\left( {3m - 3} \right) = 25\\ \Leftrightarrow {m^2} + 4m + 4 - 6m + 6 = 25\\ \Leftrightarrow {m^2} - 2m - 15 = 0\\ \Leftrightarrow {m^2} - 5m + 3m - 15 = 0\\ \Leftrightarrow m\left( {m - 5} \right) + 3\left( {m - 5} \right) = 0\\ \Leftrightarrow \left( {m - 5} \right)\left( {m + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 5\left( {tm} \right)\\m = - 3\left( {ktm} \right)\end{array} \right.\,\,\end{array}\) Vậy \(m = 5\) thỏa mãn điều kiện bài toán. Câu III. Phương pháp: - Gọi vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường là \(x\,\,\left( {km/h} \right)\) (ĐK: \(x > 2\)) - Tính vận tốc của xe đạp khi bạn Linh đi từ trường về nhà. - Tính thời gian đi từ nhà đến trường và thời gian đi từ trường về nhà. - Do thời gian về nhà nhiều hơn thời gian đến trường là 15 phút \( = \dfrac{{15}}{{60}} = \dfrac{1}{4}\,\left( h \right)\) nên ta có phương trình: Thời gian đi từ trường về nhà – thời gian đi từ nhà đến trường \( = \dfrac{1}{4}\). Cách giải: Bạn Linh đi xe đạp từ nhà đến trường với quãng đường 10 km. Khi đi từ trường về nhà, vẫn trên cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Linh phải giảm vận tốc 2 km/h so với khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là 15 phút. Tính vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường. Gọi vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường là \(x\,\,\left( {km/h} \right)\) (ĐK: \(x > 2\)) Khi đó vận tốc của xe đạp khi bạn Linh đi từ trường về nhà là \(x - 2\,\,\left( {km/h} \right)\). Thời gian bạn Linh đi từ nhà đến trường là \(\dfrac{{10}}{x}\,\,\left( h \right)\) Thời gian bạn Linh đi từ trường về nhà là \(\dfrac{{10}}{{x - 2}}\,\,\left( h \right)\) Do thời gian về nhà nhiều hơn thời gian đến trường là 15 phút \( = \dfrac{{15}}{{60}} = \dfrac{1}{4}\,\left( h \right)\) nên ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\dfrac{{10}}{{x - 2}} - \dfrac{{10}}{x} = \dfrac{1}{4}\\ \Leftrightarrow 40x - 40\left( {x - 2} \right) = x\left( {x - 2} \right)\\ \Leftrightarrow 40x - 40x + 80 = {x^2} - 2x\\ \Leftrightarrow {x^2} - 2x - 80 = 0\\ \Leftrightarrow {x^2} - 10x + 8x - 80 = 0\\ \Leftrightarrow x\left( {x - 10} \right) + 8\left( {x - 10} \right) = 0\\ \Leftrightarrow \left( {x - 10} \right)\left( {x + 8} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 10\,\,\,\left( {tm} \right)\\x = - 8\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường là 10 km/h. Câu IV. Phương pháp:
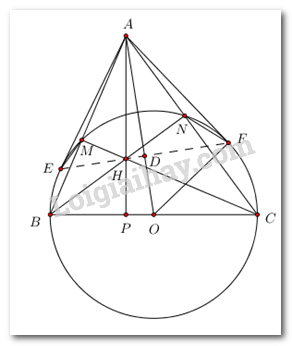
Tam giác ABC đều \( \Rightarrow \) Trực tâm H là trọng tâm của tam giác ABC \( \Rightarrow AH = \dfrac{2}{3}AP\). Tính AH, suy ra bán kính và tính chu vi đường tròn ngoại tiếp tam giác tứ giác AMHN. 4. Gọi \(D = AO \cap EF\), chứng minh \(HD \bot AO\) và \(EF \bot AO \Rightarrow EF \equiv HD\). Cách giải: Cho tam giác \(ABC\) nhọn. Đường tròn tâm O đường kính BC cắt các cạnh \(AB,AC\) lần lượt tại các điểm \(M,N\,\,\left( {M \ne B,N \ne C} \right)\). Gọi H là giao điểm của BN và CM; P là giao điểm của AH và BC.
1. Chứng minh tứ giác AMHN nội tiếp được trong một đường tròn. Ta có \(\widehat {BMC} = \widehat {BNC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {AMH} = \widehat {ANH} = {90^0}\) \( \Rightarrow \) Tứ giác \(AMHN\) có \(\widehat {AMH} + \widehat {ANH} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác AMHN là tứ giác nội tiếp đường tròn đường kính AH (Tứ giác có tổng hai góc đối bằng 1800). 2. Chứng minh \(BM.BA = BP.BC\). Xét \(\Delta ABP\) và \(\Delta CBM\) có: \(\widehat {APB} = \widehat {CMB} = {90^0}\) ; \(\widehat {ABC}\) chung; \( \Rightarrow \Delta ABP \sim \Delta CBM\,\,\left( {g.g} \right) \Rightarrow \dfrac{{BA}}{{BP}} = \dfrac{{BC}}{{BM}} \Rightarrow BM.BA = BP.BC\) 3. Trong trường hợp đặc biệt khi tam giác \(ABC\) đều cạnh bằng \(2a\) . Tính chu vi đường tròn ngoại tiếp tứ giác AMHN. Ta có \(BN \bot AC;\,\,CM \bot AB;\,\,BN \cap CM = H \Rightarrow H\) là trực tâm tam giác ABC. \(\Delta ABC\) đều \( \Rightarrow \widehat {ABP} = \widehat {ABC} = {60^0}\) Xét tam giác vuông ABP có \(AP = AB.\sin {60^0} = 2a.\dfrac{{\sqrt 3 }}{2} = a\sqrt 3 \) Do H là trực tâm tam giác ABC nên đồng thời H cũng là trọng tâm của tam giác ABC\( \Rightarrow AH = \dfrac{2}{3}AP = \dfrac{2}{3}a\sqrt 3 = \dfrac{{2a\sqrt 3 }}{3}\) Vì AH là đường kính của đường tròn ngoại tiếp tứ giác AMHN nên bán kính của đường tròn ngoại tiếp tứ giác AMHN là \(\dfrac{{AH}}{2} = \dfrac{{a\sqrt 3 }}{3}\). Vậy chu vi đường tròn ngoại tiếp tứ giác AMHN là \(C = 2\pi .\dfrac{{a\sqrt 3 }}{3} = \dfrac{{2\pi a\sqrt 3 }}{3}\). 4. Từ điểm A kẻ các tiếp tuyến AE và AF của đường tròn tâm O đường kính BC (E, F là các tiếp điểm). Chứng minh ba điểm \(E,H,F\) thẳng hàng. Gọi D là giao điểm của OA và EF. H là trực tâm tam giác ABC \( \Rightarrow AH \bot BC \Rightarrow AP \bot BC \Rightarrow \widehat {APC} = {90^0}\) \(\widehat {BNC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {ANH} = {90^0}\) Xét \(\Delta AHN\) và \(\Delta ACP\) có : \(\widehat {ANH} = \widehat {APC} = {90^0}\) (cmt) \(\widehat {PAC}\) chung ; \( \Rightarrow \Delta AHN \sim \Delta ACP\,\left( {g.g} \right) \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AN}}{{AP}} \Rightarrow AH.AP = AN.AC\,\,\,\left( 1 \right)\) Xét \(\Delta AFN\) và \(\Delta ACF\) có : \(\widehat {FAC}\) chung ; \(\widehat {AFN} = \widehat {ACF}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung NF). \( \Rightarrow \Delta AFN \sim \Delta ACF\,\,\left( {g.g} \right) \Rightarrow \dfrac{{AF}}{{AC}} = \dfrac{{AN}}{{AF}} \Rightarrow AN.AC = A{F^2}\,\,\,\left( 2 \right)\) Ta có \(AF \bot OF\,\,\left( {gt} \right) \Rightarrow \Delta OAF\) vuông tại F. Có \(AE = AF\,\) (tính chất hai tiếp tuyến cắt nhau) ; \(OE = OF\,\,\left( { = R} \right) \Rightarrow OA\) là trung trực của EF. \( \Rightarrow OA \bot EF \Rightarrow FD\) là đường cao của tam giác vuông OAF. \( \Rightarrow A{F^2} = AD.AO\,\,\,\left( 3 \right)\) (hệ thức lượng trong tam giác vuông). Từ (1), (2) và (3) \( \Rightarrow AH.AP = AD.AO \Rightarrow \dfrac{{AH}}{{AO}} = \dfrac{{AD}}{{AP}}\) Xét \(\Delta AHD\) và \(\Delta AOP\) có: \(\widehat {OAP}\) chung; \(\dfrac{{AH}}{{AO}} = \dfrac{{AD}}{{AP}}\,\,\left( {cmt} \right)\); \( \Rightarrow \Delta AHD \sim \Delta AOP\,\,\left( {c.g.c} \right)\). \( \Rightarrow \widehat {ADH} = \widehat {APO} = {90^0} \Rightarrow HD \bot OA\) Từ đó ta có qua điểm D ta kẻ được \(EF \bot OA\) (cmt) và \(HD \bot OA \Rightarrow EF \equiv HD\). Vậy ba điểm \(E,H,F\) thẳng hàng. Câu V. Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{81{x^2} + 18225x + 1}}{{9x}} - \dfrac{{6\sqrt x + 8}}{{x + 1}}\) với \(x > 0\) Ta có: \(\begin{array}{l}P = \dfrac{{81{x^2} + 18225x + 1}}{{9x}} - \dfrac{{6\sqrt x + 8}}{{x + 1}}\\P = 9x + 2025 + \dfrac{1}{{9x}} - \dfrac{{6\sqrt x + 8}}{{x + 1}}\end{array}\) Ta chứng minh \(\dfrac{{6\sqrt x + 8}}{{x + 1}} \le 9\,\,\forall x > 0\). Giả sử : \(\begin{array}{l}\,\,\,\,\,\,\dfrac{{6\sqrt x + 8}}{{x + 1}} \le 9\\ \Leftrightarrow \dfrac{{6\sqrt x + 8}}{{x + 1}} - \dfrac{{9x + 9}}{{x + 1}} \le 0\\ \Leftrightarrow \dfrac{{6\sqrt x + 8 - 9x - 9}}{{x + 1}} \le 0\\ \Leftrightarrow \dfrac{{ - 9x + 6\sqrt x - 1}}{{x + 1}} \le 0\\ \Leftrightarrow \dfrac{{ - {{\left( {3\sqrt x - 1} \right)}^2}}}{{x + 1}} \le 0\end{array}\) Ta có \(x > 0 \Leftrightarrow x + 1 > 1;\,\,{\left( {3\sqrt x - 1} \right)^2} \ge 0 \Rightarrow \dfrac{{ - {{\left( {3\sqrt x - 1} \right)}^2}}}{{x + 1}} \le 0\,\,\forall x > 0\) \( \Rightarrow \dfrac{{6\sqrt x + 8}}{{x + 1}} \le 9\,\,\forall x > 0 \Rightarrow - \dfrac{{6\sqrt x + 8}}{{x + 1}} \ge - 9\forall x > 0\) \(\begin{array}{l} \Rightarrow P \ge 2\sqrt {9x.\dfrac{1}{{9x}}} + 2025 - 9\\ \Leftrightarrow P \ge 2018\end{array}\) Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}9x = \dfrac{1}{{9x}}\\3\sqrt x - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}81{x^2} = 1\\\sqrt x = \dfrac{1}{3}\end{array} \right. \Leftrightarrow x = \dfrac{1}{9}\). Vậy \({P_{\min }} = 2018 \Leftrightarrow x = \dfrac{1}{9}\).
|




















Danh sách bình luận