Đề thi vào 10 môn Toán Bắc Giang năm 2021Tải vềPHẦN I. TRẮC NGHIỆM (3,0 điểm) Câu 1. Đồ thị hàm số Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
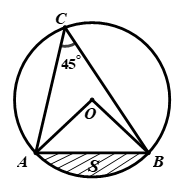
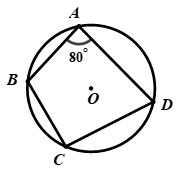
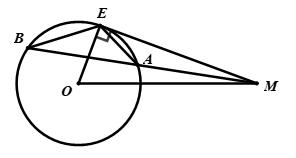
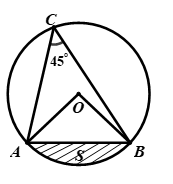
Đề bài PHẦN I. TRẮC NGHIỆM (3,0 điểm) Câu 1. Đồ thị hàm số \(y = 2{x^2}\) đi qua điểm nào trong các điểm cho dưới đây? A. \(P\left( { - 1; - 2} \right)\) B. \(Q\left( {0;2} \right)\) C. \(M\left( { - 1;2} \right)\) D. \(N\left( {1; - 2} \right)\) Câu 2. Với \(x \ge 0\) thỏa mãn \(\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right) = 1\), giá trị của biểu thức \({x^2} - 5x - 3\) bằng: A. \( - 3\) B. \(4\) C. \(8\) D. \( - 4\) Câu 3. Căn bậc hai số học của \(16\) là: A. \( - 8\) B. \(4\) C. \(8\) D. \( - 4\) Câu 4. Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\), biết góc \(\angle BAD = {80^0}\). Tính góc \(\angle BCD\). A. \(\angle BCD = {50^0}\) B. \(\angle BCD = {100^0}\) C. \(\angle BCD = {10^0}\) D. \(\angle BCD = {40^0}\) Câu 5. Gọi \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y = 1\\2x + y = m\end{array} \right.\) (\(m\) là tham số). Tìm \(m\) để biểu thức \(P = x_0^2 + y_0^2\) đạt giá trị nhỏ nhất. A. \(m = 3\) B. \(m = - 3\) C. \(m = - \dfrac{3}{2}\) D. \(m = \dfrac{3}{2}\) Câu 6. Tất cả các giá trị của \(x\) để biểu thức \(\sqrt {x - 2} \) có nghĩa là: A. \(x > 2\) B. \(x \ge 0\) C. \(x \le 2\) D. \(x \ge 2\) Câu 7. Giá trị của biểu thức \(\sqrt {25} + \sqrt 9 - \sqrt {36} \) bằng: A. \(3\) B. \(14\) C. \(2\) D. \(12\) Câu 8. Biết hệ phương trình \(\left\{ \begin{array}{l}ax + 2y = - 1\\bx - ay = 5\end{array} \right.\) (\(a,b\) là tham số) có một nghiệm là \(\left( {x;y} \right) = \left( {3; - 2} \right)\). Khi đó: A. \(a = - 1;b = 1\) B. \(a = 1;b = - 1\) C. \(a = - 1;b = 2\) D. \(a = 1;b = 1\) Câu 9. Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \left( {m - 2} \right)x + \dfrac{1}{{\sqrt {6 - m} }}\) (với \(m \ne 2\)) đồng biến trên \(\mathbb{R}?\) A. \(4\) B. \(3\) C. Vô số D. \(5\) Câu 10. Hệ số góc của đường thẳng \(y = \sqrt 5 x - 2\) là: A. \(\sqrt 5 \) B. \(1\) C. \( - 2\) D. \(\dfrac{1}{{\sqrt 5 }}\) Câu 11. Phương trình \({x^2} - 3x + 2 = 0\) có nghiệm là: A. \(S = \left\{ { - 1;2} \right\}\) B. \(S = \left\{ { - 2; - 1} \right\}\) C. \(S = \left\{ {1; - 2} \right\}\) D. \(S = \left\{ {1;2} \right\}\) Câu 12. Tất cả các giá trị của tham số \(m\) để phương trình \({x^2} - 2x + m = 0\) có nghiệm là: A. \(m \ge 1\) B. \(m > 1\) C. \(m \le 1\) D. \(m < 1\) Câu 13. Cho đường tròn \(\left( O \right)\), bán kính \(R = 5\). Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\), kẻ cát tuyến \(MAB\) với đường tròn \(\left( O \right)\). Tính \(MA.MB\), biết \(OM = 8\). A. \(89\) B. \(23\) C. \(39\) D. \(40\) Câu 14. Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\), bán kính \(R = 6cm\) và góc \(\angle ACB = {45^0}\). Phần gạch sọc (như hình vẽ bên dưới) có diện tích là \(S\). Khi đó A. \(S = \dfrac{9}{2}\left( {\pi - 2} \right)c{m^2}\) B. \(S = 9\left( {\pi + 1} \right)c{m^2}\) C. \(S = 3\left( {\pi + 2} \right)c{m^2}\) D. \(S = 9\left( {\pi - 2} \right)c{m^2}\) Câu 15. Cho tam giác \(ABC\) vuông tại \(A\), biết \(BC = 5cm\) và \(AC = 3cm\). Độ dài cạnh \(AB\) bằng: A. \(4cm\) B. \(2cm\) C. \(\sqrt {34} cm\) D. \(16cm\) II. TỰ LUẬN (7,0 điểm) Câu 1 (3,0 điểm): 1) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - y = 4\\2x + y = 5\end{array} \right.\) 2) Rút gọn biểu thức \(P = \left( {\dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{x + \sqrt x }}} \right):\dfrac{{\sqrt x - 1}}{{x + 2\sqrt x + 1}}\) với \(x > 0\) và \(x \ne 1\). 3) Cho phương trình \({x^2} - 2x + m - 3 = 0\,\,\left( 1 \right)\) (ẩn \(x\), tham số \(m\)) a) Giải phương trình \(\left( 1 \right)\) khi \(m = - 5\) b) Tìm \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 + 4{x_1}{x_2} + 3x_2^2 = 0\) Câu 2 (1,5 điểm): Để hỗ trợ bệnh nhân điều trị COVID – 19, nhà máy A xây dựng kế hoạch sản xuất một loại máy thở với số lượng 300 chiếc trong một thời gian đã định. Khi sản xuất thực tế, mỗi nhà máy A sản xuất được nhiều hơn 5 máy thở so với số máy phải sản xuất trong một ngày theo kế hoạch. Vì thế thời gian hoàn thành công việc sớm hơn 10 ngày so với kế hoạch. Hỏi theo kế hoạch, mỗi ngày nhà máy A sản xuất bao nhiêu chiếc máy thở, biết số máy sản xuất trong mỗi ngày là như nhau? Câu 3 (2,0 điểm) Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Gọi \(AH\) là đường cao của tam giác \(ABC\,\left( {H \in BC} \right)\). Kẻ \(HE\) vuông góc với \(AB\,\left( {E \in AB} \right),\,HF\) vuông góc với \(AC\,\left( {F \in AC} \right).\) 1) Chứng minh tứ giác \(AEHF\) nội tiếp trong một đường tròn. 2) Đường thẳng \(EF\) cắt đường tròn \(\left( O \right)\) tại hai điểm \(M,N\)\((M\) thuộc cung nhỏ \(AB)\). Chứng minh số đo cung \(ABC = \)số đo cung \({\rm{AF}}M\) và \(AH = AN.\) Câu 4 (0,5 điểm) Cho hai số thực \(a,b\) thay đổi thỏa mãn \(1 \le a \le 2,\,\,\,1 \le b \le 2.\) Chứng minh \(\left( {a + b} \right)\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right) \le \dfrac{9}{2}.\) Lời giải chi tiết PHẦN I. TRẮC NGHIỆM
Câu 1 Phương pháp: Đồ thị hàm số \(\left( P \right):y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) khi \(\left( P \right):{y_A} = a{x_A}^2\left( {a \ne 0} \right)\) Cách giải: + Thay \(x = - 1\) vào \(y = 2{x^2}\), ta được \(y = 2.{\left( { - 1} \right)^2} = 2\) Đồ thị hàm số \(y = 2{x^2}\) đi qua điểm \(\left( { - 1;2} \right)\). Chọn C. Câu 2 Phương pháp: Giải phương trình \(\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right) = 1\), tìm nghiệm thỏa mãn điều kiện Thay nghiệm vừa tìm được của phương trình vào biểu thức \({x^2} - 5x - 3\) để tính. Cách giải: Ta có: \(\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right) = 1\) \(\begin{array}{l} \Leftrightarrow x - 4 = 1\\ \Leftrightarrow x = 3\left( {tmdk} \right)\end{array}\) Với \(x = 3\), thay vào biểu thức \({x^2} - 5x - 3\), ta được: \({3^2} - 5.3 - 3 = - 3\) Chọn A. Câu 3 Phương pháp: Với số dương \(a\), số \(\sqrt a \) được gọi là căn bậc hai số học của \(a\). Cách giải: Căn bậc hai số học của \(16\) là \(\sqrt {16} = 4\) Chọn B. Câu 4 Phương pháp: Sử dụng tính chất của tứ giác nội tiếp Cách giải:
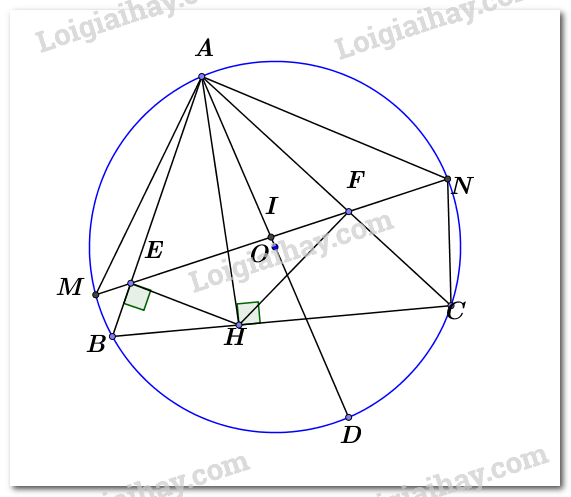
Tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) \( \Rightarrow \angle BAD + \angle BCD = {180^0}\) (tính chất của tứ giác nội tiếp) \( \Rightarrow \angle BCD = {180^0} - \angle BAD = {180^0} - {80^0} = {100^0}\) Chọn B. Câu 5 Phương pháp: Sử dụng phương pháp cộng đại số, tìm nghiệm \(\left( {{x_0};{y_0}} \right)\) của hệ phương trình Cách giải: \(\left\{ \begin{array}{l}x + y = 1\\2x + y = m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = m - 1\\x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = m - 1\\m - 1 + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = m - 1\\y = - m + 2\end{array} \right.\) Hệ phương trình có nghiệm duy nhất \(\left( {{x_0};{y_0}} \right) = \left( {m - 1; - m + 2} \right)\) Khi đó, \(P = x_0^2 + y_0^2 = {\left( {m - 1} \right)^2} + {\left( { - m + 2} \right)^2}\) \(\begin{array}{l} = {\left( {m - 1} \right)^2} + {\left( {m - 2} \right)^2}\\ = {m^2} - 2m + 1 + {m^2} - 4m + 4\\ = 2{m^2} - 6m + 5\\ = 2\left( {{m^2} - 3m + \dfrac{5}{2}} \right)\\ = 2\left[ {\left( {{m^2} - 2.\dfrac{3}{2}m + \dfrac{9}{4}} \right) - \dfrac{9}{4} + \dfrac{5}{2}} \right]\\ = 2\left[ {{{\left( {m - \dfrac{3}{2}} \right)}^2} + \dfrac{1}{2}} \right]\\ = 2{\left( {m - \dfrac{3}{2}} \right)^2} + 1\end{array}\) Ta có: \({\left( {m - \dfrac{3}{2}} \right)^2} \ge 0,\forall m\) nên \(2{\left( {m - \dfrac{3}{2}} \right)^2} + 1 \ge 1,\forall m\) hay \(P \ge 1,\forall m\) Dấu “=” xảy ra \( \Leftrightarrow m - \dfrac{3}{2} = 0 \Leftrightarrow m = \dfrac{3}{2}\) Vậy \(P\) đạt giá trị nhỏ nhất là \(1\) khi \(m = \dfrac{3}{2}\). Chọn D. Câu 6 Phương pháp: \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0\) Cách giải: Biểu thức \(\sqrt {x - 2} \) có nghĩa \( \Leftrightarrow x - 2 \ge 0 \Leftrightarrow x \ge 2\) Chọn D. Câu 7 Phương pháp: Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\) Thực hiện các phép tính với căn bậc hai. Cách giải: Ta có: \(\sqrt {25} + \sqrt 9 - \sqrt {36} \) \(\begin{array}{l} = \sqrt {{5^2}} + \sqrt {{3^2}} - \sqrt {{6^2}} \\ = 5 + 3 - 6\\ = 8 - 6\\ = 2\end{array}\) Chọn C. Câu 8 Phương pháp: Hệ phương trình \(\left\{ \begin{array}{l}ax + 2y = - 1\\bx - ay = 5\end{array} \right.\) có nghiệm là \(\left( {x;y} \right) = \left( {3; - 2} \right)\), nên ta có hệ phương trình là ẩn \(a\) và \(b\) Giải hệ phương trình đó, ta tìm được \(a\) và \(b\). Cách giải: Hệ phương trình \(\left\{ \begin{array}{l}ax + 2y = - 1\\bx - ay = 5\end{array} \right.\) có nghiệm là \(\left( {x;y} \right) = \left( {3; - 2} \right)\), nên ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\,\left\{ \begin{array}{l}a.3 + 2.\left( { - 2} \right) = - 1\\b.3 - a.\left( { - 2} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a - 4 = - 1\\3b + 2a = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3a = 3\\3b + 2a = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\3b + 2.1 = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 1\end{array} \right.\end{array}\) Vậy \(a = 1;b = 1\) Chọn D. Câu 9 Phương pháp: Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\) \(\dfrac{a}{{\sqrt {g\left( x \right)} }}\) \(\left( {a \in \mathbb{R}} \right)\) xác định \( \Leftrightarrow g\left( x \right) > 0\) Cách giải: \(\dfrac{1}{{\sqrt {6 - m} }}\) xác định \( \Leftrightarrow 6 - m > 0 \Leftrightarrow m < 6\) Hàm số \(y = \left( {m - 2} \right)x + \dfrac{1}{{\sqrt {6 - m} }}\) đồng biến \( \Leftrightarrow m - 2 > 0 \Leftrightarrow m > 2\) Kết hợp điều kiện: \(2 < m < 6\) Mà \(m\) là số nguyên nên \(m \in \left\{ {3;4;5} \right\}\) Vậy có \(3\) giá trị của \(m\) thỏa mãn. Chọn A. Câu 10 Phương pháp: Đường thẳng \(y = ax + b\) có hệ số góc là \(a\). Cách giải: Hệ số góc của đường thẳng \(y = \sqrt 5 x - 2\) là \(a = \sqrt 5 \) Chọn A. Câu 11 Phương pháp: Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a + b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = 1;{x_2} = \dfrac{c}{a}\) Cách giải: Ta có: \(1 + \left( { - 3} \right) + 2 = 0\) nên phương trình có hai nghiệm phân biệt \(x = 1;x = 2\) Vậy phương trình có tập nghiệm là \(S = \left\{ {1;2} \right\}\). Chọn D. Câu 12 Phương pháp: Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có nghiệm \( \Leftrightarrow \Delta = 0\) (hoặc \(\Delta ' = 0\)) Cách giải: Ta có: \(\Delta ' = {\left( { - 1} \right)^2} - m = 1 - m\) Phương trình có nghiệm \( \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow 1 - m \ge 0 \Leftrightarrow m \le 1\) Chọn C. Câu 13 Phương pháp: Kẻ tiếp tuyến \(ME\) của đường tròn \(\left( O \right)\)với \(E \in \left( O \right)\), tính được \(M{E^2}\). Chứng minh \(\Delta MEA \sim \Delta MBE\left( {g.g} \right) \Rightarrow MA.MB = M{E^2}\) từ đó tính được tích \(MA.MB\). Cách giải: Kẻ tiếp tuyến \(ME\) của đường tròn \(\left( O \right)\)với \(E \in \left( O \right)\) \( \Rightarrow \angle OEM = {90^0}\) \( \Rightarrow \Delta OEM\)vuông tại \(E\), theo định lý Py – ta – go, ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\,\,O{E^2} + M{E^2} = O{M^2}\\ \Leftrightarrow M{E^2} = {8^2} - {5^2}\\ \Leftrightarrow M{E^2} = 39\end{array}\) Xét \(\left( O \right)\) có: \(\angle EBA = \angle AEM\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn \(cungAE\)) Xét \(\Delta MEA\) và \(\Delta MBE\) có: \(\left. \begin{array}{l}\angle M\,\,chung\\\angle EBM = \angle EAM\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta MEA \sim \Delta MBE\left( {g.g} \right)\) \( \Rightarrow \dfrac{{MA}}{{ME}} = \dfrac{{ME}}{{MB}}\) (định nghĩa hai tam giác đồng dạng) \( \Rightarrow MA.MB = M{E^2} = 39\) Chọn C. Câu 14 Phương pháp: Sử dụng kiến thức: Số đo góc nội tiếp = \(\dfrac{1}{2}\)Số đo góc ở tâm cùng chắn một cung Áp dụng công thức tính diện tích hình quạt tròn có bán kính \(R\), cung \({n^0}\): \(S = \dfrac{{\pi {R^2}n}}{{360}}\) Diện tích phần gạch chéo \(S = {S_{quat\,AOB}} - {S_{\Delta OAB}}\) Cách giải: Xét \(\left( O \right)\) có: \(\angle ACB = \dfrac{1}{2}\angle AOB\) (do hai góc này cùng chắn \(cungAB\)) \( \Rightarrow \angle AOB = 2\angle ACB = {2.45^0} = {90^0}\) \( \Rightarrow \Delta AOB\) vuông tại \(O\) Khi đó, \({S_{\Delta AOB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.6.6 = 18\left( {c{m^2}} \right)\) \({S_{quatAOB}} = \dfrac{{\pi {{.6}^2}.90}}{{360}} = 9\pi \) Diện tích phần gạch chéo \(S = {S_{quat\,AOB}} - {S_{\Delta OAB}} = 9\pi - 18 = 9\left( {\pi - 2} \right)\,\,\left( {c{m^2}} \right)\) Chọn D. Câu 15 Phương pháp: Sử dụng định lý Py – ta – go. Cách giải: Tam giác \(ABC\) vuông tại \(A\), theo định lý Py – ta – go, ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\,A{C^2} + A{B^2} = B{C^2}\\ \Leftrightarrow {3^2} + A{B^2} = {5^2}\\ \Leftrightarrow A{B^2} = {5^2} - {3^2}\\ \Leftrightarrow A{B^2} = 16\\ \Rightarrow AB = 4\left( {cm} \right)\end{array}\) Chọn A. II. TỰ LUẬN: Câu 1: Phương pháp: 1) Sử dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình. 2) Xác định mẫu thức chung của biểu thức Thực hiện các phép toán với các phân thức đại số. 3) a) Thay \(m = - 5\), thay vào \(\left( 1 \right)\), biến đổi phương trình về dạng tích \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\) b) Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) \( \Leftrightarrow \Delta ' > 0\) Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}{x_2}\) Từ phương trình: \(x_1^2 + 4{x_1}{x_2} + 3x_2^2 = 0\), tìm được mối quan hệ của \({x_1}\) và \({x_2}\) Chia từng trường hợp, tìm được \(m\). Cách giải: 1) \(\left\{ \begin{array}{l}x - y = 4\\2x + y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = 4\\3x = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - 1\\x = 3\end{array} \right.\) Vậy hệ phương trình có tập nghiệm là \(\left( {x;y} \right) = \left( {3;\,\, - 1} \right)\). 2) Điều kiện: \(x > 0\), \(x \ne 1\) \(P = \left( {\dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{x + \sqrt x }}} \right):\dfrac{{\sqrt x - 1}}{{x + 2\sqrt x + 1}}\) \(\begin{array}{l}\,\,\,\, = \left( {\dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}}} \right):\dfrac{{\sqrt x - 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}}\\\,\,\, = \dfrac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)}}.\dfrac{{{{\left( {\sqrt x + 1} \right)}^2}}}{{\sqrt x - 1}}\end{array}\) \(\,\,\,\, = \dfrac{{\sqrt x + 1}}{{\sqrt x }}\) Vậy \(P = \dfrac{{\sqrt x + 1}}{{\sqrt x }}\) với \(x > 0\), \(x \ne 1\) 3) a) Với \(m = - 5\), thay vào \(\left( 1 \right)\), ta được: \(\begin{array}{l}\,\,\,\,\,\,{x^2} - 2x + \left( { - 5} \right) - 3 = 0\,\\ \Leftrightarrow {x^2} - 2x - 8 = 0\\ \Leftrightarrow {x^2} + 2x - 4x - 8 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - 4\left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x - 4} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 4 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 2\end{array} \right.\end{array}\) Vậy \(m = - 5\) thì phương trình đã cho có tập nghiệm: \(S = \left\{ { - 2;\,\,4} \right\}.\) b) Xét phương trình: \({x^2} - 2x + m - 3 = 0\,\,\left( 1 \right)\) Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) \( \Leftrightarrow \Delta ' > 0\) \(\begin{array}{l} \Leftrightarrow {\left( { - 1} \right)^2} - \left( {m - 3} \right) > 0\\ \Leftrightarrow 1 - m + 3 > 0\\ \Leftrightarrow 4 - m > 0\\ \Leftrightarrow m < 4\end{array}\) Vậy với \(m < 4\) phương trình có hai nghiệm phân biệt \({x_1},{x_2}\). Theo hệ thức Vi – ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\,\,\,\,\,\,\,\left( 2 \right)\\{x_1}.{x_2} = m - 3\,\,\,\left( 3 \right)\end{array} \right.\) Theo đề bài ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\,\,x_1^2 + 4{x_1}{x_2} + 3x_2^2 = 0\\ \Leftrightarrow \left( {x_1^2 + 4{x_1}{x_2} + 4x_2^2} \right) - x_2^2 = 0\\ \Leftrightarrow {\left( {{x_1} + 2{x_2}} \right)^2} - x_2^2 = 0\\ \Leftrightarrow \left( {{x_1} + 2{x_2} - {x_2}} \right)\left( {{x_1} + 2{x_2} + {x_2}} \right) = 0\\ \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left( {{x_1} + 3{x_2}} \right) = 0\end{array}\) \( \Leftrightarrow \left[ \begin{array}{l}{x_1} + {x_2} = 0\\{x_1} + 3{x_2} = 0\end{array} \right.\) TH1: \({x_1} + {x_2} = 0\) Kết hợp với phương trình \(\left( 2 \right)\) ta được hệ phương trình: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 0\\{x_1} + {x_2} = 2\end{array} \right. \Rightarrow \) hệ phương trình vô nghiệm. TH2: \({x_1} + 3{x_2} = 0\) Kết hợp với (2) ta có hệ phương trình \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\,\,\,\,\,\,\,\,\\\,{x_1} + 3{x_2} = 0\,\,\,\,\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 3\\{x_2} = - 1\end{array} \right.\) Thay \({x_1} = 3,{x_2} = - 1\) vào (3), ta được: \(\begin{array}{l}\,\,\,\,\,3.\left( { - 1} \right) = m - 3\\ \Leftrightarrow m - 3 = - 3\\ \Leftrightarrow m = 0\,\,\,\,\,\left( {tm} \right)\end{array}\) Vậy với \(m = 0\) thỏa mãn yêu cầu đề bài. Câu 2: Phương pháp: Gọi số máy thở mỗi nhà máy A sản suất theo kế hoạch là \(x\) (máy thở, \(x \in {\mathbb{N}^*}\)) Tính được thời gian nhà máy A sản xuất theo kế hoạch Tính được số máy thở và thời gian nhà máy A sản xuất trên thực tế Từ giả thiết, lập được phương trình, giải phương trình đối chiếu điều kiện và kết luận. Cách giải: Gọi số máy thở mỗi nhà máy A sản suất theo kế hoạch là \(x\) (máy thở, \(x \in {\mathbb{N}^*}\)) \( \Rightarrow \) Thời gian nhà máy A sản xuất máy thở theo kế hoạch là \(\dfrac{{300}}{x}\) (ngày) \( \Rightarrow \) Số máy thở nhà máy A sản xuất trên thực tế là \(x + 5\) (máy thở) \( \Rightarrow \) Thời gian nhà máy A sản xuất máy thở trên thực tế là \(\dfrac{{300}}{{x + 5}}\) (ngày) Vì thời gian hoàn thành công việc sớm hơn 10 ngày so với kế hoạch nên ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{{300}}{x} - \dfrac{{300}}{{x + 5}} = 10\\ \Rightarrow 30\left( {x + 5} \right) - 30x = x\left( {x + 5} \right)\\ \Leftrightarrow 30x + 150 - 30x = {x^2} + 5x\\ \Leftrightarrow {x^2} + 5x - 150 = 0\\ \Leftrightarrow {x^2} + 15x - 10x - 150 = 0\\ \Leftrightarrow x\left( {x + 15} \right) - 10\left( {x + 15} \right) = 0\end{array}\) \(\begin{array}{l} \Leftrightarrow \left( {x - 10} \right)\left( {x + 15} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 10 = 0\\x + 15 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 10\,\,\,\,\left( {tm} \right)\\x = - 15\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy số máy thở máy thở mỗi ngày nhà máy A sản xuất theo kế hoạch là \(10\) máy thở. Câu 3: Phương pháp: 1) Sử dụng dấu hiệu nhận biết: tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp. 2) + Ta sẽ chứng minh \(A,B,E,F,C\) cùng thuộc một đường tròn + Nối \(C\) với \(N\), kẻ đường kính \(AD\). Gọi \(I\) là giao điểm của \(AD\) và \(MN.\) Ta sẽ chứng minh: \(A{H^2} = AF.AC\) và \(A{N^2} = AC.AF\), từ đó có điều phải chứng minh. Cách giải:
1) Ta có: \(\begin{array}{l}AB \bot HE\,\,\,\left( {gt} \right) \Rightarrow AE \bot HE\,\,\,\left( {E \in AB} \right)\, \Rightarrow \angle AEH = {90^o}\\AC \bot HF\,\left( {gt} \right) \Rightarrow AF \bot HF\,\,\,\left( {F \in AC} \right) \Rightarrow \angle AFH = {90^o}\end{array}\) Suy ra \(\angle AEH + \angle AFH = {180^o}\) Mà \(\angle AEH\) và \(\angle AFH\) là hai góc đối nhau \( \Rightarrow \) Tứ giác \(AEHF\) nội tiếp trong một đường tròn (dấu hiệu nhận biết) (đpcm) (*) 2) Ta có: \(\angle AEF = \angle AHF\) (2 góc nội tiếp cùng chắn cung \(AF\)) Xét \(\Delta HFC\) vuông tại \(F\) ta có: \(\angle FCH + \angle FHC = {90^o}\) Mà \(AH \bot BC \Rightarrow \angle \,AHC = {90^o} \Rightarrow \angle AHF + \angle FHC = {90^O}\) Do đó \(\angle FCH = \angle AEF\) hay \(\angle AEF = \angle ACB\) Xét \(\Delta ABC\) và \(\Delta AFE\) ta có: \(\begin{array}{l}\angle BAC\,\,\,chung\\\angle AEF = \angle ACB\,\,\,\,\left( {cmt} \right)\end{array}\) \( \Rightarrow \Delta ABC\~\Delta AFE\,\,\left( {g - g} \right)\) \( \Rightarrow \angle ABC = \angle AFM\)(2 góc tương ứng) Lại có: \(\angle AEF = \angle ACH\,\)(cùng bằng \(\angle AHF\)) \(\begin{array}{l} \Rightarrow \angle AEF + \angle BEF = {180^o}\\ \Leftrightarrow \angle AEF + \angle ACH = {180^o}\end{array}\) Hay \(\angle AEF + \angle FCB = {180^o}\) Suy ra tứ giác \(BEFC\) nội tiếp một đường tròn (dấu hiệu nhận biết) (**) Từ (*) và (**) suy ra các điểm \(A,B,E,F,C\) cùng thuộc một đường tròn Mà \(\angle ABC = \angle AFM\) Nên số đo cung \(ABC\) bằng số đo cung \(AFM\) (đpcm) Nối \(C\) với \(N\), kẻ đường kính \(AD\). Gọi \(I\) là giao điểm của \(AD\) và \(MN.\) Ta có: \(\angle AEF = \angle AHF = \angle ACH = \angle ADB\) \( \Rightarrow \angle AEI + \angle EAI = \angle ADB + \angle BAD = {90^o}\) Suy ra \(\Delta AEI\) vuông tại \(I \Rightarrow AD \bot EF\) hay \(AD \bot MN\) tại \(I.\) Mà đường kính vuông góc với dây cung thì đi qua trung điểm của dây cung đó nên \(I\) là trung điểm của \(MN.\) \( \Rightarrow \Delta AMN\) cân tại \(A\) \( \Rightarrow \angle AMN = \angle ANM\) (tính chất) Ta có: \(\angle AMN = \angle ACN\) (2 góc nội tiếp cùng chắn cung \(AN\)) Suy ra \(\angle ACN = \angle ANM\) hay \(\angle ACN = \angle ANF\) Áp dụng hệ thức lượng trong \(\Delta AHC\) ta có: \(A{H^2} = AF.AC\) (1) Xét \(\Delta ANC\) và \(\Delta AFN\) ta có: \(\begin{array}{l}\angle NAC\,\,chung\\\angle ACN = \angle ANF\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta ANC\~\Delta AFN\,\,\,\left( {g - g} \right)\end{array}\) \( \Rightarrow \dfrac{{AN}}{{AF}} = \dfrac{{AC}}{{AN}}\) (cặp cạnh tương ứng tỉ lệ) \( \Rightarrow A{N^2} = AC.AF\) (2) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(AH = AN\) (đpcm). Câu 4 (VDC) Phương pháp: Ta có: \(A = \left( {a + b} \right)\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right) = 2 + \dfrac{a}{b} + \dfrac{b}{a}\) Đặt \(\dfrac{a}{b} = t\), tìm được điều kiện của \(t\) Thay \(\dfrac{a}{b} = t\) vào biểu thức \(A\), biến đổi khi đó ta có điều phải chứng minh. Cách giải: Ta có: \(A = \left( {a + b} \right)\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right) = 2 + \dfrac{a}{b} + \dfrac{b}{a}\) Đặt \(\dfrac{a}{b} = t\), khi đó \(1 \le a,b \le 2 \Rightarrow \dfrac{1}{2} \le t \le 2\) Suy ra \(\left( {t - 2} \right)\left( {t - \dfrac{1}{2}} \right) \le 0 \Rightarrow {t^2} + 1 \le \dfrac{5}{2}t\) \(A = 2 + t + \dfrac{1}{t} = 2 + \dfrac{{{t^2} + 1}}{t} \le 2 + \dfrac{{\dfrac{5}{2}t}}{t} = \dfrac{9}{2}\) Dấu bằng xảy ra \( \Leftrightarrow \left[ \begin{array}{l}t = 2\\t = \dfrac{1}{2}\end{array} \right.\,\, \Rightarrow \,\,\left[ \begin{array}{l}\left\{ \begin{array}{l}a = 2\\\,b = 1\end{array} \right.\\\left\{ \begin{array}{l}a = 1\\b = 2\end{array} \right.\end{array} \right..\) Vậy với \(1 \le a \le 2,\,\,\,1 \le b \le 2\) thì \(A \le \dfrac{9}{2}\).
|




















Danh sách bình luận