Đề thi vào 10 môn Toán Thái Nguyên năm 2023Tải vềCâu 1: Không sử dụng máy tính cầm tay, rút gọn biểu thức \(A = \sqrt 2 + \sqrt 8 - \sqrt {18} \) Câu 2: Không sử dụng máy tính cầm tay, giải phương trình \({x^2} - 3x + 2 = 0\) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
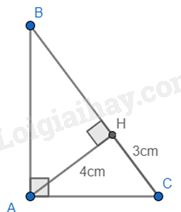
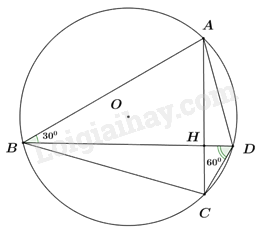
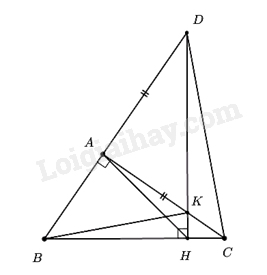
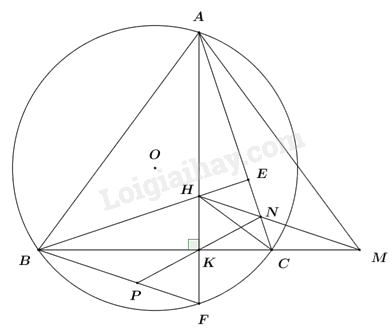
Đề bài Câu 1: Không sử dụng máy tính cầm tay, rút gọn biểu thức \(A = \sqrt 2 + \sqrt 8 - \sqrt {18} \) Câu 2: Không sử dụng máy tính cầm tay, giải phương trình \({x^2} - 3x + 2 = 0\) Câu 3: Không sử dụng máy tính cầm tay, giải hệ phương trình \(\left\{ \begin{array}{l}2x - 3y = 3\\2x + y = 7\end{array} \right.\) Câu 4: Cho hàm số bậc nhất \(y = 2x + m\), với m là tham số. a) Hàm số đã cho đồng biến hay nghịch biến trên \(\mathbb{R}\)? Vì sao? b) Tìm giá trị của m để đồ thị hàm số đã cho đi qua điểm A(1;3). Câu 5: Cho biểu thức \(B = \frac{x}{{\sqrt x + 2}} - \frac{4}{{\sqrt x }} + \frac{8}{{x + 2\sqrt x }},\) với x > 0. a) Rút gọn biểu thức B. b) Tính giá trị của biểu thức B khi \(x = 7 + 4\sqrt 3 \) Câu 6: Cho hình chữ nhật có chu vi bằng 30cm. Nếu chiều rộng tăng thêm 3cm và chiều dài giảm đi 1cm thì diện tích hình chữ nhật đó sẽ tăng thêm 18cm2. Tính chiều rộng và chiều dài của hình chữ nhật đã cho. Câu 7: Cho tam giác ABC vuông tại A có đường cao AH. Biết AH = 4cm và HC = 3cm. Tính độ dài các đoạn thẳng AC, BC và AB. Câu 8: Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi H là giao điểm của hai đường chéo AC và BD. Biết rằng \(\angle ABD = {30^0},\,\,\angle BDC = {60^0}\). Tính số đo của các cung nhỏ AD, BC và số đo của \(\angle BHC\). Câu 9: Cho tam giác ABC vuông tại A (AC > AB). Trên tia BA lấy điểm D sao cho AD = AC. Kẻ DH vuông góc với BC tại H. Gọi K là giao điểm của hai đường thẳng DH và AC. Chứng minh rằng: a) \(\angle DHA = \angle DCA\) b) \(AK = AB\) Câu 10: Cho tam giác ABC (AB > BC > CA) có ba góc nhọn nội tiếp đường tròn (O). Gọi điểm K là chân đường vuông góc kẻ từ điểm A đến cạnh BC và H là trực tâm của tam giác ABC. Gọi M là điểm đối xứng với điểm B qua điểm K. Gọi điểm N là giao điểm của hai đường thẳng HM và AC. a) Chứng minh rằng bốn điểm A, H, C, M cùng thuộc một đường tròn. b) Đường thẳng AH cắt đường tròn (O) tại điểm F \(\left( {F \ne A} \right)\). Gọi P là giao điểm của hai đường thẳng KN và BF. Chứng minh rằng NA.NC = NM.FP. -----HẾT----- Lời giải chi tiết Câu 1 (NB): Phương pháp: Khai căn bậc hai và rút gọn. Cách giải: Không sử dụng máy tính cầm tay, rút gọn biểu thức \(A = \sqrt 2 + \sqrt 8 - \sqrt {18} \) \(\begin{array}{l}A = \sqrt 2 + \sqrt 8 - \sqrt {18} \\\,\,\,\,\, = \sqrt 2 + \sqrt {{2^2}.2} - \sqrt {{3^2}.2} \\\,\,\,\,\, = \sqrt 2 + 2\sqrt 2 - 3\sqrt 2 \\\,\,\,\,\, = \sqrt 2 \left( {1 + 2 - 3} \right)\\\,\,\,\,\, = 0\end{array}\) Vậy A = 0. Câu 2 (NB): Phương pháp: Giải phương trình bằng cách nhẩm nghiệm. Cách giải: Ta có: \(a + b + c = 1 + \left( { - 3} \right) + 2 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = 1\\x = \frac{c}{a} = 2\end{array} \right.\). Vậy phương trình có tập nghiệm \(S = \left\{ {1;2} \right\}\). Câu 3 (NB): Phương pháp: Giải hệ phương trình bằng cách cộng đại số hoặc thế. Cách giải: \(\left\{ \begin{array}{l}2x - 3y = 3\\2x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4y = 4\\2x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\2x + 1 = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 3\end{array} \right.\) Vậy hệ phương trình có nghiệm duy nhất (x;y) = (3;1). Câu 4 (TH): Phương pháp: So sánh hệ số a với 0 để kết luận tính nghịch biến, đồng biến. Thay tọa độ A vào hàm số tìm m. Cách giải: a Hàm số đã cho đồng biến hay nghịch biến trên \(\mathbb{R}\)? Vì sao? Hàm số \(y = 2x + m\) đồng biến trên \(\mathbb{R}\) vì hệ số \(a = 2 > 0\). b, Tìm giá trị của m để đồ thị hàm số đã cho đi qua điểm A(1;3). Để đồ thị hàm số đã cho đi qua điểm A(1;3) \( \Leftrightarrow 3 = 2.1 + m\) \( \Rightarrow m = 3 - 2 = 1\). Vậy \(m = 1\) thì đồ thị hàm số đã cho đi qua điểm A(1;3). Câu 5 (TH): Phương pháp: a) Tìm mẫu số chung, quy động và rút gọn biểu thức b) Đưa x về dạng bình phương của tổng và thay vào B. Cách giải: a) Rút gọn biểu thức B. Với x > 0 ta có: \(\begin{array}{l}B = \frac{x}{{\sqrt x + 2}} - \frac{4}{{\sqrt x }} + \frac{8}{{x + 2\sqrt x }}\\\,\,\,\, = \frac{{x\sqrt x }}{{\sqrt x (\sqrt x + 2)}} - \frac{{4(\sqrt x + 2)}}{{\sqrt x (\sqrt x + 2)}} + \frac{8}{{\sqrt x (\sqrt x + 2)}}\\\,\,\,\, = \frac{{x\sqrt x - 4\sqrt x - 8 + 8}}{{\sqrt x (\sqrt x + 2)}}\\\,\,\,\, = \frac{{x\sqrt x - 4\sqrt x }}{{\sqrt x (\sqrt x + 2)}}\\\,\,\,\, = \frac{{\sqrt x (x - 4)}}{{\sqrt x (\sqrt x + 2)}}\\\,\,\,\, = \frac{{\sqrt x (\sqrt x - 2)(\sqrt x + 2)}}{{\sqrt x (\sqrt x + 2)}}\\\,\,\,\, = \sqrt x - 2\end{array}\) Vậy với x > 0 thì B = \(\sqrt x - 2\). b) Tính giá trị của biểu thức B khi \(x = 7 + 4\sqrt 3 \) Ta có: \(\begin{array}{l}x = 7 + 4\sqrt 3 \\\,\,\,\, = {2^2} + 2.2.\sqrt 3 + {\left( {\sqrt 3 } \right)^2}\\\,\,\,\, = {\left( {2 + \sqrt 3 } \right)^2}\\ \Rightarrow \sqrt x = \sqrt {{{\left( {2 + \sqrt 3 } \right)}^2}} = \left| {2 + \sqrt 3 } \right| = 2 + \sqrt 3 \,\,\left( {do\,\,2 + \sqrt 3 > 0} \right)\end{array}\) Thay \(\sqrt x = 2 + \sqrt 3 \) (tm ĐKXĐ) vào B ta có: \(B = 2 + \sqrt 3 - 2 = \sqrt 3 .\) Vậy với \(x = 7 + 4\sqrt 3 \)thì B = \(\sqrt 3 \). Câu 6 (TH): Phương pháp: Gọi chiều dài là x, biểu diễn chiều rộng, diện tích hình chữ nhật lúc đầu và lúc sau theo x và lập phương trình tìm x. Cách giải: Nửa chu vi hình chữ nhật là: \(30:2 = 15\,cm\). Gọi chiều dài hình chữ nhật là \(x\,\,(cm;\,\,0 < x < 15)\). \( \Rightarrow \) Chiều rộng hình chữ nhật là \(15 - x\,\)(cm). Diện tích hình chữ nhật là: \(x\left( {15 - x\,} \right)\,\,\left( {c{m^2}} \right)\). Nếu chiều rộng tăng thêm 3cm thì chiều rộng hình chữ nhật là: \(15 - x + 3 = 18 - x\) (cm). Nếu chiều dài giảm đi 1cm thì chiều dài hình chữ nhật là: \(x - 1\) (cm). Khi đó, diện tích hình chữ nhật lúc này là: \(\left( {18 - x} \right)\left( {x - 1} \right)\) \(\left( {c{m^2}} \right)\). Vì diện tích hình chữ nhật đó sẽ tăng thêm 18cm2 nên ta có phương trình: \(x\left( {15 - x\,} \right) + 18\, = \left( {18 - x} \right)\left( {x - 1} \right)\) \(\begin{array}{l} \Leftrightarrow 15x - {x^2} + 18 = 18x - 18 - {x^2} + x\\ \Leftrightarrow 4x = 36\\ \Rightarrow x = 9\,\,(TM)\end{array}\) Vậy chiều dài hình chữ nhật là 9cm, chiều rộng hình chữ nhật là \(15 - 9\, = 6\)cm. Câu 7 (TH): Phương pháp: Áp dụng hệ thức lượng trong tam giác vuông tính độ dài các đoạn thẳng AC, BC và AB. Cách giải:
Áp dụng định lí Pythagore vào tam giác vuông AHC, ta có: \(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} = {3^2} + {4^2} = 25\\ \Rightarrow AC = 5\,\,(cm)\end{array}\) Áp dụng hệ thức lượng trong tam giác vuông ABC, đường cao AH ta có: \(\begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\\ \Leftrightarrow \frac{1}{{A{B^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{C^2}}} = \frac{1}{{{4^2}}} - \frac{1}{{{5^2}}} = \frac{9}{{400}}\\ \Rightarrow A{B^2} = \frac{{400}}{9} = > AB = \frac{{20}}{3}(cm)\end{array}\) Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có: \(A{B^2} + A{C^2} = B{C^2} \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{\left( {\frac{{20}}{3}} \right)}^2} + {5^2}} = \frac{{25}}{3}\) (cm) Vậy AC = 5cm, BC = \(\frac{{25}}{3}\)cm và AB = \(\frac{{20}}{3}\)cm Câu 8 (TH): Phương pháp: Sử dụng mối liên hệ góc nội tiếp, số đo các cung để tính. Cách giải:
+) Tính số đo của cung nhỏ AD Ta có: \(\angle ABD\) nội tiếp chắn cung nhỏ AD \( \Rightarrow \angle ABD = \frac{1}{2}\) số đo cung nhỏ AD \( \Rightarrow {30^0}\) \( = \frac{1}{2}\)số đo cung nhỏ AD \( \Rightarrow \) số đo cung nhỏ AD \( = {60^0}\). +) Tính số đo của cung nhỏ BC Ta có: \(\angle BDC\) nội tiếp chắn cung nhỏ BC \( \Rightarrow \angle BDC = \frac{1}{2}\) số đo cung nhỏ BC \( \Rightarrow {60^0}\) \( = \frac{1}{2}\)số đo cung nhỏ BC \( \Rightarrow \) số đo cung nhỏ BC \( = {120^0}\). +) Tính số đo của góc BHC. Góc BHC là góc có đỉnh ở bên trong đường tròn, chắn hai cung nhỏ AD và BD \( \Rightarrow \angle BHC = \frac{1}{2}\)(số đo cung nhỏ AD + số đo cung nhỏ BC) \( \Rightarrow \angle BHC = \frac{1}{2}\left( {{{60}^0} + {{120}^0}} \right) = \frac{1}{2}{.180^0} = {90^0}\). Vậy \(\angle BHC = {90^0}\). Câu 9 (TH): Phương pháp: a) Chứng minh tứ giác nội tiếp từ đó suy ra các góc nội tiếp bằng nhau b) Chứng minh \(\angle AKB = \angle ABK \Rightarrow \Delta AKB\) cân tại A. Cách giải:
a) \(\angle DHA = \angle DCA\) Ta có \(\angle DAC = \angle DHC = {90^0}\) (do tam giác ABC vuông tại A và \(DH \bot BC\) tại H) Mà A, H là 2 đỉnh kề nhau, cùng nhìn DC dưới 2 góc bằng nhau nên AHCD nội tiếp \( \Rightarrow \angle DHA = \angle DAC\) (hai góc nội tiếp cùng chắn cung AD) (đpcm) b) \(AK = AB\) Do AD = AC (giá trị) nên tam giác ACD cân tại A \( \Rightarrow \angle ADC = \angle ACD\) (tính chất) (1) Xét tứ giác AKHB có \(\angle BAK = \angle AHK = {90^0} \Rightarrow \angle BAK + \angle AHK = {90^0} + {90^0} = {180^0}\) Suy ra tứ giác AKHB nội tiếp (tổng hai góc đối bằng \({180^0}\)) (đhnb) \( \Rightarrow \angle AKB = \angle AHB\) (hai góc nội tiếp cùng chắn cung AB) Mà \(\angle AHB = \angle BDC\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp AHCD) \( \Rightarrow \angle AKB = \angle BDC = \angle ADC\) (2) Ta có \(\angle ABK = \angle AHK\) (hai góc nội tiếp cùng chắn cung AK) Mà \(\angle AHK = \angle AHD = \angle ACD\) (hai góc nội tiếp cùng chắn cung AD) \( \Rightarrow \angle ABK = \angle ACD\) (3) Từ (1), (2), (3) suy ra \(\angle AKB = \angle ABK \Rightarrow \Delta AKB\) cân tại A. Vậy AK = AB (tính chất tam giác cân) (đpcm). Câu 10 (TH): Phương pháp: a) Chứng minh hai đỉnh cùng nhìn cạnh dưới 2 góc bằng nhau. b) Chứng minh các tam giác đồng dạng để suy ra tỉ lệ Cách giải:
a) Chứng minh rằng bốn điểm A, H, C, M cùng thuộc một đường tròn. Vì M đối xứng với B qua K nên BK = MK. Xét \(\Delta HBK\) và \(\Delta HMK\) có: \(\begin{array}{l}HK\,\,chung\\\angle HKB = \angle HKM = {90^0}\,\,\left( {gt} \right)\\BK = MK\,\,\left( {cmt} \right)\end{array}\) \( \Rightarrow \Delta HBK = \Delta HMK\) (hai cạnh góc vuông). \( \Rightarrow HB = HM\) (2 góc tương ứng) \( \Rightarrow \Delta HBM\) cân tại H (định nghĩa) \( \Rightarrow \angle HBM = \angle HMB\) (tính chất tam giác cân) (1) Kéo dài BH cắt AC tại E. Vì H là trực tâm của tam giác ABC (gt) \( \Rightarrow BE \bot AC \Rightarrow \Delta BCE\) vuông tại C. Ta có: \(\angle HBM + \angle BCE = {90^0}\) (tam giác BCE vuông tại C). \(\angle HAC + \angle BCE = {90^0}\) (tam giác ACK vuông tại K). \( \Rightarrow \angle HBM = \angle HAC\) (2) Từ (1) và (2) \( \Rightarrow \angle HMB = \angle HAC \Rightarrow \angle HMC = \angle HAC\). Mà 2 đỉnh A, M kề nhau cùng nhìn HC dưới hai góc bằng nhau. \( \Rightarrow AHCM\) là tứ giác nội tiếp (dhnb). Vậy bốn điểm A, H, C, M cùng thuộc một đường tròn (đpcm). b) Đường thẳng AH cắt đường tròn (O) tại điểm F \(\left( {F \ne A} \right)\). Gọi P là giao điểm của hai đường thẳng KN và BF. Chứng minh rằng NA.NC = NM.FP. Ta có: \(\angle HBM = \angle HAC\) (cmt) \( \Rightarrow \angle HBK = \angle FAC\). Mà \(\angle FAC = \angle FBC = \angle FBK\) (hai góc nội tiếp cùng chắn cung FC). \( \Rightarrow \angle HBK = \angle FBK\). Xét tam giác vuông BHK và tam giác vuông BFK có: \(\begin{array}{l}\angle BKH = \angle BKF = {90^0}\\BK\,\,chung\\\angle HBK = \angle FBK\,\,\left( {cmt} \right)\end{array}\) \( \Rightarrow \Delta BHK = \Delta BFK\) (cạnh góc vuông – góc nhọn kề). \( \Rightarrow HK = FK\) (hai cạnh tương ứng) và \(\angle BHK = \angle BFK\) (hai góc tương ứng). Ta có: \(\Delta HBK = \Delta HMK\,\,\left( {cmt} \right) \Rightarrow \angle BHK = \angle MHK\) (hai góc tương ứng). \( \Rightarrow \angle BFK = \angle MHK \Rightarrow \angle PFK = \angle NHK\). Xét \(\Delta PFK\) và \(\Delta NHK\) có: \(\begin{array}{l}FK = HK\,\,\left( {cmt} \right)\\\angle PFK = \angle NHK\,\,\left( {cmt} \right)\end{array}\) \(\angle FKP = \angle HKN\) (đối đỉnh) \( \Rightarrow \Delta PFK = \Delta NHK\,\,\left( {g.c.g} \right) \Rightarrow FP = NH\) (hai cạnh tương ứng). Xét \(\Delta NAH\) và \(\Delta NMC\) có: \(\angle ANH = \angle MNC\) (đối đỉnh) \(\angle NAH = \angle NMC\) (hai góc nội tiếp cùng chắn cung HC của tứ giác nội tiếp AHCM). $\Rightarrow \Delta NAH\backsim \Delta NMC\,\,\left( g.g \right)$ \( \Rightarrow \frac{{NA}}{{NM}} = \frac{{NH}}{{NC}}\) (cặp cạnh tương ứng tỉ lệ). \( \Rightarrow NA.NC = NM.NH\). Mà NH = FB (cmt). Vậy NA.NC = NM.FP (đpcm).
|




















Danh sách bình luận