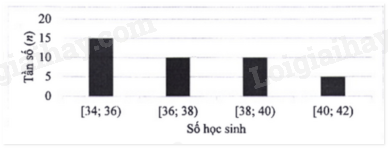
Đề thi vào 10 môn toán có đáp án - 9 năm gần nhất

Đề thi minh hoạ vào 10 môn Toán Hà Nội năm 2025

Tải về

Sau khi điều tra số học sinh trong 40 lớp học (đơn vị: học sinh), người ta có biểu đồ tần số ghép nhóm dưới đây: Tìm tần số ghép nhóm và tần số tương đối ghép nhóm [40; 42).

Quảng cáo

Lựa chọn câu để xem lời giải nhanh hơn

Tải về

Đề bài

Câu 1:

1) Sau khi điều tra số học sinh trong 40 lớp học (đơn vị: học sinh), người ta có biểu đồ tần số ghép nhóm dưới đây:

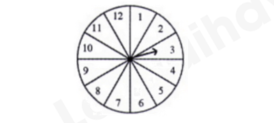
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm [40; 42).

2) Hình vẽ dưới đây mô tả một đĩa tròn bằng bìa cứng được chia làm 12 phần bằng nhau và ghi các số 1, 2, 3, …, 11, 12; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.

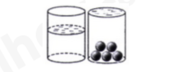
Xét phép thử “Quay đĩa tròn một lần” và biến cố M: “Chiếc kim chỉ vào hình quạt ghi số chia hết cho 4”. Tính xác suất của biến cố M.

Câu 2: Cho hai biểu thức: $A = \frac{{x - 4}}{{\sqrt x }}$ và $B = \frac{3}{{\sqrt x {\rm{ \;}} - 2}} + \frac{{2\sqrt x {\rm{ \;}} + 3}}{{4 - x}}$ với $x > 0,x \ne 4$.

1) Tính giá trị của biểu thức $A$ khi $x = 9$.

2) Chứng minh $B = \frac{{\sqrt x {\rm{ \;}} + 3}}{{x - 4}}$.

3) Xét biểu thức $P = AB$. Chứng minh $P < {P^2}$.

Câu 3:

1) Bác Tiến chia số tiền 400 triệu đồng của mình cho hai khoản đầu tư. Sau một năm tổng số tiền lãi thu được là 27 triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là $6\% $/năm và khoản đầu tư thứ hai là $8\% $/năm. Tính số tiền bác Tiến đầu tư cho mỗi khoản.

2) Một tổ sản xuất có kế hoạch làm 300 sản phẩm cùng loại trong một số ngày quy định. Thực tế, mỗi ngày tổ đã làm được nhiều hơn 10 sản phẩm so với số sản phẩm dự định làm trong một ngày theo kế hoạch. Vì thế tổ đã hoàn thành công việc sớm hơn kế hoạch 1 ngày. Hỏi theo kế hoạch, mỗi ngày tổ sản xuất phải làm bao nhiêu sản phẩm? (Giả định rằng số sản phầm mà tổ đó làm được trong mỗi ngày là bằng nhau).

3) Biết rằng phương trình bậc hai ${x^2} - 3x + a = 0$ có một nghiệm là $x = \frac{{3 - \sqrt 5 }}{2}$. Tìm tổng bình phương hai nghiệm của phương trình trên.

Câu 4:

1) Một ly nước dạng hình trụ có chiều cao 15cm, đường kính đáy là 5cm, lượng nước tinh khiết trong ly cao 10cm. Ly nước được đặt cố định trên mặt bàn bằng phẳng như hình vẽ dưới đây.

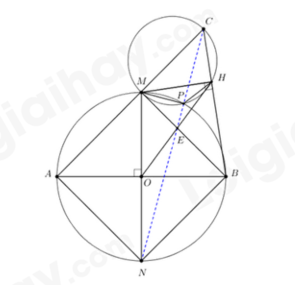
a) Tính thể tích nước tinh khiết được chứa trong ly.

b) Người ta thả vào ly nước 5 viên bi hình cầu giống hệt nhau, có cùng thể tích, đồng chất và ngập hoàn toàn trong nước, làm nước trong ly dâng lên đúng bằng miệng ly, không tràn ra ngoài. Hỏi thể tích của mỗi viên bi là bao nhiêu xăng-ti-mét khối? (Giả sử độ dày của ly là không đáng kể)

2) Cho đường tròn (O) có hai đường kính AB và MN vuông góc với nhau. Trên tia đối của tia MA lấy điểm C khác điểm M. Gọi H là chân đường vuông góc kẻ từ điểm M đến đường thẳng BC.

a) Chứng minh bốn điểm O, M, H, B cùng thuộc một đường tròn.

b) Hai đường thẳng MB và OH cắt nhau tại E. Chứng minh $\angle MHO = \angle MNA$ và $ME \cdot MH = BE \cdot HC$.

c) Gọi P là giao điểm thứ hai của đường tròn (O) và đường tròn ngoại tiếp tam giác MHC. Chứng minh ba điểm C, P, E là ba điểm thẳng hàng.

Câu 5: Trong buổi thăm quan dã ngoại, mỗi lớp khối $9$ được chuẩn bị một tấm bạt hình chữ nhật ABCD cùng loại, có chiều dài 10m và chiều rộng 6m; với M,N lần lượt là trung điểm của AD,BC (hình 1)

Mỗi lớp sử dụng tấm bạt nhựa trên để dựng thành chiếc lều có dạng hình lăng trụ đứng tam giác (hình 2); hai đáy hình lăng trụ là hai tam giác cân AMD và tam giác BMC, với độ dài cạnh đáy của tam giác cân này là $x\left( m \right)$. (Tấm bạt chỉ sử dụng để dụng thành hai mái lều, không trải thành đáy lều). Tìm $x$ để thể tích không gian trong lều là lớn nhất.

----- HẾT -----

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM

Câu 1 (TH):

Cách giải:

1) - Quan sát biểu đồ tần số ghép nhóm, ta thấy tần số ghép nhóm của nhóm [40; 42) là 5.

- Tần số tương đối ghép nhóm của nhóm [40;42) là: $f = \frac{5}{{40}}.100\% {\rm{ \;}} = 12,5\% $

2) Có 12 kết quả có thể của phép thử “Quay đĩa tròn một lần” là: 1, 2, 3, …, 11, 12.

Có 3 kết quả thuận lợi cho biến cố M: “Chiếc kim chỉ vào hình quạt ghi số chia hết cho 4” là: 4; 8; 12.

Vậy xác suất của biến cố M là: $\frac{3}{{12}} = \frac{1}{4}$.

Câu 2 (VD):

Cách giải:

1) Thay $x = 9$ (TMĐK) vào biểu thức A, ta được:

$A = \frac{{x - 4}}{{\sqrt x }} = \frac{{9 - 4}}{{\sqrt 9 }} = \frac{5}{3}$

Vậy $A = \frac{5}{3}$ khi $x = 9$

2) ĐKXĐ: $x > 0,x \ne 4$

$B = \frac{3}{{\sqrt x {\rm{ \;}} - 2}} + \frac{{2\sqrt x {\rm{ \;}} + 3}}{{4 - x}}$

$B = \frac{3}{{\sqrt x {\rm{ \;}} - 2}} - \frac{{2\sqrt x {\rm{ \;}} + 3}}{{x - 4}}$

$B = \frac{{3(\sqrt x {\rm{ \;}} + 2)}}{{(\sqrt x {\rm{ \;}} - 2)(\sqrt x {\rm{ \;}} + 2)}} - \frac{{2\sqrt x {\rm{ \;}} + 3}}{{(\sqrt x {\rm{ \;}} - 2)(\sqrt x {\rm{ \;}} + 2)}}$

$B = \frac{{3\sqrt x {\rm{ \;}} + 6 - 2\sqrt x {\rm{ \;}} - 3}}{{(\sqrt x {\rm{ \;}} - 2)(\sqrt x {\rm{ \;}} + 2)}}$

$B = \frac{{\sqrt x {\rm{ \;}} + 3}}{{x - 4}}$

Vậy $B = \frac{{\sqrt x {\rm{ \;}} + 3}}{{x - 4}}$ với $x > 0,x \ne 4$

3) ĐKXĐ: $x > 0,x \ne 4$

$P = AB = \frac{{x - 4}}{{\sqrt x }} \cdot \frac{{\sqrt x {\rm{ \;}} + 3}}{{x - 4}} = \frac{{\sqrt x {\rm{ \;}} + 3}}{{\sqrt x }}$

Xét hiệu $P - 1 = \frac{{\sqrt x {\rm{ \;}} + 3}}{{\sqrt x }} - 1 = \frac{{\sqrt x {\rm{ \;}} + 3 - \sqrt x }}{{\sqrt x }} = \frac{3}{{\sqrt x }}$

Ta có: ${P^2} - P = P(P - 1)$

Vì $x > 0$ nên $\sqrt x {\rm{ \;}} > 0$ và $\sqrt x {\rm{ \;}} + 3 > 0$

Khi đó $\frac{{\sqrt x {\rm{ \;}} + 3}}{{\sqrt x }} > 0$ và $\frac{3}{{\sqrt x }} > 0$ hay $P > 0$ và $P - 1 > 0$

Suy ra $P(P - 1) > 0$ hay ${P^2} - P > 0$

Vậy $P < {P^2}$ với $x > 0,x \ne 4$

Câu 3 (TH):

Cách giải:

1) Gọi số tiền đầu tư cho mỗi khoản lần lượt là $x,y(0 < x,y < 400)$.

Tổng số tiền đầu tư là 400 triệu, nên ta có phương trình: $x + y = 400$ (1)

Số tiền lãi thu được sau 1 năm của hai khoản đầu tư là: $0,06x + 0,08y = 27$ (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{ {\begin{array}{*{20}{l}}{x + y = 400}\\{0,06x + 0,08y = 27}\end{array}} \right.$ suy ra $\left\{ {\begin{array}{*{20}{l}}{x = 250}\\{y = 150}\end{array}} \right.{\mkern 1mu} {\mkern 1mu} (tm)$

Vậy số tiền đầu tư cho hai khoản lần lượt là 250 triệu đồng và 150 triệu đồng.

2) Gọi số sản phẩm cần làm trong một ngày theo kế hoạch là $x(x < 300;x \in {\mathbb{N}^*})$, số ngày hoàn thành theo kế hoạch là $y(y > 1).$

Theo kế hoạch, ta có $xy = 300$.

Thực tế mỗi ngày làm thêm 10 sản phẩm và hoàn thành công việc sớm 1 ngày nên ta có: $(x + 10)(y - 1) = 300$

Ta có hệ phương trình:

$\left\{ {\begin{array}{*{20}{l}}{xy = 300\$ x + 10)(y - 1) = 300}\end{array}} \right.$

$\left\{ {\begin{array}{*{20}{l}}{xy = 300}\\{ - x + 10y = 10}\end{array}} \right.$

Suy ra $\left\{ {\begin{array}{*{20}{l}}{x = 50}\\{y = 6}\end{array}} \right.{\mkern 1mu} {\mkern 1mu} (tm)$

Vậy theo kế hoạch, mỗi ngày tổ sản xuất phải làm 50 sản phẩm.

3) ${x^2} - 3x + a = 0$ có nghiệm $x = \frac{{3 - \sqrt 5 }}{2}$ nên ta thay $x = \frac{{3 - \sqrt 5 }}{2}$ vào phương trình:

$\begin{array}{*{20}{l}}{{{\left( {\frac{{3 - \sqrt 5 }}{2}} \right)}^2} - 3.\left( {\frac{{3 - \sqrt 5 }}{2}} \right) + a = 0}\\{\frac{{7 - 3\sqrt 5 }}{2} - \frac{{9 - 3\sqrt 5 }}{2} + a = 0}\\{a = 1.}\end{array}$

Phương trình: ${x^2} - 3x + 1 = 0$

Theo định lí Viète ta có: $\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 3}\\{{x_1}{x_2} = 1}\end{array}} \right.$

Tổng bình phương 2 nghiệm $x_1^2 + x_2^2 = {({x_1} + {x_2})^2} - 2{x_1}{x_2} = 9 - 2 = 7.$

Câu 4 (VD):

Cách giải:

a) Bán kính của ly nước là

$5:2 = 2,5\left( {cm} \right)$

Thể tích nước tinh khiết chứa trong ly là:

$V = \pi .2,{5^2}.10 = 62,5\pi \left( {c{m^3}} \right)$

Vậy thể tích nước tinh khiết được chứa trong ly là $62,5\pi $$c{m^3}$.

b) Thể tích của 5 viên bi hình cầu là:

$V = \pi .2,{5^2}.\left( {15 - 10} \right) = 31,25\pi \left( {c{m^3}} \right)$

Thể tích của mỗi viên bi là:

$31,25\pi :5 = 6,25\pi \left( {c{m^3}} \right)$

Vậy thể tích của mỗi viên bi là $6,25\pi $$c{m^3}$.

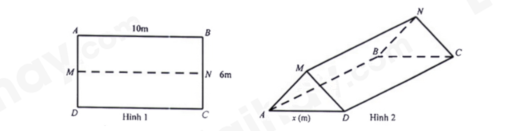
a) Chứng minh bốn điểm O, M, H, B cùng thuộc một đường tròn.

Do $AB \bot MN$ nên $\Delta MOB$ vuông tại O, cạnh huyền MB

Suy ra M, O, B cùng thuộc đường tròn đường kính MB

Tương tự $\Delta MHB$ vuông tại H, cạnh huyền MB nên M, H, B cùng thuộc đường tròn đường kính MB

Vậy O, M, B, H cùng thuộc đường tròn đường kính MB (đpcm)

b) Hai đường thẳng MB và OH cắt nhau tại E. Chứng minh $\angle MHO = \angle MNA$ và $ME \cdot MH = BE \cdot HC$.

Do O, M, B, H cùng thuộc đường tròn nên MOBH nội tiếp đường tròn

Suy ra $\angle MHO = \angle MBO$ (hai góc nội tiếp cùng chắn cung MO)

Mà $\angle MNA = \angle MBA$ (hai góc nội tiếp cùng chắn cung MA của (O))

Suy ra $\angle MHO = \angle MNA$ (đpcm)

Ta có $\angle AMB = \frac{1}{2}sđAB = {90^0}$ nên $\angle BMC = {90^0}$

Do $\angle CMH + \angle HMB = \angle CMB = {90^0}$ kết hợp với $\angle HBM + \angle HMB = {180^0} - \angle MHB = {90^0}$

Nên $\angle CMH = \angle HBM$

Xét $\Delta MHC$ và $\Delta BHM$ có $\angle CMH = \angle HBM$

$\angle CHM = \angle BHM\left( { = {{90}^0}} \right)$

Suy ra $\Delta MHC \backsim \Delta BHM\left( {g.g} \right)$

Suy ra $\frac{{HC}}{{HM}} = \frac{{MH}}{{HB}}$ (1)

Vì MO = OB nên tam giác MOB cân tại O suy ra $\angle OMB = \angle OBM$ (tính chất)

Tứ giác MHBO nội tiếp đường tròn đường kính MB nên ta có:

$\angle MHO = \angle MBO;{\mkern 1mu} {\mkern 1mu} \angle OHB = \angle OMB$ (các góc nội tiếp cùng chắn một cung)

Khi đó $\angle MHO = \angle OHB$

Suy ra EH là phân giác của góc MHB

Suy ra $\frac{{ME}}{{EB}} = \frac{{MH}}{{HB}}$ (tính chất đường phân giác) (2)

Từ (1) và (2) suy ra $\frac{{HC}}{{HM}} = \frac{{ME}}{{EB}}$ hay $HC.EB = HM.ME$ (đpcm)

c) Gọi P là giao điểm thứ hai của đường tròn (O) và đường tròn ngoại tiếp tam giác MHC. Chứng minh ba điểm C, P, E là ba điểm thẳng hàng.

Ta có $\Delta CHM$ vuông tại H nên C, H, M cùng thuộc đường tròn đường kính CM

Mà $P$ thuộc đường tròn đường kính CM nên $\angle MPC = {90^0}$ hay $MP \bot PC$

Tương tự P thuộc đường tròn (O), đường kính MN nên $\angle MPN = {90^0}$ hay $MP \bot PN$

Suy ra C, P, N thẳng hàng (*)

Xét $\Delta MHC$ và $\Delta BMC$ có $\angle CHM = \angle CMB = {90^0}$

$\angle BCM$ chung

Nên $\Delta MHC \backsim \Delta BMC\left( {g.g} \right)$

Suy ra $\frac{{HC}}{{MC}} = \frac{{MH}}{{MB}}$ hay $\frac{{HC}}{{MH}} = \frac{{MC}}{{MB}}$

Mà $\frac{{HC}}{{HM}} = \frac{{ME}}{{EB}}$ suy ra $\frac{{MC}}{{MB}} = \frac{{ME}}{{EB}}$ (3)

Ta có $\Delta BMN$ có BO vừa là trung tuyến vừa là đường cao nên $\Delta BMN$ cân tại B

Suy ra $BM = BN$

Thay vào (3) ta được $\frac{{MC}}{{BN}} = \frac{{ME}}{{EB}}$

Xét $\Delta MEC$ và $\Delta BEN$ có $\frac{{MC}}{{BN}} = \frac{{ME}}{{EB}}$ và $\angle EMC = \angle EBN\left( { = {{90}^0}} \right)$

Suy ra $\Delta MEC \backsim \Delta BEN\left( {c.g.c} \right)$

Suy ra $\angle MEC = \angle BEN$ (hai góc tương tứng)

Mà $\angle MEC + \angle CEB = {180^0}$ (hai góc kề bù) nên $\angle BEN + \angle CEB = {180^0}$

Chứng tỏ C, E, N thẳng hàng (**)

Từ (*) và (**) suy ra C, P, E thẳng hàng (đpcm).

Câu 5 (VD):

Cách giải:

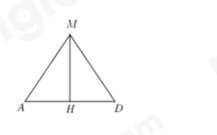
Thể tích không gian trong lều là: $V = {S_{AMD}}.AB = 10{S_{AMD}}.$

Để thể tích không gian trong lều là lớn nhất thì ${S_{AMD}}$ lớn nhất.

Kẻ $MH \bot AD{\mkern 1mu} \left( {H \in AD} \right)$

Ta có: $AM = MD = \frac{6}{2} = 3m.$

Do $\Delta AMD$ cân tại $M$ có MH là đường cao đồng thời là đường trung tuyến nên $H$ là trung điểm của AD. Do đó $AH = \frac{{AD}}{2} = \frac{x}{2}.$

Áp dụng định lý Phythagore cho tam giác MAH vuông tại $H$, ta có:

$M{H^2} = A{M^2} - A{H^2} = {3^2} - {\left( {\frac{x}{2}} \right)^2} = \frac{{36 - {x^2}}}{4}$

Suy ra: $MH = \frac{{\sqrt {36 - {x^2}} }}{2}.$ Điều kiện $0 < x < 6$

Ta có: ${S_{AMD}} = \frac{1}{2}AD.MH = \frac{1}{4}x\sqrt {36 - {x^2}} $

Để ${S_{AMD}}$ lớn nhất thì ${({S_{AMD}})^2}$ lớn nhất.

${({S_{AMD}})^2} = \frac{1}{{16}}{x^2}(36 - {x^2}) \le \frac{1}{{16}}{\left( {\frac{{{x^2} + 36 - {x^2}}}{2}} \right)^2} = \frac{{81}}{4}$ (BĐT cô-si)

Dấu bằng xảy ra khi ${x^2} = 36 - {x^2}$ hay ${x^2} = 18$ hay $x = 3\sqrt 2 $ (Do $x > 0$)

Vậy với $x = 3\sqrt 2 $ thì thể tích không gian trong lều đạt giá trị lớn nhất.