Đề thi vào 10 môn Toán Vĩnh Long năm 2020Tải vềBài 1: Tính giá trị biểu thức: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
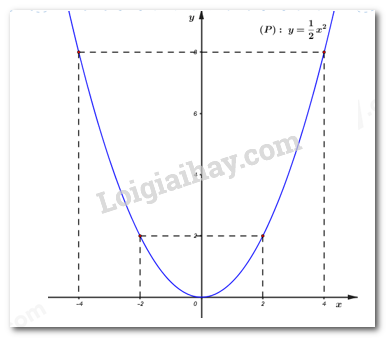
Đề bài Bài 1: Tính giá trị biểu thức: a) \(A = 2\sqrt {20} + 3\sqrt {45} - \sqrt {80} \) b) \(B = \sqrt {{{\left( {3 - \sqrt 7 } \right)}^2}} + \sqrt {11 + 4\sqrt 7 } \) Bài 2: Giải các phương trình và hệ phương trình sau: a) \(3{x^2} - 7x + 4 = 0\). b) \(3{x^2} - 12 = 0\) b) \(3{x^2} - 12 = 0\) d) \({x^4} - 4{x^2} + 4 = 0\) Bài 3: a) Trong mặt phẳng tọa độ \(Oxy,\) cho hàm số \(y = \dfrac{1}{2}{x^2}\) có đồ thị \(\left( P \right).\) Vẽ đồ thị \(\left( P \right).\) b) Cho phương trình \({x^2} + \left( {2m - 5} \right)x + 4 - 2m = 0\) (\(x\) là ẩn số, \(m\) là tham số). Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^3 + x_2^3 = 1.\) Bài 4: Một người dự định đi xe máy từ Vĩnh Long đến Sóc Trăng cách nhau 90 km. Vì có việc gấp cần đến Sóc Trăng trước giờ dự định 27 phút, nên người ấy phải tăng vận tốc thêm 10 km/h. Hãy tính vận tốc xe máy mà người đó dự định đi. Bài 5: Cho tam giác \(ABC\) vuông tại \(A\) , đường cao AH. Biết \(BH = 4cm,{\rm{ }}CH = 9cm\) a) Tính độ dài đường cao AH và số đo \(\angle ABH\) (làm tròn đến độ) b) Vẽ đường trung tuyến AM của tam giác ABC \(\left( {M \in BC} \right)\) , tính diện tích tam giác \(AHM.\) Bài 6: Cho nửa đường tròn tâm O đường kính AB. Vẽ đường thẳng \(d\) vuông góc với OA tại M \(\left( {M \ne O,A} \right)\). Trên \(d\) lấy điểm N sao cho N nằm bên ngoài nửa đường tròn \(\left( O \right)\). Kẻ tiếp tuyến \(NE\) với nửa đường tròn \(\left( O \right)\) (E là tiếp điểm, E và A nằm cùng phía đối với đường thẳng \(d\)) a) Chứng minh tứ giác OMEN nội tiếp được đường tròn. b) Nối NB cắt nửa đường tròn (O) tại C. Chứng minh \(N{E^2} = NC.NB\). c) Gọi H là giao điểm của AC và \(d\), F là giao điểm của tia EH và nửa đường tròn (O). Chứng minh \(\angle NEF = \angle NOF\) Bài 7: Cho hai phương trình \({x^2} + \left( {2{m^2} + 1} \right)x + {m^3} + 7\sqrt 2 - 23 = 0\,\,\,\left( 1 \right)\) và \(2{x^2} + \left( {{m^2} - m} \right)x + 9\sqrt 2 - 30 = 0\,\,\,\left( 2 \right)\) (\(x\) là ẩn số, \(m\) là tham số). Tìm giá trị của tham số \(m\) để phương trình (1) và phương trình (2) có nghiệm chung \(x = 3\). Lời giải Bài 1. (1,0 điểm) Cách giải: Tính giá trị biểu thức: a) \(A = 2\sqrt {20} + 3\sqrt {45} - \sqrt {80} \) \(\begin{array}{l} \Leftrightarrow A = 2\sqrt {{2^2}.5} + 3\sqrt {{3^2}.5} - \sqrt {{4^2}.5} \\ \Leftrightarrow A = 2.2\sqrt 5 + 3.3\sqrt 5 - 4\sqrt 5 \\ \Leftrightarrow A = 4\sqrt 5 + 9\sqrt 5 - 4\sqrt 5 \\ \Leftrightarrow A = 9\sqrt 5 \end{array}\) Vậy \(A = 9\sqrt 5 \). b) \(B = \sqrt {{{\left( {3 - \sqrt 7 } \right)}^2}} + \sqrt {11 + 4\sqrt 7 } \) \(\begin{array}{l} \Leftrightarrow B = \left| {3 - \sqrt 7 } \right| + \sqrt {{{\left( {\sqrt 7 } \right)}^2} + 2.\sqrt 7 .2 + {2^2}} \\ \Leftrightarrow B = 3 - \sqrt 7 + \sqrt {{{\left( {\sqrt 7 + 2} \right)}^2}} \,\,\left( {Do\,\,3 - \sqrt 7 > 0} \right)\\ \Leftrightarrow B = 3 - \sqrt 7 + \left| {\sqrt 7 + 2} \right|\\ \Leftrightarrow B = 3 - \sqrt 7 + \sqrt 7 + 2\,\,\,\left( {Do\,\,\sqrt 7 + 2 > 0} \right)\\ \Leftrightarrow B = 5\end{array}\) Vậy \(B = 5\). Bài 2. (2,0 điểm) Cách giải: Giải các phương trình và hệ phương trình sau: a) \(3{x^2} - 7x + 4 = 0\). Nhận xét: Ta có: \(a + b + c = 3 + \left( { - 7} \right) + 4 = 0\) nên phương trình đã cho có 2 nghiệm phân biệt \({x_1} = 1\), \({x_2} = \dfrac{c}{a} = \dfrac{4}{3}\). Vậy tập nghiệm của phương trình là \(S = \left\{ {1;\dfrac{4}{3}} \right\}\). b) \(3{x^2} - 12 = 0\) \(\begin{array}{l} \Leftrightarrow 3{x^2} = 12\\ \Leftrightarrow {x^2} = 4\\ \Leftrightarrow x = \pm 2\end{array}\) Vậy tập nghiệm của phương trình là \(S = \left\{ { \pm 2} \right\}\). c) \(\left\{ \begin{array}{l}x + 3y = 8\\6x - 3y = 27\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}7x = 35\\x + 3y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\5 + 3y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\3y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 1\end{array} \right.\) Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {5;1} \right)\). d) \({x^4} - 4{x^2} + 4 = 0\) Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), khi đó phương trình trở thành: \({t^2} - 4t + 4 = 0\)\( \Leftrightarrow {\left( {t - 2} \right)^2} = 0 \Leftrightarrow t = 2\,\,\,\left( {tm} \right)\) Với \(t = 2 \Rightarrow {x^2} = 2 \Leftrightarrow x = \pm \sqrt 2 \). Vậy tập nghiệm của phương trình là \(S = \left\{ { \pm \sqrt 2 } \right\}\). Bài 3. (2 điểm) Cách giải: a) Trong mặt phẳng tọa độ \(Oxy,\) cho hàm số \(y = \dfrac{1}{2}{x^2}\) có đồ thị \(\left( P \right).\) Vẽ đồ thị \(\left( P \right).\) Ta có bảng giá trị:
Vậy đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) là đường cong nhận trục tung làm trục đối xứng và đi qua các điểm \(\left( { - 4;\,\,8} \right),\,\,\left( { - 2;\,\,2} \right),\,\,\left( {0;\,\,0} \right),\,\,\,\left( {2;\,\,2} \right),\,\,\,\left( {4;\,\,8} \right).\) Đồ thị hàm số:
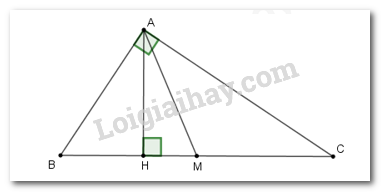
b) Cho phương trình \({x^2} + \left( {2m - 5} \right)x + 4 - 2m = 0\) (\(x\) là ẩn số, \(m\) là tham số). Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^3 + x_2^3 = 1.\) Xét phương trình \({x^2} + \left( {2m - 5} \right)x + 4 - 2m = 0\,\,\,\,\left( * \right)\). Phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \( \Leftrightarrow \Delta > 0\) \(\begin{array}{l} \Leftrightarrow {\left( {2m - 5} \right)^2} - 4.\left( {4 - 2m} \right) > 0\\ \Leftrightarrow 4{m^2} - 20m + 25 - 16 + 8m > 0\\ \Leftrightarrow 4{m^2} - 12m + 9 > 0\\ \Leftrightarrow {\left( {2m - 3} \right)^2} > 0\\ \Leftrightarrow 2m - 3 \ne 0 \Leftrightarrow m \ne \dfrac{3}{2}\end{array}\) Với \(m \ne \dfrac{3}{2}\) thì phương trình \(\left( * \right)\) có hai nghiệm phân biệt\({x_1},\,\,{x_2}.\) Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2m + 5\\{x_1}{x_2} = 4 - 2m\end{array} \right..\) Theo đề bài ta có: \(x_1^3 + x_2^3 = 1\) \(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 1\\ \Leftrightarrow {\left( { - 2m + 5} \right)^3} - 3\left( {4 - 2m} \right)\left( { - 2m + 5} \right) = 1\\ \Leftrightarrow - 8{m^3} + 60{m^2} - 150m + 125 - 60 - 12{m^2} + 54m = 1\\ \Leftrightarrow - 8{m^3} + 48{m^2} - 96m + 64 = 0\\ \Leftrightarrow {\left( { - 2m + 4} \right)^3} = 0\\ \Leftrightarrow - 2m + 4 = 0\\ \Leftrightarrow 2m = 4\\ \Leftrightarrow m = 2\,\,\left( {tm} \right)\end{array}\) Vậy \(m = 2\). Bài 4. (1,0 điểm) Cách giải: Một người dự định đi xe máy từ Vĩnh Long đến Sóc Trăng cách nhau 90 km. Vì có việc gấp cần đến Sóc Trăng trước giờ dự định 27 phút, nên người ấy phải tăng vận tốc thêm 10 km/h. Hãy tính vận tốc xe máy mà người đó dự định đi. Gọi vận tốc dự định của người đó là \(x\,\,\left( {km/h} \right),\,\,\,\left( {x > 0} \right).\) \( \Rightarrow \) Thời gian dự định người đó đi đến Sóc Trăng là: \(\dfrac{{90}}{x}\,\,\left( h \right).\) Vận tốc thực tế người đó đi là: \(x + 10\,\,\left( {km/h} \right).\) \( \Rightarrow \) Thời gian thực tế người đó đi đến Sóc Trăng là:\(\dfrac{{90}}{{x + 10}}\,\,\left( h \right).\) Người đó đến Sóc Trăng sớm hơn dự định \(27\) phút \( = \dfrac{{27}}{{60}} = \dfrac{9}{{20}}\) giờ nên ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\dfrac{{90}}{x} - \dfrac{{90}}{{x + 10}} = \dfrac{9}{{20}} \Leftrightarrow \dfrac{{10}}{x} - \dfrac{{10}}{{x + 10}} = \dfrac{1}{{20}}\\ \Leftrightarrow 10.20\left( {x + 10} \right) - 10.20x = x\left( {x + 10} \right)\\ \Leftrightarrow 2000 = {x^2} + 10x\\ \Leftrightarrow {x^2} + 10x - 2000 = 0\\ \Leftrightarrow {x^2} + 50x - 40x - 2000 = 0\\ \Leftrightarrow x\left( {x + 50} \right) - 40\left( {x + 50} \right) = 0\\ \Leftrightarrow \left( {x + 50} \right)\left( {x - 40} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 50 = 0\\x - 40 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 50\,\,\,\left( {ktm} \right)\\x = 40\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy vận tốc dự định của người đó là 40 km/h. Bài 5. (1,0 điểm) Cách giải: Cho tam giác \(ABC\) vuông tại \(A\) , đường cao AH. Biết \(BH = 4cm,{\rm{ }}CH = 9cm\)
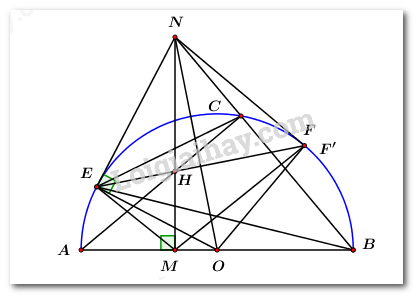
a) Tính độ dài đường cao AH và số đo \(\angle ABH\) (làm tròn đến độ) Xét tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH,\) theo hệ thức lượng trong tam giác vuông ta có: \(A{H^2} = BH.CH = 4.9 = 36\) \( \Rightarrow AH = 6cm\). Xét tam giác \(ABH\) vuông tại \(H\) ta có: \(\tan \angle ABH = \dfrac{{AH}}{{BH}} = \dfrac{6}{4} = 1,5\) \( \Rightarrow \angle ABH \approx {56^0}\) . Vậy \(AH = 6\,\,cm\) và \(\angle ABH \approx {56^0}\). b) Vẽ đường trung tuyến AM của tam giác ABC \(\left( {M \in BC} \right)\) , tính diện tích tam giác \(AHM.\) Ta có: \(BC = BH + CH = 4 + 9 = 13\,\,\left( {cm} \right)\). Vì \(M\) là trung điểm cạnh \(BC\) nên \(BM = \dfrac{{BC}}{2} = \dfrac{{13}}{2} = 6,5\,\,\left( {cm} \right)\). Suy ra \(HM = BM - BH = 6,5 - 4 = 2,5\,\,\left( {cm} \right)\). Diện tích tam giác \(AHM\) vuông tại \(H\) là \({S_{AHM}} = \dfrac{1}{2}AH.HM = \dfrac{1}{2}.6.2,5 = 7,5\,\,\,\left( {c{m^2}} \right)\). Bài 6. (2,5 điểm) Cách giải: Cho nửa đường tròn tâm O đường kính AB. Vẽ đường thẳng \(d\) vuông góc với OA tại M \(\left( {M \ne O,A} \right)\). Trên \(d\) lấy điểm N sao cho N nằm bên ngoài nửa đường tròn \(\left( O \right)\). Kẻ tiếp tuyến \(NE\) với nửa đường tròn \(\left( O \right)\) (E là tiếp điểm, E và A nằm cùng phía đối với đường thẳng \(d\))
a) Chứng minh tứ giác OMEN nội tiếp được đường tròn. Ta có: \(d \bot OA \Rightarrow \angle NMO = {90^0}\) \(NE\) là tiếp tuyến với \(\left( O \right)\) tại \(E\) nên \(OE \bot NE \Rightarrow \angle NEO = {90^0}\) Tứ giác \(OMEN\) có \(\angle NMO = \angle NEO = {90^0}\) Nên \(OMEN\) là tứ giác nội tiếp (hai đỉnh kề một cạnh cùng nhìn cạnh đối diện dưới các góc bằng) (đpcm) b) Nối NB cắt nửa đường tròn (O) tại C. Chứng minh \(N{E^2} = NC.NB\). Nối \(E\) với \(C,\,\,E\) với \(B.\) Xét \(\Delta NEC\) và \(\Delta NBE\) có: \(\angle N\,\,\,chung\) \(\angle NBE = \angle NEC\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(EC\)) \( \Rightarrow \Delta NEC \sim \Delta NBE\left( {g - g} \right)\) \( \Rightarrow \dfrac{{NE}}{{NB}} = \dfrac{{NC}}{{NE}}\) (các cặp cạnh tương ứng tỉ lệ) \( \Rightarrow N{E^2} = NB.NC\) (đpcm) c) Gọi H là giao điểm của AC và \(d\), F là giao điểm của tia EH và nửa đường tròn (O). Chứng minh \(\angle NEF = \angle NOF\) Xét \(\Delta NCH\) và \(\Delta NMB\) có: \(\begin{array}{l}\angle N\,\,\,chung\\\angle NCH = \angle NMB = {90^0}\\ \Rightarrow \Delta NCH \sim \Delta NMB\,\,\,\left( {g - g} \right)\end{array}\) \( \Rightarrow \dfrac{{NC}}{{NM}} = \dfrac{{NH}}{{NB}}\) (các cặp cạnh tương ứng tỉ lệ) \( \Rightarrow NC.NB = NH.NM\) Mà \(N{E^2} = NB.NC\,\,\,\,\left( {cmt} \right)\) nên \(N{E^2} = NH.NM\) \( \Rightarrow \dfrac{{NE}}{{NM}} = \dfrac{{NH}}{{NE}}\) Xét \(\Delta NEH\) và \(\Delta NME\) có: \(\begin{array}{l}\angle N\,\,\,chung\\\dfrac{{NE}}{{NM}} = \dfrac{{NH}}{{NE}}\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta NEH \sim \Delta NME\,\,\,\,\left( {c - g - c} \right)\end{array}\) \( \Rightarrow \angle NHE = \angle NEM\) (các góc tương ứng) (1) Kẻ tiếp tuyến \(NF'\) với nửa đường tròn \(\left( O \right).\) Do \(NE = NF'\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow NF{'^2} = NH.NM\) \( \Rightarrow \dfrac{{NF'}}{{NH}} = \dfrac{{NM}}{{NF'}}\) Xét \(\Delta NF'H\) và \(\Delta NMF'\) có: \(\begin{array}{l}\angle N\,\,\,chung\\\dfrac{{NF'}}{{NH}} = \dfrac{{NM}}{{NF'}}\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta NF'H \sim \Delta NMF'\,\,\,\left( {c - g - c} \right)\end{array}\) \( \Rightarrow \angle NHF' = \angle NF'M\) (các góc tương ứng) (2) Lại có tứ giác \(OMEN\) nội tiếp (câu a) nên bốn điểm \(O,\,\,M,\,\,E,\,\,N\) cùng thuộc một đường tròn. (3) Tứ giác \(OENF'\) có \(\angle OEN + \angle OF'N = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)) Do đó bốn điểm \(O,\,\,E,\,\,N,\,\,F'\) cùng thuộc một đường tròn. (4) Từ (3) và (4) suy ra 5 điểm \(O,\,\,M,\,\,E,\,\,N,\,\,F'\) cùng thuộc một đường tròn. \( \Rightarrow \) Tứ giác \(MENF'\) nội tiếp. \( \Rightarrow \angle NEM + \angle NF'M = {180^0}\) (tính chất) (5) Từ (1), (2) và (5) suy ra \( \Rightarrow \angle NHE + \angle NHF' = \angle NEM + \angle NF'M = {180^0}\) \( \Rightarrow E,H,F'\) thằng hàng hay \(F'\) là giao điểm của \(EH\) với nửa đường tròn \(\left( O \right)\) \( \Rightarrow F' \equiv F\) \( \Rightarrow \) Tứ giác \(NEOF\) nội tiếp \( \Rightarrow \angle NEF = \angle NOF\) (hai góc nội tiếp cùng chắn cung \(NF\)) (đpcm). Bài 7. (0,5 điểm) Cách giải: Cho hai phương trình \({x^2} + \left( {2{m^2} + 1} \right)x + {m^3} + 7\sqrt 2 - 23 = 0\,\,\,\left( 1 \right)\) và \(2{x^2} + \left( {{m^2} - m} \right)x + 9\sqrt 2 - 30 = 0\,\,\,\left( 2 \right)\) (\(x\) là ẩn số, \(m\) là tham số). Tìm giá trị của tham số \(m\) để phương trình (1) và phương trình (2) có nghiệm chung \(x = 3\). Phương trình (1) có hai nghiệm \({\Delta _1} \ge 0\) \(\begin{array}{l} \Leftrightarrow {\left( {2{m^2} + 1} \right)^2} - 4\left( {{m^3} + 7\sqrt 2 - 23} \right) \ge 0\\ \Leftrightarrow 4{m^4} + 4{m^2} + 1 - 4{m^3} - 28\sqrt 2 + 92 \ge 0\\ \Leftrightarrow 4{m^4} - 4{m^3} + 4{m^2} - 28\sqrt 2 + 93 \ge 0\,\,\,\,\,\left( * \right)\end{array}\) Phương trình (2) có hai nghiệm \({\Delta _2} \ge 0\) \(\begin{array}{l} \Leftrightarrow {\left( {{m^2} - m} \right)^2} - 8\left( {9\sqrt 2 - 30} \right) \ge 0\\ \Leftrightarrow {m^4} - 2{m^3} + {m^2} - 72\sqrt 2 + 240 \ge 0\,\,\,\left( {**} \right)\end{array}\) Hai phương trình đã cho có nghiệm chung là \(x = 3\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}9 + \left( {2{m^2} + 1} \right).3 + {m^3} + 7\sqrt 2 - 23 = 0\\2.9 + \left( {{m^2} - m} \right).3 + 9\sqrt 2 - 30 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^3} + 6{m^2} + 7\sqrt 2 - 11 = 0\\3{m^2} - 3m + 9\sqrt 2 - 12 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^3} + 6{m^2} + 7\sqrt 2 - 11 = 0\,\,\,\,\left( 3 \right)\\{m^2} - m + 3\sqrt 2 - 4 = 0\,\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)\end{array} \right.\end{array}\) Giải phương trình (4) ta được: \(\begin{array}{l}\left( 4 \right) \Leftrightarrow {m^2} - m = 4 - 3\sqrt 2 \\ \Leftrightarrow {m^2} - 2.m.\dfrac{1}{2} + \dfrac{1}{4} = \dfrac{{17}}{4} - 3\sqrt 2 \\ \Leftrightarrow {\left( {m - \dfrac{1}{2}} \right)^2} = \dfrac{{17 - 12\sqrt 2 }}{4}\\ \Leftrightarrow {\left( {m - \dfrac{1}{2}} \right)^2} = \dfrac{{9 - 2.3.2\sqrt 2 + 8}}{4}\\ \Leftrightarrow {\left( {m - \dfrac{1}{2}} \right)^2} = \dfrac{{{{\left( {3 - 2\sqrt 2 } \right)}^2}}}{4}\\ \Leftrightarrow \left[ \begin{array}{l}m - \dfrac{1}{2} = \dfrac{{3 - 2\sqrt 2 }}{2}\\m - \dfrac{1}{2} = - \dfrac{{3 - 2\sqrt 2 }}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = 2 - \sqrt 2 \,\,\,\,\left( {tm\,\,\,\left( * \right),\,\,\left( {**} \right)} \right)\\m = \sqrt 2 - 1\,\,\,\left( {tm\,\,\,\left( * \right),\,\,\left( {**} \right)} \right)\end{array} \right.\end{array}\) +) Với \(m = 2 - \sqrt 2 \) ta có: \(\begin{array}{l}\left( 3 \right) \Leftrightarrow {\left( {2 - \sqrt 2 } \right)^3} + 6{\left( {2 - \sqrt 2 } \right)^2} + 7\sqrt 2 - 11 = 0\\ \Leftrightarrow 20 - 14\sqrt 2 + 6\left( {6 - 4\sqrt 2 } \right) + 7\sqrt 2 - 11 = 0\\ \Leftrightarrow 9 - 7\sqrt 2 + 36 - 24\sqrt 2 = 0\\ \Leftrightarrow 45 - 31\sqrt 2 = 0\,\,\,\left( {ktm} \right)\end{array}\) \( \Rightarrow m = 2 - \sqrt 2 \) không thỏa mãn bài toán. +) Với \(m = \sqrt 2 - 1\) ta có: \(\begin{array}{l}\left( 3 \right) \Leftrightarrow {\left( {\sqrt 2 - 1} \right)^3} + 6{\left( {\sqrt 2 - 1} \right)^2} + 7\sqrt 2 - 11 = 0\\ \Leftrightarrow - 7 + 5\sqrt 2 + 6\left( {3 - 2\sqrt 2 } \right) + 7\sqrt 2 - 11 = 0\\ \Leftrightarrow - 18 + 12\sqrt 2 + 18 - 12\sqrt 2 = 0\\ \Leftrightarrow 0 = 0\,\,\,\left( {tm} \right)\end{array}\) \( \Rightarrow m = \sqrt 2 - 1\) thỏa mãn bài toán. Vậy \(m = \sqrt 2 - 1\) thỏa mãn bài toán.
|




















Danh sách bình luận