Đề thi vào 10 môn Toán Vĩnh Long năm 2019

Đề bài

Bài 1 (1,0 điểm)

Tính giá trị biểu thức:

a) \(A = 2\sqrt {48}  + 3\sqrt {75}  - 2\sqrt {108} \)

b) \(B = \sqrt {19 + 8\sqrt 3 }  + \sqrt {19 - 8\sqrt 3 } \)

Bài 2 (2,0 điểm): Giải các phương trình và hệ phương trình sau:

a) \(2{x^2} - 3x - 2 = 0\)                                 b) \(5{x^2} + 2x = 0\)

c) \({x^4} - 4{x^2} - 5 = 0\)                           d) \(\left\{ \begin{array}{l}2x - y =  - 7\\3x + y = 27\end{array} \right.\) 

Bài 3 (2 điểm): Trong mặt phẳng tọa độ \(Oxy,\) cho hàm số \(y =  - {x^2}\)  có đồ thị \(\left( P \right).\)

a) Vẽ đồ thị \(\left( P \right)\)

b) Tìm giá trị của \(m\) để đường thẳng \(\left( d \right):y = 2x - 3m\) (với \(m\)là tham số) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ là \({x_1},{x_2}\) thỏa mãn \({x_1}x_2^2 + {x_2}\left( {3m - 2{x_1}} \right) = 6\)

Câu 4 (1,0 điểm) Một công ty vận tải dự định dùng loại xe lớn để vận chuyển 20 tấn hàng hóa theo một hợp đồng. Nhưng khi vào việc công ty không còn xe lớn nên phải thay bằng những xe nhỏ. Mỗi xe nhỏ vận chuyển được khối lượng ít hơn 1 tấn so với mỗi xe lớn theo dự định. Để đảm bảo thời gian đã hợp đồng, công ty phải dùng một số lượng xe nhiều hơn số xe dự định là 1 xe. Hỏi mỗi xe nhỏ vận chuyển bao nhiêu tấn hàng hóa (Biết các xe cùng loại thì có khối lượng vận chuyển như nhau).

Bài 5 (1 điểm): Cho tam giác \(ABC\) có \(AB = 4cm,\,\,\,AC = 4\sqrt 3 ,\,\,BC = 8cm.\)

a) Chứng minh tam giác \(ABC\) vuông.

b) Tính số đo \(\angle B,\,\,\angle C\) và độ dài đường cao \(AH\) của \(\Delta ABC.\)

Bài 6 (2,5 điểm)

Cho đường tròn \(\left( O \right)\) đường kính \(AB\) và điểm \(M\) bất kì thuộc đường tròn sao cho  \(\left( {M \ne A} \right)\). Kẻ tiếp tuyến tại \(A\) của đường tròn, tiếp tuyến này cắt tia \(BM\) ở \(N\). Tiếp tuyến của đường tròn tại \(M\) cắt \(AN\) ở \(D\).

a) Chứng minh bốn điểm \(A,\,\,D,\,\,M,\,\,O\) cùng thuộc một đường tròn.

b) Chứng minh \(OD\) song song với \(BM\).

c) Qua \(O\) kẻ đường thẳng vuông góc với \(AB\) và cắt đường thẳng \(BM\) tại \(I\). Gọi giao điểm của \(AI\) và \(BD\) là \(G\). Chứng minh \(N,\,\,G,\,\,O\) thẳng hàng.

Bài 7 (0,5 điểm)

Cho \(x,\,\,y\) là các số thực dương thỏa mãn \(x + y = 1.\)

Tìm giá trị nhỏ nhất của biểu thức \(A = 2{x^2} - {y^2} + x + \dfrac{1}{x} + 1.\)

Lời giải

Bài 1 (TH):

Phương pháp:

a) Sử dụng công thức \(\sqrt {{A^2}B}  = \left| A \right|\sqrt B \,\,\,\left( {B \ge 0} \right)\).

b) Đưa các biểu thức dưới dấu căn về hằng đẳng thức.

Cách giải:

a) \(A = 2\sqrt {48}  + 3\sqrt {75}  - 2\sqrt {108} \)

\(\begin{array}{l}A = 2\sqrt {{4^2}.3}  + 3\sqrt {{5^2}.3}  - 2\sqrt {{6^2}.3} \\A = 2.4.\sqrt 3  + 3.5\sqrt 3  - 2.6\sqrt 3 \\A = 8\sqrt 3  + 15\sqrt 3  - 12\sqrt 3 \\A = \left( {8 + 15 - 12} \right)\sqrt 3  = 11\sqrt 3 \end{array}\)

Vậy \(A = 11\sqrt 3 \).

b) \(B = \sqrt {19 + 8\sqrt 3 }  + \sqrt {19 - 8\sqrt 3 } \)

\(\begin{array}{l}B = \sqrt {{4^2} + 2.4.\sqrt 3  + {{\left( {\sqrt 3 } \right)}^2}}  + \sqrt {{4^2} - 2.4.\sqrt 3  + {{\left( {\sqrt 3 } \right)}^2}} \\B = \sqrt {{{\left( {4 + \sqrt 3 } \right)}^2}}  + \sqrt {{{\left( {4 - \sqrt 3 } \right)}^2}} \\B = \left| {4 + \sqrt 3 } \right| + \left| {4 - \sqrt 3 } \right|\\B = 4 + \sqrt 3  + 4 - \sqrt 3 \,\,\left( {Do\,\,4 + \sqrt 3  > 0;\,\,4 - \sqrt 3  > 0} \right)\\B = 8\end{array}\)

Vậy \(B = 8\).

Bài 2 (TH):

Phương pháp:

a, b) Đưa phương trình về dạng tích rồi giải phương trình tích, hoặc dùng công thức nghiệm cho phương trình bậc hai.

c) Đặt \(t = {x^2}\), đặt điều kiện và giải phương trình ẩn \(t\). Đối chiếu điều kiện rồi tìm \(x\).

d) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.

Cách giải:

a) \(2{x^2} - 3x - 2 = 0\) \( \Leftrightarrow 2{x^2} - 4x + x - 2 = 0 \Leftrightarrow 2x\left( {x - 2} \right) + \left( {x - 2} \right) = 0\)

\( \Leftrightarrow \left( {2x + 1} \right)\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{1}{2}\\x = 2\end{array} \right.\)

Vậy phương trình có tập nghiệm \(S = \left\{ { - \dfrac{1}{2};2} \right\}\).

b) \(5{x^2} + 2x = 0 \Leftrightarrow x\left( {5x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\5x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - \dfrac{2}{5}\end{array} \right.\)

Vậy phương trình có tập nghiệm \(S = \left\{ {0; - \dfrac{2}{5}} \right\}\).

c) Đặt \(t = {x^2}\left( {t \ge 0} \right)\).

Khi đó phương trình trở thành \({t^2} - 4t - 5 = 0 \Leftrightarrow \left( {t + 1} \right)\left( {t - 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t =  - 1\,\,\,\left( {ktm} \right)\\t = 5\,\,\,\,\,\left( {tm} \right)\end{array} \right.\)

Với \(t = 5 \Leftrightarrow {x^2} = 5 \Leftrightarrow x =  \pm \sqrt 5 \).

Vậy phương trình đã cho có tập nghiệm \(S = \left\{ { - \sqrt 5 ;\sqrt 5 } \right\}\).

d) \(\left\{ \begin{array}{l}2x - y =  - 7\\3x + y = 27\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 20\\2x - y =  - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\2.4 - y =  - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 15\end{array} \right.\)

Vậy hệ đã cho có nghiệm \(\left( {x;y} \right)\) là \(\left( {4;15} \right)\).

Bài 3 (VD)

Phương pháp:

a) Lập bảng giá trị rồi vẽ đồ thị hàm số

b) Xét phương trình hoành độ giao điểm rồi tìm điều kiện đề phương trình có hai nghiệm phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\end{array} \right.\)

Biến đổi giả thiết để xuất hiện tích hai nghiệm rồi sử dụng hệ thức Vi-et

Cách giải:

a) Vẽ đồ thị \(\left( P \right)\)

Bảng giá trị của hàm số \(y =  - {x^2}.\)

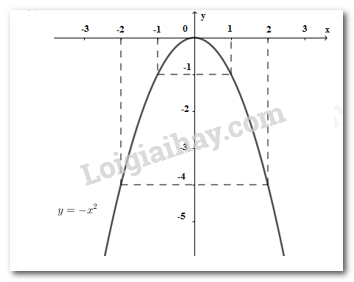
Vẽ đường cong đi qua các điểm có tọa độ \(\left( { - 2; - 4} \right),\left( { - 1; - 1} \right),\left( {0;0} \right),\left( {1; - 1} \right);,\left( {2; - 4} \right)\) ta được parabol \(\left( P \right):y =  - {x^2}.\)

Hình vẽ:

b) Tìm giá trị của \(m\) để đường thẳng \(\left( d \right):y = 2x - 3m\) (với \(m\)là tham số) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ là \({x_1},{x_2}\) thỏa mãn \({x_1}x_2^2 + {x_2}\left( {3m - 2{x_1}} \right) = 6\)

Xét phương trình hoành độ giao điểm của đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\), ta có

\( - {x^2} = 2x - 3m \Leftrightarrow {x^2} + 2x - 3m = 0\) (*)

Phương trình (*) có \(\Delta ' = {1^2} - 1.\left( { - 3m} \right) = 1 + 3m\)

Để đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ là \({x_1},{x_2}\) thì phương trình (*) có hai nghiệm phân biệt \({x_1},{x_2}\) \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\,\,\left( {luon\,\,dung} \right)\\1 + 3m > 0\end{array} \right. \Leftrightarrow m >  - \dfrac{1}{3}.\)

Theo hệ thức Vi-ét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 2\\{x_1}{x_2} =  - 3m\end{array} \right.\)

Theo bài ra ta có

\({x_1}x_2^2 + {x_2}\left( {3m - 2{x_1}} \right) = 6\)

\(\begin{array}{l} \Leftrightarrow \left( {{x_1}{x_2}} \right).{x_2} + 3m{x_2} - 2{x_1}{x_2} = 6\\ \Leftrightarrow  - 3m{x_2} + 3m{x_2} - 2.\left( { - 3m} \right) = 6\\ \Leftrightarrow 6m = 6\\ \Leftrightarrow m = 1\left( {tm} \right)\end{array}\)

Vậy \(m = 1\) là giá trị cần tìm.

Bài 4 (VD): 

Phương pháp:

Bước 1: Lập phương trình

- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình.

Bước 3: Kết luận

Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

Cách giải:

Gọi số tấn hàng hóa mỗi xe nhỏ vận chuyển được là: \(x\) (tấn) \(\left( {x > 0} \right)\)

 Mỗi xe lớn vận chuyển được số tấn hàng là: \(x + 1\) (tấn)

Khi đó số xe nhỏ dự định phải dùng để chở hết 20 tấn hàng hóa là: \(\dfrac{{20}}{x}\) (xe) .

Số xe lớn dự định phải dùng  để chở hết 20 tấn hàng hóa là: \(\dfrac{{20}}{{x + 1}}\) (xe)

Vì thực tế số xe nhỏ phải dùng nhiều hơn dự định là 1 xe. Nên ta có phương trình: \(\dfrac{{20}}{x} - \dfrac{{20}}{{x + 1}} = 1\) 

Giải phương trình:

\(\begin{array}{l}\dfrac{{20}}{x} - \dfrac{{20}}{{x + 1}} = 1\,\, \Leftrightarrow 20.\left( {\dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right) = 1\\ \Leftrightarrow \dfrac{1}{x} - \dfrac{1}{{x + 1}} = \dfrac{1}{{20}} \Leftrightarrow \dfrac{{x + 1 - x}}{{x\left( {x + 1} \right)}} = \dfrac{1}{{20}}\\ \Leftrightarrow \dfrac{1}{{x\left( {x + 1} \right)}} = \dfrac{1}{{20}} \Leftrightarrow x\left( {x + 1} \right) = 20\\ \Leftrightarrow {x^2} + x - 20 = 0 \Leftrightarrow \left( {x + 5} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 5 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 5\left( {ktm} \right)\\x = 4\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

 Vậy mỗi xe nhỏ vận chuyển được  4 tấn hàng hóa.

Bài 5 (VD)

Phương pháp:

a) Áp dụng định lý Pitago đảo để chứng minh tam giác \(ABC\) vuông.

b) Sử dụng tỉ số lượng giác của góc nhọn và hệ thức lượng trong tam giác vuông để làm bài toán.

Cách giải:

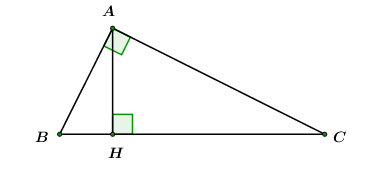
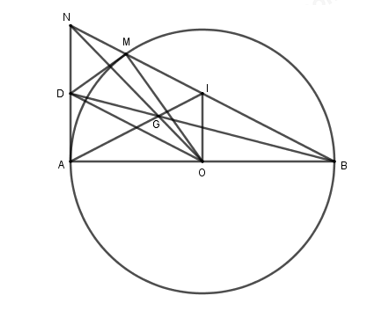
a) Chứng minh tam giác \(ABC\) vuông.

Ta có: \(A{B^2} = {4^2} = 16;\,\,A{C^2} = {\left( {4\sqrt 3 } \right)^2} = 48;\,\,B{C^2} = {8^2} = 64.\)

\( \Rightarrow A{B^2} + A{C^2} = 16 + 48 = 64 = B{C^2}\)

\( \Rightarrow \Delta ABC\) vuông tại \(A\) (định lý Pitago đảo).

b) Tính số đo \(\angle B,\,\,\angle C\) và độ dài đường cao \(AH\) của \(\Delta ABC.\)

Áp dụng tỉ số lượng giác của góc nhọn trong \(\Delta ABC\) ta có:

\(\begin{array}{l}\cos \angle B = \dfrac{{AB}}{{BC}} = \dfrac{4}{8} = \dfrac{1}{2} \Rightarrow \angle B = {60^0}\\ \Rightarrow \angle C = {180^0} - \angle B - \angle A = {180^0} - {60^0} - {90^0} = {30^0}.\end{array}\)

Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại\(A\) và có đường cao \(AH\) ta có:

\(AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{4.4\sqrt 3 }}{8} = 2\sqrt 3 \,\,cm.\)

Vậy \(\angle B = {60^0},\,\,\,\angle C = {30^0},\,\,\,AH = 2\sqrt 3 \,\,cm.\)

Bài 6 (2,5 điểm) (VD):

Phương pháp:

a) Chứng minh tổng hai góc đối của tứ giác bằng \({180^0}\).

b) Chứng minh hai góc ở vị trí đồng vị bằng nhau.

c) Chứng minh \(G\) là trọng tâm tam giác \(ABN\).

Cách giải:

a) Ta có: \(OM \bot MD\) (tính chất tiếp tuyến) \( \Rightarrow \angle OMD = {90^0}\)

\(OA \bot AD\) (tính chất tiếp tuyến) \( \Rightarrow \angle OAD = {90^0}\)

Tứ giác \(OMDA\) có \(\angle OMD + \angle OAD = {90^0} + {90^0} = {180^0}\), mà hai góc này ở vị trí đối diện nên tứ giác \(OMDA\) nội tiếp hay bốn điểm \(A,D,M,O\) cùng thuộc một đường tròn.

b) Xét (O) Ta có: \(OD\) là tia phân giác trong góc \(\angle MOA\) (tính chất hai tiếp tuyến cắt nhau)

\( \Rightarrow \angle MOD = \angle AOD = \dfrac{1}{2}\angle AOM\) (1)

Mà \(\angle MBA = \dfrac{1}{2}\angle MOA\) (góc nội tiếp và góc ở tâm cùng chắn cung \(MA\)) (2)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\angle AOD = \angle ABM\left( { = \dfrac{1}{2}\angle MOA} \right)\)

Mà hai góc này ở vị trí đồng vị nên \(OD//BM\) (đpcm).

c) Vì \(OI \bot AB,AN \bot AB \Rightarrow OI//AN\)

Mà \(O\) là trung điểm của \(AB\) \( \Rightarrow OI\) là đường trung bình của tam giác \(ABN\)

\( \Rightarrow I\) là trung điểm của \(BN\) \( \Rightarrow \)\(AI\) là trung tuyến của tam giác \(ABN\).

Lại có \(OD//BM\left( {cmt} \right)\), mà \(O\) là trung điểm của \(AB\)\( \Rightarrow OD\) là đường trung bình của tam giác \(ABN\)

\( \Rightarrow D\) là trung điểm của \(AN\) \( \Rightarrow \)\(BD\) là trung tuyến của tam giác \(ABN\).

Mà \(NO\) là trung tuyến của tam giác \(ABN\).

Mặt khác ta lại có: \(AI \cap BD = \left\{ G \right\}\)

Do đó \(AI,BD,NO\) đồng qui tại \(G\) là trọng tâm của tam giác \(ABN\).

Suy ra \(N,G,O\) thẳng hàng.

Bài 7 (VDC):

Phương pháp:

Thay \(y = 1 - x\) vào biểu thức và rút gọn.

Đánh giá GTNN của biểu thức thu được và kết luận.

Cách giải:

Ta có: \(x + y = 1 \Rightarrow y = 1 - x\) thay vào \(A\) ta được:

\(\begin{array}{l}A = 2{x^2} - {y^2} + x + \dfrac{1}{x} + 1 = 2{x^2} - {\left( {1 - x} \right)^2} + x + \dfrac{1}{x} + 1\\ = 2{x^2} - \left( {{x^2} - 2x + 1} \right) + x + \dfrac{1}{x} + 1 = {x^2} + 2x + x + \dfrac{1}{x}\\ = \left( {{x^2} - x + \dfrac{1}{4}} \right) + \left( {4x + \dfrac{1}{x}} \right) - \dfrac{1}{4} = {\left( {x - \dfrac{1}{2}} \right)^2} + \left( {4x + \dfrac{1}{x}} \right) - \dfrac{1}{4}.\end{array}\)

 Dễ thấy \({\left( {x - \dfrac{1}{2}} \right)^2} \ge 0,\forall x\).

Áp dụng bất đẳng thức Cô – si ta có \(4x + \dfrac{1}{x} \ge 2\sqrt {4x.\dfrac{1}{x}}  = 4\).

Suy ra \({\left( {x - \dfrac{1}{2}} \right)^2} + \left( {4x + \dfrac{1}{x}} \right) - \dfrac{1}{4} \ge 0 + 4 - \dfrac{1}{4} = \dfrac{{15}}{4}\).

Dấu “=” xảy ra khi \(x = \dfrac{1}{2}\).

Vậy \({A_{\min }} = \dfrac{{15}}{4}\) khi \(x = \dfrac{1}{2}\).