Đề thi vào 10 môn Toán Ninh Thuận năm 2023Tải vềCâu 1: Giải phương trình \(4x - 3 = 2 - x\) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
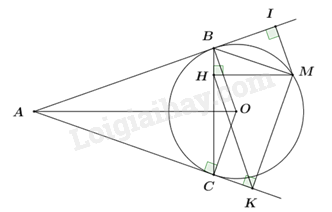
Đề bài Câu 1: Giải phương trình \(4x - 3 = 2 - x\) Câu 2: Cho biểu thức \(P = \frac{{\sqrt a {\rm{ \;}} + 3}}{{\sqrt a {\rm{ \;}} - 2}} + \frac{{1 - \sqrt a }}{{\sqrt a {\rm{ \;}} + 2}} + \frac{{4 - 4\sqrt a }}{{a - 4}}\) a) Với giá trị nào của a thì biểu thức P có nghĩa. b) Rút gọn biểu thức P. Câu 3: Cho Parabol \((P):y = {\rm{ \;}} - {x^2}\) và đường thẳng \((d):y = x - 2\). a) Vẽ \((P)\) và \((d)\) trên cùng một hệ trục tọa độ. b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép toán. Câu 4: Gia đình An dự định đi du lịch tại Nha Trang và Huế trong 7 ngày. Biết rằng chi phí trung bình mỗi ngày tại Nha Trang là 2 triệu đồng, còn tại Huế là 3 triệu đồng. Tính số ngày nghỉ dự định của gia đình An tại mỗi địa điểm, biết số tiền mà họ phải chi cho toàn bộ chuyến đi là 18 triệu đồng. Câu 5: Cho đường tròn (O) tâm O bán kính R và điểm A nằm ngoài đường tròn. Các tiếp tuyến với đường tròn kẻ từ A tiếp xúc với đường tròn tại B, C. Gọi M là điểm thuộc cung lớn BC. Từ M kẻ \(MH \bot BC,\) \(MK \bot AC,\) \(MI \bot AB\). a) Chứng minh tứ giác MIBH nội tiếp. b) Giả sử AB = 2R. Tính diện tích tứ giác ABOC. c) Chứng minh: \(MI.MK = M{H^2}\) Câu 6: Cho hai số thực dương a, b thỏa mãn điều kiện \(a + b = 2\). Tìm giá trị nhỏ nhất của biểu thức \(M = \left( {1 - \frac{4}{{{a^2}}}} \right)\left( {1 - \frac{4}{{{b^2}}}} \right)\)
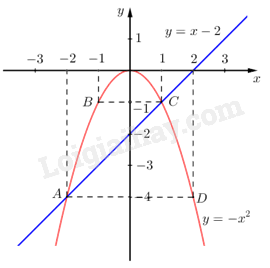
-----HẾT----- Lời giải chi tiết Câu 1 (NB): Phương pháp: Chuyển vế đổi dấu. Cách giải: Ta có: \(\begin{array}{*{20}{l}}{4x - 3 = 2 - x}\\{ \Leftrightarrow 4x + x = 2 + 3}\\{ \Leftrightarrow 5x = 5}\\{ \Leftrightarrow x = 1}\end{array}\) Vậy nghiệm của phương trình là \(x = 1\). Câu 2 (TH): Phương pháp: a) Điều kiện xác định của biểu thức: - Biểu thức trong căn có nghĩa: \(\sqrt {f(x)} \) có nghĩa \( \Leftrightarrow f(x) \ge 0\) - Mẫu thức khác 0. b) Rút gọn biểu thức (quy đồng, tính toán, đổi dấu) Cách giải: a) Biểu thức P có nghĩa khi \(\left\{ {\begin{array}{*{20}{l}}{a \ge 0}\\{\sqrt a {\rm{ \;}} - 2 \ne 0}\\{\sqrt a {\rm{ \;}} + 2 \ne 0}\\{a - 4 \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a \ge 0}\\{a \ne 4}\end{array}} \right.\) Vậy biểu thức P có nghĩa khi \(a \ge 0,{\mkern 1mu} {\mkern 1mu} a \ne 4\). b) Với \(a \ge 0,{\mkern 1mu} {\mkern 1mu} a \ne 4\) ta có: \(\begin{array}{l}\,\,\,\,\,\,P = \frac{{\sqrt a + 3}}{{\sqrt a - 2}} + \frac{{1 - \sqrt a }}{{\sqrt a + 2}} + \frac{{4 - 4\sqrt a }}{{a - 4}}\\ \Leftrightarrow P = \frac{{\left( {\sqrt a + 3} \right)\left( {\sqrt a + 2} \right)}}{{\left( {\sqrt a - 2} \right)\left( {\sqrt a + 2} \right)}} + \frac{{\left( {1 - \sqrt a } \right)\left( {\sqrt a - 2} \right)}}{{\left( {\sqrt a - 2} \right)\left( {\sqrt a + 2} \right)}} + \frac{{4 - 4\sqrt a }}{{\left( {\sqrt a - 2} \right)\left( {\sqrt a + 2} \right)}}\\ \Leftrightarrow P = \frac{{\left( {\sqrt a + 3} \right)\left( {\sqrt a + 2} \right) + \left( {1 - \sqrt a } \right)\left( {\sqrt a - 2} \right) + 4 - 4\sqrt a }}{{\left( {\sqrt a - 2} \right)\left( {\sqrt a + 2} \right)}}\\ \Leftrightarrow P = \frac{{a + 2\sqrt a + 3\sqrt a + 6 + \sqrt a - 2 - a + 2\sqrt a + 4 - 4\sqrt a }}{{\left( {\sqrt a - 2} \right)\left( {\sqrt a + 2} \right)}}\end{array}\) \(\begin{array}{*{20}{l}}{ \Leftrightarrow P = \frac{{4\sqrt a {\rm{ \;}} + 8}}{{\left( {\sqrt a {\rm{ \;}} - 2} \right)\left( {\sqrt a {\rm{ \;}} + 2} \right)}}}\\{ \Leftrightarrow P = \frac{{4\left( {\sqrt a {\rm{ \;}} + 2} \right)}}{{\left( {\sqrt a {\rm{ \;}} - 2} \right)\left( {\sqrt a {\rm{ \;}} + 2} \right)}}}\\{ \Leftrightarrow P = \frac{4}{{\sqrt a {\rm{ \;}} - 2}}}\end{array}\) Vậy với \(a \ge 0,{\mkern 1mu} {\mkern 1mu} a \ne 4\) thì \(P = \frac{4}{{\sqrt a {\rm{ \;}} - 2}}\). Câu 3 (TH): Phương pháp: a) Cách vẽ đồ thị hàm số \(y = a{x^2}(a \ne 0)\) Bước 1: Tìm tập xác định của hàm số. Bước 2: Lập bảng giá trị tương ứng giữa \(x\) và \(y\). Bước 3: Vẽ đồ thị và kết luận. * Chú ý: vì đồ thị hàm số y \( = a{x^2}(a \ne 0)\) luôn đi qua gốc tọa độ \(O\) và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này , ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy. Cách vẽ đồ thị hàm số \(y = ax + b(a \ne 0)\) Bước 1: Cho \(x = 0\) thì \(y = b\), ta được điểm \(P(0;b)\) thuộc trục Oy. Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( {\frac{{ - b}}{a};0} \right)\) thuộc trục hoành Ox. Bước 2: Vẽ đường thẳng đi qua hai điểm \({\rm{P}}\) và \({\rm{Q}}\) ta được đồ thị hàm số \(y = ax + b\) b) Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) Cách giải: a) * Vẽ đồ thị \((d):y = x - 2\) Với \(x = 0 \Rightarrow y = 0 - 2 = {\rm{ \;}} - 2\) Với \(y = 0 \Rightarrow x - 2 = 0 \Rightarrow x = 2\) Đồ thị hàm số \(y = x - 2\) là đường thẳng đi qua 2 điểm \(M\left( {0; - 2} \right)\) và \(N\left( {2;0} \right)\). * Vẽ đồ thị \((P):y = {\rm{ \;}} - {x^2}\) Ta có bảng giá trị sau:
\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm: \(O{\mkern 1mu} \left( {0;0} \right);A\left( { - 2; - 4} \right);{\mkern 1mu} {\mkern 1mu} B\left( { - 1; - 1} \right);C\left( {1; - 1} \right);{\mkern 1mu} {\mkern 1mu} D\left( {2; - 4} \right)\) Hệ số \(a = {\rm{ \;}} - 1 < 0\)nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng. Ta vẽ được đồ thị hàm số \(\left( d \right):{\mkern 1mu} {\mkern 1mu} y = x - 2\) và \((P):y = {\rm{ \;}} - {x^2}\) trên cùng hệ trục toạ độ như sau:
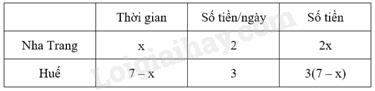
b) Xét phương trình hoành độ giao điểm của của \(\left( P \right)\) và \(\left( d \right)\) ta có: \(\begin{array}{*{20}{l}}{ - {x^2} = x - 2}\\{ \Leftrightarrow {x^2} + x - 2 = 0}\end{array}\) Ta có \(a + b + c = 1 + 1 + \left( { - 2} \right) = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = \frac{c}{a} = {\rm{ \;}} - 2}\end{array}} \right.\). Với \(x = 1 \Rightarrow y = {\rm{ \;}} - {1^2} = {\rm{ \;}} - 1\) Với \(x = {\rm{ \;}} - 2 \Rightarrow y = {\rm{ \;}} - {\left( { - 2} \right)^2} = {\rm{ \;}} - 4\). Vậy \(\left( P \right)\) cắt \(\left( d \right)\) tại hai điểm \(\left( {1; - 1} \right)\) và \(\left( { - 2; - 4} \right)\). Câu 4 (TH): Phương pháp: Giải bài toán bằng cách lập phương trình
Tổng số tiền đi cả hai nơi là 18 triệu đồng. Cách giải: Gọi số ngày gia đình An dự định đi du lịch tại Nha Trang là \(x\)(ngày) Điều kiện: \(x \in \mathbb{N}*;x < 7\). Số ngày gia đình An dự định đi du lịch tại Huế là 7 – x (ngày) Theo đề bài, chi phí trung bình mỗi ngày tại Nha Trang là 2 triệu đồng, còn tại Huế là 3 triệu đồng nên ta có phương trình: \(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 2x + 3(7 - x) = 18}\\{ \Leftrightarrow 2x + 21 - 3x = 18}\\{ \Leftrightarrow x = 3{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (tm)}\end{array}\) Số ngày gia đình An dự định đi du lịch tại Huế là: 7 – 3 = 4 (ngày) Vậy số ngày gia đình An dự định đi du lịch tại Nha Trang là 3 ngày; số ngày gia đình An dự định đi du lịch tại Huế là 4 ngày. Câu 5 (VD): Phương pháp: a) Chứng minh MIBH có hai tổng hai góc đối bằng \(180^\circ \) nên là tứ giác nội tiếp b) Sử dụng tính chất hai tiếp tuyến cắt nhau, ta chứng minh được \(\Delta OAB = \Delta OAC\) (cạnh huyền – cạnh góc vuông) Suy ra \({S_{ABOC}} = 2.{S_{OAB}}\) c) Chứng minh MKCH có hai tổng hai góc đối bằng \(180^\circ \) nên là tứ giác nội tiếp Sử dụng tính chất góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung thì bằng nhau. Từ đó $\Rightarrow \Delta MHI\backsim \Delta MKH\left( g.g \right)$, suy ra các cặp cạnh tương ứng tỉ lệ. Cách giải:
a) Ta có \(MI \bot AB{\mkern 1mu} {\mkern 1mu} \left( {gt} \right) \Rightarrow \angle MIB = {90^0}\) \(MH \bot BC{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {gt} \right) \Rightarrow \angle MHB = {90^0}\) Xét tứ giác MIBH có \(\angle MIB + \angle MHB = {90^0} + {90^0} = {180^0} \Rightarrow MIBH\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)) (đpcm). b) Tam giác AOB có \(AB \bot OB\) (giá trị) nên \(\Delta AOB\) vuông tại B. \( \Rightarrow {S_{OAB}} = \frac{{OB.AB}}{2} = \frac{{R.2R}}{2} = {R^2}\). Xét tam giác OAB và tam giác OAC có: \(\left. {\begin{array}{*{20}{l}}{OB = OC{\mkern 1mu} {\mkern 1mu} \left( { = R} \right)}\\{AO{\mkern 1mu} {\mkern 1mu} chung}\\{\hat B = \hat C = {{90}^0}}\end{array}} \right\} \Rightarrow \Delta OAB = \Delta OAC\) (cạnh huyền – cạnh góc vuông) \( \Rightarrow {S_{OAB}} = {S_{OAC}} = {R^2}\) \( \Rightarrow {S_{ABOC}} = {S_{OAB}} + {S_{OAC}} = {R^2} + {R^2} = 2{R^2}\). c) Ta có \(MK \bot AC{\mkern 1mu} {\mkern 1mu} \left( {gt} \right) \Rightarrow \angle AKC = {90^0}\) \(MH \bot BC{\mkern 1mu} {\mkern 1mu} \left( {gt} \right) \Rightarrow \angle MHC = {90^0}\) \(\angle AKC + \angle HMC = {90^0} + {90^0} = {180^0}\) \( \Rightarrow \) Tứ giác MKCH là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)). \( \Rightarrow \angle MCK = \angle MHK\) (2 góc nội tiếp cùng chắn cung MK). Mà \(\angle MCK = \angle MBC = \angle MBH\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung MC). \(\angle MBH = \angle MIH\) (2 góc nội tiếp cùng chắn cung MH) \( \Rightarrow \angle MHK = \angle MIH{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)\) Chứng minh tương tự ta có: \(\angle MHI = \angle MBI\) (2 góc nội tiếp cùng chắn cung MI). Mà \(\angle MBI = \angle MCB = \angle MCH\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BM). \(\angle MCH = \angle MKH\) (2 góc nội tiếp cùng chắn cung MH) \( \Rightarrow \angle MHI = \angle MKH{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)\) Xét \(\Delta MHI\) và \(\Delta MKH\) có: $\begin{array}{*{35}{l}}\angle MIH=\angle MHK\left( theo\left( 1 \right) \right) \\ \angle MHI=\angle MKH\left( theo\left( 2 \right) \right) \\ \Rightarrow \Delta MHI\backsim \Delta MKH\left( g.g \right) \\ \end{array}$ \( \Rightarrow \frac{{MH}}{{MK}} = \frac{{MI}}{{MH}}\) (cặp cạnh tương ứng tỉ lệ). \( \Rightarrow MI.MK = M{H^2}{\mkern 1mu} {\mkern 1mu} \left( {dpcm} \right)\). Câu 6 (VDC): Phương pháp: Biến đổi biểu thức M về dạng xuất hiện a.b Áp dụng bất đẳng thức Cosi cho hai số dương: \(ab \le {\left( {\frac{{a + b}}{2}} \right)^2}\) Cách giải: Ta có: \(\begin{array}{l}M = \left( {1 - \frac{4}{{{a^2}}}} \right)\left( {1 - \frac{4}{{{b^2}}}} \right)\\M = \left( {\frac{{{a^2} - 4}}{{{a^2}}}} \right)\left( {\frac{{{b^2} - 4}}{{{b^2}}}} \right)\end{array}\) \(\begin{array}{l}M = \left( {\frac{{{a^2} - {{(a + b)}^2}}}{{{a^2}}}} \right)\left( {\frac{{{b^2} - {{(a + b)}^2}}}{{{b^2}}}} \right)\\M = \left( {\frac{{ - 2ab - {b^2}}}{{{a^2}}}} \right)\left( {\frac{{ - 2ab - {a^2}}}{{{b^2}}}} \right)\\M = \frac{{\left( {2a + b} \right)\left( { - b} \right)}}{{{a^2}}}.\frac{{\left( {a + 2b} \right)\left( { - a} \right)}}{{{b^2}}}\\M = \frac{{\left( {2a + b} \right)\left( {a + 2b} \right)}}{{ab}} = \frac{{\left( {a + a + b} \right)\left( {a + b + b} \right)}}{{ab}}\\M = \frac{{\left( {a + 2} \right)\left( {b + 2} \right)}}{{ab}} = \frac{{ab + 2\left( {a + b} \right) + 4}}{{ab}}\\M = \frac{{ab + 8}}{{ab}} = 1 + \frac{8}{{ab}}\end{array}\) Áp dụng bất đẳng thức Côsi ta có: \(\begin{array}{*{20}{l}}{ab \le {{\left( {\frac{{a + b}}{2}} \right)}^2} = {{\left( {\frac{2}{2}} \right)}^2} = 1}\\{ \Leftrightarrow \frac{8}{{ab}} \ge 8}\\{ \Leftrightarrow 1 + \frac{8}{{ab}} \ge 9}\\{ \Rightarrow M \ge 9}\end{array}\) Dấu “=” xảy ra \( \Leftrightarrow \) \(a = b = 1\). Vậy giá trị nhỏ nhất của M bằng 9 khi \(a = b = 1\).
|





















Danh sách bình luận