Đề số 42 - Đề thi vào lớp 10 môn Toán

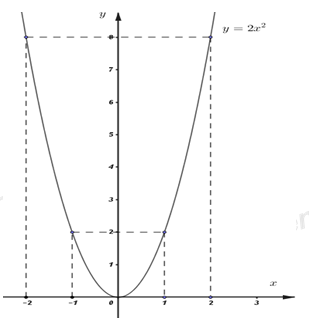
Đề bài

Bài 1 (2,5 điểm):

a)  Giải phương trình \({x^2} + 4x - 5 = 0.\)

b) Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x + y = 5\end{array} \right.\)

c)  Rút gọn biểu thức \(P = \sqrt {16}  - \sqrt[3]{8} + \dfrac{{\sqrt {12} }}{{\sqrt 3 }}.\)

Bài 2 (1,5 điểm): Cho parabol \(\left( P \right):\;\;y = 2{x^2}\) và đường thẳng \(\left( d \right):\;\;y = 2x + m\) (m là tham số).

a) Vẽ parabol \(\left( P \right).\)

b) Với những giá trị nào của \(m\) thì \(\left( P \right)\) và \(\left( d \right)\) chỉ có một điểm chung. Tìm tọa độ điểm chung đó.

Bài 3 (1,5 điểm):

a) Hai ô tô khởi hành cùng một lúc từ thành phố A đến thành phố B cách nhau 450 km với vận tốc không đổi. Vận tốc xe thứ nhất hơn vận tốc xe thứ hai 10 km/h nên xe thứ nhất đến thành phố B trước xe thứ hai 1,5 giờ. Tính vận tốc mỗi xe.

b) Cho phương trình: \({x^2} - mx - 1 = 0\) (m là tham số). Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) thỏa mãn \({x_1} < {x_2}\) và \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = 6.\)

Bài 4 (3,5 điểm): Cho đường tròn (O;R) và điểm A ở bên ngoài đường tròn đó.  Kẻ cát tuyến  AMN không đi qua O (M nằm giữa A và N). Kẻ hai tiếp tuyến AB, AC với (O;R) (B, C là hai tiếp điểm và C thuộc cung nhỏ MN). Đường thẳng BC cắt MN và AO lần lượt tại E, F. Gọi I là trung điểm của MN.

a)  Chứng minh tứ giác ABOC nội tiếp được trong đường tròn.

b)  Chứng minh \(EB.EC = EM.EN\) và IA là tia phân giác của góc \(\widehat {BIC}.\)

c)  Tia MF cắt (O;R) tại điểm thứ hai là D. Chứng minh \(\Delta AMF \sim \Delta AON\)  và  \(BC\parallel DN.\)

d)  Giả sử AO = 2R. Tính diện tích tam giác ABC theo R.

Bài 5 (1,0 điểm):

a) Giải phương trình: \(2\sqrt x  - \sqrt {3x + 1}  = x - 1.\)

b) Cho hai số thực dương \(a,\;b\) thỏa mãn \(a + b + 3ab = 1.\) Tìm giá trị lớn nhất của biểu thức \(P = \sqrt {1 - {a^2}}  + \sqrt {1 - {b^2}}  + \dfrac{{3ab}}{{a + b}}.\)

Lời giải chi tiết

Bài 1:

Giải phương trình \({x^2} + 4x - 5 = 0.\)

Ta có: \(a + b + c = 1 + 4 - 5 = 0\) Khi đó phương trình đã cho có 2 nghiệm phân biệt: \({x_1} = 1;{x_2} = \dfrac{c}{a} =  - 5.\)

Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ { - 5;1} \right\}\)

a)      Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x + y = 5\end{array} \right.\)

\(\left\{ \begin{array}{l}x - y = 1\\2x + y = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)

Vậy hệ phương trình có nghiệm là: \(\left( {x;y} \right) = \left( {2;1} \right)\)

b)     Rút gọn biểu thức \(P = \sqrt {16}  - \sqrt[3]{8} + \dfrac{{\sqrt {12} }}{{\sqrt 3 }}.\)

\(P = \sqrt {16}  - \sqrt[3]{8} + \dfrac{{\sqrt {12} }}{{\sqrt 3 }}\)\(\, = \sqrt {{4^2}}  - \sqrt[3]{{{2^3}}} + \sqrt {\dfrac{{12}}{3}}  \)\(\,= 4 - 2 + \sqrt {{2^2}}  = 2 + 2 = 4\)

Vậy P = 4.

Bài  2:

Cho parabol \(\left( P \right):\;\;y = 2{x^2}\) và đường thẳng \(\left( d \right):\;\;y = 2x + m\) (m là tham số).

a) Vẽ parabol \(\left( P \right).\)

Ta có bảng giá trị:

Vậy đồ thị hàm số \(\left( P \right):\;\;y = 2{x^2}\) là đường cong đi qua các điểm: \(\left( { - 2;\;8} \right),\;\;\left( { - 1;\;2} \right),\;\left( {0;\;0} \right),\;\;\left( {1;\;2} \right),\;\left( {2;\;8} \right).\)

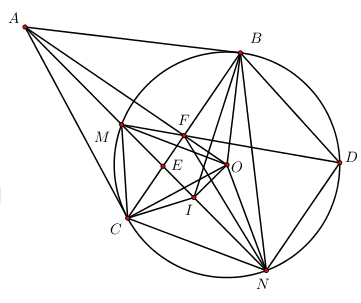
b) Với những giá trị nào của \(m\) thì \(\left( P \right)\) và \(\left( d \right)\) chỉ có một điểm chung. Tìm tọa độ điểm chung đó.

Phương trình hoành độ giao điểm của hai đồ thị hàm số là:

\(2{x^2} = 2x + m \\\Leftrightarrow 2{x^2} - 2x - m = 0\;\;\;\left( * \right)\)

Số giao điểm của đồ thị (P) và đường thẳng (d) cũng chính là số nghiệm của phương trình (*)

Đồ thị hàm số \(\left( P \right)\) và \(\left( d \right)\) chỉ có một điểm chung\( \Leftrightarrow \) phương trình \(\left( * \right)\) có nghiệm kép \( \Leftrightarrow \Delta ' = 0\)

\( \Leftrightarrow 1 + 2m = 0 \Leftrightarrow m =  - \dfrac{1}{2}.\)

Với \(m =  - \dfrac{1}{2}\) ta có:

\(\left( * \right) \Leftrightarrow 2{x^2} - 2x + \dfrac{1}{2} = 0\\ \Leftrightarrow 4{x^2} - 4x + 1 = 0 \\\Leftrightarrow {\left( {2x - 1} \right)^2} = 0\\ \Leftrightarrow x = \dfrac{1}{2}.\)

\( \Rightarrow y = 2.{\left( {\dfrac{1}{2}} \right)^2} = 2.\dfrac{1}{4} = \dfrac{1}{2} \Rightarrow \)tọa độ điểm chung của hai đồ thị là \(M\left( {\dfrac{1}{2};\;\dfrac{1}{2}} \right).\) 

Vậy với \(m =  - \dfrac{1}{2}\) thỏa mãn bài toán và điểm chung duy nhất của hai đồ thị là \(M\left( {\dfrac{1}{2};\;\dfrac{1}{2}} \right).\)

Bài 3:

a) Hai ô tô khởi hành cùng một lúc từ thành phố A đến thành phố B cách nhau 450 km với vận tốc không đổi. Vận tốc xe thứ nhất hơn vận tốc xe thứ hai 10 km/h nên xe thứ nhất đến thành phố B trước xe thứ hai 1,5 giờ. Tính vận tốc mỗi xe.

Gọi vận tốc của xe thứ nhất là \(x\;\left( {km/h} \right)\;\;\left( {x > 10} \right).\)

Khi đó vận tốc của xe thứ hai là: \(x - 10\;\;\left( {km/h} \right).\)

Thời gian xe thứ nhất và xe thứ hai đi hết quãng đường từ thành phố A đến thành phố B lần lượt là: \(\dfrac{{450}}{x}\;\left( h \right),\;\;\dfrac{{450}}{{x - 10}}\;\;\left( h \right).\)

Theo đề bài ta có phương trình: \(\dfrac{{450}}{{x - 10}} - \dfrac{{450}}{x} = 1,5\)

\(\begin{array}{l} \Leftrightarrow 300x - 300\left( {x - 10} \right) = x\left( {x - 10} \right)\\ \Leftrightarrow 300x - 300x + 3000 = {x^2} - 10x\\ \Leftrightarrow {x^2} - 10x - 3000 = 0\\ \Leftrightarrow \left( {x - 60} \right)\left( {x + 50} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 60 = 0\\x + 50 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 60\;\;\left( {tm} \right)\\x =  - 50\;\;\left( {ktm} \right)\end{array} \right..\end{array}\)

Vậy vận tốc của xe thứ nhất là \(60\;km/h,\) vận tốc của xe thứ hai là: \(60 - 10 = 50\;km/h.\)

b) Cho phương trình: \({x^2} - mx - 1 = 0\) (m là tham số). Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) thỏa mãn \({x_1} < {x_2}\) và \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = 6.\)

Phương trình đã cho có hai nghiệm phân biệt \({x_1},\;{x_2} \Leftrightarrow \Delta  > 0\)

\( \Leftrightarrow {m^2} + 4 > 0\;\;\left( {tm} \right)\forall m \in R.\)

\( \Rightarrow \) Phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của \(m.\)

Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} =  - 1\end{array} \right..\)

Ta có:

\(\begin{array}{l}{x_1}.{x_2} =  - 1 < 0 \Rightarrow {x_1} < 0 < {x_2}\\\left( {Do\,\,{x_1} < {x_2}} \right)\\ \Rightarrow \left| {{x_1}} \right| =  - {x_1};\left| {{x_2}} \right| = {x_2}\end{array}\)

Theo hệ thức bài cho ta có:

\(\begin{array}{l}\left| {{x_1}} \right| - \left| {{x_2}} \right| = 6\\ \Leftrightarrow  - {x_1} - {x_2} = 6\\ \Leftrightarrow {x_1} + {x_2} =  - 6\\ \Leftrightarrow m =  - 6\end{array}\)

Vậy \(m =  - 6\) thỏa mãn yêu cầu bài toán.

Bài 4.

Ch  đường tròn (O;R) và điểm A ở bên ngoài đường tròn đó.  Kẻ cát tuyến  AMN không đi qua O (M nằm giữa A và N). Kẻ hai tiếp tuyến AB, AC với (O;R) (B, C là hai tiếp điểm và C thuộc cung nhỏ MN). Đường thẳng BC cắt MN và AO lần lượt tại E, F. Gọi I là trung điểm của MN.

a)  Chứng minh tứ giác ABOC nội tiếp được trong đường tròn.

Ta có: AB, AC lần lượt là tiếp tuyến của đường tròn (O;R) nên: \(AC \bot OC \Rightarrow \angle ACO = {90^0};AB \bot OB \Rightarrow \angle ABO = {90^0}\)

Xét tứ giác ABOC ta có: \(\angle ACO + \angle ABO = {90^0} + {90^0} = {180^0}\)

Mà O và B là hai đỉnh đối nhau cùng nhìn cạnh OA các góc bằng nhau.

Nên tứ giác ABOC nội tiếp đường tròn đường kính OA và tâm là trung điểm của OA.

b)  Chứng minh \(EB.EC = EM.EN\) và IA là tia phân giác của góc \(\widehat {BIC}.\)

+) Chứng minh \(EB.EC = EM.EN\)

Xét tam giác ENC và tam giác EBM có:

\(\angle NEC = \angle MEB\) (hai góc đối đỉnh)

\(\angle CNE = \angle EBM\)  ( hai góc nội tiếp cùng chắn cung CM của đường tròn (O;R))

Vậy \(\Delta ENC \sim EBM\left( {g - g} \right)\)

Suy ra: \(\dfrac{{EN}}{{EB}} = \dfrac{{EC}}{{EM}} \Rightarrow EN.EM = EB.EC\) (đpcm)

+) Chứng minh IA là tia phân giác của góc \(\widehat {BIC}.\)

I là trung điểm của MN \( \Rightarrow OI \bot MN\) (quan hệ vuông góc giữa đường kính và dây cung)

\( \Rightarrow I\) thuộc đường tròn đường kính AO \( \Rightarrow I\) thuộc đường tròn ngoại tiếp tứ giác ABOC.

\( \Rightarrow \angle AIC = \angle ABC\) (hai góc nội tiếp cùng chắn cung AC)

\(\angle AIB = \angle ACB\) (hai góc nội tiếp cùng chắn cung AB).

Ta có \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)

\( \Rightarrow \Delta ABC\) cân tại A \( \Rightarrow \angle ABC = \angle ACB\) (hai góc ở đáy)

\( \Rightarrow \angle AIC = \angle AIB \Rightarrow AI\) là phân giác của \(\angle BIC\).

c)      Tia MF cắt \(\left( {O;R} \right)\) tại điểm thứ hai D. Chứng minh \(\Delta AMF \sim \Delta AON\) và BC // DN.

Chứng minh \(\Delta AMF \sim \Delta AON\)

Xét tam giác ACM và tam giác ANC có:

\(\angle CAN\) chung;

\(\angle ACM = \angle ANC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung CM);

\( \Rightarrow \Delta ACM \sim \Delta ANC\,\,\left( {g.g} \right)\)

\(\Rightarrow \dfrac{{AC}}{{AN}} = \dfrac{{AM}}{{AC}}\)

\(\Rightarrow A{C^2} = AM.AN\)

\(\Delta OAC\) vuông tại C \( \Rightarrow A{C^2} = AF.AO\) (hệ thức lượng trong tam giác vuông).

\( \Rightarrow AM.AN = AF.AO \Rightarrow \dfrac{{AM}}{{AO}} = \dfrac{{AF}}{{AN}}\)

Xét tam giác AMF và tam giác AON có:

\(\angle OAN\) chung;

\(\dfrac{{AM}}{{AO}} = \dfrac{{AF}}{{AN}}\,\,\left( {cmt} \right);\)

\( \Rightarrow \Delta AMF \sim \Delta AON\,\,\left( {c.g.c} \right)\).

Chứng minh BC // DN.

Ta có \(OB = OC = R;\,\,AB = AC\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow OA\) là trung trực của BC \( \Rightarrow OA \bot BC\).

Ta có: \(\Delta AMF \sim \Delta AON\,\,\left( {cmt} \right) \Rightarrow \angle AFM = \angle ANO\)

Mà \(\angle AMF + \angle OFM = {180^0}\) (kề bù) \( \Rightarrow \angle OFM + \angle ANO = {180^0} \Rightarrow \) Tứ giác OFMN là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰).

\( \Rightarrow \angle OFN = \angle OMN\) (hai góc nội tiếp cùng chắn cung ON).

Mà \(OM = ON \Rightarrow \Delta OMN\) cân tại O \( \Rightarrow \angle OMN = \angle ONM\)

\(\begin{array}{l} \Rightarrow \angle OFN = \angle ONM = \angle ONA = \angle AFM\\ \Rightarrow {90^0} - \angle OFN = {90^0} - \angle AFM\\ \Rightarrow \angle NFC = \angle MFC\\ \Rightarrow \angle MFC = \dfrac{1}{2}\angle MFN\end{array}\)

Mà \(\angle MFN = \angle MON\) (hai góc nội tiếp cùng chắn cung MN)

\( \Rightarrow \angle MFN = \dfrac{1}{2}\angle MON = \angle MDN\) (góc nội tiếp và góc ở tâm cùng chắn cun MN)

Hai góc này lại ở vị trí đồng vị \( \Rightarrow BC//DN\) .

d)     Giả sử \(AO = 2R\). Tính diện tích tam giác ABC theo R.

Áp dụng hệ thức lượng trong tam giác vuông OAC có

\(\begin{array}{l}O{C^2} = OF.OA\\ \Rightarrow OF = \dfrac{{O{C^2}}}{{OA}} = \dfrac{{{R^2}}}{{2R}} = \dfrac{R}{2}\\ \Rightarrow AF = AO - OF = 2R - \dfrac{R}{2} = \dfrac{{3R}}{2}\\C{F^2} = OF.AF = \dfrac{R}{2}.\dfrac{{3R}}{2} = \dfrac{{3{R^2}}}{4}\\ \Rightarrow CF = \dfrac{{R\sqrt 3 }}{2}\end{array}\)

Ta có \(OB = OC = R;\,\,AB = AC\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow OA\) là trung trực của BC \( \Rightarrow BC = 2CF = R\sqrt 3 \).

\(\begin{array}{l} \Rightarrow {S_{ABC}} = \dfrac{1}{2}AF.BC = \dfrac{1}{2}.\dfrac{{3R}}{2}.R\sqrt 3  = \dfrac{{3\sqrt 3 {R^2}}}{4}\\ \Rightarrow {S_{ABC}} = \dfrac{{3\sqrt 3 {R^2}}}{4}\end{array}\).

Bài 5. (1,0 điểm)

a) Giải phương trình \(2\sqrt x  - \sqrt {3x + 1}  = x - 1.\)

Cách 1:

Điều kiện \(x \ge 0\)

Đặt \(\left\{ \begin{array}{l}a = 2\sqrt x \\b = \sqrt {3x + 1} \end{array} \right.a,b \ge 0\)

Khi đó ta có: \({a^2} = 4x;{b^2} = 3x + 1\) \( \Rightarrow {a^2} - {b^2} = x - 1\) . Phương trình đã cho trở thành:

\(\begin{array}{l}a - b = {a^2} - {b^2} \\\Leftrightarrow \left( {a - b} \right)\left( {a + b - 1} \right) = 0 \\\Leftrightarrow \left[ \begin{array}{l}a = b\\a + b - 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2\sqrt x  = \sqrt {3x + 1} \\2\sqrt x  + \sqrt {3x + 1}  = 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}4x = 3x + 1\\4x + 3x + 1 + 4\sqrt {x\left( {3x + 1} \right)}  = 1\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = 1\left( {tm} \right)\\7x + 4\sqrt {x\left( {3x + 1} \right)}  = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {tm} \right)\\4\sqrt {x\left( {3x + 1} \right)}  =  - 7x\,\,\left( {do\,\,x \ge 0 \Rightarrow x = 0tm} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {tm} \right)\\x = 0\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy phương trình đã cho có nghiệm là x = 0; x = 1.

Cách 2:

a) Giải phương trình: \(2\sqrt x  - \sqrt {3x + 1}  = x - 1.\) Điều kiện: \(x \ge 0.\)

\(\begin{array}{l}\;\;\;\;\;2\sqrt x  - \sqrt {3x + 1}  = x - 1\\ \Leftrightarrow 2\sqrt x  - x + 1 = \sqrt {3x + 1} \end{array}\)

\(\begin{array}{l} \Leftrightarrow 4\sqrt x  - 2x + 2 = 2\sqrt {3x + 1} \\ \Leftrightarrow 3x + 1 + 1 - 2x + 4\sqrt x  + 2 = 3x + 1 + 2\sqrt {3x + 1}  + 1\\ \Leftrightarrow x + 4\sqrt x  + 4 = 3x + 1 + 2\sqrt {3x + 1}  + 1\\ \Leftrightarrow {\left( {\sqrt x  + 2} \right)^2} = {\left( {\sqrt {3x + 1}  + 1} \right)^2}\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt x  + 2 = \sqrt {3x + 1}  + 1\\\sqrt x  + 2 =  - \left( {\sqrt {3x + 1}  + 1} \right)\;\;\left( {VN} \right)\end{array} \right.\\ \Leftrightarrow \sqrt x  + 1 = \sqrt {3x + 1} \\ \Leftrightarrow x + 2\sqrt x  + 1 = 3x + 1\\ \Leftrightarrow 2x - 2\sqrt x  = 0\\ \Leftrightarrow 2\sqrt x \left( {\sqrt x  - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2\sqrt x  = 0\\\sqrt x  - 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\;\;\left( {tm} \right)\\x = 1\;\;\left( {tm} \right)\end{array} \right..\end{array}\)

Vậy phương trình có tập nghiệm \(S = \left\{ {0;\;1} \right\}.\)

b) Cho hai số thực dương \(a,\;b\) thỏa mãn \(a + b + 3ab = 1.\) Tìm giá trị lớn nhất của biểu thức \(P = \sqrt {1 - {a^2}}  + \sqrt {1 - {b^2}}  + \dfrac{{3ab}}{{a + b}}.\)

Áp dụng bất đẳng thức Cosi, ta có \(\left\{ \begin{array}{l}1 - {a^2} + \dfrac{8}{9} \ge 2\sqrt {\dfrac{8}{9}\left( {1 - {a^2}} \right)}  = \dfrac{{4\sqrt 2 }}{3}.\sqrt {1 - {a^2}} \\1 - {b^2} + \dfrac{8}{9} \ge 2\sqrt {\dfrac{8}{9}\left( {1 - {b^2}} \right)}  = \dfrac{{4\sqrt 2 }}{3}.\sqrt {1 - {b^2}} \end{array} \right.\)

Khi đó \(\dfrac{{4\sqrt 2 }}{3}.\left( {\sqrt {1 - {a^2}}  + \sqrt {1 - {b^2}} } \right) \le \dfrac{{17}}{9} - {a^2} + \dfrac{{17}}{9} - {b^2} = \dfrac{{34}}{9} - \left( {{a^2} + {b^2}} \right).\)

Ta có \(\dfrac{{1 - a - b}}{3} = ab \le \dfrac{{{{\left( {a + b} \right)}^2}}}{4}\)

\(\Leftrightarrow 3{\left( {a + b} \right)^2} + 4\left( {a + b} \right) - 4 \ge 0\)

\(\Leftrightarrow a + b \ge \dfrac{2}{3}.\)

Và \({a^2} + {b^2} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{2} \ge \dfrac{1}{2}.{\left( {\dfrac{2}{3}} \right)^2} = \dfrac{2}{9}\) suy ra \(\dfrac{{34}}{9} - \left( {{a^2} + {b^2}} \right) \le \dfrac{{32}}{9} \Rightarrow \sqrt {1 - {a^2}}  + \sqrt {1 - {b^2}}  \le \dfrac{{4\sqrt 2 }}{3}.\)

Lại có \(\dfrac{{3ab}}{{a + b}} = \dfrac{{1 - a - b}}{{a + b}} = \dfrac{1}{{a + b}} - 1\) mà \(a + b \ge \dfrac{2}{3} \)

\(\Leftrightarrow \dfrac{1}{{a + b}} \le \dfrac{3}{2}\) suy ra \(\dfrac{{3ab}}{{a + b}} \le \dfrac{3}{2} - 1 = \dfrac{1}{2}.\)

Do đó \(P = \sqrt {1 - {a^2}}  + \sqrt {1 - {b^2}}  + \dfrac{{3ab}}{{a + b}} \le \dfrac{{4\sqrt 2 }}{3} + \dfrac{1}{2}.\)

Dấu bằng xảy ra khi \(a = b = \dfrac{1}{3}.\)

Vậy \({P_{\max }} = \dfrac{{4\sqrt 2 }}{3} + \dfrac{1}{2}.\)

Loigiaihay.com