Đề thi vào 10 môn Toán Kiên Giang năm 2023Tải vềPhần I: Trắc nghiệm Câu 1: Giá trị của \(\sqrt {2023} \) bằng A. 17 B. 45 C. 44 D. \(17\sqrt 7 \) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
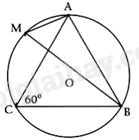
Đề bài Phần I: Trắc nghiệm Câu 1: Giá trị của \(\sqrt {2023} \) bằng A. 17 B. 45 C. 44 D. \(17\sqrt 7 \) Câu 2: Cho tam giác đều ABC nội tiếp trong đường tròn \((O),M\) là điểm thuộc \((O)\). Tính số đo của góc \(\angle AMB\) (tham khảo hình vẽ).
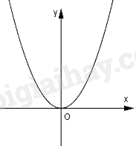
A. \(\angle AMB = 60^\circ \) B. \(\angle AMB = 75^\circ \) C. \(\angle AMB = 45^\circ \) D. \(\angle AMB = 30^\circ \) Câu 3: Trong các phương trình sau, phương trình nào là phương trình bậc hai ẩn \(x\)? A. \(2x - 3y = 0\) B. \(2x - 4 = 0\) C. \(2023 + 6x = 0\) D. \({x^2} - 16x + 3 = 0\) Câu 4: Chu vi của đường tròn có bán kính \(R\) được tính theo công thức \(C = 2\pi R\). Áp dụng tính chu vi của đường tròn \((T)\) có bán kính \(R = 2\;{\rm{m}}\). A. \(2\pi (m)\) B. \(2(\;m)\) C. \(4\pi (m)\) D. \(4(\;m)\) Câu 5: Trong các hàm số sau, hàm số nào luôn đồng biến trên \(\mathbb{R}\)? A. \(y = {\rm{ \;}} - 16x + 6\) B. \(y = 6x - 2023\) C. \(y = {\rm{ \;}} - x + 16\) D. \(y = 2023 - 6x\) Câu 6: Đồ thị của hàm số nào có dạng như hình vẽ?
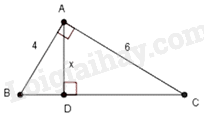
A. \(y = {x^2}\) B. \(y = 2x + 1\) C. \(y = 2\) D. \(y = x\) Câu 7: Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 1}\\{7x - y = 26}\end{array}} \right.\) có nghiệm là A. \((x;y) = (5; - 3)\) B. \((x;y) = ( - 5;3)\) C. \((x;y) = ( - 3;5)\) D. \((x;y) = (3; - 5)\) Câu 8: Cho hình trụ có bán kính đáy bằng \(R\), chiều cao là \(h\). Thể tích \(V\) của hình trụ đã cho được tính theo công thức A. \(V = \frac{4}{3}\pi {R^3}\) B. \(V = \frac{1}{3}\pi {R^2}h\) C. \(V = 2\pi Rh\) D. \(V = \pi {R^2}h\) Câu 9: Xác định hệ số a,b,c của phương trình bậc hai \({x^2} - 6x - 2023 = 0\). A. \(a = 1,b = 6,c = {\rm{ \;}} - 2023\) B. \(a = 1,b = 6,c = 2023\) C. \(a = 1,b = {\rm{ \;}} - 6,c = {\rm{ \;}} - 2023\) D. \(a = 0,b = {\rm{ \;}} - 6,c = {\rm{ \;}} - 2023\) Câu 10: Cho tam giác ABC vuông tại \(A\), biết \(AB = 4,AC = 6\), đường cao \(AD = x\) (tham khảo hình vẽ).
Hãy chọn công thức đúng? A. \({x^2} = {6^2} - {4^2}\) B. \(\frac{1}{{{x^2}}} = \frac{1}{{{4^2}}} - \frac{1}{{{6^2}}}\) C. \(\frac{1}{{{x^2}}} = \frac{1}{{{4^2}}} + \frac{1}{{{6^2}}}\) D. \({x^2} = {4^2} + {6^2}\) Câu 11: Biết phương trình bậc hai \({x^2} - 2023x + 2024 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Khi đó giá trị của tích \({x_1}{x_2}\) bằng A. 2023 B. -2023 C. -2024 D. 2024 Câu 12: Giá trị của hàm số \(y = 4{x^2}\) tại \(x = {\rm{ \;}} - 1\) bằng A. 4 B. -4 C. 1 D. -1 Câu 13: Trong World Cup 2022 được tổ chức tại Qatar, quả bóng được sử dụng cho các trận đấu có dạng hình cầu và có đường kính bằng \(22\;{\rm{cm}}\). Tính diện tích bề mặt của quả bóng.
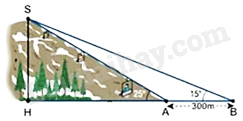
A. \(1936\pi \left( {c{m^2}} \right)\) B. \(121\pi \left( {c{m^2}} \right)\) C. \(484\pi \left( {c{m^2}} \right)\) D. \(576\pi \left( {c{m^2}} \right)\) Câu 14: Đường thẳng \(y = 3x - 2\) song song với đường thẳng nào sau đây? A. \(y = {\rm{ \;}} - 3x + 2\) B. \(y = 3x + 15\) C. \(y = 2x - 3\) D. \(y = {\rm{ \;}} - \frac{1}{3}x + 7\) Câu 15: Điều kiện của \(x\) để biểu thức \(\sqrt {x + 3} \) có nghĩa là A. \(x \le {\rm{ \;}} - 3\) B. \(x \ne {\rm{ \;}} - 3\) C. \(x > {\rm{ \;}} - 3\) D. \(x \ge {\rm{ \;}} - 3\) Phần II. Tự luận Câu 16: a) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức \(P = 2\sqrt {45} {\rm{ \;}} - 3\sqrt {20} \). b) Rút gọn biểu thức \(S = x \cdot \left( {\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}}} \right):\frac{x}{{{x^2} - 1}}\) với \(x \ne {\rm{ \;}} \pm 1\) và \(x \ne 0\). Câu 17: a) Không sử dụng máy tính cầm tay, giải phương trình \(2{x^2} - 3x - 5 = 0\). b) Để chuẩn bị cho kỳ thi Tuyển sinh vào lớp 10 THPT năm 2023, bạn Nam muốn mua một số bút bi và một số bút chì. Bạn Nam đến một cửa hàng và nhìn thấy trên giá có thông báo rằng nếu mua 5 bút bi xanh loại \(A\) và 3 bút chì loại 2B, bạn sẽ phải trả tổng cộng 38500 đồng. Nếu mua 2 bút bi xanh loại \(A\) và 4 bút chì loại 2B, tổng cộng sẽ là 28000 đồng. Hãy giúp bạn Nam tìm giá của mỗi bút bi xanh loại \(A\) và mỗi bút chì loại 2B. Câu 18: Cho parabol \((P):y = 2{x^2}\) và đường thẳng \((d):y = {\rm{ \;}} - 2x + 4\) a) Vẽ đồ thị \((P)\) trên hệ trục toạ độ Oxy. b) Tìm tọa độ các giao điểm của \((P)\) và \((d)\). Câu 19: Cho hình vuông ABCD cạnh \(AB = 16\;{\rm{cm}}\), lấy điểm \(H\) bất kỳ trên cạnh BC \((H\) khác \(B\) và \(C)\), qua \(B\) kẻ đường thẳng \((d)\) vuông góc với DH tại \(M\), gọi \(K\) là giao điểm của CD và \((d)\). a) Chứng minh rằng tứ giác BMCD nội tiếp trong một đường tròn. b) Chứng minh rằng KH vuông góc với BD. c) Gọi x, y lần lượt là diện tích của các tam giác HAB và HCD. Xác định vị trí của điểm \(H\) trên cạnh BC để \({x^2} + {y^2}\) đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó. Câu 20: Để xác định chiều dài của cáp treo trượt tuyết cần lắp đặt từ điểm \(A\) đến điểm \(S\), một nhân viên trắc địa đo được \(\angle SAH = 25^\circ \), sau đó anh ta đi xa ra một đoạn \(300\;m\) tới điểm \(B\) và đo được \(\angle SBH = 15^\circ \) (tham khảo hình vẽ). Tính chiều cao SH của núi (kết quả làm tròn là 2 chữ số thập phân).
----- HẾT ----- Lời giải chi tiết Phần I: Trắc nghiệm
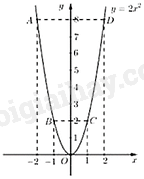
Câu 1 (NB): Phương pháp: Khai căn bậc hai. Cách giải: \(\sqrt {2023} {\rm{ \;}} = 17\sqrt 7 \) Chọn D. Câu 2 (NB): Phương pháp: Góc nội tiếp cùng chắn một cung có số đo bằng nhau. Cách giải: Ta có \(\angle ACB;\angle AMB\) cùng chắn cung AB. Vậy \(\angle ACB = \angle AMB = 60^\circ \) Chọn A. Câu 3 (NB): Phương pháp: Phương trình bậc hai ẩn \(x\) có dạng \(a{x^2} + bx + c = 0{\mkern 1mu} {\mkern 1mu} (a \ne 0)\) Cách giải: Phương trình bậc hai ẩn \(x\) là: \({x^2} - 16x + 3 = 0\) Chọn D. Câu 4 (NB): Phương pháp: Áp dụng công thức tính chu vi của đường tròn \(C = 2\pi R\). Cách giải: Áp dụng công thức có: \(C = 2.\pi .2 = 4\pi \) Chọn C. Câu 5 (NB): Phương pháp: Hàm số \(y = f(x)\) đồng biến nếu với mọi \({x_1};{x_2}\) thuộc tập xác định thỏa mãn \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\) Cách giải: Xét ý A: Lấy \({x_1},{x_2}\) là 2 số tùy ý sao cho \({x_1} < {x_2}\), ta có: \({x_1} < {x_2} \Rightarrow {\rm{ \;}} - 16{x_1} > {\rm{ \;}} - 16{x_2} \Rightarrow {\rm{ \;}} - 16{x_1} + 6 > {\rm{ \;}} - 16{x_2} + 6 \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\). Vậy hàm số nghịch biến Xét ý B: Lấy \({x_1},{x_2}\) là 2 số tùy ý sao cho \({x_1} < {x_2}\), ta có: \({x_1} < {x_2} \Rightarrow 6{x_1} < 6{x_2} \Rightarrow 6{x_1} - 2023 < 6{x_2} - 2023 \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\). Vậy hàm số đồng biến. Chọn B. Câu 6 (NB): Phương pháp: Dựa vào đồ thị. Cách giải: Đây là một đồ thị parabol, đi qua qua gốc tọa độ và đối xứng qua trục Oy. Đồ thị này là đồ thị của hàm số: \(y = {x^2}\) Chọn A. Câu 7 (NB): Phương pháp: Giải hệ phương trình bằng phương pháp cộng đại số. Cách giải: \(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{2x + y = 1}\\{7x - y = 26}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{9x = 27}\\{2x + y = 1}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{2.3 + y = 1}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = {\rm{ \;}} - 5}\end{array}} \right.}\end{array}\) Vậy hệ phương trình có nghiệm \((x;y) = (3; - 5)\) Chọn D. Câu 8 (NB): Phương pháp: Áp dụng công thức tính thể tích hình trụ. Cách giải: Thể tích \(V\) của hình trụ đã cho là: \(V = \pi {R^2}h\) Chọn D. Câu 9 (NB): Phương pháp: Phương trình bậc hai có dạng: \(a{x^2} + bx + c = 0(a \ne 0)\) Cách giải: Hệ số a,b,c của phương trình bậc hai \({x^2} - 6x - 2023 = 0\) là \(a = 1,b = {\rm{\;}} - 6,c = - 2023\) Chọn C. Câu 10 (NB): Phương pháp: Áp dụng công thức tính đường cao trong tam giác vuông. Cách giải: Xét tam giác ABC vuông tại A, có AD là đường cao \( \Leftrightarrow \frac{1}{{A{D^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)\( \Leftrightarrow \)\(\frac{1}{{{x^2}}} = \frac{1}{{{4^2}}} + \frac{1}{{{6^2}}}\) Chọn C. Câu 11 (NB): Phương pháp: Áp dụng định lí viet: Nếu phương trình bậc hai \(a{x^2} + bx + c = 0(a \ne 0)\) có hai nghiệm \({x_1};{x_2}\) thì tổng và tích của chúng là: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1},{x_2} = \frac{c}{a}\). Cách giải: Phương trình bậc hai \({x^2} - 2023x + 2024 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\). Khi đó giá trị của tích \({x_1}{x_2}\) bằng \(1 \cdot 2024 = 2024\) Chọn D. Câu 12 (NB): Phương pháp: Thay \(x = {\rm{ \;}} - 1\) vào hàm số \(y = 4{x^2}\) . Cách giải: Thay \(x = {\rm{ \;}} - 1\) vào hàm số \(y = 4{x^2}\) ta được \(y = 4 \cdot {( - 1)^2} = 4\) Chọn A. Câu 13 (VD): Phương pháp: Áp dụng công thức diện tích mặt cầu \(S = 4\pi {R^2}\) Cách giải: Đường kính bằng 22 cm nên bán kính \(R = 11\;cm\), diện tích mặt cầu là: \(S = 4\pi {R^2} = 4\pi {\rm{ \;}} \cdot {11^2} = 484\pi \left( {c{m^2}} \right)\) Chọn C. Câu 14 (TH): Phương pháp: Hai đường thẳng \(y = ax + b(a \ne 0)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi và chỉ khi \(a = a',b \ne b'\) . Cách giải: Đường thẳng \(y = 3x - 2\) song song với đường thẳng \(y = 3x + 15\). Chọn B. Câu 15 (TH): Phương pháp: \(\sqrt A \) có nghĩa khi \(A \ge 0\) Cách giải: \(\sqrt {x + 3} \) có nghĩa khi \(x + 3 \ge 0 \Leftrightarrow x \ge {\rm{ \;}} - 3\) Chọn D. Phần II. Tự luận Câu 16 (TH): Phương pháp: a) Khai căn b) Quy đồng rồi rút gọn Cách giải: a) Ta có \(P = 2\sqrt {45} {\rm{ \;}} - 3\sqrt {20} {\rm{ \;}} = 2\sqrt {9.5} {\rm{ \;}} - 3\sqrt {4.5} {\rm{ \;}} = 2.3\sqrt 5 {\rm{ \;}} - 3.2\sqrt 5 {\rm{ \;}} = 0\) Vậy \(P = 0\) b) Ta có \(\begin{array}{*{20}{l}}{S = x \cdot \left( {\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}}} \right):\frac{x}{{{x^2} - 1}}}\\{ = x\left( {\frac{{{{(x + 1)}^2}}}{{(x - 1)(x + 1)}} - \frac{{{{(x - 1)}^2}}}{{(x + 1)(x - 1)}}} \right):\frac{x}{{{x^2} - 1}}}\\{ = x \cdot \frac{{{x^2} + 2x + 1 - {x^2} + 2x - 1}}{{{x^2} - 1}}:\frac{x}{{{x^2} - 1}}}\\{ = \frac{{4{x^2}}}{{{x^2} - 1}} \cdot \frac{{{x^2} - 1}}{x}}\\{ = 4x}\end{array}\) Vậy \(S = 4x\) với \(x \ne {\rm{ \;}} \pm 1\) và \(x \ne 0\). Câu 17 (VD): Phương pháp: a) Xét hệ số a, b, c. b) Giải bài toán bằng cách lập hệ phương trình. Cách giải: a) Do \(a - b + c = 2 - ( - 3) + ( - 5) = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 1}\\{x = {\rm{ \;}} - \frac{{ - 5}}{2} = \frac{5}{2}}\end{array}} \right.\) Vậy phương trình có tập nghiệm \(S = \left\{ { - 1,\frac{5}{2}} \right\}\) b) Gọi số tiền mua 1 bút bi xanh loại \({\rm{A}}\) là \(x\left( {x \in {\mathbb{N}^*}} \right.\), đồng) Gọi số tiền mua 1 bút chì \(2\;{\rm{B}}\) là \(y\left( {y \in {\mathbb{N}^*}} \right.\), đồng) Do nếu mua 5 bút bi xanh loại \(A\) và 3 bút chì loại 2B, bạn sẽ phải trả tổng cộng 38500 đồng nên ta có phương trình \(5x + 3y = 38500\) Do mua 2 bút bi xanh loại \(A\) và 4 bút chỉ loại 2B, tổng cộng sẽ là 28000 đồng nên ta có phương trình \(2x + 4y = 28000\) Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x + 3y = 38500}\\{2x + 4y = 28000}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{20x + 12y = 154000}\\{6x + 12y = 84000}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{14x = 70000}\\{4y = 28000 - 2x}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 5000}\\{4y = 18000}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 5000}\\{y = 4500}\end{array}} \right.\) (thỏa mãn) Vậy 1 chiếc bút bi xanh có giá là 5000 đồng và 1 chiếc bút chì 2B có giá là 4500 đồng. Câu 18 (TH): Phương pháp: a) Vẽ đồ thị. b) Xét phương trình hoành độ giao điểm. Cách giải: TXĐ: \(D = \mathbb{R}.\) Ta có bảng giá trị sau:
\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O(0;0);{\mkern 1mu} {\mkern 1mu} A( - 2;8);{\mkern 1mu} {\mkern 1mu} B( - 1;2);\) \(C(1;2);{\mkern 1mu} {\mkern 1mu} D(2;8)\) Hệ số \(a = 2 > 0\) nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng. Ta vẽ được đồ thị hàm số \(y = 2{x^2}\) như sau:
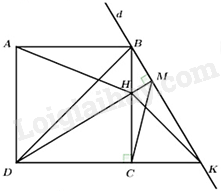
b) Xét phương trình hoành độ giao điểm của \((P)\) và \((d)\) ta được: \(\begin{array}{*{20}{l}}{2{x^2} = {\rm{ \;}} - 2x + 4}\\{ \Leftrightarrow 2{x^2} + 2x - 4 = 0}\\{ \Leftrightarrow {x^2} + x - 2 = 0}\end{array}\) Nhận thấy \(a + b + c = 1 + 1 + ( - 2) = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = \frac{c}{a} = {\rm{ \;}} - 2}\end{array}} \right.\). Với \(x = 1 \Rightarrow y = {2.1^2} = 2\) Với \(x = {\rm{ \;}} - 2 \Rightarrow y = 2.{( - 2)^2} = 8\) Vậy giao điểm của \((P)\) và \((d)\) có tọa độ là: \(C(1;2)\) và \(A( - 2;8)\). Câu 19 (VDC): Phương pháp: Áp dụng các tính chất hình học để chứng minh. Cách giải:
a) Ta có: \(\angle BMD = \angle BCD = 90^\circ \) (gt). Mà hai đỉnh M,C kề nhau cùng nhìn BD dưới một góc \(90^\circ \). \( \Rightarrow BMCD\) nội tiếp đường tròn đường kính BD (đpcm). b) Xét tam giác BDK có: \(\begin{array}{*{20}{l}}{BC \bot CD \Rightarrow BC \bot DK}\\{DH \bot d \Rightarrow DM \bot BK}\\{BC \cap DM = H}\end{array}\) \( \Rightarrow H\) là trực tâm của tam giác BDK. \( \Rightarrow KH \bot BD\) (đpcm) c) Ta có: \(\begin{array}{*{20}{l}}{x = {S_{{\rm{AHB}}}} = \frac{1}{2}AB \cdot BH = \frac{1}{2} \cdot 16 \cdot BH = 8BH}\\{y = {S_{{\rm{NHCD}}}} = \frac{1}{2}CD \cdot CH = \frac{1}{2} \cdot 16 \cdot CH = 8CH}\\{ \Rightarrow {x^2} + {y^2} = 64\left( {B{H^2} + C{H^2}} \right)}\end{array}\) Đặt \(BH = k{\mkern 1mu} {\mkern 1mu} (0 < k < 16) \Rightarrow CH = 16 - k\). Khi đó ta có \(\begin{array}{*{20}{l}}{B{H^2} + C{H^2} = {k^2} + {{(16 - k)}^2} = 2{k^2} - 32k + 256}\\{ = 2\left( {{k^2} - 16k + 64} \right) + 128 = 2{{(k - 8)}^2} + 128 \ge 128{\rm{ \;}}\forall 0 < k < 16}\\{ \Rightarrow {x^2} + {y^2} \ge 64.128 = 8192.}\end{array}\) Dấu “=” xảy ra khi \(k - 8 = 0 \Leftrightarrow k = 8\). Vậy \({x^2} + {y^2}\) đạt giá trị nhỏ nhất bằng 8192 khi \({\rm{k}} = 8\) hay \({\rm{H}}\) là trung điểm của \({\rm{BC}}\). Câu 20 (VDC): Phương pháp: Áp dụng hệ thức lượng trong tam giác. Cách giải: Đặt \(AH = x \Rightarrow BH = x + 300\) Áp dụng hệ thức lượng cho tam giác SHA và SHB vuông tại \(H\) ta được: \(\begin{array}{l}SH = AH \cdot \tan \widehat {SAH} = x \cdot \tan 25^\circ \\SH = BH \cdot \tan \widehat {SBH} = (x + 300) \cdot \tan 15^\circ \\ \Rightarrow x \cdot \tan 25^\circ = (x + 300) \cdot \tan 15^\circ \\ \Leftrightarrow x \cdot \tan 25^\circ = x \cdot \tan 15^\circ + 300 \cdot \tan 15^\circ \\ \Leftrightarrow x \cdot \left( {\tan 25^\circ - \tan 15^\circ } \right) = 300 \cdot \tan 15^\circ \\ \Leftrightarrow x = \frac{{300 \cdot \tan 15^\circ }}{{\tan 25^\circ - \tan 15^\circ }} \approx 405,25\end{array}\) Vậy chiều cao SH của núi là: \(405,25 \cdot \tan 25^\circ {\rm{\;}} \approx 188,97(\;m)\). -----HẾT-----
|






















Danh sách bình luận