Đề thi vào 10 môn Toán Kiên Giang năm 2019Tải vềI. Phần trắc nghiệm: 3,0 điểm (Gồm 15 câu hỏi trắc nghiệm một lựa chọn) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
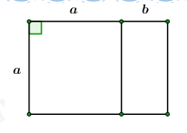
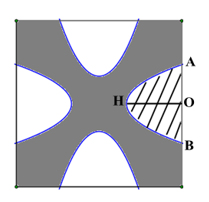
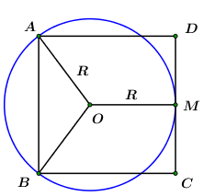
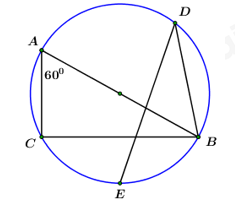
Đề bài I. Phần trắc nghiệm: 3,0 điểm (Gồm 15 câu hỏi trắc nghiệm một lựa chọn) Câu 1: Giá trị của \(\dfrac{{\sqrt {80} }}{{\sqrt 5 }}\) bằng: A. \(16\) B. \(4\sqrt 5 \) C. \(\sqrt 4 \) D. \(4\) Câu 2: Tính diện tích \(S\) của hình cầu có bán kính \(R = 12m.\) A. \(S = 2304\pi \,\,{m^2}\) B. \(S = 1296\pi \,\,{m^2}\) C. \(S = 576\pi \,\,{m^2}\) D. \(S = 144\pi \,\,{m^2}\) Câu 3: Cho các điểm sau, điểm nào không thuộc đồ thị của hàm số \(y = - 3x + 1?\) A. \(M\left( {1; - 4} \right)\) B. \(N\left( { - 1;\,\,4} \right)\) C. \(P\left( {2; - 5} \right)\) D. \(Q\left( {0;\,\,1} \right)\) Câu 4: Phương trình \({x^2} - 6x + 5 = 0\) có nghiệm là: A. \({x_1} = - 1;\,\,{x_2} = - 5\) B. \({x_1} = 1;\,\,{x_2} = 5\) C. \({x_1} = - 1;\,\,{x_2} = 5\) D. \({x_1} = 1;\,\,{x_2} = - 5\) Câu 5: Hệ phương trình \(\left\{ \begin{array}{l}2x + y = 5\\x = 1 + y\end{array} \right.\) có nghiệm là: A. \(\left( {x;\,\,y} \right) = \left( {2;\,1} \right)\) B. \(\left( {x;\,\,y} \right) = \left( {1;\,\,3} \right)\) C. \(\left( {x;\,\,y} \right) = \left( { - 2; - 1} \right)\) D. \(\left( {x;\,\,y} \right) = \left( {6;\,\,5} \right)\) Câu 6: Biết phương trình bậc hai \({x^2} - 2019x - 2020 = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\) Khi đó giá trị của tích \({x_1}{x_2}\) bằng: A. \( - 2019\) B. \(2019\) C. \( - 2020\) D. \(2020\) Câu 7: Tính thể tích \(V\) của hình trụ có bán kính đáy \(r = 3\) và chiều cao \(h = 10.\) A. \(V = 30\) B. \(V = 90\) C. \(V = 30\pi \) D. \(V = 90\pi \) Câu 8: Biểu thức \(P\left( x \right) = \sqrt {2019 - 3x} + x - 2020\) có nghĩa khi: A. \(x \ge 673\) B. \(x \le 673\) C. \(x < 2019\) D. \(x \ne 2020\) Câu 9: Tìm \(m\) để hai đường thẳng \({d_1}:\,\,\,y = 2mx + 3\) và \({d_2}:\,\,\,y = \left( {m + 1} \right)x + 2\) song song. A. \(m = 0\) B. \(m = 1\) C. \(m = - 1\) D. \(m = 2\) Câu 10: Người ta gọi tỉ lệ vàng \(\varphi = \dfrac{a}{b} = \dfrac{{a + b}}{a}.\) Tìm \(\varphi .\) A. \(\varphi = 2\) B. \(\varphi = \dfrac{3}{2}\) C. \(\varphi = \dfrac{{\sqrt 5 + 1}}{2}\) D. \(\varphi = \dfrac{{\sqrt 5 - 1}}{2}\) Câu 11: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh \(10cm\) bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết \(AB = 5cm,\,\,OH = 4cm\) và diện tích phần gạch sọc được tính theo công thức \(S = \dfrac{4}{3}OA.OH.\) Tính diện tích bề mặt hoa văn đó (phần hình được tô đen). A. \(\dfrac{{160}}{3}\,\,c{m^2}\) B. \(\dfrac{{140}}{3}\,\,c{m^2}\) C. \(\dfrac{{14}}{3}\,\,c{m^2}\) D. \(50\,\,c{m^2}\) Câu 12: Cho đường tròn \(\left( O \right)\) đi qua hai đỉnh \(A,\,\,B\) và tiếp xúc với cạnh \(CD\) của một hình vuông (tham khảo hình vẽ). Tính bán kính \(R\) của đường tròn đó biết cạnh hình vuông dài \(8cm.\) A. \(R = 4cm\) B. \(R = 6cm\) C. \(R = 4\sqrt 2 cm\) D. \(R = 5cm\) Câu 13: Máy kéo nông nghiệp có hai bánh sau to hơn bánh trước. Khi bơm căng, bánh xe sau có đường kính \(1,672\,\,m\) và bánh trước có đường kính là \(88cm.\) Hỏi khi xe chạy trên đoạn đường thẳng bánh xe sau lăn được \(10\) vòng thì bánh trước lăn được mấy vòng? A. 17 B. 18 C. 19 D. 20 Câu 14: Trong hình vẽ bên, biết \(AB\) là đường kính của đường tròn \(\left( O \right),\,\,E\) là điểm chính giữa của cung \(BC\) và \(\angle BAC = {60^0}.\) Tính số đo của \(\angle BDE.\) A. \(\angle BDE = {30^0}\) B. \(\angle BDE = {40^0}\) C. \(\angle BDE = {45^0}\) D. \(\angle BDE = {60^0}\) Câu 15: Nhân ngày Quốc tế thiếu nhi 1/6 vừa qua. Giáo viên chủ nhiệm lớp 9A phân công \(13\) học sinh (gồm \(x\) học sinh nam và \(y\) học sinh nữ) tham gia gói \(80\) phần quà cho các em thiếu nhi. Biết tổng số quà học sinh nam gói được bằng tổng số quà học sinh nữ gói được. Số quà mỗi bạn nam gói nhiều hơn số quà mỗi bạn nữ gói là \(3\) phần. Tính giá trị của \(P = 6x - 5y.\) A. \(P = 23\) B. \(P = 70\) C. \(P = - 70\) D. \(P = - 10\) II. Phần tự luận: 7,0 điểm Bài 1. (1,5 điểm) a) Thực hiện phép tính \(A = 3\sqrt {44} - 2\sqrt {99} \). b) Rút gọn biểu thức \(B = \dfrac{{\sqrt a + 1}}{{a\sqrt a + a + \sqrt a }}:\dfrac{1}{{{a^2} - \sqrt a }}\) với \(a > 0,\,\,a \ne 1\). Bài 2 (1,5 điểm) a) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 8\\x + 3y = 1\end{array} \right.\). b) Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} - 2x - m = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \({\left( {{x_1}{x_2} + 1} \right)^2} = 2\left( {x_1^2 + x_2^2} \right)\). Bài 3: (1,5 điểm) Cho parabol \(\left( P \right):\,\,y = - \dfrac{{{x^2}}}{4}\) và đường thẳng \(y = x + m\). a) Vẽ đồ thị \(\left( P \right)\) trên trục tọa độ \(Oxy\). b) Xác định tham số \(m\) để đường thẳng \(\left( d \right)\) và \(\left( P \right)\) có 1 điểm chung. Câu 4: Cho đường tròn tâm \(O\) bán kính \(R = 2019cm,\) có dây \(BC\) cố định \(\left( {BC < 2R} \right),\) \(A\) là một điểm trên cung lớn \(BC\) sao cho tam giác \(ABC\) có ba góc nhọn. Các đường cao \(BM\) và \(CN\) của tam giác \(ABC\) cắt nhau tại \(H\) (với \(M \in AC,\,\,N \in AB\)). a) Chứng minh tứ giác \(AMHN\) nội tiếp một đường tròn b) Tia \(AO\) cắt đường tròn \(\left( O \right)\) tại \(P.\) Chứng minh \(\angle BCN = \angle PAC\). c) Cho biết \(\angle BOC = 120^\circ .\) Tính độ dài đoạn \(AH.\) Bài 5 (0,75 điểm) Cầu Vàm Cống được khởi công ngày 10/9/2013, cầu có tổng chiều dài 2,97 km, phần cầu vượt sông dài 870m. Đây là cầu dây văng thứ 2 vượt song Hậu và là câu dây văng thứ 5 ở Miền Tây, nối liền hai tỉnh Cần Thơ và Đồng Tháp, với vốn đầu tư lên tới gần 5700 tỉ đồng, chính thức được thông xe vào ngày 19/5/2019, thông suốt toàn tuyến N2 từ Bình Phước về TP. Cần Thơ … Cầu được thiết kế với chiều cao từ sàn cầu đến đỉnh trụ đỡ \(AB = 120m\), dây văng \(AC = 258m\) , chiều dài sàn cầu từ B đến C là 218m (tham khảo hình vẽ). Hỏi góc nghiêng của sàn cầu BC so với mặt nằm ngang là bao nhiêu độ, phút, giây? (Giả thiết xem như trụ đỡ AB thẳng đứng). Lời giải I. Phần trắc nghiệm: 3,0 điểm (Gồm 15 câu hỏi trắc nghiệm một lựa chọn)
Câu 1- Liên hệ giữa phép chia và phép khai phương Phương pháp: Áp dụng công thức: \(\dfrac{{\sqrt A }}{{\sqrt B }} = \sqrt {\dfrac{A}{B}} \,\,\,\,\left( {A \ge 0,\,\,\,B > 0} \right).\) Cách giải: Ta có: \(\dfrac{{\sqrt {80} }}{{\sqrt 5 }} = \sqrt {\dfrac{{80}}{5}} = \sqrt {16} = 4.\) Chọn D. Câu 2 - Hình cầu - Diện tích mặt cầu và thể tích mặt cầu Phương pháp: Công thức tính diện tích hình cầu bán kính \(R\) là: \(S = 4\pi {R^2}.\) Cách giải: Ta có diện tích hình cầu là: \(S = 4\pi {R^2} = 4\pi {.12^2} = 576\pi \,\,{m^2}.\) Chọn C. Câu 3 - Hàm số bậc nhất Phương pháp: Thay tọa độ các điểm trong các đáp án vào công thức hàm số đã cho và chọn đáp án đúng. Cách giải: +) Xét điểm \(M\left( {1; - 4} \right)\) ta có: \( - 3.1 + 1 = - 2 \ne - 4 \Rightarrow M \notin \,\,d:\,\,y = - 3x + 1.\) Chọn A. Câu 4 - Phương trình bậc hai một ẩn số Phương pháp: Cách 1: Giải phương trình bằng cách đưa về phương trình tích. Cách 2: Nhẩm nghiệm của phương trình: \(a{x^2} + bx + c = 0\,\,\,\left( * \right)\) có: TH1: Nếu \(a + b + c = 0\) thì \(\left( * \right)\) có nghiệm \(x = 1\) và \(x = \dfrac{c}{a}.\) TH2: Nếu \(a - b + c = 0\) thì \(\left( * \right)\) có nghiệm \(x = - 1\) và \(x = - \dfrac{c}{a}.\) Cách 3: Thay các nghiệm ở các đáp án vào phương trình và chọn đáp án đúng. Cách giải: \(\begin{array}{l}{x^2} - 6x + 5 = 0 \Leftrightarrow {x^2} - 5x - x + 5 = 0\\ \Leftrightarrow x\left( {x - 5} \right) - \left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 1\end{array} \right..\end{array}\) Chọn B. Câu 5 - Giải hệ phương trình bằng phương pháp thế Phương pháp: Giải hệ phương trình bằng phương pháp thế. Cách giải: \(\begin{array}{l}\left\{ \begin{array}{l}2x + y = 5\\x = 1 + y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2\left( {1 + y} \right) + y = 5\\x = 1 + y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 + y\\2 + 2y + y = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1 + y\\3y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 + y\\y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\end{array}\) Chọn A. Câu 6 - Hệ thức Vi-ét và ứng dụng Phương pháp: Phương trình \(a{x^2} + bx + c = 0\,\,\,\,\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) thì theo hệ thức Vi-et ta có: \({x_1}.{x_2} = \dfrac{c}{a}.\) Cách giải: Giả sử \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 2019x - 2020 = 0\) Khi đó áp dụng định lý Vi-et ta có: \({x_1}{x_2} = - 2020.\) Chọn C. Câu 7 - Hình trụ - Diện tích xung quanh và thể tích của Hình trụ Phương pháp: Thể tích hình trụ có bán kính đáy \(R\) và chiều cao \(h\) là: \(V = \pi {R^2}h.\) Cách giải: Thể tích của hình trụ đã cho là: \(V = \pi {r^2}h = \pi {.3^2}.10 = 90\pi .\) Chọn D. Câu 8 - Căn thức bậc hai và hằng đẳng thức √A^(2)=|A| Phương pháp: Biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\) Cách giải: Biểu thức \(\sqrt {2019 - 3x} + x - 2020\) xác định \( \Leftrightarrow 2019 - 3x \ge 0 \Leftrightarrow x \le 673.\) Chọn B. Câu 9 - Đường thẳng song song và đường thẳng cắt nhau Phương pháp: Đường thẳng \(y = {a_1}x + {b_1}\) và \(y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Cách giải: Ta có: \({d_1}:\,\,\,y = 2mx + 3\) và \({d_2}:\,\,y = \left( {m + 1} \right)x + 2\) song song \( \Leftrightarrow \left\{ \begin{array}{l}2m = m + 1\\3 \ne 2\end{array} \right. \Leftrightarrow m = 1.\) Chọn B. Câu 10 - Ôn tập chương 4: Hàm số y = ax^2 (a ≠ 0) - Phương trình bậc hai một ẩn Phương pháp: Biến đổi và giải phương trình \(\dfrac{a}{b} = \dfrac{{a + b}}{a}\) với điều kiện \(a,\,\,b > 0.\) Cách giải: Điều kiện: \(a > 0,\,\,b > 0.\) Ta có: \(\varphi = \dfrac{a}{b} = \dfrac{{a + b}}{a}\) \(\begin{array}{l} \Leftrightarrow {a^2} = b\left( {a + b} \right) \Leftrightarrow {a^2} = ab + {b^2}\\ \Leftrightarrow {a^2} - ab - {b^2} = 0 \Leftrightarrow {\left( {\dfrac{a}{b}} \right)^2} - \dfrac{a}{b} - 1 = 0\,\,\,\,\,\left( * \right)\,\,\,\,\,\left( {do\,\,\,b > 0} \right)\end{array}\) Đặt \(\dfrac{a}{b} = t\,\,\,\left( {t > 0} \right)\) \( \Rightarrow \left( * \right) \Leftrightarrow {t^2} - t - 1 = 0\) Có: \(\Delta = {\left( { - 1} \right)^2} - 4.\left( { - 1} \right) = 5 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{t_1} = \dfrac{{1 + \sqrt 5 }}{2}\,\,\,\left( {tm} \right)\\{t_2} = \dfrac{{1 - \sqrt 5 }}{2}\,\,\,\left( {ktm} \right)\end{array} \right.\) \( \Rightarrow \varphi = \dfrac{a}{b} = \dfrac{{1 + \sqrt 5 }}{2}.\) Chọn C. Câu 11 - Bài tập ôn cuối năm Phương pháp: Diện tích hình vuông cạnh \(a\) là: \(S = {a^2}.\) Diện tích của phần hoa văn được tính bằng công thức: Diện tích hình vuông – 4 x diện tích phần gạch sọc. Cách giải: Diện tích của hình vuông đã cho là: \({10^2} = 100\,\,c{m^2}.\) Ta có: \(OA = \dfrac{1}{2}AB = \dfrac{1}{2}.5 = \dfrac{5}{2}\,\,cm.\) Khi đó diện tích phần gạch sọc là: \(S = \dfrac{4}{3}OA.OH = \dfrac{4}{3}.\dfrac{5}{2}.4 = \dfrac{{40}}{3}\,\,c{m^2}.\) Vậy diện tích bề mặt hoa văn là: \(100 - 4.\dfrac{{40}}{3} = \dfrac{{140}}{3}\,\,c{m^2}.\) Chọn B. Câu 12 - Ôn tập chương 2: Đường tròn Phương pháp: Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB = \left\{ H \right\}\) (mối liên hệ giữa đường kính và dây cung). Áp dụng định lý Pitago để làm bài. Cách giải: Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB = \left\{ H \right\}\) (mối liên hệ giữa đường kính và dây cung). \( \Rightarrow \left\{ \begin{array}{l}AH = AB\\MH = OM + OH\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AH = BH = 4\\8 = R + OH\end{array} \right..\) Đặt \(OH = x\,\,\left( {0 < x < 8} \right) \Rightarrow x = OH = 8 - R.\) Áp dụng định lý Pitago cho \(\Delta AOH\) vuông tại \(H\) ta có: \(\begin{array}{l}O{H^2} = A{O^2} - A{H^2} \Leftrightarrow {\left( {8 - R} \right)^2} = {R^2} - {4^2}\\ \Leftrightarrow 64 - 16R + {R^2} = {R^2} - 16\\ \Leftrightarrow 16R = 80 \Leftrightarrow R = 5\,\,cm.\end{array}\) Chọn D. Câu 13 - Ôn tập chương 3: Góc với đường tròn Phương pháp: Quãng đường đi được \(n\) của mỗi bánh xe là: \(2\pi R.n = \pi dn\) với \(R\) là bán kính và \(d\) là đường kính của bánh xe đó. Cách giải: Đổi: \(1,672m = 167,2\,\,cm.\) Khi đó quãng đường của bánh xe sau lăn được \(10\) vòng là: \(167,2\pi .10 = 1672\pi \,\,cm.\) Khi đó bánh trước lăn được số vòng là: \(1672\pi :88\pi = 19\) vòng. Chọn C. Câu 14 - Ôn tập chương 3: Góc với đường tròn Phương pháp: Hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau. Cách giải: Xét \(\left( O \right)\) ta có: \(\angle CAB\) là góc nội tiếp chắn cung \(BC\) Ta có \(E\) là điểm chính giữa cung \(BC\) Lại có: \(\angle EDB\) là góc nội tiếp chắn cung \(BE\) Chọn A. Câu 15 - Giải bài toán bằng cách lập hệ phương trình Phương pháp: Giải bài toán bằng cách lập hệ phương trình. Dựa vào các giả thiết bài cho, lập hệ gồm hai phương trình hai ẩn \(x,\,\,y\). Giải hệ phương trình vừa lập được để tìm \(x,\,\,y\) sau đó tính \(P.\) Cách giải: Gọi số bạn học sinh nam là \(x\,\,\left( {x \in {\mathbb{N}^*},\,\,\,x < 13} \right)\) (bạn). Gọi số bạn học sinh nữ là \(y\,\,\left( {y \in {\mathbb{N}^*},\,\,\,y < 13} \right)\) (bạn). Theo đề bài ta có: tổng số học sinh là \(13\) học sinh nên: \(x + y = 13\,\,\,\,\left( 1 \right)\) Tổng số phần quà là \(80\) phần quà và số phần quà các bạn nam gói được bằng số phần quà các bạn nữ gói được nên các bạn nam và các bạn nữ đều gói được \(80\) phần quà. Số phần quà mỗi bạn nam gói được là: \(\dfrac{{40}}{x}\) phần quà. Số phần quà mỗi bạn nữ gói được là: \(\dfrac{{40}}{y}\) phần quà. Số phần quà mỗi bạn nam gói được nhiều hơn số phần quà mỗi bạn nữ gói được nên ta có phương trình: \(\dfrac{{40}}{x} - \dfrac{{40}}{y} = 3\,\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right)\) ta có: \(y = 13 - x\) Thế vào \(\left( 2 \right)\) ta được: \(\left( 2 \right) \Leftrightarrow \dfrac{{40}}{x} - \dfrac{{40}}{{13 - x}} = 3\) \(\begin{array}{l} \Leftrightarrow 40\left( {13 - x} \right) - 40x = 3x\left( {13 - x} \right)\\ \Leftrightarrow 520 - 40x - 40x = 39x - 3{x^2}\\ \Leftrightarrow 3{x^2} - 119x + 520 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 5\,\,\,\left( {tm} \right)\\x = \dfrac{{104}}{3}\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) \( \Rightarrow \) Số bạn nữ là: \(y = 13 - 5 = 8\) bạn. \( \Rightarrow P = 6x - 5y = 6.5 - 5.8 = - 10.\) Chọn D. II. Phần tự luận: 7,0 điểm Bài 1 - Ôn tập chương 1: Căn bậc hai. Căn bậc ba Phương pháp: a) Sử dụng công thức \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \,\,\left( {B \ge 0} \right)\). b) Phân tích đa thức thành nhân tử, rút gọn. Cách giải: a) Thực hiện phép tính \(A = 3\sqrt {44} - 2\sqrt {99} \). \(\begin{array}{l}A = 3\sqrt {44} - 2\sqrt {99} = 3\sqrt {{2^2}.11} - 2\sqrt {{3^2}.11} \\\,\,\,\,\, = 3.2\sqrt {11} - 2.3\sqrt {11} = 6\sqrt {11} - 6\sqrt {11} = 0\end{array}\) b) Rút gọn biểu thức \(B = \dfrac{{\sqrt a + 1}}{{a\sqrt a + a + \sqrt a }}:\dfrac{1}{{{a^2} - \sqrt a }}\) với \(a > 0,\,\,a \ne 1\). Với \(a > 0,\,\,a \ne 1\) ta có: \(\begin{array}{l}B = \dfrac{{\sqrt a + 1}}{{a\sqrt a + a + \sqrt a }}:\dfrac{1}{{{a^2} - \sqrt a }}\\B = \dfrac{{\sqrt a + 1}}{{\sqrt a \left( {a + \sqrt a + 1} \right)}}.\sqrt a \left( {a\sqrt a - 1} \right)\\B = \dfrac{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)\left( {a + \sqrt a + 1} \right)}}{{a + \sqrt a + 1}}\\B = \left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right) = a - 1\end{array}\) Bài 2 a) - Giải hệ phương trình bằng phương pháp cộng đại số b) - Hệ thức Vi-ét và ứng dụng Phương pháp: a) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số. b) Tìm điều kiện để phương trình có 2 nghiệm phân biệt. Áp dụng định lí Vi-ét. Cách giải: a) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 8\\x + 3y = 1\end{array} \right.\). \(\left\{ \begin{array}{l}2x + 3y = 8\\x + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 7\\x + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 7\\7 + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 7\\y = - 2\end{array} \right.\). Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {7; - 2} \right)\). b) Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} - 2x - m = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \({\left( {{x_1}{x_2} + 1} \right)^2} = 2\left( {x_1^2 + x_2^2} \right)\). Ta có: \(\Delta ' = 1 - 1.\left( { - m} \right) = m + 1\). Để phương trình có 2 nghiệm phân biệt thì \(\Delta ' > 0 \Leftrightarrow m + 1 > 0 \Leftrightarrow m > - 1\). Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = - m\end{array} \right.\). Theo bài ra ta có: \({\left( {{x_1}{x_2} + 1} \right)^2} = 2\left( {x_1^2 + x_2^2} \right)\) \(\begin{array}{l} \Leftrightarrow {\left( {{x_1}{x_2} + 1} \right)^2} = 2\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] \Leftrightarrow {\left( { - m + 1} \right)^2} = 2\left[ {4 - 2.\left( { - m} \right)} \right]\\ \Leftrightarrow {m^2} - 2m + 1 = 8 + 4m \Leftrightarrow {m^2} - 6m - 7 = 0 \Leftrightarrow {m^2} + m - 7m - 7 = 0\\ \Leftrightarrow m\left( {m + 1} \right) - 7\left( {m + 1} \right) = 0 \Leftrightarrow \left( {m + 1} \right)\left( {m - 7} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = - 1\,\,\,\left( {ktm} \right)\\m = 7\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy \(m = 7\) thỏa mãn yêu cầu bài toán. Bài 3 - Ôn tập tổng hợp chương 2, 3, 4 - Đại số Phương pháp: a) Lập bảng giá trị và vẽ đồ thị hàm số. b) Xét phương trình hoành độ giao điểm. Tìm điều kiện để phương trình có 1 nghiệm. Cách giải: a) Vẽ đồ thị \(\left( P \right)\) trên trục tọa độ \(Oxy\). Bảng giá trị:
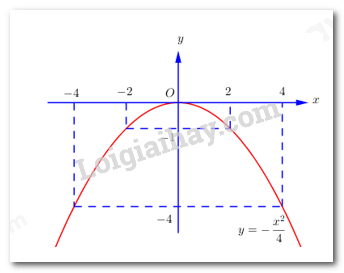
\( \Rightarrow \left( P \right):\,\,y = - \dfrac{{{x^2}}}{4}\) là parabol đi qua các điểm \(\left( { - 4; - 4} \right);\,\,\left( { - 2; - 1} \right);\,\,\left( {0;0} \right);\,\,\left( {2; - 1} \right);\,\,\left( {4; - 4} \right)\) và nhận Oy làm trục đối xứng. Vẽ đồ thị hàm số:
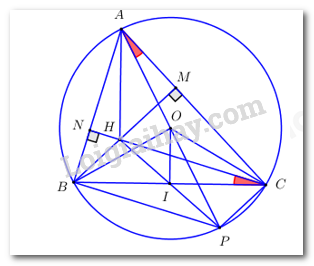
b) Xác định tham số \(m\) để đường thẳng \(\left( d \right)\) và \(\left( P \right)\) có 1 điểm chung. Xét phương trình hoành độ giao điểm: \( - \dfrac{{{x^2}}}{4} = x + m \Leftrightarrow {x^2} + 4x + 4m = 0\) (*) Để đường thẳng \(\left( d \right)\) và \(\left( P \right)\) có 1 điểm chung thì phương trình (*) có nghiệm duy nhất \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' = 0\end{array} \right.\). \( \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\,\,\,\left( {luon\,\,dung} \right)\\4 - 4m = 0\end{array} \right. \Leftrightarrow m = 1\). Vậy \(m = 1\) thỏa mãn yêu cầu bài toán. Bài 4 - Ôn tập tổng hợp chương 1, 2, 3 - Hình học Phương pháp: a) Chỉ ra tứ giác có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp b) Chứng minh \(CH//BP\) rồi sử dụng dụng tính chất hai đường thẳng song song và tính chất góc nội tiếp c) Sử dụng tính chất hình bình hành, tính chất đường trung bình của tam giác và quan hệ giữa cạnh và góc trong tam giác vuông. Cách giải: Cho đường tròn tâm \(O\) bán kính \(R = 2019cm,\) có dây \(BC\) cố định \(\left( {BC < 2R} \right),\) \(A\) là một điểm trên cung lớn \(BC\) sao cho tam giác \(ABC\) có ba góc nhọn. Các đường cao \(BM\) và \(CN\) của tam giác \(ABC\) cắt nhau tại \(H\) (với \(M \in AC,\,\,N \in AB\)). a) Chứng minh tứ giác \(AMHN\) nội tiếp một đường tròn Xét tam giác \(ABC\) có \(BM,CN\) là hai đường cao nên \(BM \bot AC,\,\,CN \bot AB \Rightarrow \angle ANH = \angle AMH = 90^\circ \). Xét tứ giác \(AMNH\) có \(\angle ANH + \angle AMH = 90^\circ + 90^\circ = 180^\circ \) mà hai góc ở vị trí đối nhau nên tứ giác \(AMHN\) là tứ giác nội tiếp (dhnb). b) Tia \(AO\) cắt đường tròn \(\left( O \right)\) tại \(P.\) Chứng minh \(\angle BCN = \angle PAC\) Xét đường tròn \(\left( O \right)\) có \(\angle ABP = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(BP \bot AB\). Lại có \(CN \bot AB\left( {gt} \right)\) \( \Rightarrow CN//BP\). Suy ra \(\angle BCN = \angle CBP\) (1) (hai góc ở vị trí so le trong) Xét đường tròn \(\left( O \right)\) có \(\angle PAC = \angle CBP\) (2) (hai góc nội tiếp cùng chắn cung \(CP\)) Từ (1) và (2) suy ra \(\angle BCN = \angle PAC\) (đpcm) c) Cho biết \(\angle BOC = 120^\circ .\) Tính độ dài đoạn \(AH.\) Xét đường tròn \(\left( O \right)\) có \(\angle PCA = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(CP \bot AC\). Lại có \(BM \bot AC\,\,\left( {gt} \right)\) \( \Rightarrow BM//CP\). Mặt khác theo câu b) thì \(CN//BP\). Từ đó, tứ giác \(BHCP\) có \(\left\{ \begin{array}{l}BP//CH\,\\CP//BH\,\end{array} \right.\) nên \(BHCP\) là hình bình hành (dhnb) Gọi \(I\) là giao điểm của \(HP\) và \(BC\), khi đó \(I\) là trung điểm của \(HP\) và \(I\) là trung điểm của \(BC\) (vì \(BHCP\) là hình bình hành) Xét tam giác \(PAH\) có \(O\) là trung điểm \(AP,\,\,\,I\) là trung điểm \(PH\) nên \(OI\) là đường trung bình \(\Delta PAH\). Suy ra \(AH = 2OI\). Xét đường tròn \(\left( O \right)\) có \(I\) là trung điểm \(BC \Rightarrow OI \bot BC\) tại \(I\) (quan hệ giữa đường kính và dây) Xét \(\Delta OBC\) cân tại \(O\) (do \(OB = OC = R\)) có \(OI\) là đường cao nên \(OI\) cũng là đường phân giác của \(\angle BOC\) \( \Rightarrow \angle BOI = \dfrac{1}{2}\angle BOC = \dfrac{1}{2}.120^\circ = 60^\circ \) Xét tam giác \(BOI\) vuông tại \(I\) có \(OI = OB.\cos \angle BOI = 2019.\cos 60^\circ = \dfrac{{2019}}{2}\) Suy ra \(AH = 2OI = 2.\dfrac{{2019}}{2} = 2019.\) Vậy \(AH = 2019.\)
Câu 5 - Bài tập ôn cuối năm Phương pháp: +) Đặt \(CH = x\,\,\left( m \right)\) . +) Áp dụng định lí Pytago và tỉ số lượng giác của góc nhọn trong tam giác vuông. Cách giải: Đặt \(CH = x\,\,\left( m \right)\,\,\left( {DK:\,\,0 < x < 218} \right)\). Áp dụng định lí Pytago trong tam giác vuông \(BCH\) ta có: \(B{H^2} = B{C^2} - C{H^2} = {218^2} - {x^2} \Rightarrow BH = \sqrt {{{218}^2} - {x^2}} \,\,\left( m \right)\) \( \Rightarrow AH = AB + BH = 120 + \sqrt {{{218}^2} - {x^2}} \,\,\left( m \right)\). Áp dụng định lí Pytago trong tam giác vuông \(ACH\) ta có: \(\begin{array}{l}A{H^2} + C{H^2} = A{C^2} \Leftrightarrow {\left( {120 + \sqrt {{{218}^2} - {x^2}} } \right)^2} + {x^2} = {258^2}\\ \Leftrightarrow {120^2} + 240\sqrt {{{218}^2} - {x^2}} + {218^2} - {x^2} + {x^2} = {258^2}\\ \Leftrightarrow 240\sqrt {{{218}^2} - {x^2}} = {258^2} - {120^2} - {218^2} = 4640\\ \Leftrightarrow 3\sqrt {{{218}^2} - {x^2}} = 58 \Leftrightarrow 9\left( {{{218}^2} - {x^2}} \right) = 3364\\ \Leftrightarrow {218^2} - {x^2} = \dfrac{{3364}}{9} \Leftrightarrow {x^2} = {218^2} - \dfrac{{3364}}{9} = \dfrac{{424352}}{9}\\ \Leftrightarrow x \approx 217,14\,\,\left( m \right)\,\,\left( {tm} \right)\end{array}\) Trong tam giác vuông \(BCH\): \(\cos \angle BCH = \dfrac{{CH}}{{BC}} \approx \dfrac{{217,14}}{{218}} \approx 0,996 \Leftrightarrow \angle BCH \approx {5^0}5'17''\). Vậy góc nghiêng của sàn cầu BC so với mặt nằm ngang xấp xỉ 5 độ, 5 phút, 17 giây.
|




















Danh sách bình luận