Đề thi minh hoạ vào 10 môn Toán Long An năm 2025

Đề bài

Câu 1:

a) Tính \(L = 2\sqrt 5 {\rm{ \;}} + \sqrt {45} {\rm{ \;}} - \frac{1}{2}\sqrt {320} \)

b) Cho biểu thức \(M = \frac{{a\sqrt b {\rm{ \;}} + b\sqrt a }}{{\sqrt a {\rm{ \;}} + \sqrt b }}\) với \(a > 0,{\mkern 1mu} {\mkern 1mu} b > 0\). Hãy rút gọn biểu thức \(M\) và tính giá trị của biểu thức \(M\) tại \(a = 2,{\mkern 1mu} {\mkern 1mu} b = 8\)

Câu 2: Vẽ đồ thị hàm số \(y = 2{x^2}\)

Câu 3:

a) Giải phương trình: \(3{x^2} + 7x - 2 = 0\)

b) Cho phương trình \({x^2} + 7x - 10 = 0\). Không giải phương trình hãy tính giá trị của biểu thức \(A = x_1^2{x_2} + {x_1}x_2^2\) (với \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) là hai nghiệm của phương trình)

c) Tại một buổi biểu diễn văn nghệ nhằm gây quỹ từ thiện, ban tổ chức bán được 500 vé. Trong đó có hai loại vé: vé loại I giá 100000 đồng; vé loại II giá 75000 đồng. Tổng số tiền thu được từ bán vé là 44500000 đồng. Tính số vé bán ra của mỗi loại.

Câu 4: Phần mái nhà của một ngôi nhà có dạng hình nón (không có đáy) với đường kính đáy khoảng 12 mét và độ dài đường sinh khoảng 8,5 mét (Hình minh họa). Chi phí để làm phần mái lá đó là 250000 đồng/1m². Hỏi tổng chi phí để làm toàn bộ phần mái lá đó là bao nhiêu đồng?

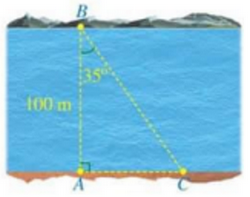
Câu 5:

1) Tính giá trị biểu thức $A = 4\sin 30^\circ \cos 30^\circ  + \tan 60^\circ$

2) Hình bên minh họa một phần con sông có bề rộng \(AB = 100\) mét. Một chiếc thuyền đi thẳng từ vị trí B bên này bờ sông đến vị trí C bên kia bờ sông. Tính quãng đường BC (làm tròn kết quả đến hàng phần mười của mét), biết $\angle ABC = 135^\circ$ 

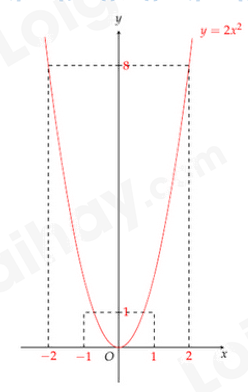
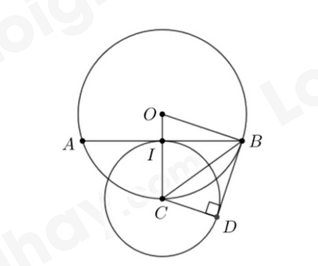
3) Cho đường tròn \(\left( O \right)\) và dây AB khác đường kính. Kẻ bán kính OC đi qua trung điểm \(I\) của đoạn thẳng AB. Vẽ đường tròn \(\left( {C;CI} \right)\). Kẻ tiếp tuyến BD của đường tròn \(\left( C \right)\) với \(D\) là tiếp điểm và \(D\) khác \(I\). Chứng minh:

a) Bốn đỉnh của tứ giác BDCI cùng nằm trên một đường tròn;

b) BD là tiếp tuyến của đường tròn \(\left( O \right)\)

Câu 6:

1) Trong bài thơ “Quê hương” của tác giả Đỗ Trung Quân có hai câu thơ:

“Quê hương nếu ai không nhớ

Sẽ không lớn nổi thằng người”

Mẫu dữ liệu thống kê các chữ cái in hoa \(H,{\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} G,{\mkern 1mu} {\mkern 1mu} L\) lần lượt xuất hiện trong hai câu thơ trên là \(H,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} G,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} H,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} G,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} H,{\mkern 1mu} {\mkern 1mu} H,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} G,{\mkern 1mu} {\mkern 1mu} L,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} H,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} H,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} G\). Lập bảng tần số tương đối của mẫu số liệu thống kê đó.

2) Cho tập hợp \(A = \left\{ {1;2} \right\}\) và \(B = \left\{ {0;3;4} \right\}\). Viết ngẫu nhiên một số tự nhiên có hai chữ số \(\overline {ab} \), trong đó \(a \in A,{\mkern 1mu} {\mkern 1mu} b \in B\).

a) Viết tập hợp \(\Omega \) gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra.

b) Tính xác suất của biến cố \(I\): “Số tự nhiên được viết ra là ước của 48”

Câu 7: Một nhà máy sản xuất xi măng mỗi ngày đều sản xuất được 100 tấn xi măng. Lượng xi măng tồn trong kho của nhà máy là 300 tấn. Hỏi nhà máy cần ít nhất bao nhiêu ngày để có thể xuất đi 15300 tấn xi măng (tính cả lượng xi măng tồn trong kho)?

----- HẾT -----

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM

Câu 1 (TH):

Phương pháp:

a) Đưa thừa số ra ngoài dấu căn và rút gọn.

b) Rút gọn sau đó thay \(a = 2,{\mkern 1mu} {\mkern 1mu} b = 8\) vào biểu thức M.

Cách giải:

a) Ta có: \(L = 2\sqrt 5 {\rm{ \;}} + \sqrt {45} {\rm{ \;}} - \frac{1}{2}\sqrt {320} {\rm{ \;}} = 2\sqrt 5 {\rm{ \;}} + 3\sqrt 5 {\rm{ \;}} - \frac{1}{2}.8\sqrt 5 {\rm{ \;}} = 2\sqrt 5 {\rm{ \;}} + 3\sqrt 5 {\rm{ \;}} - 4\sqrt 5 {\rm{ \;}} = \sqrt 5 \)

Vậy \(L = \sqrt 5 \)

b) Ta có: \(M = \frac{{a\sqrt b {\rm{ \;}} + b\sqrt a }}{{\sqrt a {\rm{ \;}} + \sqrt b }} = \frac{{\sqrt {ab} \left( {\sqrt a {\rm{ \;}} + \sqrt b } \right)}}{{\sqrt a {\rm{ \;}} + \sqrt b }} = \sqrt {ab} \)

Thay \(a = 2,{\mkern 1mu} {\mkern 1mu} b = 8\) vào \(M\) ta được \(M = \sqrt {2.8} {\rm{ \;}} = 4\)

Vậy \(M = 4\) với \(a = 2,{\mkern 1mu} {\mkern 1mu} b = 8\)

Câu 2 (NB):

Phương pháp:

Cho bảng giá trị và vẽ đồ thị hàm số.

Cách giải:

Bảng giá trị:

Đồ thị hàm số \(y = 2{x^2}\) có dạng parabol đi qua các điểm \(\left( { - 2;8} \right),{\mkern 1mu} {\mkern 1mu} \left( { - 1;1} \right),{\mkern 1mu} {\mkern 1mu} \left( {0;0} \right),{\mkern 1mu} {\mkern 1mu} \left( {1;1} \right),{\mkern 1mu} {\mkern 1mu} \left( {2;8} \right)\)

Đồ thị hàm số:

Câu 3 (TH):

Phương pháp:

a) Xét \(\Delta \) và suy ra nghiệm của phương trình.

b) Áp dụng hệ thức Viète.

c) Gọi số vé loại I, loại II lần lượt là \(x,{\mkern 1mu} {\mkern 1mu} y\) (vé, \(x,y \in \mathbb{N}*\))

Từ đó biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

Cách giải:

a) Ta có: \(\Delta {\rm{ \;}} = {7^2} - 4.3.\left( { - 2} \right) = 73\)

Phương trình có hai nghiệm phân biệt \({x_1} = \frac{{ - 7 + \sqrt {73} }}{6},{\mkern 1mu} {\mkern 1mu} {x_2} = \frac{{ - 7 - \sqrt {73} }}{6}\)

Vậy phương trình có hai nghiệm phân biệt \({x_1} = \frac{{ - 7 + \sqrt {73} }}{6},{\mkern 1mu} {\mkern 1mu} {x_2} = \frac{{ - 7 - \sqrt {73} }}{6}\)

b) Ta có: \(ac = 1.\left( { - 10} \right) = {\rm{ \;}} - 10 < 0\)

Do đó phương trình đã cho có 2 nghiệm phân biệt

Theo định lí Viète ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - 7}\\{{x_1}{x_2} = {\rm{ \;}} - 10}\end{array}} \right.\)

Khi đó \(A = x_1^2{x_2} + {x_1}x_2^2 = {x_1}{x_2}\left( {{x_1} + {x_2}} \right) = {\rm{ \;}} - 10. - 7 = 70\)

Vậy \(A = 70\)

c) Gọi số vé loại I, loại II lần lượt là \(x,{\mkern 1mu} {\mkern 1mu} y\) (vé, \(x,y \in \mathbb{N}*\))

Vì tổng số vé bán ra là 500 vé nên ta có \(x + y = 500{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)

Vì vé loại I giá 100000 đồng; vé loại II giá 75000 đồng, tổng số tiền thu được từ bán vé là 44500000 đồng nên ta có \(100000x + 75000y = 44500000{\mkern 1mu} {\mkern 1mu} \left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 500}\\{100000x + 75000y = 44500000}\end{array}} \right.\)

\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{x + y = 500}\\{100000x + 75000y = 44500000}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x + y = 500}\\{4x + 3y = 1780}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{4x + 4y = 2000}\\{4x + 3y = 1780}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{y = 220}\\{4x + 3.220 = 1780}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x = 280}\\{y = 220}\end{array}} \right.}\end{array}\)

Vậy số vé loại I, loại II lần lượt là 280 vé, 220 vé.

Câu 4 (TH):

Phương pháp:

Áp dụng công thức tính diện tích xung quanh: \(S = \pi rl\).

Cách giải:

Bán kính của đáy là \(12:2 = 6\left( m \right)\)

Diện tích xung quanh của mái lá hình nón là \(S = \pi rl = \pi .6.8,5 = 51\pi \left( {{m^2}} \right)\)

Chi phí để lợp mái là \(250000.51\pi {\rm{ \;}} = 40055000\) (đồng)

Câu 5 (VD):

Phương pháp:

1) Dựa vào bảng tỉ số lượng giác của các góc đặc biệt.

2) Sử dụng tỉ số lượng giác của góc nhọn.

3) Vận dụng các tính chất hình học để chứng minh.

Cách giải:

1) Ta có: $A = 4\sin 30^\circ \cos 30^\circ  + \tan 60^\circ  = 4.\dfrac{1}{2}.\dfrac{{\sqrt 3 }}{2} + \sqrt 3  = 2\sqrt 3$

2) Áp dụng định lí cosin trong tam giác ABC vuông tại $A$ ta có

$\cos \angle ABC = \dfrac{{AB}}{{BC}} \Rightarrow \cos 35^\circ  = \dfrac{{100}}{{BC}} \Rightarrow BC = 100\cos 35^\circ  \approx 81,9\left( m \right)$

Vậy quãng đường BC là \(81,9\left( m \right)\)

3)

a)

Ta có: \(I\) là trung điểm của dây cung AB

Suy ra $OI \bot AB$ (theo tính chất) hay $\angle BIC = 90^\circ$

Khi đó $B,\,\,I,\,\,C$ nội tiếp đường tròn đường kính BC (1)

Mặt khác $\angle BDC = 90^\circ$ (do BD là tiếp tuyến của $\left( {C;CI} \right)$) 

Suy ra \(B,{\mkern 1mu} {\mkern 1mu} D,{\mkern 1mu} {\mkern 1mu} C\) nội tiếp đường tròn đường kính BC (2)

Từ (1) và (2) suy ra \(B,{\mkern 1mu} {\mkern 1mu} D,{\mkern 1mu} {\mkern 1mu} C,{\mkern 1mu} {\mkern 1mu} I\) cùng thuộc đường tròn đường kính BC

b) Ta có: Tam giác OBC cân tại \(O\) (do \(OB = OC\))

\( \Rightarrow \angle OBC = \angle OCB{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)

Xét tam giác BIC vuông tại \(I\) và tam giác BDC vuông tại \(D\) có:

\(\begin{array}{*{20}{l}}{BC{\mkern 1mu} {\mkern 1mu} chung}\\{CI = CD}\\{ \Rightarrow \Delta BIC = \Delta BDC{\mkern 1mu} {\mkern 1mu} \left( {ch - cgv} \right)}\\{ \Rightarrow \angle IBC = \angle DBC{\mkern 1mu} {\mkern 1mu} \left( 2 \right)}\end{array}\)

Ta có: $\angle IBC + \angle ICB = 90^\circ \,\,\left( 3 \right)$

Từ (1), (2) và (3) suy ra $\angle OBC + \angle DBC = 90^\circ  \Rightarrow \angle OBD = 90^\circ$

Vậy BD là tiếp tuyến của \(\left( O \right)\)

Câu 6 (TH):

Phương pháp:

1) Đếm và lập bảng tần số, tần số tương đối.

2) Công thức tính xác suất: \(P\left( I \right) = \frac{{n\left( I \right)}}{{n\left( {\Omega {\rm{ \;}}} \right)}}\)

Cách giải:

1)

Bảng tần số tương đối của mẫu số liệu:

2)

a) \(\Omega {\rm{ \;}} = \left\{ {10;13;14;20;23;24} \right\}\)

b) Các kết quả thuận lợi của biến cố \(I\) là 24

Do đó có 1 kết quả thuận lợi của biến cố \(I\)

Vậy xác suất của biến cố \(I\) là \(P\left( I \right) = \frac{{n\left( I \right)}}{{n\left( {\Omega {\rm{ \;}}} \right)}} = \frac{1}{6}\)

Câu 7 (TH):

Phương pháp:

Gọi số ngày ít nhất nhà máy sản xuất 15300 tấn xi măng là \(x\) (ngày, \(x \in {\mathbb{N}^{\rm{*}}}\))

Từ đó phân tích đề bài và đưa ra bất phương trình.

Cách giải:

Gọi số ngày ít nhất nhà máy sản xuất 15300 tấn xi măng là \(x\) (ngày, \(x \in {\mathbb{N}^{\rm{*}}}\))

Số tấn xi măng \(x\) ngày, nhà máy sản xuất được: 100x (tấn)

Do nhà máy cần xuất 15300 tấn xi măng (tính cả lượng tồn trong kho) nên ta có: \(100x + 300 \ge 15300\)

Giải bất phương trình trên, ta có:

\(100x + 300 \ge 15300\)

\(100x \ge 15000\)

\(x \ge 150\)

Vậy nhà máy cần ít nhất 150 ngày để có thể xuất đi 15300 tấn xi măng.