Đề thi vào 10 môn Toán Bình Thuận năm 2019Tải vềCâu 1 (2 điểm): Giải phương trình và hệ phương trình sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
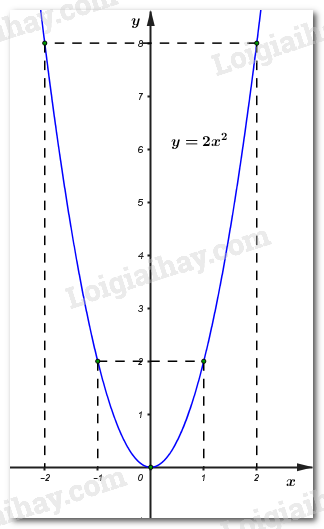
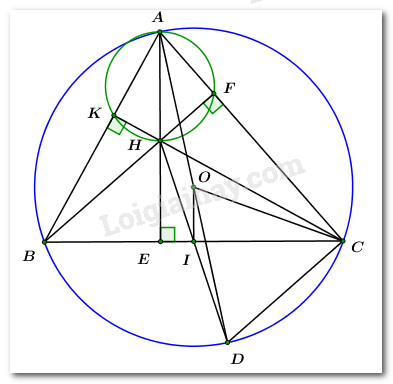
Đề bài Câu 1 (2 điểm): Giải phương trình và hệ phương trình sau: \(a)\,\,{x^2} + 3x - 10 = 0 & & & b)\,\,\left\{ \begin{array}{l}x + 3y = 6\\x - 2y = 1\end{array} \right..\) Câu 2 (1 điểm): Rút gọn biểu thức: \(M = \dfrac{{3\sqrt {75} - 12\sqrt 3 + \sqrt {12} }}{5}.\) Câu 3 (2 điểm): Cho hàm số \(y = 2{x^2}\) có đồ thị là \(\left( P \right).\) a) Vẽ đồ thị \(\left( P \right).\) b) Tìm tham số \(m\) để đường thẳng \(\left( d \right):\,\,\,y = mx - 2\) tiếp xúc với \(\left( P \right).\) Câu 4 (1 điểm): Một mảnh đất hình chữ nhật có hai lần chiều rộng bé hơn chiều dài là \(9m\) và diện tích bằng \(200{m^2}.\) Tính chu vi của mảnh đất. Câu 5 (4 điểm): Cho tam giác \(ABC\) có ba góc nhọn nội tiếp trong đường tròn \(\left( {O;\,\,R} \right),\,\,\left( {AB < AC} \right).\) Ba đường cao \(AE,\,\,BF\) và \(CK\) của tam giác \(ABC\) cắt nhau tại \(H.\) Vẽ đường kính \(AD\) của đường tròn \(\left( {O;\,\,R} \right).\) a) Chứng minh tứ giác \(AKHF\) nội tiếp. b) Chứng minh \(DC//BF.\) c) Chứng minh \(AB.AC = AE.AD.\) d) Cho \(BC = \dfrac{{4\sqrt 2 R}}{3}.\) Tính theo \(R\) diện tích hình tròn ngoại tiếp tam giác \(HKF.\) Câu 2 Câu 1 Phương pháp: a) Giải phương trình bằng công thức nghiệm. b) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số. Cách giải: \(a)\,\,{x^2} + 3x - 10 = 0\) Ta có: \(\Delta = {b^2} - 4ac = {3^2} + 4.10 = 49 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - 3 + \sqrt {49} }}{2} = 2\\{x_2} = \dfrac{{ - 3 - \sqrt {49} }}{2} = - 5\end{array} \right..\) Vậy tập nghiệm của phương trình là: \(S = \left\{ { - 5;\,\,2} \right\}.\) \(b)\,\,\left\{ \begin{array}{l}x + 3y = 6\\x - 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y = 5\\x = 1 + 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 1 + 2.1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right..\) Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\,\,y} \right) = \left( {3;\,\,1} \right).\) Câu 2 Phương pháp: Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Cách giải: \(\begin{array}{l}M = \dfrac{{3\sqrt {75} - 12\sqrt 3 + \sqrt {12} }}{5} = \dfrac{{3\sqrt {{5^2}.3} - 12\sqrt 3 + \sqrt {{2^2}.3} }}{5}\\\,\,\,\,\,\,\,\, = \dfrac{{3.5\sqrt 3 - 12\sqrt 3 + 2\sqrt 3 }}{5} = \dfrac{{5\sqrt 3 }}{5} = \sqrt 3 .\end{array}\) Câu 3 Phương pháp: a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ. b) Đường thẳng \(d\) tiếp xúc với parabol \(\left( P \right) \Leftrightarrow \) phương trình hoành độ giao điểm của hai đồ thị có nghiệm kép \( \Leftrightarrow \Delta = 0\,\,\left( {\Delta ' = 0} \right).\) Cách giải: Cho hàm số \(y = 2{x^2}\) có đồ thị là \(\left( P \right).\) a) Vẽ đồ thị \(\left( P \right).\) Ta có bảng giá trị:
Vậy đồ thị hàm số \(\left( P \right):\,\,\,y = 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;\,\,8} \right),\,\,\left( { - 1;\,2} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\,\,2} \right),\,\,\left( {2;\,\,8} \right)\) và nhận trục \(Oy\) làm trục đối xứng. b) Tìm tham số \(m\) để đường thẳng \(\left( d \right):\,\,\,y = mx - 2\) tiếp xúc với \(\left( P \right).\) Phương trình hoành độ giao điểm của hai đồ thị hàm số là: \(2{x^2} = mx - 2 \Leftrightarrow 2{x^2} - mx + 2 = 0\,\,\,\left( * \right)\) Đường thẳng \(d\) tiếp xúc với parabol \(\left( P \right) \Leftrightarrow \,\,\left( * \right)\) có nghiệm kép \( \Leftrightarrow \Delta = 0 \Leftrightarrow {m^2} - 4.2.2 = 0 \Leftrightarrow {m^2} = 16 \Leftrightarrow \left[ \begin{array}{l}m = 4\\m = - 4\end{array} \right..\) Vậy với \(m = 4\) hoặc \(m = - 4\) thì thỏa mãn bài toán. Câu 4 Phương pháp: Giải bài toán bằng cách lập phương trình. Gọi chiều rộng của mảnh đất là \(x\,\,\left( m \right),\,\,\,\left( {x > 0} \right).\) Biểu diễn chiều dài và diện tích của mảnh đất theo ẩn vừa gọi. Giải phương trình và đối chiếu với điều kiện rồi kết luận. Cách giải: Gọi chiều rộng của mảnh đất là \(x\,\,\left( m \right),\,\,\,\left( {x > 0} \right).\) Vì hai lần chiều rộng bé hơn chiều dài \(9m\) nên chiều dài của mảnh đất là: \(2x + 9\,\,\,\left( m \right).\) Diện tích của mảnh đất là \(200{m^2}\) nên ta có phương trình: \(x\left( {2x + 9} \right) = 200 \Leftrightarrow 2{x^2} + 9x - 200 = 0\) Có \(\Delta = {9^2} + 4.2.200 = 1681 > 0 \Rightarrow \sqrt \Delta = \sqrt {1681} = 41.\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - 9 + 41}}{{2.2}} = 8\,\,\,\,\left( {tm} \right)\\{x_2} = \dfrac{{ - 9 - 41}}{{2.2}} = - \dfrac{{25}}{2}\,\,\,\left( {ktm} \right)\end{array} \right.\) \( \Rightarrow \) Chiều rộng của mảnh đất là \(8m,\) chiều dài của mảnh đất là: \(2.8 + 9 = 25m.\) Vậy chu vi của mảnh đất là: \(\left( {8 + 25} \right).2 = 66\,m.\) Câu 5 Phương pháp: a) Sử dụng dấu hiệu nhận biết để chứng minh tứ giác nội tiếp. b) Chứng minh song song theo định lý từ vuông góc đến song song. c) Chứng minh cặp tam giác đồng dạng tương ứng rồi suy ra đẳng thức. d) Công thức tính diện tích hình tròn bán kính \(r:\,\,S = \pi {r^2}.\) Cách giải:
a) Chứng minh tứ giác \(AKHF\) nội tiếp. Ta có: \(\left\{ \begin{array}{l}\angle AKH = {90^{0\,}}\,\,\,\left( {CK \bot AB = \left\{ K \right\}} \right)\\\angle AFH = {90^0}\,\,\,\,\,\left( {BF \bot AC = \left\{ K \right\}} \right)\end{array} \right.\) Xét tứ giác \(AKHF\) ta có: \(\angle AKH + \angle AFH = {90^0} + {90^0} = {180^0}\) Mà hai góc này là hai góc đối nhau trong tứ giác \( \Rightarrow AKHF\) là tứ giác nội tiếp. (dhnb). b) Chứng minh \(DC//BF.\) Ta có: \(BF \bot AC\) (do \(BF\) là đường cao của \(\Delta ABC\)) Lại có: \(\angle ACD = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow CD \bot AC.\) \( \Rightarrow CD//BF\,\,\left( { \bot AC} \right)\) (từ vuông góc đến song song). c) Chứng minh \(AB.AC = AE.AD.\) Xét \(\Delta ABE\) và \(\Delta ADC\) ta có: \(\angle ABE = \angle ADC\) (hai góc nội tiếp cùng chắn cung \(AC\)) d) Cho \(BC = \dfrac{{4\sqrt 2 R}}{3}.\) Tính theo \(R\) diện tích hình tròn ngoại tiếp tam giác \(HKF.\) Theo câu a) ta có tứ giác \(AKHF\) là tứ giác nội tiếp. \( \Rightarrow \) đường tròn ngoại tiếp tam giác \(HKF\) là đường tròn \(\left( C \right)\) đi qua các điểm \(A,\,\,K,\,\,H,\,\,F.\) Lại có \(\Delta AKH\) là tam giác vuông tại \(K\) nội tiếp đường tròn \(\left( C \right)\) \( \Rightarrow AH\) là đường kính của đường tròn \(\left( C \right).\) Gọi \(I\) là trung điểm của \(BC\) ta có: \(OI \bot BC = \left\{ I \right\}\) (mối liên hệ giữa đường kính và dây cung). Mà \(AE \bot BC\,\,\left( {gt} \right) \Rightarrow OI//AE\,\,hay\,\,\,OI//AH\) (từ vuông góc đến song song). Lại có \(O\) là trung điểm của \(AD.\) \( \Rightarrow OI\) là đường trung bình của \(\Delta ADH.\) \( \Rightarrow OI = \dfrac{1}{2}AH \Leftrightarrow AH = 2OI.\) Áp dụng định lý Pitago trong \(\Delta IOC\) vuông tại \(I\) ta có: \(\begin{array}{l}OI = \sqrt {O{C^2} - I{C^2}} = \sqrt {O{C^2} - \dfrac{{B{C^2}}}{4}} = \sqrt {{R^2} - \dfrac{{{{\left( {4\sqrt 2 R} \right)}^2}}}{{4.9}}} = \dfrac{R}{3}.\\ \Rightarrow AH = 2OI = 2.\dfrac{R}{3} = \dfrac{{2R}}{3}.\end{array}\) Khi đó diện tích hình tròn ngoại tiếp tam giác \(HKF\) là: \(S = \pi .\dfrac{{A{H^2}}}{4} = \pi .{\left( {\dfrac{{2R}}{3}} \right)^2}.\dfrac{1}{4} = \dfrac{{\pi {R^2}}}{9}.\)
|














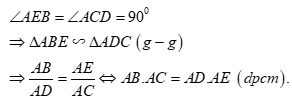






Danh sách bình luận