Đề thi vào 10 môn Toán Hòa Bình năm 2020Tải vềCâu I: 1) Tính giá trị các biểu thức sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
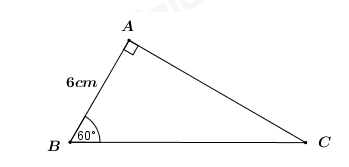
Đề bài Câu I: 1) Tính giá trị các biểu thức sau: a) \(A = \sqrt {16} + 5\) b) \(B = \sqrt 8 - \sqrt 2 \) 2) Giải các phương trình sau: a) \(\sqrt {x - 3} = 2\) b) \({x^2} - 4 = 0\) Câu II: 1) Trong mặt phẳng tọa độ \(Oxy\), cho hai đường thẳng \(\left( {{d_1}} \right):\,\,y = \left( {m - 1} \right)x + 2\) và \(\left( {{d_2}} \right):\,\,y = x - 3\). Tìm \(m\) để hai đường thẳng đã cho song song với nhau. 2) Cho phương trình \({x^2} + 4x + 2m + 1 = 0\) (\(m\) là tham số). a) Giải phương trình với \(m = 1\). b) Tìm \(m\) để phương trình có nghiệm kép. Câu III: 1) Cho tam giác \(ABC\) vuông tại \(A\), có \(AB = 6cm\), góc \(\angle ABC = {60^0}\). Tính chu vi tam giác \(ABC\). 2) Một chiếc ti vi giảm giá hai lần, mỗi lần giảm giá 10% so với giá đang bán, sau khi giảm giá 2 lần thì giá còn lại là 16 200 000 đồng. Hỏi giá ban đầu của chiếc ti vi là bao nhiêu? Câu IV: Cho tam giác nhọn \(ABC\) \(\left( {AB \ne AC} \right)\) có các đường cao \(AD,\,\,BE,\,\,CF\) cắt nhau tại H. 1) Chứng minh rằng: Tứ giác \(AEHF\) là tứ giác nội tiếp. 2) Chứng minh rằng: \(\angle ADE = \angle ADF\). 3) Chứng minh rằng: Đường tròn ngoại tiếp tam giác \(EDF\) đi qua trung điểm \(M\) của cạnh \(BC\). Câu V: 1) Tìm các số thực \(x,\,\,y,\,\,z\) thỏa mãn \({x^2} + {y^2} + 4{z^2} - 4x - 2y + 4z + 6 = 0\). 2) Cho các số thực \(x,\,\,y\) thỏa mãn \(x > 2y\) và \(xy = 3\).Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + 4{y^2} - 11}}{{x - 2y}}\). Lời giải Câu I (2,0 điểm) Cách giải: 1) Tính giá trị các biểu thức sau: a) \(A = \sqrt {16} + 5\) b) \(B = \sqrt 8 - \sqrt 2 \) a) \(A = \sqrt {16} + 5 = \sqrt {{4^2}} + 5 = 4 + 5 = 9\). Vậy \(A = 9\). b) \(B = \sqrt 8 - \sqrt 2 = \sqrt {{2^2}.2} - \sqrt 2 = 2\sqrt 2 - \sqrt 2 = \sqrt 2 \). Vậy \(B = \sqrt 2 \). 2) Giải các phương trình sau: a) \(\sqrt {x - 3} = 2\) b) \({x^2} - 4 = 0\) a) \(\sqrt {x - 3} = 2\) \( \Leftrightarrow x - 3 = 4 \Leftrightarrow x = 7\) Vậy tập nghiệm của phương trình là \(S = \left\{ 7 \right\}\). b) \({x^2} - 4 = 0\) \( \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\). Vậy tập nghiệm của phương trình là \(S = \left\{ { \pm 2} \right\}\). Câu II (2,0 điểm) Cách giải: 1) Trong mặt phẳng tọa độ \(Oxy\), cho hai đường thẳng \(\left( {{d_1}} \right):\,\,y = \left( {m - 1} \right)x + 2\) và \(\left( {{d_2}} \right):\,\,y = x - 3\). Tìm \(m\) để hai đường thẳng đã cho song song với nhau. Hai đường thẳng \(\left( {{d_1}} \right):\,\,y = \left( {m - 1} \right)x + 2\) và \(\left( {{d_2}} \right):\,\,y = x - 3\) song song với nhau khi và chỉ khi \(\left\{ \begin{array}{l}m - 1 = 1\\2 \ne - 3\,\,\left( {luon\,\,dung} \right)\end{array} \right. \Leftrightarrow m = 2\). Vậy với \(m = 2\) thì hai đường thẳng \(\left( {{d_1}} \right)//\left( {{d_2}} \right)\). 2) Cho phương trình \({x^2} + 4x + 2m + 1 = 0\) (\(m\) là tham số). a) Giải phương trình với \(m = 1\). Với \(m = 1\), phương trình đã cho trở thành: \({x^2} + 4x + 3 = 0\). Nhận xét: \(a - b + c = 1 - 4 + 3 = 0\) nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = - 1\\{x_2} = - \dfrac{c}{a} = - 3\end{array} \right.\). Vậy khi \(m = 1\) thì tập nghiệm của phương trình là \(S = \left\{ { - 1; - 3} \right\}\). b) Tìm \(m\) để phương trình có nghiệm kép. Phương trình \({x^2} + 4x + 2m + 1 = 0\) có \(\Delta ' = {2^2} - \left( {2m + 1} \right) = 4 - 2m - 1 = 3 - 2m\). Để phương trình có nghiệm kép thì \(\Delta = 3 - 2m = 0 \Leftrightarrow m = \dfrac{3}{2}\). Vậy với \(m = \dfrac{3}{2}\) thì phương trình đã cho có nghiệp kép. Câu III (2,0 điểm) Cách giải: 1) Cho tam giác \(ABC\) vuông tại \(A\), có \(AB = 6cm\), góc \(\angle ABC = {60^0}\). Tính chu vi tam giác \(ABC\). Xét tam giác vuông \(ABC\) ta có: \(\begin{array}{l}\tan {60^0} = \dfrac{{AC}}{{AB}} \Rightarrow AC = AB.\tan {60^0} = 6.\sqrt 3 \,\,\left( {cm} \right)\\\cos {60^0} = \dfrac{{AB}}{{BC}} \Rightarrow BC = \dfrac{{AB}}{{\cos {{60}^0}}} = \dfrac{6}{{\dfrac{1}{2}}} = 12\,\,\left( {cm} \right)\end{array}\) Vậy chu vi tam giác \(ABC\) là: \({C_{\Delta ABC}} = AB + AC + BC = 6 + 6\sqrt 3 + 12 = 18 + 6\sqrt 3 \,\,\,\left( {cm} \right)\). 2) Một chiếc ti vi giảm giá hai lần, mỗi lần giảm giá 10% so với giá đang bán, sau khi giảm giá 2 lần thì giá còn lại là 16 200 000 đồng. Hỏi giá ban đầu của chiếc ti vi là bao nhiêu? Gọi giá ban đầu của chiếc ti vi là \(x\) (đồng) (ĐK: \(x > 0\)). Giá của chiếc ti vi sau lần giảm giá 10% đầu tiên là: \(x.90\% = \dfrac{9}{{10}}x\) (đồng). Giá của chiếc ti vi sau lần giảm giá 10% thứ hai là: \(\dfrac{9}{{10}}x.90\% = \dfrac{{81}}{{100}}x\) (đồng). Vì sau khi giảm giá 2 lần thì giá còn lại là 16 200 000 đồng nên ta có phương trình: \(\dfrac{{81}}{{100}}x = 16\,200\,000 \Leftrightarrow x = 20\,000\,000\) (đồng) (tm). Vậy giá ban đầu của chiếc ti vi là 20 000 000 đồng. Câu IV (2,0 điểm) Cách giải: Cho tam giác nhọn \(ABC\) \(\left( {AB \ne AC} \right)\) có các đường cao \(AD,\,\,BE,\,\,CF\) cắt nhau tại H. 1) Chứng minh rằng: Tứ giác \(AEHF\) là tứ giác nội tiếp. Xét tứ giác \(AEHF\) có: \(\left\{ \begin{array}{l}BE \bot AC\\CF \bot AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\angle AEH = {90^0}\\\angle AFH = {90^0}\end{array} \right.\) \( \Rightarrow \angle AEH + \angle AFH = {90^0} + {90^0} = {180^0}\). Vậy \(AEHF\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)). 2) Chứng minh rằng: \(\angle ADE = \angle ADF\). Xét tứ giác \(BDHF\) có: \(\left\{ \begin{array}{l}AD \bot BC\\CF \bot AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\angle BDH = {90^0}\\\angle BFH = {90^0}\end{array} \right.\) \( \Rightarrow \angle BDH + \angle BFH = {90^0} + {90^0} = {180^0}\). \( \Rightarrow BDHF\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)). \( \Rightarrow \angle HDF = \angle HBF\) (hai góc nội tiếp cùng chắn cung \(HF\)) \( \Rightarrow \angle ADF = \angle ABE\) (1). Tương tự xét tứ giác \(CDHE\) có: \(\left\{ \begin{array}{l}AD \bot BC\\BE \bot AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\angle HDC = {90^0}\\\angle HEC = {90^0}\end{array} \right.\). \( \Rightarrow \angle HDC + \angle HEC = {90^0} + {90^0} = {180^0}\). \( \Rightarrow CDHE\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)). \( \Rightarrow \angle HDE = \angle HCE\) (hai góc nội tiếp cùng chắn cung \(HE\)) \( \Rightarrow \angle ADE = \angle ACF\) (2). Ta lại có: \(\angle ABE + \angle BAC = {90^0}\) (do tam giác \(ABE\) vuông tại \(E\)). \(\angle ACF + \angle BAC = {90^0}\) (do tam giác \(ACF\) vuông tại \(F\)). \(\angle ABE = \angle ACF\) (cùng phụ với \(\angle BAC\)) (3). Từ (1), (2), (3) \( \Rightarrow \angle ADE = \angle ADF\) (đpcm). 3) Chứng minh rằng: Đường tròn ngoại tiếp tam giác \(EDF\) đi qua trung điểm \(M\) của cạnh \(BC\). Gọi \(M\) là trung điểm của \(BC\), ta sẽ chứng minh tú giác \(DMEF\) là tứ giác nội tiếp. Xét tam giác \(BEC\) vuông tại \(E\) có trung tuyến \(EM\) ứng với cạnh huyền \(BC\) \( \Rightarrow ME = \dfrac{1}{2}BC = MB = MC\) (định lí đường trung tuyến trong tam giác vuông). \( \Rightarrow \Delta MBE\) cân tại \(M\) \( \Rightarrow \angle MBE = \angle MEB\) (tính chất tam giác cân). \( \Rightarrow \angle EMC = \angle MEB + \angle MBE = 2\angle MBE = 2\angle DBH\,\,\,\left( * \right)\) (góc ngoài của tam giác). Vì \(BDHF\) là tứ giác nội tiếp (cmt) nên \(\angle DBH = \angle DFH\,\,\left( 5 \right)\) (hai góc nội tiếp cùng chắn cung \(DH\)). Vì \(AEHF\) là tứ giác nội tiếp (cmt) nên \(\angle HFE = \angle HAE\,\,\left( 3 \right)\) (hai góc nội tiếp cùng chắn cung \(HE\)). Mà \(\angle DBH + \angle ACB = {90^0}\) (do tam giác \(BCE\) vuông tại \(E\)). \(\angle HAE + \angle ACB = {90^0}\) (do tam giác \(ACD\) vuông tại \(D\)). \( \Rightarrow \angle DBH = \angle HAE\,\,\left( 4 \right)\) (cùng phụ với \(\angle ACB\)). Từ (3) và (4) \( \Rightarrow \angle HFE = \angle DBH\,\,\left( 6 \right)\). Từ (5) và (6) \( \Rightarrow \angle DFE = \angle DFH + \angle HFE = \angle DBH + \angle DBH = 2\angle DBH\,\,\left( {2*} \right)\) Từ (*) và (2*) \( \Rightarrow \angle EMC = \angle DFE\). \( \Rightarrow \) Tứ giác \(DMEF\) là tứ giác nội tiếp (Tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện). Vậy đường tròn ngoại tiếp tam giác \(DEF\) đi qua trung điểm \(M\) của \(BC\) (đpcm). Câu V (2,0 điểm) Cách giải: 1) Tìm các số thực \(x,\,\,y,\,\,z\) thỏa mãn \({x^2} + {y^2} + 4{z^2} - 4x - 2y + 4z + 6 = 0\). Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,\,{x^2} + {y^2} + 4{z^2} - 4x - 2y + 4z + 6 = 0\\ \Leftrightarrow {x^2} - 4x + 4 + {y^2} - 2y + 1 + 4{z^2} + 4z + 1 = 0\\ \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {2z + 1} \right)^2} = 0\end{array}\) Vì \(\left\{ \begin{array}{l}{\left( {x - 2} \right)^2} \ge 0\,\,\forall x\\{\left( {y - 1} \right)^2} \ge 0\,\,\forall y\\{\left( {2z + 1} \right)^2} \ge 0\,\,\forall z\end{array} \right. \Rightarrow {\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {2z + 1} \right)^2} \ge 0\,\,\forall x,\,\,y,\,\,z\). Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 0\\y - 1 = 0\\2z + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\\z = - \dfrac{1}{2}\end{array} \right.\). Vậy có duy nhất 1 bộ số \(\left( {x;y;z} \right)\) thỏa mãn yêu cầu bài toán là \(\left( {x;y;z} \right) = \left( {2;1; - \dfrac{1}{2}} \right)\). 2) Cho các số thực \(x,\,\,y\) thỏa mãn \(x > 2y\) và \(xy = 3\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + 4{y^2} - 11}}{{x - 2y}}\). Ta có: \(\begin{array}{l}P = \dfrac{{{x^2} + 4{y^2} - 11}}{{x - 2y}}\\P = \dfrac{{{x^2} + 4{y^2} - 12 + 1}}{{x - 2y}}\\P = \dfrac{{{x^2} + 4{y^2} - 4xy + 1}}{{x - 2y}}\\P = \dfrac{{{{\left( {x - 2y} \right)}^2} + 1}}{{x - 2y}}\\P = x - 2y + \dfrac{1}{{x - 2y}}\end{array}\) Vì \(x > 2y \Rightarrow x - 2y > 0\). Áp dụng BĐT Cô-si cho hai số \(x - 2y\) và \(\dfrac{1}{{x - 2y}}\) ta có: \(P = x - 2y + \dfrac{1}{{x - 2y}} \ge 2\sqrt {\left( {x - 2y} \right).\dfrac{1}{{x - 2y}}} = 2\). Dấu “=” xảy ra \( \Leftrightarrow x - 2y = \dfrac{1}{{x - 2y}} \Leftrightarrow {\left( {x - 2y} \right)^2} = 1\) \( \Leftrightarrow x - 2y = 1\) (do \(x - 2y > 0\)) và \(xy = 3\). \( \Leftrightarrow \left\{ \begin{array}{l}x - 2y = 1\\xy = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y + 1\\\left( {2y + 1} \right).y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y + 1\\2{y^2} + y - 3 = 0\,\,\left( * \right)\end{array} \right.\). Xét phương trình (*) có \(a + b + c = 2 + 1 - 3 = 0\) nên phương trình (*) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{y_1} = 1\\{y_2} = \dfrac{c}{a} = - \dfrac{3}{2}\end{array} \right.\) Với \({y_1} = 1 \Rightarrow {x_1} = 2{y_1} + 1 = 3\). Với \({y_2} = - \dfrac{3}{2} \Rightarrow {x_2} = 2{y_2} + 1 = - 2\). \( \Rightarrow \) Dấu “=” xảy ra khi và chỉ khi \(\left( {x;y} \right) \in \left\{ {\left( {3;1} \right);\left( { - 2; - \dfrac{3}{2}} \right)} \right\}\). Vậy \({P_{\min }} = 2 \Leftrightarrow \left( {x;y} \right) \in \left\{ {\left( {3;1} \right);\left( { - 2; - \dfrac{3}{2}} \right)} \right\}\).
|





















Danh sách bình luận