Đề thi vào 10 môn Toán Hòa Bình năm 2019Tải vềCâu I (2 điểm): 1) Tính: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
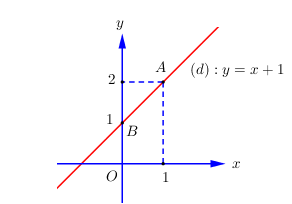
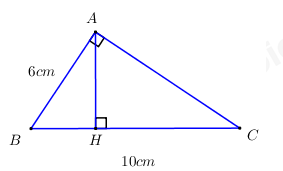
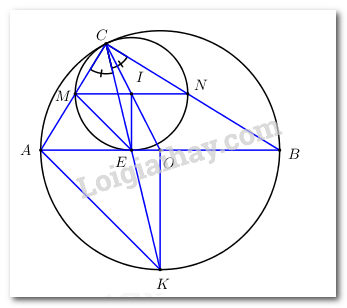
Đề bài Câu I (2 điểm): 1) Tính: a) \(A = 3 + \dfrac{1}{2}\) b) \(B = \sqrt {25} - 1\) 2) Tìm \(x\) biết: a) \(x + 2 = 9\) b) \(\sqrt {x + 1} = 3\) Câu II (2 điểm): 1) Giải phương trình \({x^2} - 7x + 12 = 0\). 2) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = - 1\\4x + y = 3\end{array} \right.\) Câu III (3 điểm): 1) Tìm giá trị \(m\) để đường thẳng \(\left( d \right):\,\,y = x + m\) đi qua điểm \(A\left( {1;2} \right)\). Khi đó hãy vẽ đường thẳng \(\left( d \right)\) trong hệ trục tọa độ \(Oxy\). 2) Cho tam giác \(ABC\) vuông tại \(A\), có đường cao \(AH\). Biết \(AB = 6cm,\,\,BC = 10cm\), tính độ dài \(AH\) và diện tích tam giác \(ABC\). 3) Một người đi xe máy từ A đến B với thời gian và vận tốc đã dự định. Nếu người đó đi nhanh hơn dự định trong mỗi giờ là 10km thì đến đích sớm hơn dự định là 36 phút. Nếu người đó đi chậm hơi dự định trong mỗi giờ là 10km thì đến đích muộn hơn dự định là 1 giờ. Tính vận tốc dự định của người đó và chiều dài quãng đường AB. Câu IV (2 điểm): Cho đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là một điểm nằm trên \(\left( O \right)\) (C khác A, B). Đường phân giác của góc \(ACB\) cắt đoạn thẳng \(AB\) tại \(E\) và cắt \(\left( O \right)\) tại điểm thứ hai là \(K\). 1) Chứng minh rằng tam giác \(KAE\) đồng dạng với tam giác \(KCA\). 2) Cho đường tròn \(\left( I \right)\) đi qua điểm \(E\) và tiếp xúc với đường tròn \(\left( O \right)\) tại tiếp điểm \(C\), đường tròn \(\left( I \right)\) cắt \(CA,\,\,CB\) tại điểm thứ hai theo thứ tự là \(M,\,\,N\). Chứng minh rằng \(MN\) song song với \(AB\). Câu V (1 điểm): Giải phương trình \({x^2} + \dfrac{{{x^2}}}{{{{\left( {x + 1} \right)}^2}}} = 1\). Lời giải Câu I (VD): Phương pháp: 1a) Quy đồng. 1b) Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\). 2a) Chuyển vế tìm \(x\). 2b) Tìm ĐKXĐ. \(\sqrt A = B\,\,\left( {B \ge 0} \right) \Leftrightarrow A = {B^2}\). Cách giải: 1a) \(A = 3 + \dfrac{1}{2} = \dfrac{{6 + 1}}{2} = \dfrac{7}{2}\). Vậy \(A = \dfrac{7}{2}\). 1b) \(B = \sqrt {25} - 1 = \sqrt {{5^2}} - 1 = 5 - 1 = 4\). Vậy \(B = 4\). 2a) \(x + 2 = 9 \Leftrightarrow x = 9 - 2 \Leftrightarrow x = 7\). Vậy \(x = 7\). 2b) ĐKXĐ: \(x + 1 \ge 0 \Leftrightarrow x \ge - 1\). \(\sqrt {x + 1} = 3 \Leftrightarrow x + 1 = 9 \Leftrightarrow x = 9 - 1 \Leftrightarrow x = 8\,\,\left( {tm} \right)\). Vậy \(x = 8\). Câu II (VD) Phương pháp: 1) Giải phương trình bằng cách đưa về dạng tích hoặc sử dụng biệt thức \(\Delta \). 2) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số. Cách giải: 1) Giải phương trình \({x^2} - 7x + 12 = 0\). \(\begin{array}{l}{x^2} - 7x + 12 = 0 \Leftrightarrow {x^2} - 3x - 4x + 12 = 0\\ \Leftrightarrow x\left( {x - 3} \right) - 4\left( {x - 3} \right) = 0 \Leftrightarrow \left( {x - 3} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 4\end{array} \right.\end{array}\) Vậy tập nghiệm của phương trình là \(S = \left\{ {3;4} \right\}\). 2) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = - 1\\4x + y = 3\end{array} \right.\) \(\left\{ \begin{array}{l}2x + 3y = - 1\\4x + y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 6y = - 2\\4x + y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y = - 5\\2x + 3y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - 1\\2x - 3 = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 2\\y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right.\) Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {1; - 1} \right)\). Câu III (VD): Phương pháp: 1) Thay tọa độ điểm \(A\) vào phương trình đường thẳng \(d\) tìm \(m\), xác định hai điểm mà đường thẳng \(d\) đi qua và vẽ đường thẳng \(d\) trong hệ trục tọa độ \(Oxy\). 2) Áp dụng định lí Pytago và các hệ thức lượng trong tam giác vuông. 3) - Gọi vận tốc dự định và thời gian dự định đi hết quãng đường AB lần lượt là \(x\,\,\left( {km/h} \right)\) và \(y\,\,\left( h \right)\) (ĐK: \(x,y > 0\)). - Từ mối liên hệ: Quãng đường = Vận tốc \( \times \) Thời gian, lập 2 phương trình liên quan đến \(x;y\). - Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số và kết luận. Cách giải: 1) \(A\left( {1;2} \right) \in \left( d \right):\,\,y = x + m\) nên thay tọa độ điểm \(A\) vào phương trình đường thẳng \(\left( d \right)\) ta có: \(2 = 1 + m \Leftrightarrow m = 2 - 1 \Leftrightarrow m = 1\). Khi đó, phương trình đường thẳng \(\left( d \right)\) là \(y = x + 1\). Cho \(x = 0 \Rightarrow y = 1 \Rightarrow \left( d \right)\) đi qua điểm \(B\left( {0;1} \right)\). Vẽ đường thẳng \(\left( d \right)\). 2) Cho tam giác \(ABC\) vuông tại \(A\), có đường cao \(AH\). Biết \(AB = 6cm,\,\,BC = 10cm\), tính độ dài \(AH\) và diện tích tam giác \(ABC\). Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có: \(\begin{array}{l}A{B^2} + A{C^2} = B{C^2} \Leftrightarrow {6^2} + A{C^2} = {10^2}\\ \Leftrightarrow A{C^2} = {10^2} - {6^2} = 64 \Leftrightarrow AC = 8\,\,\left( {cm} \right)\end{array}\) Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có: \(AH.BC = AB.AC \Leftrightarrow AH.10 = 6.8 \Leftrightarrow AH = \dfrac{{48}}{{10}} = 4,8\,\,\left( {cm} \right)\). Diện tích tam giác vuông \(ABC\) là \({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.6.8 = 24\,\,\left( {c{m^2}} \right)\). 3) Một người đi xe máy từ A đến B với thời gian và vận tốc đã dự định. Nếu người đó đi nhanh hơn dự định trong mỗi giờ là 10km thì đến đích sớm hơn dự định là 36 phút. Nếu người đó đi chậm hơi dự định trong mỗi giờ là 10km thì đến đích muộn hơn dự định là 1 giờ. Tính vận tốc dự định của người đó và chiều dài quãng đường AB. Gọi vận tốc dự định và thời gian dự định đi hết quãng đường AB lần lượt là \(x\,\,\left( {km/h} \right)\) và \(y\,\,\left( h \right)\) (ĐK: \(x,y > 0\)). Khi đó độ dài quãng đường AB là \(xy\,\,\left( {km} \right)\). +) Nếu người đó đi nhanh hơn dự định trong mỗi giờ là 10km, tức là đi với vận tốc \(x + 10\,\,\left( {km/h} \right)\) thì người đó đến đích sớm hơn dự định 36 phút = \(\dfrac{{36}}{{60}} = \dfrac{3}{5}\,\,\left( h \right)\), tức là đi hết quãng đường trong \(y - \dfrac{3}{5}\,\,\left( h \right)\). Khi đó độ dài quãng đường AB là \(\left( {x + 10} \right)\left( {y - \dfrac{3}{5}} \right) = xy\). \( \Leftrightarrow xy - \dfrac{3}{5}x + 10y - 6 = xy \Leftrightarrow - \dfrac{3}{5}x + 10y - 6 = 0 \Leftrightarrow - 3x + 50y - 30 = 0\,\,\left( 1 \right)\) +) Nếu người đó đi chậm hơn dự định trong mỗi giờ là 10km, tức là đi với vận tốc \(x - 10\,\,\left( {km/h} \right)\) thì người đó đến đích muộn hơn dự định \(1\,\,\left( h \right)\), tức là đi hết quãng đường trong \(y + 1\,\,\left( h \right)\). Khi đó độ dài quãng đường AB là \(\left( {x - 10} \right)\left( {y + 1} \right) = xy\). \( \Leftrightarrow xy + x - 10y - 10 = xy \Leftrightarrow x - 10y - 10 = 0\,\,\left( 2 \right)\) Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l} - 3x + 50y - 30 = 0\\x - 10y - 10 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 50y = - 30\\3x - 30y = 30\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 20y = - 60\\x - 10y - 10 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\,\,\left( {tm} \right)\\x - 30 - 10 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 40\\y = 3\end{array} \right.\,\,\left( {tm} \right)\). Vậy vận tốc dự định và thời gian dự định đi hết quãng đường AB lần lượt là \(40\,\,km/h\) và \(3h\), độ dài quãng đường AB là \(xy = 40.3 = 120\,\,\left( {km} \right)\). Câu IV (VD): Phương pháp: 1) Chứng minh rằng tam giác \(KAE\) đồng dạng với tam giác \(KCA\) theo trường hợp góc – góc. 2) Xác định điểm I. Chứng minh \(\left\{ \begin{array}{l}IE\parallel OK\\IE \bot MN\\OK \bot AB\end{array} \right.\), từ đó suy ra \(MN\parallel AB\). Cách giải: 1) Chứng minh rằng tam giác \(KAE\) đồng dạng với tam giác \(KCA\). Ta có \(\angle KAB = \angle KCB\) (hai góc nội tiếp cùng chắn cung \(BK\)), lại có \(\angle KCB = \angle KCA\,\,\left( {gt} \right)\). \( \Rightarrow \angle KAB = \angle KCA\) hay \(\angle KAE = \angle KCA\). Xét tam giác \(KAE\) và tam giác \(KCA\) có: 2) Cho đường tròn \(\left( I \right)\) đi qua điểm \(E\) và tiếp xúc với đường tròn \(\left( O \right)\) tại tiếp điểm \(C\), đường tròn \(\left( I \right)\) cắt \(CA,\,\,CB\) tại điểm thứ hai theo thứ tự là \(M,\,\,N\). Chứng minh rằng \(MN\) song song với \(AB\). * Xác định điểm \(I\). Do \(\left( I \right)\) và \(\left( O \right)\) tiếp xúc tại \(C \Rightarrow I,\,\,O,\,\,C\) thẳng hàng \( \Rightarrow I \in OC\). Lại có \(\left( I \right)\) đi qua \(C,\,\,E \Rightarrow IC = IE \Rightarrow I\) thuộc trung trực của \(CE\). Do đó \(I\) là giao điểm của \(OC\) và đường trung trực của \(CE\). * Chứng minh \(MN\parallel AB\). Nối \(OK\) ta có: \(\Delta OCK\) cân tại \(O\,\,\left( {OC = OK} \right) \Rightarrow \angle OCK = \angle OKC\). \(\Delta ICE\) cân tại \(I\,\,\left( {IC = IE} \right) \Rightarrow \angle ICE = \angle IEC\) hay \(\angle OCK = \angle IEC\). \( \Rightarrow \angle OKC = \angle IEC\). Mà 2 góc này ở vị trí hai góc đồng vị bằng nhau \( \Rightarrow IE\parallel OK\) (1). Xét đường tròn \(\left( O \right)\): \(\angle ACK = \angle BCK\,\,\left( {gt} \right) \Rightarrow sdcung\,\,AK = \,\,sdcung\,\,BK\) (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau) \( \Rightarrow K\) là điểm chính giữa cung \(AB\) của \(\left( O \right) \Rightarrow OK \bot AB\) (2). Xét đường tròn \(\left( I \right)\) ta có \(\angle MCN = {90^0} \Rightarrow \angle MCN\) là góc nội tiếp chắn nửa đường tròn) \( \Rightarrow MN\) là đường kính của \(\left( I \right)\). Ta có: \(\angle ACK = \angle BCK \Rightarrow \angle MCE = \angle NCE \Rightarrow sdcung\,\,ME = \,\,sdcung\,\,NE\) (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau) \( \Rightarrow E\) là điểm chính giữa cung \(MN\) của \(\left( O \right) \Rightarrow IE \bot MN\) (3). Từ (1), (2) và (3) ta suy ra được \(MN\parallel AB\) (đpcm). Câu V (VDC) : Phương pháp: Biến đổi \({x^2} + \dfrac{{{x^2}}}{{{{\left( {x + 1} \right)}^2}}}{\left( {\dfrac{{{x^2}}}{{x + 1}}} \right)^2} + \dfrac{{2{x^2}}}{{x + 1}}\) sau đó đặt ẩn phụ \(\dfrac{{{x^2}}}{{x + 1}} = t\). Cách giải: ĐK: \(x \ne - 1\). Ta có: \({x^2} + \dfrac{{{x^2}}}{{{{\left( {x + 1} \right)}^2}}} = {\left( {x - \dfrac{x}{{x + 1}}} \right)^2} + 2\dfrac{{{x^2}}}{{x + 1}} = {\left( {\dfrac{{{x^2}}}{{x + 1}}} \right)^2} + \dfrac{{2{x^2}}}{{x + 1}}\). Khi đó phương trình trở thành \({\left( {\dfrac{{{x^2}}}{{x + 1}}} \right)^2} + \dfrac{{2{x^2}}}{{x + 1}} = 1\). Đặt \(\dfrac{{{x^2}}}{{x + 1}} = t\) ta có phương trình \({t^2} + 2t = 1 \Leftrightarrow {t^2} + 2t - 1 = 0\,\,\left( * \right)\). \({\Delta _t}' = {1^2} + 1 = 2 > 0 \Rightarrow \left( * \right)\) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{t_1} = - 1 + \sqrt 2 \\{t_2} = - 1 - \sqrt 2 \end{array} \right.\). Với \({t_1} = - 1 + \sqrt 2 \) ta có: \(\dfrac{{{x^2}}}{{x + 1}} = - 1 + \sqrt 2 \Leftrightarrow {x^2} + \left( {1 - \sqrt 2 } \right)x + 1 - \sqrt 2 = 0\). \(\Delta = {\left( {1 - \sqrt 2 } \right)^2} - 4\left( {1 - \sqrt 2 } \right) = 2\sqrt 2 - 1 > 0 \Rightarrow \) Phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{\sqrt 2 - 1 + \sqrt {2\sqrt 2 - 1} }}{2}\\{x_2} = \dfrac{{\sqrt 2 - 1 - \sqrt {2\sqrt 2 - 1} }}{2}\end{array} \right.\) Với \({t_1} = - 1 - \sqrt 2 \) ta có: \(\dfrac{{{x^2}}}{{x + 1}} = - 1 - \sqrt 2 \Leftrightarrow {x^2} + \left( {\sqrt 2 + 1} \right)x + \sqrt 2 + 1 = 0\). \(\Delta = {\left( {\sqrt 2 + 1} \right)^2} - 4\left( {\sqrt 2 + 1} \right) = - 1 - 2\sqrt 2 < 0 \Rightarrow \) Phương trình vô nghiệm. Vậy phương trình ban đầu có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{\sqrt 2 - 1 + \sqrt {2\sqrt 2 - 1} }}{2}\\{x_2} = \dfrac{{\sqrt 2 - 1 - \sqrt {2\sqrt 2 - 1} }}{2}\end{array} \right.\).
|














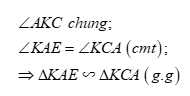






Danh sách bình luận