Đề thi vào 10 môn Toán Thái Bình năm 2020Tải vềCâu 1: Cho Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
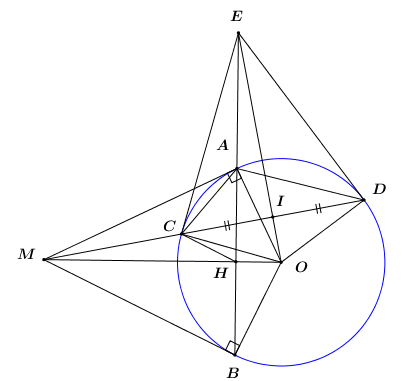
Đề bài Câu 1: Cho \(A = \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}}\) và \(B = \left( {\dfrac{{\sqrt x + 1}}{{\sqrt x - 1}} - \dfrac{{\sqrt x - 1}}{{\sqrt x + 1}}} \right):\dfrac{{\sqrt x }}{{\sqrt x - 1}}\) (với \(x > 0,\,\,x \ne 1\)). a) Tính giá trị của biểu thức A khi \(x = 9\). b) Rút gọn biểu thức B. c) Tìm \(x\) để giá trị của A và B trái dấu. Câu 2: Cho hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 4m - 5\\2x + y = 3m\end{array} \right.\) với \(m\) là tham số. a) Giải hệ phương trình khi \(m = 3.\) b) Tìm \(m\) để hệ phương trình có nghiệm \(\left( {x;\,\,y} \right)\) thỏa mãn \(\dfrac{2}{x} - \dfrac{1}{y} = - 1.\) Câu 3: Cho parabol \(\left( P \right):\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,y = 3mx + 1 - {m^2}\) (\(m\) là tham số). a) Tìm \(m\) để đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {1; - 9} \right).\) b) Tìm \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1};\,\,{x_2}\) thỏa mãn \({x_1} + {x_2} = 2{x_1}{x_2}.\) Câu 4: Qua điểm M nằm bên ngoài đường tròn \(\left( {O;R} \right)\), kẻ hai tiếp tuyến \(MA,\,\,MB\) (\(A,\,\,B\) là hai tiếp điểm). Vẽ cát tuyến \(MCD\) không đi qua tâm \(O\) (\(C\) nằm giữa \(M\) và \(D\)). a) Chứng minh tứ giác \(MAOB\) nội tiếp và \(MO \bot AB\). b) Chứng minh \(MA.AD = MD.AC\). c) Gọi \(I\) là trung điểm của dây cung \(CD\) và \(E\) là giao điểm của hai đường thẳng \(AB\) và \(OI\). Tính độ dài đoan thẳng \(OE\) theo \(R\) khi \(OI = \dfrac{R}{3}\). d) Qua tâm \(O\) kẻ đường thẳng vuông góc với \(OM\) cắt đường thẳng \(MA,\,\,MB\) lần lượt tại \(P\) và \(Q\). Tìm vị trí điểm \(M\) để diện tích tam giác \(MPQ\) đạt giá trị nhỏ nhất. Câu 5: Tìm giá trị lớn nhất của biểu thức \(P = - 3{x^2} - 4x\sqrt y + 16x - 2y + 12\sqrt y + 1998.\) Lời giải chi tiết Câu 1 (2,0 điểm) Cách giải: Cho \(A = \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}}\) và \(B = \left( {\dfrac{{\sqrt x + 1}}{{\sqrt x - 1}} - \dfrac{{\sqrt x - 1}}{{\sqrt x + 1}}} \right):\dfrac{{\sqrt x }}{{\sqrt x - 1}}\) (với \(x > 0,\,\,x \ne 1\)). a) Tính giá trị của biểu thức A khi \(x = 9\). Thay \(x = 9\,\,\left( {TMDK} \right)\) vào biểu thức A ta có: \(A = \dfrac{{\sqrt 9 + 1}}{{\sqrt 9 - 1}} = \dfrac{{3 + 1}}{{3 - 1}} = \dfrac{4}{2} = 2\). Vậy khi \(x = 9\) thì \(A = 2\). b) Rút gọn biểu thức B. Với \(x > 0,\,\,x \ne 1\) thì: \(\begin{array}{l}B = \left( {\dfrac{{\sqrt x + 1}}{{\sqrt x - 1}} - \dfrac{{\sqrt x - 1}}{{\sqrt x + 1}}} \right):\dfrac{{\sqrt x }}{{\sqrt x - 1}}\\B = \dfrac{{{{\left( {\sqrt x + 1} \right)}^2} - {{\left( {\sqrt x - 1} \right)}^2}}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}:\dfrac{{\sqrt x }}{{\sqrt x - 1}}\\B = \dfrac{{x + 2\sqrt x + 1 - x + 2\sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}:\dfrac{{\sqrt x }}{{\sqrt x - 1}}\\B = \dfrac{{4\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}.\dfrac{{\sqrt x - 1}}{{\sqrt x }}\\B = \dfrac{4}{{\sqrt x + 1}}\end{array}\) Vậy với \(x > 0,\,\,x \ne 1\) thì \(B = \dfrac{4}{{\sqrt x + 1}}\). c) Tìm \(x\) để giá trị của A và B trái dấu. Để giá trị của A và B trái dấu thì \(A.B < 0\). \(\begin{array}{l} \Rightarrow \dfrac{{\sqrt x + 1}}{{\sqrt x - 1}}.\dfrac{4}{{\sqrt x + 1}} < 0\\ \Leftrightarrow \dfrac{4}{{\sqrt x - 1}} < 0\end{array}\) Vì \(4 > 0\) nên \(\dfrac{4}{{\sqrt x - 1}} < 0 \Leftrightarrow \sqrt x - 1 < 0 \Leftrightarrow \sqrt x < 1 \Leftrightarrow x < 1\). Kết hợp điều kiện \(x > 0,\,\,x \ne 1\) ta có \(0 < x < 1\). Vậy để giá trị của A và B trái dấu thì \(0 < x < 1\). Câu 2 (2 điểm) Cách giải: Cho hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 4m - 5\\2x + y = 3m\end{array} \right.\) với \(m\) là tham số. a) Giải hệ phương trình khi \(m = 3.\) Với \(m = 3\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 7\\2x + y = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2y = 7\\4x + 2y = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 25\\y = 9 - 2x\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 9 - 2.5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = - 1\end{array} \right.\) Vậy với \(m = 3\) thì hệ phương trình có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( {5; - 1} \right).\) b) Tìm \(m\) để hệ phương trình có nghiệm \(\left( {x;\,\,y} \right)\) thỏa mãn \(\dfrac{2}{x} - \dfrac{1}{y} = - 1.\) Ta có: \(\left\{ \begin{array}{l}x - 2y = 4m - 5\,\,\,\,\,\,\left( 1 \right)\\2x + y = 3m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\) Từ phương trình \(\left( 2 \right)\) ta có: \(y = 3m - 2x\) Thế vào phương trình \(\left( 1 \right)\) ta có: \(\begin{array}{l}\left( 1 \right) \Leftrightarrow x - 2\left( {3m - 2x} \right) = 4m - 5\\ \Leftrightarrow x - 6m + 4x = 4m - 5\\ \Leftrightarrow 5x = 10m - 5\\ \Leftrightarrow x = 2m - 1\\ \Rightarrow y = 3m - 2x\\ \Leftrightarrow y = 3m - 2\left( {2m - 1} \right)\\ \Leftrightarrow y = 3m - 4m + 2\\ \Leftrightarrow y = - m + 2\end{array}\) \( \Rightarrow \) Với mọi \(m\) thì hệ phương trình luôn có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( {2m - 1;\,\, - m + 2} \right).\) Theo đề bài ta có: \(\dfrac{2}{x} - \dfrac{1}{y} = - 1\,\,\,\left( * \right)\) Điều kiện: \(\left\{ \begin{array}{l}x \ne 0\\y \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2m - 1 \ne 0\\ - m + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne \dfrac{1}{2}\\m \ne 2\end{array} \right..\) \(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow \dfrac{2}{{2m - 1}} - \dfrac{1}{{ - m + 2}} = - 1\\ \Leftrightarrow \dfrac{2}{{2m - 1}} + \dfrac{1}{{m - 2}} + 1 = 0\\ \Rightarrow \left( {2m - 1} \right)\left( {m - 2} \right) + 2\left( {m - 2} \right) + 2m - 1 = 0\\ \Leftrightarrow 2{m^2} - 5m + 2 + 2m - 4 + 2m - 1 = 0\\ \Leftrightarrow 2{m^2} - m - 3 = 0\\ \Leftrightarrow 2{m^2} + 2m - 3m - 3 = 0\\ \Leftrightarrow 2m\left( {m + 1} \right) - 3\left( {m + 1} \right) = 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {2m - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\2m - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 1\,\,\,\left( {tm} \right)\\m = \dfrac{3}{2}\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy \(m = - 1\) và \(m = \dfrac{3}{2}\) thỏa mãn điều kiện bài toán. Câu 3 (2 điểm) Cách giải: Cho parabol \(\left( P \right):\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,\,y = 3mx + 1 - {m^2}\) (\(m\) là tham số). a) Tìm \(m\) để đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {1; - 9} \right).\) Đường thẳng \(\left( d \right):\,\,\,y = 3mx + 1 - {m^2}\) đi qua điểm \(A\left( {1; - 9} \right)\) \(\begin{array}{l} \Rightarrow - 9 = 3m.1 + 1 - {m^2}\\ \Leftrightarrow {m^2} - 3m - 9 - 1 = 0\\ \Leftrightarrow {m^2} - 3m - 10 = 0\end{array}\) Phương trình có \(\Delta = {\left( { - 3} \right)^2} + 4.10 = 49 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{m_1} = \dfrac{{3 + \sqrt {49} }}{2} = 5\\{m_2} = \dfrac{{3 - \sqrt {49} }}{2} = - 2\end{array} \right..\) Vậy \(m = - 2\) hoặc \(m = 5\) thỏa mãn bài toán. b) Tìm \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1};\,\,{x_2}\) thỏa mãn \({x_1} + {x_2} = 2{x_1}{x_2}.\) Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là: \({x^2} = 3mx + 1 - {m^2} \Leftrightarrow {x^2} - 3mx + {m^2} - 1 = 0\,\,\,\,\left( * \right)\) Đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ giao điểm là \({x_1},\,\,{x_2}\) \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) \(\begin{array}{l} \Leftrightarrow \Delta > 0\\ \Leftrightarrow {\left( {3m} \right)^2} - 4\left( {{m^2} - 1} \right) > 0\\ \Leftrightarrow 9{m^2} - 4{m^2} + 4 > 0\\ \Leftrightarrow 5{m^2} + 4 > 0\,\,\,\forall m\end{array}\) \( \Rightarrow \) Với mọi \(m\) thì \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ là \({x_1},\,{x_2}.\) Áp dụng hệ thức Vi-et với phương trình \(\left( * \right)\) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3m\\{x_1}{x_2} = {m^2} - 1\end{array} \right..\) Theo đề bài ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\,\,{x_1} + {x_2} = 2{x_1}{x_2}\\ \Leftrightarrow 3m = 2\left( {{m^2} - 1} \right)\\ \Leftrightarrow 2{m^2} - 2 - 3m = 0\\ \Leftrightarrow 2{m^2} - 3m - 2 = 0\end{array}\) Phương trình có \(\Delta = {\left( { - 3} \right)^2} + 4.2.2 = 25 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{m_1} = \dfrac{{3 + \sqrt {25} }}{{2.2}} = 2\\{m_2} = \dfrac{{3 - \sqrt {25} }}{{2.2}} = - \dfrac{1}{2}\end{array} \right..\) Vậy \(m = - \dfrac{1}{2}\) và \(m = 2\) thỏa mãn yêu cầu bài toán. Câu 4 (3,5 điểm) Cách giải: Qua điểm M nằm bên ngoài đường tròn \(\left( {O;R} \right)\), kẻ hai tiếp tuyến \(MA,\,\,MB\) (\(A,\,\,B\) là hai tiếp điểm). Vẽ cát tuyến \(MCD\) không đi qua tâm \(O\) (\(C\) nằm giữa \(M\) và \(D\)). a) Chứng minh tứ giác \(MAOB\) nội tiếp và \(MO \bot AB\). Vì \(MA,\,\,MB\) là các tiếp tuyến của \(\left( O \right)\) nên \(\angle OAM = \angle OBM = {90^0}\). Xét tứ giác \(MAOB\) có: \(\angle OAM + \angle OBM = {90^0} + {90^0} = {180^{}}\). \( \Rightarrow MAOB\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)). Vì \(OA = OB\) \(\left( { = R} \right)\) \( \Rightarrow O\) thuộc trung trực của \(AB\). \(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của \(AB\). \( \Rightarrow MO\) là trung trực của đoạn thẳng \(AB\). Vậy \(MO \bot AB\) (đpcm). b) Chứng minh \(MA.AD = MD.AC\). Xét \(\Delta MAC\) và \(\Delta MDA\) có: \(\angle AMD\) chung; \(\angle MAC = \angle MDA\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AC\)). \( \Rightarrow \Delta MAC \sim \Delta MDA\,\,\left( {g.g} \right)\) \( \Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{AC}}{{AD}}\) (hai cạnh tương ứng) \( \Rightarrow MA.AD = MD.AC\,\,\left( {dpcm} \right)\). c) Gọi \(I\) là trung điểm của dây cung \(CD\) và \(E\) là giao điểm của hai đường thẳng \(AB\) và \(OI\). Tính độ dài đoan thẳng \(OE\) theo \(R\) khi \(OI = \dfrac{R}{3}\). Gọi \(AB \cap OM = \left\{ H \right\}\), theo ý a) ta có \(OM \bot AB\) tại \(H\). Áp dụng hệ thức lượng trong tam giác vuông \(OAM\), đường cao \(AH\) ta có: \(O{A^2} = OH.OM\). Mà \(OA = OC\,\,\left( { = R} \right)\) nên \(O{C^2} = OH.OM \Rightarrow \dfrac{{OC}}{{OH}} = \dfrac{{OM}}{{OC}}\). Xét \(\Delta OCH\) và \(\Delta OMC\) có: \(\angle COM\) chung; \(\dfrac{{OC}}{{OH}} = \dfrac{{OM}}{{OC}}\) (cmt). \( \Rightarrow \Delta OCH \sim \Delta OMC\,\,\left( {c.g.c} \right)\) \( \Rightarrow \angle OCH = \angle OMC = \angle OMI\,\,\left( 1 \right)\) (hai góc tương ứng). Vì \(I\) là trung điểm của \(CD\,\,\left( {gt} \right)\) nên \(OI \bot CD\) (quan hệ vuông góc giữa đường kính và dây cung). \( \Rightarrow \Delta OMI\) vuông tại \(I\) \( \Rightarrow \angle OMI + \angle MOI = {90^0}\). Lại có: \(\angle OEH + \angle EOH = {90^0}\) (do tam giác \(OEH\) vuông tại \(H\)). Mà \(\angle MOI = \angle EOH\) nên \(\angle OMI = \angle OEH\,\,\,\left( 2 \right)\). Từ (1) và (2) \( \Rightarrow \angle OCH = \angle OEH\) \(\left( { = \angle OMI} \right)\). \( \Rightarrow \) Tứ giác \(OECH\) là tứ giác nội tiếp (Tứ giác có 2 góc kề cùng nhìn 1 cạnh dưới các goác bằng nhau). \( \Rightarrow \angle OCE = \angle OHE = {90^0}\) (2 góc nội tiếp cùng chắn cung \(OE\)). \( \Rightarrow \Delta OCE\) vuông tại \(C\), có đường cao \(CI\). Áp dụng hệ thức lượng trong tam giác vuông \(OCE\) ta có: \(O{C^2} = OI.OE \Rightarrow OE = \dfrac{{O{C^2}}}{{OI}} = \dfrac{{{R^2}}}{{\dfrac{R}{3}}} = 3R\). Vậy khi \(OI = \dfrac{R}{3}\) thì \(OE = 3R\). d) Qua tâm \(O\) kẻ đường thẳng vuông góc với \(OM\) cắt đường thẳng \(MA,\,\,MB\) lần lượt tại \(P\) và \(Q\). Tìm vị trí điểm \(M\) để diện tích tam giác \(MPQ\) đạt giá trị nhỏ nhất. Đặt \(OM = x\,\,\left( {x > R} \right)\). Áp dụng hệ thức lượng trong tam giác vuông \(OMP\), đường cao \(OA\) ta có: \(\begin{array}{l}\dfrac{1}{{O{A^2}}} = \dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{P^2}}}\\ \Rightarrow \dfrac{1}{{{R^2}}} = \dfrac{1}{{{x^2}}} + \dfrac{1}{{O{P^2}}}\\ \Rightarrow \dfrac{1}{{O{P^2}}} = \dfrac{1}{{{R^2}}} - \dfrac{1}{{{x^2}}} = \dfrac{{{x^2} - {R^2}}}{{{x^2}{R^2}}}\\ \Rightarrow OP = \dfrac{{xR}}{{\sqrt {{x^2} - {R^2}} }}\end{array}\) Xét tam giác \(MPQ\) có đường cao \(MO\) đồng thời là đường phân giác (Tính chất 2 tiếp tuyến cắt nhau) nên \(\Delta MPQ\) là tam giác cân tại \(M\), do đó đường cao \(MO\) cũng đồng thời là đường trung tuyến. \( \Rightarrow PQ = 2OP = \dfrac{{2xR}}{{\sqrt {{x^2} - {R^2}} }}\). Khi đó \({S_{\Delta MPQ}} = \dfrac{1}{2}MO.PQ = \dfrac{1}{2}.x.\dfrac{{2xR}}{{\sqrt {{x^2} - {R^2}} }} = R.\dfrac{{{x^2}}}{{\sqrt {{x^2} - {R^2}} }}\). Ta có: \(\dfrac{{{x^2}}}{{\sqrt {{x^2} - {R^2}} }} = \dfrac{{{x^2} - {R^2} + {R^2}}}{{\sqrt {{x^2} - {R^2}} }} = \sqrt {{x^2} - {R^2}} + \dfrac{{{R^2}}}{{\sqrt {{x^2} - {R^2}} }}\). Áp dụng BĐT Cô-si cho 2 số dương \(\sqrt {{x^2} - {R^2}} \) và \(\dfrac{{{R^2}}}{{\sqrt {{x^2} - {R^2}} }}\) ta có: \(\sqrt {{x^2} - {R^2}} + \dfrac{{{R^2}}}{{\sqrt {{x^2} - {R^2}} }} \ge 2\sqrt {\sqrt {{x^2} - {R^2}} .\dfrac{{{R^2}}}{{\sqrt {{x^2} - {R^2}} }}} = 2R\). Khi đó \({S_{\Delta MPQ}} \ge R.2R = 2{R^2}\). Dấu “=” xảy ra \( \Leftrightarrow \sqrt {{x^2} - {R^2}} = \dfrac{{{R^2}}}{{\sqrt {{x^2} - {R^2}} }}\) \( \Leftrightarrow {x^2} - {R^2} = {R^2} \Leftrightarrow {x^2} = 2{R^2} \Leftrightarrow x = R\sqrt 2 \,\,\left( {tm} \right)\). Vậy diện tích tam giác \(MPQ\) đạt giá trị nhỏ nhất bằng \(2{R^2}\) khi và chỉ khi \(M\) cách tâm \(O\) một khoảng bằng \(R\sqrt 2 \). Câu 5 (0,5 điểm) Cách giải: Tìm giá trị lớn nhất của biểu thức \(P = - 3{x^2} - 4x\sqrt y + 16x - 2y + 12\sqrt y + 1998.\) Điều kiện: \(y \ge 0.\) \(\begin{array}{l}P = - 3{x^2} - 4x\sqrt y + 16x - 2y + 12\sqrt y + 1998\\\,\,\,\,\, = \left( { - 2{x^2} - 4x\sqrt y - 2y + 12x + 12\sqrt y } \right) - {x^2} + 4x + 1998\\\,\,\,\,\, = - 2\left( {{x^2} + 2x\sqrt y + y - 6x - 6\sqrt y + 9} \right) - \left( {{x^2} - 4x + 4} \right) + 18 + 4 + 1998\\\,\,\,\,\, = - 2{\left( {x + \sqrt y - 3} \right)^2} - {\left( {x - 2} \right)^2} + 2020\end{array}\) Vì \(\left\{ \begin{array}{l} - 2{\left( {x + \sqrt y - 3} \right)^2} \le 0\,\,\,\forall x,\,\,y \ge 0\\ - {\left( {x - 2} \right)^2} \le 0\,\,\,\forall x\end{array} \right.\) \( \Rightarrow P \le 2020\,\,\forall x,\,\,y \ge 0\) Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x + \sqrt y - 3 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\\sqrt y = 3 - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\,\,\,\left( {tm} \right)\end{array} \right.\) Vậy \(Max\,\,P = 2020\) khi \(x = 2\) và \(y = 1.\)
|




















Danh sách bình luận