Đề thi vào 10 môn Toán Quảng Ninh năm 2021Tải vềCâu 1 (2,0 điểm): a) Thực hiện phép tính: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
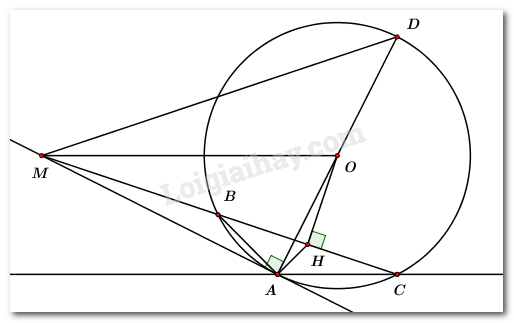
Đề bài Câu 1 (2,0 điểm): a) Thực hiện phép tính: \(2\sqrt {16} - \sqrt {25} .\) b) Rút gọn biểu thức: \(A = \left( {\dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}} \right):\dfrac{{\sqrt x }}{{x - 4}}\) với \(x > 0,\,\,x \ne 4.\) c) Giải hệ phương trình: \(\left\{ \begin{array}{l}x + 4y = 9\\x + 3y = 7\end{array} \right..\) Bài 2 (2,0 điểm): Cho phương trình \({x^2} - 2x + m - 1 = 0\,\,\), với \(m\) là tham số. a) Giải phương trình với \(m = - 2\). b) Tìm các giá trị của tham số \(m\) để phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1}^2 + {x_2}^2 - 3{x_1}{x_2} = 2{m^2} + \left| {m - 3} \right|\). Câu 3 (2 điểm): Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình. Lớp 9B có 42 học sinh. Vừa qua lớp đã phát động phong trào tặng sách cho các bạn đang cách ly vì dịch bệnh Covid-19. Tại buổi phát động, mỗi học sinh trong lớp đều tặng 3 quyển sách hoặc 5 quyển sách. Kết quả cả lớp tặng được 146 quyển sách. Hỏi lớp 9B có bao nhiêu bạn tặng 3 quyển sách và bao nhiêu bạn tặng 5 quyển sách? Câu 4 (3,5 điểm): Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài đường tròn. Qua \(M\) kẻ tiếp tuyến \(MA\) với đường tròn \(\left( O \right)\)(\(A\) là tiếp điểm). Qua \(A\) kẻ đường thẳng song song với \(MO\) đường thẳng này cắt đường tròn \(\left( O \right)\) tại \(C\)(\(C\) khác \(A\)). Đường thẳng \(MC\) cắt đường tròn \(\left( O \right)\) tại điểm \(B\)(\(B\) khác \(C\)). Gọi \(H\) là hình chiếu của \(O\) lên \(BC\). a) Chứng minh tứ giác \(MAHO\) nội tiếp. b) Chứng minh \(\dfrac{{AB}}{{AC}} = \dfrac{{MA}}{{MC}}\). c) Chứng minh \(\angle BAH = {90^0}\). d) Vẽ đường kính \(AD\) của đường tròn \(\left( O \right)\). Chứng minh hai tam giác \(ACH\) và \(DMO\)đồng dạng. Câu 5 (0,5 điểm): Cho các số thực không âm \(a,\,\,b\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{\left( {{a^2} + 2b + 3} \right)\left( {{b^2} + 2a + 3} \right)}}{{\left( {2a + 1} \right)\left( {2b + 1} \right)}}\) Lời giải chi tiết Câu 1: Phương pháp: a) Khai phương biểu thức trong căn để tính giá trị của biểu thức b) Quy đồng các phân thức đại số, cộng các phân thức đại số để rút gọn biểu thức c) Sử dụng phương pháp cộng đại số để tìm nghiệm \(y\), sau đó thay vào phương trình (1) hoặc (2) để tìm nghiệm \(x\) và kết luận Cách giải: a) Ta có: \(2\sqrt {16} - \sqrt {25} = 2\sqrt {{4^2}} - \sqrt {{5^2}} \)\( = 2.4 - 5 = 3.\) b) Điều kiện: \(x > 0,\,\,x \ne 4.\) \(\begin{array}{l}A = \left( {\dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}} \right):\dfrac{{\sqrt x }}{{x - 4}}\\\,\,\,\, = \dfrac{{\sqrt x + 2 + \sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}.\dfrac{{x - 4}}{{\sqrt x }}\\\,\,\,\, = \dfrac{{2\sqrt x }}{{x - 4}}.\dfrac{{x - 4}}{{\sqrt x }} = 2.\end{array}\) Vậy \(A = 2.\) c) \(\left\{ \begin{array}{l}x + 4y = 9\\x + 3y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 7 - 3y\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 7 - 3.2\\y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right..\) Vậy hệ phương trình có nghiệm duy nhất: \(S = \left\{ {\left( {1;\,\,2} \right)} \right\}.\) Câu 2: Phương pháp: a) Thay \(m = - 2\) vào phương trình, sử dụng công thức nghiệm để giải phương trình bậc hai một ẩn hoặc đưa phương trình về phương trình tích để giải tìm nghiệm. b) Tính \(\Delta \) (hoặc \(\Delta '\)), phương trình có hai nghiệm phân biệt khi \(\Delta > 0\) (hoặc \(\Delta ' > 0\)), theo hệ thức vi – ét xác định tổng và tích của hai nghiệm của phương trình; biến đổi \({x_1}^2 + {x_2}^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\), khi tìm được \(m\) chú ý kiểm tra lại điều kiện. Cách giải: a) Với \(m = - 2\) phương trình trở thành: \({x^2} - 2x - 3 = 0\,\,\,\,\left( 1 \right)\) Ta có: \(\Delta ' = \dfrac{{{{\left( { - 1} \right)}^2} - \left( { - 3} \right)}}{1} = 4\), phương trình có hai nghiệm phân biệt \({x_1} = \dfrac{{1 + \sqrt 4 }}{1} = 3,\,\,\,{x_2} = \dfrac{{1 - \sqrt 4 }}{1} = - 1\) Vậy với \(m = - 2\), phương trình có tập nghiệm \(S = \left\{ { - 1;3} \right\}\). b) Xét phương trình: \({x^2} - 2x + m - 1 = 0\,\,\,\left( * \right)\) Phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) \( \Leftrightarrow \Delta ' > 0\)\( \Leftrightarrow 1 - \left( {m - 1} \right) > 0\) \( \Leftrightarrow 1 - m + 1 > 2 \Leftrightarrow m < 2.\) Với \(m < 2\) thì phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\) Áp dụng hệ thức Vi- ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m - 1\end{array} \right.\) Theo đề bài ta có: \({x_1}^2 + {x_2}^2 - 3{x_1}{x_2} = 2{m^2} + \left| {m - 3} \right|\) \(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 3{x_1}{x_2} = 2{m^2} + \left| {m - 3} \right|\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 5{x_1}{x_2} = 2{m^2} + \left| {m - 3} \right|\\ \Leftrightarrow {2^2} - 5\left( {m - 1} \right) = 2{m^2} + m - 3\,\,\,\,\left( {do\,\,m < 2 \Rightarrow \left| {m - 3} \right| = 3 - m} \right)\\ \Leftrightarrow 4 - 5m + 5 = 2{m^2} + 3 - m\\ \Leftrightarrow 2{m^2} + 4m - 6 = 0\\ \Leftrightarrow {m^2} + 2m - 3 = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\,\,\,\left( {tm} \right)\\m = - 3\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy với \(m \in \left\{ { - 3;1} \right\}\) thì thỏa mãn yêu cầu bài toán. Câu 3: Phương pháp: Gọi số học sinh tặng 3 quyển sách là \(x\) (học sinh), \(\left( {x \in {\mathbb{N}^*},\,\,x < 42} \right)\), số học sinh tặng 5 quyển sách là \(y\) (học sinh), \(\left( {y \in {\mathbb{N}^*},\,\,y < 42} \right)\), sau đó lập hệ phương trình để tìm ra \(x\) và \(y\) Cách giải: Gọi số học sinh tặng 3 quyển sách là \(x\) (học sinh), \(\left( {x \in {\mathbb{N}^*},\,\,x < 42} \right).\) số học sinh tặng 5 quyển sách là \(y\) (học sinh), \(\left( {y \in {\mathbb{N}^*},\,\,y < 42} \right).\) Tổng số bạn học sinh của lớp 9B là 42 bạn nên ta có: \(x + y = 42\,\,\,\,\left( 1 \right)\) Số sách mà \(x\) học sinh tặng được là: \(3x\) (quyển). Số sách mà \(y\) học sinh tặng được là: \(5y\) (quyển). Tổng số sách lớp 9B tặng được là 146 quyển nên ta có phương trình:\(3x + 5y = 146\,\,\,\,\left( 2 \right)\) Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 42\\3x + 5y = 146\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 3y = 126\\3x + 5y = 146\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2y = 20\\x = 42 - y\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}y = 10\,\,\,\left( {tm} \right)\\x = 42 - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 32\,\,\left( {tm} \right)\\y = 10\,\,\,\end{array} \right.\) Vậy lớp 9B có 32 học sinh tặng 3 quyển sách và 10 học sinh tặng 10 quyển sách. Câu 4: Phương pháp: a) Sử dụng dấu hiệu nhận biết của tứ giác nội tiếp: hai góc cùng nhìn một cạnh dưới các góc bằng nhau bằng nhau b) Chứng minh \(\Delta MAB \sim \Delta MCA\,\,\,\left( {g - g} \right)\) để suy ra hệ thức của đề bài c) Chứng minh \(\angle MAO = \angle MAB + \angle BAO = {90^0}\) để suy ra \(\angle BAH = {90^0}\) d) Chứng minh \(\angle AHC = \angle DOM\) và \(\dfrac{{AH}}{{OD}} = \dfrac{{HC}}{{OM}}\) Cách giải: a) Ta có: \(H\) là hình chiếu của \(O\) trên \(BC\) \( \Rightarrow OH \bot BC \Rightarrow \angle OHB = {90^0}\) hay \(\angle OHM = {90^0}\) Tứ giác \(MAHO\) có \(\angle MAO = \angle OHM = {90^0}\) Suy ra tứ giác \(MAHO\) nội tiếp (hai góc cùng nhìn một cạnh dưới các góc bằng nhau bằng nhau). b) Xét \(\Delta MAB\) và \(\Delta MCA\) ta có: \(\angle AMB\,\,\,chung\) \(\angle MAB = \angle MCA\) (góc tạo bởi tia tiếp tuyến và dây cùng, góc nội tiếp cùng chắn cung \(AB\)) \( \Rightarrow \Delta MAB \sim \Delta MCA\,\,\,\left( {g - g} \right)\) \( \Rightarrow \dfrac{{MA}}{{MC}} = \dfrac{{AB}}{{AC}}\) (đpcm). c) Ta có: \(\angle OAH = \angle CMO\) (do tứ giác \(MAHO\) nội tiếp) Lại có: \(\angle ACM = \angle CMO\) (hai góc so le trong) \( \Rightarrow \angle OAH = \angle ACM\,\,\,\left( { = \angle CMO} \right)\) Xét \(\left( O \right)\) ta có: \(\angle MAB = \angle ACM\) (cmt) \( \Rightarrow \angle OAH = \angle MAB\,\,\left( { = \angle ACM} \right).\) Lại có: \(\angle MAB + \angle BAO = \angle MAO = {90^0}\) \( \Rightarrow \angle BAO + \angle HAO = \angle BAH = {90^0}\) (đpcm). d) Ta có: tứ giác \(AMOH\) nội tiếp nên \(\angle AHM = \angle AOM\)( hai góc nội tiếp cùng chắn cung \(AM\)) Ta có: \(\left\{ \begin{array}{l}\angle AHM + \angle AHC = {180^0}\\\angle HOM + \angle DOM = {180^0}\end{array} \right.\)( hai góc kề bù) Từ đó suy ra: \(\angle AHC = \angle DOM\)\(\left( 1 \right)\) Xét \(\Delta AHB\)và \(\Delta AOM\) có: \(\left\{ \begin{array}{l}\angle BAH = \angle MAO = {90^0}\\\angle AHB = \angle AOM\end{array} \right.\) Suy ra \(\Delta AHB \sim \Delta AOM\)\(\left( {g.g} \right)\) \( \Rightarrow \dfrac{{AH}}{{OA}} = \dfrac{{HB}}{{OM}}\) (hai cạnh tương ứng) Tam giác \(OBC\) có \(OB = OC\) nên tam giác \(OBC\) cân tại \(O\), có \(OH \bot BC\) Nên \(OH\) đồng thời là đường trung tuyến \( \Rightarrow HB = HC\) Hay \(\dfrac{{AH}}{{OD}} = \dfrac{{HC}}{{OM}}\)\(\left( 2 \right)\) do \(\left( {OA = OD,\,\,HB = HC} \right)\) Từ \(\left( 1 \right),\left( 2 \right)\) suy ra: \(\Delta ACH \sim \Delta DMO\,\,\left( {c.g.c} \right)\,\,\,\left( {dpcm} \right)\). Câu 5: Phương pháp: Biến đổi tử số và mẫu số sao cho có nhân tử \({\left( {a + b + 1} \right)^2}\), sau đó rút gọn để tìm giá trị nhỏ nhất của của biểu thức \(P\) Cách giải: Ta có: \(\begin{array}{l}{a^2} + 2b + 3 = {a^2} + 1 + 2b + 2 \ge 2\left( {a + b + 1} \right)\\{b^2} + 2a + 3 = {b^2} + 1 + 2a + 2 \ge 2\left( {a + b + 1} \right)\end{array}\) \( \Rightarrow P \ge \dfrac{{4{{\left( {a + b + 1} \right)}^2}}}{{\left( {2a + 1} \right)\left( {2b + 1} \right)}} = \dfrac{{4{{\left( {a + b + 1} \right)}^2}}}{{4ab + 2\left( {a + b} \right) + 1}}\) Lại có: \(\begin{array}{l}ab \le {\left( {\dfrac{{a + b}}{2}} \right)^2} \Rightarrow 4ab \le {\left( {a + b} \right)^2}\\ \Rightarrow 4ab + 2\left( {a + b} \right) + 1 \le {\left( {a + b} \right)^2} + 2\left( {a + b} \right) + 1 = {\left( {a + b + 1} \right)^2}\\ \Rightarrow P \ge \dfrac{{4{{\left( {a + b + 1} \right)}^2}}}{{{{\left( {a + b + 1} \right)}^2}}} = 4\end{array}\) Dấu “=” xảy ra khi \(a = b = 1\). Vậy \({P_{\min }} = 4 \Leftrightarrow a = b = 1\).
|




















Danh sách bình luận