Đề thi vào 10 môn Toán Hà Tĩnh năm 2019Tải vềCâu 1 (2 điểm): Rút gọn các biểu thức sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
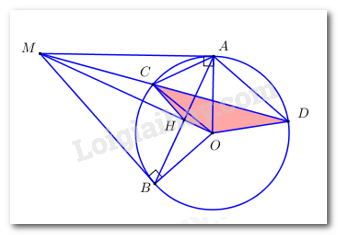
Đề bài Câu 1 (2 điểm): Rút gọn các biểu thức sau: \(a)\,A = \sqrt {50} - \sqrt {18} \,\) \(b)\,B = \left( {\dfrac{2}{{{a^2} + a}} - \dfrac{2}{{a + 1}}} \right):\dfrac{{1 - a}}{{{a^2} + 2a + 1}}\) với \(a \ne 0\) và \(a \ne \pm 1\) Câu 2 (2,5 điểm): a) Tìm các giá trị của \(a\) và \(b\) để đường thẳng \(\left( d \right):y = ax + b\) đi qua hai điểm \(M\left( {1;5} \right)\) và \(N\left( {2;8} \right)\) b) Cho phương trình \({x^2} - 6x + m - 3 = 0\) (\(m\) là tham số). Tìm giá trị của \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,{x_2}\) thỏa mãn \(\left( {{x_1} - 1} \right)\left( {x_2^2 - 5{x_2} + m - 4} \right) = 2\) Câu 3 (1,5 điểm): Một đội xe vận tải được phân công chở 112 tấn hàng. Trước giờ khởi hành có 2 xe phải đi làm nhiệm vụ khác nên mỗi xe còn lại phải chở thêm 1 tấn hàng so với dự tính. Tính số xe ban đầu của đội xe, biết rằng mỗi xe đều chở khối lượng hàng như nhau. Câu 4 (3 điểm): Cho đường tròn tâm O và điểm M nằm ngoài đường tròn đó. Qua M kẻ các tiếp tuyến \(MA;\,MB\) với đường tròn (\(A,\,B\) là tiếp điểm). Đường thẳng \(\left( d \right)\)thay đổi đi qua M, không đi qua O, và luôn cắt đường tròn tại hai điểm phân biệt \(C\) và \(D\) (C nằm giữa \(M\) và \(D\)) a) Chứng minh \(AMBO\) là tứ giác nội tiếp. b) Chứng minh \(MC.MD = M{A^2}.\) c) Chứng minh đường tròn ngoại tiếp \(\Delta OCD\) luôn đi qua điểm cố định khác \(O.\) Câu 5 (1 điểm): Cho hai số thực dương \(a,b\) thỏa mãn \(a + b + 3ab = 1.\) Tìm giá trị lớn nhất của biểu thức \(P = \dfrac{{6ab}}{{a + b}} - {a^2} - {b^2}.\) Lời giải Câu 1 Phương pháp: a) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,A < 0\end{array} \right..\) b) Quy đồng mẫu các phân thức, biến đổi rồi rút gọn biểu thức. Cách giải: Rút gọn các biểu thức: \(a)\,\,A = \sqrt {50} - \sqrt {18} = \sqrt {25.2} - \sqrt {9.2} = 5\sqrt 2 - 3\sqrt 2 = 2\sqrt 2 .\) Vậy \(A = 2\sqrt 2 .\) \(b)\,\,\,B = \left( {\dfrac{2}{{{a^2} + a}} - \dfrac{2}{{a + 1}}} \right):\dfrac{{1 - a}}{{{a^2} + 2a + 1}}\) với \(a \ne 0\) và \(a \ne \pm 1.\) Điều kiện: \(a \ne 0,\,\,a \ne \pm 1.\) \(\begin{array}{l}B = \left( {\dfrac{2}{{{a^2} + a}} - \dfrac{2}{{a + 1}}} \right):\dfrac{{1 - a}}{{{a^2} + 2a + 1}} = \left[ {\dfrac{2}{{a\left( {a + 1} \right)}} - \dfrac{2}{{a + 1}}} \right]:\dfrac{{1 - a}}{{{{\left( {a + 1} \right)}^2}}}\\ = \dfrac{{2 - 2a}}{{a\left( {a + 1} \right)}}.\dfrac{{{{\left( {a + 1} \right)}^2}}}{{1 - a}} = \dfrac{{2\left( {1 - a} \right)}}{a}.\dfrac{{a + 1}}{{1 - a}} = \dfrac{{2\left( {a + 1} \right)}}{a}.\end{array}\) Vậy với \(a \ne 0,\,\,a \ne \pm 1\) thì \(B = \dfrac{{2\left( {a + 1} \right)}}{a}.\) Câu 2: Phương pháp: a) Thay tọa độ điểm M và N vào phương trình đường thẳng, rút ra hệ phương trình hai ẩn a, b. Giải hệ phương trình tìm a, b. b) Tìm điều kiện để phương trình có 2 nghiệm phân biệt \(\left( {\Delta > 0} \right)\). Áp dụng định lí Vi-ét. Cách giải: a) \(M\left( {1;5} \right) \in d:\,\,\,y = ax + b \Rightarrow 5 = a + b\). \(N\left( {2;\,\,8} \right) \in d:\,\,y = ax + b \Rightarrow 8 = 2a + b\). Ta có hệ phương trình: \(\left\{ \begin{array}{l}a + b = 5\\2a + b = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = 5 - a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = 2\end{array} \right.\). Vậy \(a = 3,\,\,\,b = 2.\) b) \({x^2} - 6x + m - 3 = 0\,\,\,\,\left( 1 \right)\) Để phương tình có hai nghiệm phân biệt \({x_1},\,{x_2}\) thì \(\Delta ' > 0\). \( \Leftrightarrow 9 - m + 3 > 0 \Leftrightarrow 12 - m > 0 \Leftrightarrow m < 12.\) Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 6\\{x_1}{x_2} = m - 3\end{array} \right.\). Theo bài ra ta có: \(\left( {{x_1} - 1} \right)\left( {x_2^2 - 5{x_2} + m - 4} \right) = 2\,\,\left( * \right)\). Do \({x_2}\) là nghiệm của phương trình (1) nên \(\begin{array}{l}\,\,\,\,\,\,\,x_2^2 - 6{x_2} + m - 3 = 0\,\,\,\\ \Leftrightarrow x_2^2 - 5{x_2} + m - 4 - {x_2} + 1 = 0\\ \Leftrightarrow x_2^2 - 5{x_2} + m - 4 = {x_2} - 1\end{array}\) Khi đó \(\left( * \right) \Leftrightarrow \left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) = 2 \Leftrightarrow {x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 = 2\). \( \Leftrightarrow m - 3 - 6 + 1 = 2 \Leftrightarrow m = 10\,\,\left( {tm} \right)\). Vậy \(m = 10\). Câu 3 Phương pháp: Gọi số xe ban đầu của đội xe là \(x\) (xe) \(\left( {x > 2,\,\,x \in \mathbb{N}} \right).\) Dựa vào các giả thiết bài toán biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết rồi lập phương trình. Giải phương trình tìm ẩn \(x\) rồi đối chiếu với điều kiện sau đó kết luận. Cách giải: Gọi số xe ban đầu của đội xe là \(x\) (xe) \(\left( {x > 2,\,\,x \in \mathbb{N}} \right).\) Theo dự định, mỗi xe phải chở số tấn hàng là: \(\dfrac{{112}}{x}\) (tấn) Số xe thực tế làm nhiệm vụ là: \(x - 2\) (xe). \( \Rightarrow \) Thực tế, mỗi xe chở số tấn hàng là: \(\dfrac{{112}}{{x - 2}}\) (tấn). Thực tế, mỗi xe phải chở nhiều hơn theo dự định \(1\) tấn hàng nên ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\dfrac{{112}}{{x - 2}} - \,\dfrac{{112}}{x} = 1\\ \Leftrightarrow 112x - 112\left( {x - 2} \right) = x\left( {x - 2} \right)\\ \Leftrightarrow 112x - 112x + 224 = {x^2} - 2x\\ \Leftrightarrow {x^2} - 2x - 224 = 0\\ \Leftrightarrow {x^2} - 16x + 14x - 224 = 0\\ \Leftrightarrow x\left( {x - 16} \right) + 14\left( {x - 16} \right) = 0\\ \Leftrightarrow \left( {x - 16} \right)\left( {x + 14} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 16 = 0\\x + 14 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\,\,\left( {tm} \right)\\x = - 14\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy số xe ban đầu của đội xe là 16 xe. Câu 4: Phương pháp: a) Sử dụng định nghĩa tứ giác nội tiếp là tứ giác có tổng hai góc đối bằng 1800. b) Chứng minh tam giác \(MCA\) và tam giác \(MAD\) đồng dạng. c) Chứng minh tứ giác \(OHCD\) là tứ giác nội tiếp. Cách giải: a) Chứng minh \(AMBO\) là tứ giác nội tiếp Do \(MA,\,\,MB\) là các tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A,\,\,B\) nên \(\angle OAM = \angle OBM = {90^0}\). Xét tứ giác \(AMBO\) có: \(\angle OAM + \angle OBM = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(AMBO\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800). b) Chứng minh \(MC.MD = M{A^2}\). Xét tam giác \(MCA\) và tam giác \(MAD\) có: \(\angle AMD\) chung; \(\angle MAC = \angle MDA\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(AC\)); (1). c) Chứng minh đường tròn ngoại tiếp tam giác \(OCD\) luôn đi qua điểm cố định khác \(O\). Gọi \(H = OM \cap AB\,\,\left( {H \ne O} \right)\). Ta có \(OA = OB\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của \(AB\). \(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của \(AB\). \( \Rightarrow OM\) là trung trực của \(AB\) \( \Rightarrow OM \bot AB\) tại \(H\). Áp dụng hệ thức lượng trong tam giác vuông \(OAM\) ta có: \(M{A^2} = MH.MO\,\,\left( 2 \right)\). Từ (1) và (2) \( \Rightarrow MC.MD = MH.MO \Rightarrow \dfrac{{MC}}{{MH}} = \dfrac{{MO}}{{MD}}\). Xét tam giác \(MCH\) và tam giác \(MOD\) có : \(\angle OMD\) chung; \(\dfrac{{MC}}{{MH}} = \dfrac{{MO}}{{MD}}\,\,\left( {cmt} \right)\); (hai góc tương ứng). Mà \(\angle MHC + \angle OHC = {180^0}\) (kề bù) \( \Rightarrow \angle CDO + \angle & OHC = {180^0} \Rightarrow \) Tứ giác \(OHCD\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800). \( \Rightarrow H\) thuộc đường tròn ngoại tiếp tam giác \(OCD\). Mà \(O,\,\,M\) cố định \( \Rightarrow A,\,\,B\) cố định \( \Rightarrow H = OM \cap AB\) cố định. Vậy đường tròn ngoại tiếp tam giác \(OCD\) luôn đi qua điểm \(H = OM \cap AB\,\,\left( {H \ne O} \right)\) cố định (đpcm). Câu 5: Phương pháp: Sử dụng bất đẳng thức Cô-si. Cách giải: Theo đề bài ta có: \(a + b + 3ab = 1 \Leftrightarrow 3ab = 1 - \left( {a + b} \right) \Leftrightarrow ab = \dfrac{{1 - \left( {a + b} \right)}}{3}\) Áp dụng bất đẳng thức Cô-si ta có: \(ab \le \dfrac{{{{\left( {a + b} \right)}^2}}}{4}\) \(\begin{array}{l} \Rightarrow \dfrac{{1 - \left( {a + b} \right)}}{3} \le \dfrac{{{{\left( {a + b} \right)}^2}}}{4}\\ \Leftrightarrow 4 - 4\left( {a + b} \right) \le 3{\left( {a + b} \right)^2}\\ \Leftrightarrow 3{\left( {a + b} \right)^2} + 4\left( {a + b} \right) - 4 \ge 0\\ \Leftrightarrow 3{\left( {a + b} \right)^2} + 6\left( {a + b} \right) - 2\left( {a + b} \right) - 4 \ge 0\\ \Leftrightarrow 3\left( {a + b} \right)\left[ {\left( {a + b} \right) + 2} \right] - 2\left( {a + b + 2} \right) \ge 0\\ \Leftrightarrow \left( {a + b + 2} \right)\left[ {3\left( {a + b} \right) - 2} \right] \ge 0\\ \Leftrightarrow 3\left( {a + b} \right) - 2 \ge 0\,\,\,\,\left( {do\,\,\,a + b + 2 > 0\,\,\forall a,\,\,b > 0} \right)\\ \Leftrightarrow a + b \ge \dfrac{2}{3}.\\ \Rightarrow P = \dfrac{{6ab}}{{a + b}} - \left( {{a^2} + {b^2}} \right) = \dfrac{{2 - 2\left( {a + b} \right)}}{{a + b}} - \left( {{a^2} + {b^2}} \right)\\ \le \dfrac{2}{{a + b}} - 2 - \dfrac{{{{\left( {a + b} \right)}^2}}}{2} \le \dfrac{2}{{\dfrac{2}{3}}} - 2 - \dfrac{{{{\left( {\dfrac{2}{3}} \right)}^2}}}{2} = \dfrac{7}{9}.\end{array}\) Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b\\a + b = \dfrac{2}{3}\end{array} \right. \Leftrightarrow a = b = \dfrac{1}{3}.\) Vậy \(Max\,\,P = \dfrac{7}{9}\) khi \(a = b = \dfrac{1}{3}.\)
|




















Danh sách bình luận