Đề thi vào 10 môn Toán Hà Tĩnh năm 2021

Đề bài

Câu 1 (2,0 điểm):

Rút gọn các biểu thức sau:

a) $P = \sqrt {45}  + \sqrt {20}  - \sqrt 5$

b) $Q = \left( {\dfrac{1}{{2\sqrt x  + 1}} + \dfrac{1}{{2\sqrt x  - 1}}} \right):\dfrac{1}{{1 - 4x}}$ với $x \ge 0,x \ne \dfrac{1}{4}$

Câu 2 (1,0 điểm):

Trong mặt phẳng Oxy, cho hai đường thẳng $\left( d \right):\,\,y = mx + 3m + 2$ và $\left( {{d_1}} \right):\,\,y = x + 1$. Tìm giá trị của $m$ để hai đường thẳng $\left( d \right)$ và $\left( {{d_1}} \right)$ song song với nhau.

Câu 3 (2,0 điểm):

Cho phương trình ${x^2} - 2\left( {m + 1} \right)x + {m^2} = 0$ (m là tham số).

a) Giải phương trình với $m = 1$.

b) Tìm giá trị của $m$ để phương trình đã cho có hai nghiệm ${x_1},\,\,{x_2}$ thỏa mãn: $x_1^2 + x_2^2 + 6 = 4{x_1}{x_2}$

Câu 4 (1,0 điểm):

Giải sử giá tiền điện hàng tháng được tính theo bậc thang như sau:

Bậc 1: Từ 1 kWh đến $100$ kWh thì giá điện là: $1500$ đ/1kWh.

Bậc 2: Từ $101$ kWh đến $150$ kWh  thì giá điện là $2000$đ/1kWh.

Bậc 3: Từ $151$ kWh trở lên thì giá điện là $4000$ đ/1kWh.

(Ví dụ: Nếu dùng $170$ kWh thì có $100$ kWh tính theo giá bậc $1$, có $50$ kWh tính theo giá bậc $2$ và có $20$ kWh tính theo giá bậc 3).

Tháng 4 năm 2021 tổng số tiền điện của nhà bạn A và nhà bạn B là $560000$ đ. So với tháng 4 thì tháng 5 tiền điện nhà bạn A tăng $30\%$, nhà bạn B tăng $20\%$, do đó tổng số tiền điện của cả nhà hai bạn trong tháng 5 là $701000$đ. Hỏi tháng 4 nhà bạn A phải trả bao nhiêu tiền điện và dùng hết bao nhiêu kWh? ( biết rằng số tiền điện ở trên không tính thuế giá trị gia tăng).

Câu 5 (1,0 điểm):

Cho tam giác $ABC$ vuông tại $A$, có độ dài cạnh $AB = 3cm$, cạnh $AC = 4cm$. Gọi $AH$ là đường cao của tam giác, tính diện tích tam giác $AHC$.

Câu 6 (2,0 điểm):

Cho tam giác nhọn $ABC$ $\left( {AB < AC} \right)$ nội tiếp đường tròn tâm $O$, $E$ là điểm chính giữa cung nhỏ $BC$.

a) Chứng minh $\angle CAE = \angle BCE$ .

b) Gọi $M$ là điểm trên cạnh $AC$ sao cho $EM = EC$ ($M$ khác $C$); $N$ là giao điểm của $BM$ với đường tròn tâm $O$ ($N$ khác $B$). Gọi $I$ là giao điểm của $BM$ với $AE$; $K$ là giao điểm của $AC$ với $EN$. Chứng minh tứ giác $EKMI$ nội tiếp.

Câu 7 (1,0 điểm):

Cho các số thực không âm $a,\,\,b,\,\,c$ thỏa mãn $a + b + c = 2021$. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P = \sqrt {a + b}  + \sqrt {b + c}  + \sqrt {c + a}$. 

Lời giải

Câu 1:

Phương pháp:

a) Biến đổi biểu thức trong căn, khai phương rồi rút gọn biểu thức

b) Tìm mẫu thức chung, quy đồng các phân thức đại số, áp đụng quy tắc cộng, nhân, chia các phân thức đại số để rút gọn biểu thức

Cách giải:

a) Ta có:

$\begin{array}{l}P = \sqrt {45}  + \sqrt {20}  - \sqrt 5 \\\,\,\,\,\, = \sqrt {9.5}  + \sqrt {4.5}  - \sqrt 5 \\\,\,\,\, = 3\sqrt 5  + 2\sqrt 5  - \sqrt 5  = 4\sqrt 5 \end{array}$

Vậy $P = 4\sqrt 5$.

b) Với $x \ge 0,x \ne \dfrac{1}{4}$ ta có

$\begin{array}{l}Q = \left( {\dfrac{1}{{2\sqrt x  + 1}} + \dfrac{1}{{2\sqrt x  - 1}}} \right):\dfrac{1}{{1 - 4x}}\\\,\,\,\,\, = \dfrac{{2\sqrt x  - 1 + 2\sqrt x  + 1}}{{\left( {2\sqrt x  + 1} \right)\left( {2\sqrt x  - 1} \right)}}:\dfrac{1}{{1 - 4x}}\\\,\,\,\,\,\, = \dfrac{{4\sqrt x }}{{4x - 1}}:\dfrac{1}{{1 - 4x}}\\\,\,\,\,\, = \dfrac{{4\sqrt x }}{{4x - 1}}.\left( {1 - 4x} \right) = \dfrac{{4\sqrt x }}{{ - \left( {1 - 4x} \right)}}.\left( {1 - 4x} \right) =  - 4\sqrt x \end{array}$

Vậy $Q =  - 4\sqrt x$ với $x \ge 0,x \ne \dfrac{1}{4}$.

Câu 2:

Phương pháp:

Hai đường thẳng song song với nhau khi $a = a'$, $b \ne b'$

Cách giải:

Hai đường thẳng $\left( d \right)$ và $\left( {{d_1}} \right)$ song song với nhau khi và chỉ khi $\left\{ \begin{array}{l}m = 1\\3m + 2 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\m \ne  - \dfrac{1}{3}\end{array} \right. \Leftrightarrow m = 1$.

Vậy với $m = 1$ thì $\left( d \right)$ và $\left( {{d_1}} \right)$ song song với nhau.

Câu 3:

Phương pháp:

a) Thay $m = 1$ vào phương trình, áp dụng công thức nghiệm của phương trình bậc hai một ẩn để giải phương trình

b) Xác định điều kiện để phương trình có hai nghiệm phân biệt; biến đổi biểu thức để xuất hiện ${x_1} + {x_2};{x_1}{x_2}$; áp dụng hệ thức Vi – ét để tính ${x_1} + {x_2};{x_1}{x_2}$ sau đó thay vào biểu thức để tính $m$

Cách giải:

a) Với $m = 1$, phương trình đã cho trở thành ${x^2} - 4x + 1 = 0$.

Ta có $\Delta ' = {2^2} - 1 = 3 > 0$ nên phương trình có 2 nghiệm phân biệt $\left[ \begin{array}{l}{x_1} = \dfrac{{ - b' + \sqrt {\Delta '} }}{a} = 2 + \sqrt 3 \\{x_2} = \dfrac{{ - b' - \sqrt {\Delta '} }}{a} = 2 - \sqrt 3 \end{array} \right.$.

Vậy khi $m = 1$ tập nghiệm của phương trình là $S = \left\{ {2 \pm \sqrt 3 } \right\}$.

b) Ta có: $\Delta ' = {\left( {m + 1} \right)^2} - {m^2} = 2m + 1$.

Để phương trình đã cho có 2 nghiệm ${x_1},\,\,{x_2}$ thì $\Delta ' \ge 0 \Leftrightarrow 2m + 1 \ge 0 \Leftrightarrow m \ge  - \dfrac{1}{2}$.

Khi đó áp dụng định lí Vi-ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right)\\{x_1}{x_2} = {m^2}\end{array} \right.$.

Theo bài ra ta có:

$\begin{array}{l}\,\,\,\,\,\,\,x_1^2 + x_2^2 + 6 = 4{x_1}{x_2}\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + 6 = 4{x_1}{x_2}\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 6{x_1}{x_2} + 6 = 0\\ \Leftrightarrow 4{\left( {m + 1} \right)^2} - 6{m^2} + 6 = 0\\ \Leftrightarrow  - 2{m^2} + 8m + 10 = 0\,\,\left( 1 \right)\end{array}$

Ta có $a - b + c =  - 2 - 8 + 10 = 0$ nên phương trình có 2 nghiệm phân biệt $\left[ \begin{array}{l}{m_1} =  - 1\,\,\,\left( {ktm} \right)\\{m_2} =  - \dfrac{c}{a} =  - \dfrac{{10}}{{ - 2}} = 5\,\,\left( {tm} \right)\end{array} \right.$.

Vậy có 1 giá trị của $m$ thỏa mãn là $m = 5$.

Câu 4:

Phương pháp:

Gọi số tiền điện nhà bạn A phải trả trong tháng 4 là $x$, số tiền điện nhà bạn B phải trả trong tháng 4 là $y$ (chú ý điều kiện), dựa vào giả thiết tổng tiền điện tháng 4 của hai nhà A, B lập được một phương trình, dựa vào giả thiết tổng số tiền điện tháng 5 của hai nhà A, B, từ hai phương trình lậ được hệ phương trình, giải hệ tìm ra nghiệm và so sánh với điều kiện, kết luận.

Cách giải:

Gọi số tiền điện nhà bạn A phải trả trong tháng 4 là $x$ $\left( {x > 0} \right)$( đồng)

Số tiền điện nhà bạn B phải trả trong tháng 4 là $y\,\,\,\left( {y > 0} \right)$ ( đồng)

Theo bài ta cố tổng số tiền điện trong tháng 4 nhà bạn A và nhà bạn B phải trả là $560000$ nên ta có phương trình $x + y = 560000$$\left( 1 \right)$

Số tiền điện trong tháng 5 nhà bạn A phải trả là $x + 30\% x = 1,3x$ (đồng)

Số tiền điện trong tháng 5 nhà bạn B phải trả là: $y + 20\% y = 1,2y$ (đồng)

Theo bài ta có tổng số tiền điện trong tháng 5 nhà bạn A và nhà bạn B phải trả là $701000$ nên ta có phương trình: $1,3x + 1,2y = 701000$$\left( 2 \right)$

Từ $\left( 1 \right),\left( 2 \right)$ ta có hệ phương trình: $\left\{ \begin{array}{l}x + y = 560000\\1,3x + 1,2y = 701000\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 560000 - y\\1,3\left( {560000 - y} \right) + 1,2y = 701000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 560000 - y\\728000 - 0,1y = 701000\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 560000 - y\\0,1y = 27000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 290000\\y = 270000\end{array} \right.\,\,\,\,\left( {tm} \right)$

Vậy số tiền điện nhà bạn A phải trả trong tháng 4 là $290000$đồng.

Nhận thấy: $290000 = 100.1500 + 50.2000 + 10.4000$

Vậy số điện nhà bạn A dùng trong tháng 4 là $100 + 50 + 10 = 160$ (kWh).

Câu 5:

Phương pháp:

+ Áp dụng hệ thức lượng trong tam giác vuông $ABC$: $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$ để tính độ dài đoạn $AH$

+ Áp dụng định lí Pytago trong tam giác vuông $AHC$: $A{C^2} = A{H^2} + H{C^2}$ để tính độ dài đoạn $HC$

Từ đó tính được diện tích $\Delta AHC$: ${S_{\Delta AHC}} = \dfrac{1}{2}AH.HC$

Cách giải:

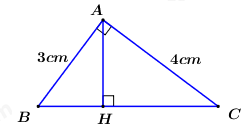
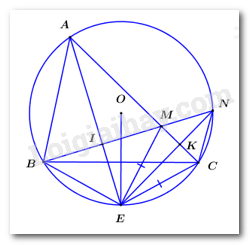
Áp dụng hệ thức lượng trong tam giác vuông $ABC$ ta có:

$\begin{array}{l}\,\,\,\,\,\,\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\\ \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}}\\ \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{9} + \dfrac{1}{{16}}\\ \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{{25}}{{144}}\\ \Rightarrow AH = \dfrac{{144}}{{25}}\\ \Rightarrow AH = \dfrac{{12}}{5}\,\,\left( {cm} \right)\end{array}$

Áp dụng định lí Pytago trong tam giác vuông $AHC$ ta có:

$\begin{array}{l}\,\,\,\,\,A{C^2} = A{H^2} + H{C^2}\\ \Rightarrow {4^2} = {\left( {\dfrac{{12}}{5}} \right)^2} = H{C^2}\\ \Rightarrow H{C^2} = 16 - \dfrac{{144}}{{25}}\\ \Rightarrow H{C^2} = \dfrac{{256}}{{25}}\\ \Rightarrow HC = \dfrac{{16}}{5}\,\,\left( {cm} \right)\end{array}$

Vì tam giác $AHC$ vuông tại $H$ nên ${S_{\Delta AHC}} = \dfrac{1}{2}AH.HC = \dfrac{1}{2}.\dfrac{{12}}{5}.\dfrac{{16}}{5} = \dfrac{{96}}{{25}}\,\,\left( {c{m^2}} \right)$.

Câu 6:

Phương pháp:

a) Vận dụng mối quan hệ góc nội tiếp trong đường tròn

b) Sử dụng dấu hiệu nhận biết của tứ giác nội tiếp: tứ giác có tổng hai góc bằng ${180^0}$ là tứ giác nội tiếp, từ đó chứng minh $\angle EKM + \angle EIM = {180^0}$

Cách giải:

a) Vì $E$ là điểm chính giữa của cung nhỏ $BC$ nên $sdcBE = sdcCE$.

$\Rightarrow \angle CAE = \angle BCE$ (trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).

b) Vì $EM = EC\,\,\left( {gt} \right)$, mà $EB = EC\,\,\left( {do\,\,sdcEB = sdcEC} \right)$ $\Rightarrow EB = EM$.

$\Rightarrow \Delta EBM$ cân tại $M$ $\Rightarrow \angle EBM = \angle EMB$ (2 góc ở đáy).

Ta có: $\angle EBM + \angle ECN = {180^0}$ (2 góc đối diện của tứ giác nội tiếp $BECN$)

            $\angle EMB + \angle EMN = {180^0}$ (kề bù)

$\Rightarrow \angle ECN = \angle EMN$.

Lại có $\angle ENC = \angle ENM$ (2 góc nội tiếp chắn hai cung bằng nhau)

$\begin{array}{l} \Rightarrow \angle ECN + \angle ENC = \angle EMN + \angle ENM\\ \Rightarrow {180^0} - \angle CEN = {180^0} - \angle MEN\\ \Rightarrow \angle CEN = \angle MEN\end{array}$

$\Rightarrow EK$ là phân giác của $\angle MEC$.

Mà tam giác $EMC$ cân tại $E\,\,\left( {EM = EC} \right)$ nên $EK$ đồng thời là đường cao $\Rightarrow EK \bot MC$.

$\Rightarrow \angle EKM = {90^0}$.

$\Rightarrow \angle EAK + \angle AEK = {90^0}$.

Mà $\angle EAK = \angle EAC = \angle BNE$ (2 góc nội tiếp chắn hai cung bằng nhau)

$\Rightarrow \angle BNE + \angle AEK = {90^0} \Rightarrow \angle BNI + \angle IEN = {90^0}$ $\Rightarrow \angle EIN$ vuông tại $I$.

$\Rightarrow \angle EIN = {90^0} \Rightarrow \angle EIM = {90^0}$.

Xét tứ giác $EKMI$ có: $\angle EKM + \angle EIM = {90^0} + {90^0} = {180^0}$.

Vậy $EKMI$ là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng ${180^0}$).

Câu 7:

Phương pháp:

+ Tìm giá trị lớn nhất: Áp dụng BĐT Buniacopxki cho ba số $\sqrt {a + b}$, $\sqrt {b + c}$, $\sqrt {c + a}$

+ Tìm giá trị nhỏ nhất: lập luận từ giả thiết để chứng minh $\sqrt {a + b}  \ge \dfrac{{a + b}}{{\sqrt {2021} }}$, $\sqrt {b + c}  \ge \dfrac{{b + c}}{{\sqrt {2021} }},$$\sqrt {c + a}  \ge \dfrac{{c + a}}{{\sqrt {2021} }}$ sau đó cộng vế với vế, nhóm các hạng tử chung lại với nhau để có điều phải chứng minh

Cách giải:

* Tìm giá trị lớn nhất

Ta có: $P = \sqrt {a + b}  + \sqrt {b + c}  + \sqrt {c + a}$

$\Rightarrow {P^2} = {\left( {\sqrt {a + b}  + \sqrt {b + c}  + \sqrt {c + a} } \right)^2} \le 3\left( {a + b + b + c + c + a} \right) = 6.2021 = 12126$ (BĐT Buniacopxki)

$\Rightarrow {P^2} \le 12126 \Leftrightarrow P \le \sqrt {12126}$.

Dấu “=” xảy ra $\Leftrightarrow 2021 - c = 2021 - a = a + c \Leftrightarrow \left\{ \begin{array}{l}a = c\\2021 - a = 2a\end{array} \right. \Leftrightarrow a = c = \dfrac{{2021}}{3} = b$.

Vậy ${P_{\max }} = \sqrt {12126}  \Leftrightarrow a = b = c = \dfrac{{2021}}{3}$.

* Tìm giá trị nhỏ nhất

Ta có: $a,\,\,b,\,\,c$ là các số thực không âm và $a + b + c = 2021$ nên $a + b \le 2021$.

$\Leftrightarrow \dfrac{1}{{a + b}} \ge \dfrac{1}{{2021}} \Leftrightarrow \dfrac{{{{\left( {a + b} \right)}^2}}}{{a + b}} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{2021}} \Leftrightarrow a + b \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{2021}} \Leftrightarrow \sqrt {a + b}  \ge \dfrac{{a + b}}{{\sqrt {2021} }}$.

Chứng minh hoàn toàn tương tự ta có: $\sqrt {b + c}  \ge \dfrac{{b + c}}{{\sqrt {2021} }},\,\,\sqrt {c + a}  \ge \dfrac{{c + a}}{{\sqrt {2021} }}$.

Khi đó ta có

$\begin{array}{l}P = \sqrt {a + b}  + \sqrt {b + c}  + \sqrt {c + a}  \ge \dfrac{1}{{\sqrt {2021} }}\left( {a + b + b + c + c + a} \right)\\ \Rightarrow P \ge \dfrac{2}{{\sqrt {2021} }}\left( {a + b + c} \right) = \dfrac{2}{{\sqrt {2021} }}.2021 = 2\sqrt {2021} \end{array}$

Dấu “=” xảy ra khi và chỉ khi $\left[ \begin{array}{l}a = b = 0,\,\,c = 2021\\a = c = 0,\,\,b = 2021\\b = c = 0,\,\,a = 2021\end{array} \right.$.

Vậy ${P_{\min }} = 2\sqrt {2021}$ khi $\left[ \begin{array}{l}a = b = 0,\,\,c = 2021\\a = c = 0,\,\,b = 2021\\b = c = 0,\,\,a = 2021\end{array} \right.$.