Đề thi vào 10 môn toán có đáp án - 9 năm gần nhất

Đề thi vào 10 môn Toán Hà Tĩnh năm 2023

Tải về

Câu 1: Rút gọn các biểu thức sau: a) $A = \sqrt {48} - 3\sqrt 3 $. b) $B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}$ (với $\left. {x > 0;x \ne 4} \right)$.

Quảng cáo

Lựa chọn câu để xem lời giải nhanh hơn

Tải về

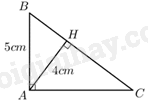
Đề bài

Câu 1: Rút gọn các biểu thức sau:

a) $A = \sqrt {48} - 3\sqrt 3 $.

b) $B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}$ (với $\left. {x > 0;x \ne 4} \right)$.

Câu 2:

a) Cho hai đường thẳng $\left( {{d_1}} \right):y = (m - 3)x + 4\left( m \right.$ là tham số) và $\left( {{d_2}} \right):y = 2x - 1$. Tìm giá trị của $m$ để hai đường thẳng $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$ song song với nhau.

b) Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 8}\end{array}} \right.$.

Câu 3: Cho phương trình ${x^2} - 2mx + {m^2} - m - 2 = 0$ (m là tham số). Tìm giá trị của m để phương trình đã cho có 2 nghiệm phân biệt ${x_1},{x_2}$ thỏa mãn $\frac{{{x_1}{x_2} + 1}}{{x_1^2 + x_2^2 + 2\left( {1 + {x_1}{x_2}} \right)}} = \frac{1}{6}.$

Câu 4: Một phòng họp ban đầu có 96 ghế được xếp thành các dãy và số ghế trong mỗi dãy đều bằng nhau. Có một lần phòng họp phải cất bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1 ghế (số ghế trong các dãy vẫn bằng nhau) để vừa đủ chỗ ngồi cho 110 đại biểu. Hỏi ban đầu trong phòng họp có bao nhiêu dãy ghế?

Câu 5: Cho tam giác ABC vuông tại A, đường cao AH ($H \in BC$). Biết độ dài đoạn $AB = 5cm$ và $AH = 4cm.$ Tính độ dài đoạn BH và diện tích tam giác ABC.

Câu 6: Cho tam giác ABC nhọn. Đường tròn (O) đường kính BC cắt các cạnh AB, AC lần lượt tại D và E (D khác B và E khác C). Gọi H là giao điểm của hai đường thẳng BE và CD.

a) Chứng minh ADHE là tứ giác nội tiếp.

b) Đường thẳng AH cắt BC tại F và cắt đường tròn (O) tại điểm P (P nằm giữa A và H). Đường thẳng DF cắt đường tròn (O) tại điểm K (K khác D). Gọi M là giao điểm của EK và BC, I là tâm đường tròn ngoại tiếp tam giác HDP. Chứng minh $C{E^2} = BC.MC$ và ba điểm B, I, P thẳng hàng.

Câu 7: Cho a, b, c là các số thực khác không. Tim giá trị nhỏ nhất của biểu thức:

$P = \frac{{{a^2}}}{{{a^2} + 2{{(b + c)}^2}}} + \frac{{{b^2}}}{{{b^2} + 2{{(c + a)}^2}}} + \frac{{{c^2}}}{{{c^2} + 2{{(a + b)}^2}}}.$

----- HẾT -----

Lời giải chi tiết

Câu 1 (VD):

Phương pháp:

a) Căn bậc hai của một số $a$ là một số $x$ sao cho ${x^2} = a$

b) Quy đồng và rút gọn sử dụng hằng đẳng thức.

Cách giải:

a) $A = \sqrt {48} - 3\sqrt 3 $.

Ta có: $A = \sqrt {48} - 3\sqrt 3 = \sqrt {{{3.4}^2}} - 3\sqrt 3 = 4\sqrt 3 - 3\sqrt 3 = \sqrt 3 $

Vậy $A = \sqrt 3 .$

b) $B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}$ (với $\left. {x > 0;x \ne 4} \right)$.

Với $x > 0;x \ne 4$ ta có:

$\begin{array}{l}B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}\\\,\,\, = \left( {\frac{{\sqrt x - 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} + \frac{{\sqrt x + 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}} \right).\frac{{x - 4}}{{\sqrt x }}\\\,\,\, = \frac{{2\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}.\frac{{x - 4}}{{\sqrt x }}\\\,\,\, = \frac{{2\sqrt x }}{{x - 4}}.\frac{{x - 4}}{{\sqrt x }}\\\,\,\, = 2\end{array}$

Vậy $B = 2.$

Câu 2 (VD):

Phương pháp:

a) Để hai đường thẳng song song thì hệ số góc bằng nhau.

b) Sử dụng phương pháp thế hoặc phương pháp trừ vế.

Cách giải:

a) Cho hai dường thẳng $\left( {{d_1}} \right):y = (m - 3)x + 4\left( m \right.$ là tham số) và $\left( {{d_2}} \right):y = 2x - 1$. Tìm giá trị của $m$ để hai đường thẳng $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$ song song với nhau.

Để $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$ song song với nhau thì $\left\{ \begin{array}{l}m - 3 = 2\\4 \ne - 1\end{array} \right. \Leftrightarrow m = 5$.

Vậy với $m = 5$ thì hai đường thẳng $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$ song song với nhau.

b) Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 8}\end{array}} \right.$.

$\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 8}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 2x - 3\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)}\\{3x + 2y = 8\,\,\,\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.$

Thay (1) vào (2) ta có

$\begin{array}{l}\left( 2 \right) \Leftrightarrow 3x + 2\left( {2x - 3} \right) = 8\\ \Leftrightarrow 3x + 4x - 6 = 8\\ \Leftrightarrow 7x = 14\\ \Leftrightarrow x = 2.\end{array}$

Thay $x = 2$ vào (1) ta được $y = 2.2 - 3 = 1$.

Vậy hệ phương trình có nghiệm $\left( {x;y} \right) = \left( {2;1} \right)$.

Câu 3 (VD):

Phương pháp:

Sử dụng định lí Vi – ét.

Nếu phương trình $a{x^2} + bx + c = 0(a \ne 0)$ có 2 nghiệm ${x_1},{x_2}$ thì

$\left\{ {\begin{array}{*{20}{l}}{S = {X_1} + {X_2} = \frac{{ - b}}{a}}\\{P = {x_1} \cdot {X_2} = \frac{c}{a}}\end{array}} \right.$

Cách giải:

Ta có $\Delta ' = {m^2} - \left( {{m^2} - m - 2} \right) = {m^2} - {m^2} + m + 2 = m + 2$

Để phương trình có 2 nghiệm phân biệt thì $\Delta ' > 0 \Leftrightarrow m + 2 > 0 \Leftrightarrow m > - 2$

Vậy $m > - 2$ thì phương trình có 2 nghiệm phân biệt ${x_1},{x_2}$

Áp dụng hệ thức Viet có $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = {m^2} - m - 2\end{array} \right.$

Để $\frac{{{x_1}{x_2} + 1}}{{x_1^2 + x_2^2 + 2\left( {1 + {x_1}{x_2}} \right)}} = \frac{1}{6}.$

$ \Leftrightarrow \frac{{{x_1}{x_2} + 1}}{{x_1^2 + x_2^2 + 2{x_1}{x_1} + 2}} = \frac{1}{6}$

$ \Leftrightarrow \frac{{{x_1}{x_2} + 1}}{{{{\left( {{x_1} + {x_2}} \right)}^2} + 2}} = \frac{1}{6}$

$ \Leftrightarrow \frac{{{m^2} - m - 2 + 1}}{{{{\left( {2m} \right)}^2} + 2}} = \frac{1}{6}$

$ \Leftrightarrow \frac{{{m^2} - m - 1}}{{4{m^2} + 2}} = \frac{1}{6}$

$ \Leftrightarrow 6{m^2} - 6m - 6 = 4{m^2} + 2$

$ \Leftrightarrow 2{m^2} - 6m - 8 = 0$

$ \Leftrightarrow 2\left( {m + 1} \right)\left( {m - 4} \right) = 0$

$ \Leftrightarrow \left[ \begin{array}{l}m = - 1\left( {TM} \right)\\m = 4\left( {TM} \right)\end{array} \right.$

Vậy m = -1 hoặc m = 4 thỏa mãn bài toán.

Câu 4 (VD):

Phương pháp:

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.

Cách giải:

Gọi x là số dãy ghế ban đầu. $\left( {x > 2,x \in {N^*}} \right)$.

Sau khi cất đi 2 dãy ghế, số dãy ghế còn lại là: $x - 2$ (dãy).

Số ghế ở mỗi hàng lúc ban đầu là $\frac{{96}}{x}$ (ghế).

Số ghế ở mỗi hàng sau khi bỏ bớt hai hàng là $\frac{{110}}{{x - 2}}$ (ghế).

Vì khi cất bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1 ghế nên ta có phương trình:

$\frac{{110}}{{x - 2}} - \frac{{96}}{x} = 1$

$ \Leftrightarrow \frac{{110x}}{{\left( {x - 2} \right)x}} - \frac{{96\left( {x - 2} \right)}}{{\left( {x - 2} \right)x}} = 1$

$ \Leftrightarrow \frac{{110x - 96\left( {x - 2} \right)}}{{\left( {x - 2} \right)x}} = 1$

$ \Leftrightarrow \frac{{110x - 96x + 192}}{{\left( {x - 2} \right)x}} = 1$

$ \Leftrightarrow \frac{{14x + 192}}{{\left( {x - 2} \right)x}} = 1$

$ \Leftrightarrow 14x + 192 = {x^2} - 2x$

$ \Leftrightarrow {x^2} - 16x - 192 = 0$

$ \Leftrightarrow \left( {x - 24} \right)\left( {x + 8} \right) = 0$

$ \Leftrightarrow \left[ \begin{array}{l}x = 24\left( {tm} \right)\\x = - 8\left( {ktm} \right)\end{array} \right.$

Vậy số dãy ghế lúc đầu là 24 dãy ghế.

Câu 5 (VD):

Phương pháp:

Áp dụng định lí Pytago và hệ thức lượng trong tam giác cho tam giác ABC vuông tại A đường cao AH ta được: $A{B^2} = BH.BC$.

Cách giải:

Áp dụng định lý Pytago cho tam giác ABH vuông tại H ta được: $A{H^2} + B{H^2} = A{B^2}$

$ \Rightarrow {4^2} + B{H^2} = {5^2}$

$\begin{array}{l} \Leftrightarrow 16 + B{H^2} = 25\\ \Leftrightarrow B{H^2} = 9\\ \Leftrightarrow BH = 3\end{array}$

Áp dụng hệ thức lượng cho tam giác ABC vuông tại A đường cao AH ta được: $A{B^2} = BH.BC$

$ \Rightarrow BC = \frac{{A{B^2}}}{{BH}} = \frac{{{5^2}}}{3} = \frac{{25}}{3}$

Diện tích tam giác ABC là: ${S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.4.\frac{{25}}{3} = \frac{{50}}{3}\left( {c{m^2}} \right)$

Câu 6 (VD):

Cách giải:

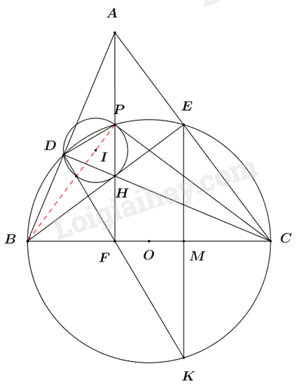
a) Chứng minh ADHE là tứ giác nội tiếp.

Ta có $\angle BEC = \angle BDC = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

$ \Rightarrow \angle ADH = \angle AEH = {90^0}$.

$ \Rightarrow \angle ADH + \angle AEH = {90^0} + {90^0} = {180^0}$

$ \Rightarrow ADHE$ là tứ giác nội tiếp

(Tứ giác có tổng hai góc đối bằng ${180^0}$).

+) Chứng minh CE²= BC.MC.

Xét tam giác ABC có: $\angle BEC = \angle BDC = {90^0}\,\,\left( {cmt} \right) \Rightarrow BE \bot AC,\,\,CD \bot AB$.

Mà $BE \cap CD = \left\{ H \right\} \Rightarrow H$ là trực tâm của tam giác ABC.

$ \Rightarrow AH \bot BC$ tại F $ \Rightarrow AF \bot BC \Rightarrow \angle BFH = {90^0}$.

Xét tứ giác BFHD có: $\angle BFH + \angle BDH = {90^0} + {90^0} = {180^0}$

$ \Rightarrow BFHD$ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng ${180^0}$).

$ \Rightarrow \angle DFH = \angle DBH = \angle DBE$ (hai góc nội tiếp cùng chắn cung DH)

Mà $\angle DBE = \angle DKE$ (hai góc nội tiếp cùng chắn cung DE)

$ \Rightarrow \angle DFH = \angle DKE$. Mà 2 góc này ở vị trí hai góc đồng vị bằng nhau.

$ \Rightarrow FP//KE \Rightarrow AF//KE$ (dhnb).

Mà $AF \bot BC\,\,\left( {cmt} \right) \Rightarrow KE \bot BC$ tại M $ \Rightarrow EM \bot BC$.

Xét tam giác BCE vuông tại E, đường cao EM có: $C{E^2} = BC.MC$ (hệ thức lượng trong tam giác vuông) (đpcm).

+) Chứng minh ba điểm B, I, P thẳng hàng.

Xét $\Delta CHF$ và $\Delta CBD$ có:

$\begin{align} \angle CFH=\angle CDB={{90}^{0}} \\ \angle BCD\,\,chung \\ \Rightarrow \Delta CHF\backsim \Delta CBD\,\,\left( g.g \right) \\ \end{align}$

$ \Rightarrow \frac{{CH}}{{CB}} = \frac{{CF}}{{CD}}$ (cặp cạnh tương ứng tỉ lệ)

$ \Rightarrow CH.CD = CB.CF$ (1)

Ta có: $\angle CPB = {90^0}$ (góc nội tiếp chắn nửa đường tròn) $ \Rightarrow \Delta CBP$ vuông tại P.

Xét tam giác CBP vuông tại P, đường cao PF có:

$C{P^2} = CB.CF$ (hệ thức lượng trong tam giác vuông) (2)

Từ (1) và (2) $ \Rightarrow CH.CD = C{P^2} \Rightarrow \frac{{CH}}{{CP}} = \frac{{CP}}{{CD}}$.

Xét $\Delta CHP$ và $\Delta CPD$ có:

$\begin{align}\angle PCD\,\,chung \\ \frac{CH}{CP}=\frac{CP}{CD}\,\,\left( cmt \right) \\ \Rightarrow \Delta CHP\backsim \Delta CPD\,\,\left( c.g.c \right) \\ \end{align}$

$ \Rightarrow \angle HPC = \angle PDC = \angle PDH$ (2 góc tương ứng).

Ta có $\angle HPI = \frac{{{{180}^0} - \angle HIP}}{2} = {90^0} - \frac{{\angle HIP}}{2} = {90^0} - \angle PDH$ (góc ở tâm và góc nội tiếp cùng chắn cung HP)

$ \Rightarrow \angle HIP = {90^0} - \angle HPC \Leftrightarrow \angle HIP + \angle HPC = {90^0} \Leftrightarrow \angle CPI = {90^0}$

$ \Rightarrow IP \bot PC$ (3)

Mà $\angle CPB = {90^0}$ (cmt) $ \Rightarrow BP \bot PC$ (4)

Từ (3) và (4) $ \Rightarrow B,\,\,I,\,\,P$ thẳng hàng (đpcm).

Câu 7 (VDC):

Phương pháp:

Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki.

Cách giải:

Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki ta có:

${\left( {a + b} \right)^2} \le \left( {1 + 1} \right)\left( {{a^2} + {b^2}} \right) = 2\left( {{a^2} + {b^2}} \right)$

${\left( {b + c} \right)^2} \le 2\left( {{b^2} + {c^2}} \right)$

${\left( {c + a} \right)^2} \le 2\left( {{c^2} + {a^2}} \right)$

Suy ra: $P\, \ge \frac{{{a^2}}}{{{a^2} + 4({b^2} + {c^2})}} + \frac{{{b^2}}}{{{b^2} + 4({c^2} + {a^2})}} + \frac{{{c^2}}}{{{c^2} + 4({a^2} + {b^2})}}$

$\,\,\, = \frac{{{a^2}}}{{{a^2} + 4({b^2} + {c^2})}} + \frac{1}{3} + \frac{{{b^2}}}{{{b^2} + 4({c^2} + {a^2})}} + \frac{1}{3} + \frac{{{c^2}}}{{{c^2} + 4({a^2} + {b^2})}} + \frac{1}{3} - 1$

$\,\,\, = \frac{{4({a^2} + {b^2} + {c^2})}}{{3\left( {{a^2} + 4({b^2} + {c^2})} \right)}} + \frac{{4({a^2} + {b^2} + {c^2})}}{{3\left( {{b^2} + 4({c^2} + {a^2})} \right)}} + \frac{{4({a^2} + {b^2} + {c^2})}}{{3\left( {{c^2} + 4({a^2} + {b^2})} \right)}} - 1$

$\,\,\, = \frac{4}{3}({a^2} + {b^2} + {c^2})\left( {\frac{1}{{{a^2} + 4({b^2} + {c^2})}} + \frac{1}{{{b^2} + 4({c^2} + {a^2})}} + \frac{1}{{{c^2} + 4({a^2} + {b^2})}}} \right) - 1$

Áp dụng bất đẳng thức cộng mẫu số ta được:

$\frac{1}{{{a^2} + 4({b^2} + {c^2})}} + \frac{1}{{{b^2} + 4({c^2} + {a^2})}} + \frac{1}{{{c^2} + 4({a^2} + {b^2})}} \ge \frac{{{{\left( {1 + 1 + 1} \right)}^2}}}{{9\left( {{a^2} + {b^2} + {c^2}} \right)}} = \frac{1}{{{a^2} + {b^2} + {c^2}}}$

Do đó: $P \ge \frac{4}{3}.\left( {{a^2} + {b^2} + {c^2}} \right).\frac{1}{{{a^2} + {b^2} + {c^2}}} - 1 = \frac{4}{3} - 1 = \frac{1}{3}$

Dấu “=” xảy ra khi và chỉ khi $a = b = c$

Vậy giá trị nhỏ nhất của $P$ là $\frac{1}{3}$ khi $a = b = c$.