Đề thi vào 10 môn Toán Sơn La năm 2022Tải vềI. TRẮC NGHIỆM (2,0 điểm) (Chọn phương án trả lời đúng và viết vào phần giấy kiểm tra) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài I. TRẮC NGHIỆM (2,0 điểm) (Chọn phương án trả lời đúng và viết vào phần giấy kiểm tra) Câu 1: Rút gọn biểu thức \(P = \sqrt {16{a^2}b} \) với \(a \ge 0,b \ge 0\). A. \(P = 4a\sqrt b \) B. \(16a\sqrt b \) C. \(P = 4{a^2}\sqrt b \) D. \(P = 4{a^2}b\) Câu 2: Đồ thị hàm số \(y = - 2x + 1\) đi qua điểm nào dưới đây? A. \(M\left( {0; - 1} \right)\) B. \(N\left( {0;1} \right)\) C. \(Q\left( {1;0} \right)\) D. \(P\left( {1; - 2} \right)\) Câu 3: Cho tam giác \(ABC\) vuông tại \(A\).
Khẳng định nào sau đây đúng? A. \(\tan C = \dfrac{{AB}}{{BC}}\) B. \(\tan C = \dfrac{{AC}}{{AB}}\) C. \(\tan C = \dfrac{{AC}}{{BC}}\) D. \(\tan C = \dfrac{{AB}}{{AC}}\) Câu 4: Phương trình \(x + 2y - 1 = 0\) có một nghiệm \(\left( {x;y} \right)\) là: A. \(\left( {0;0} \right)\) B. \(\left( {1;2} \right)\) C. \(\left( {1;0} \right)\) D. \(\left( {1; - 1} \right)\) Câu 5: Phương trình nào dưới đây là phương trình bậc hai một ẩn? A. \(2x + y - 1 = 0\) B. \({x^2} - 2x + 3 = 0\) C. \(3x - 5 = 0\) D. \({x^4} - 2{x^2} - 4 = 0\) Câu 6: Tìm \(a\) để đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(M\left( {1;2} \right)\) A. \(a = 2\) B. \(a = 1\) C. \(a = 4\) D. \(a = \sqrt 2 \) Câu 7: Trong một đường tròn, nếu góc nội tiếp chắn cung có số đo \({80^0}\) thì số đo góc nội tiếp đó bằng: A. \({20^0}\) B. \({80^0}\) C. \({40^0}\) D. \({60^0}\) Câu 8: Nếu phương trình \(a{x^2} + bx + c = 0\) với \(a \ne 0\) có hai nghiệm \({x_1}\) và \({x_2}\), thì \({x_1} + {x_2}\) bằng: A. \(\dfrac{b}{a}\) B. \(\dfrac{c}{a}\) C. \( - \dfrac{c}{a}\) D. \( - \dfrac{b}{a}\) Câu 9: Công thức tính diện tích mặt cầu bán kính R là: A. \(S = 4\pi {R^2}\) B. \(S = 4\pi R\) C. \(S = \dfrac{4}{3}\pi {R^2}\) D. \(S = 2\pi {R^2}\) Câu 10: Cho tứ giác ABCD nội tiếp đường tròn (O), khi đó số đo góc \(\angle B + \angle D\) bằng: A. \({360^0}\) B. \({120^0}\) C. \({90^0}\) D. \({180^0}\)
II. TỰ LUẬN (8,0 điểm) Câu 1 (2,0 điểm): a) Tìm điều kiện xác định của biểu thức: \(A = \sqrt {x + 1} + \sqrt {x - 2} \) b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 3\\2x + y = 6\end{array} \right.\) c) Giải phương trình: \({x^2} - 3x - 4 = 0\) Câu 2 (1,0 điểm): Một người đi xe máy từ A đến B với vận tốc 30km/h; lúc trở về người đó đi với vận tốc 40km/h nên thời gian về ít hơn thời gian lúc đi là 30 phút. Tính quãng đường AB. Câu 3 (1,0 điểm): Cho phương trình \(2{x^2} + \left( {2m - 1} \right)x - m - 1 = 0\) với \(m\) là tham số, biết phương trình có hai nghiệm \({x_1},{x_2}\). Tìm \(m\) để biểu thức \(F = 4x_1^2 + 2{x_1}{x_2} + 4x_2^2 - 1\) đạt giá trị nhỏ nhất. Câu 4 (3,0 điểm): Cho tam giác ABC nhọn nội tiếp đường tròn O. Các đường cao AE, BF cắt nhau tại trực tâm H của tam giác, AO cắt đường tròn tại điểm thứ hai M. a) Chứng minh tứ giác EHFC nội tiếp được đường tròn. b) Chứng minh tứ giác BHCM là hình bình hành. c) Chứng minh \(CO \bot EF\). Câu 5 (1,0 điểm): a) Giải phương trình: \(\sqrt[3]{{x - 2}} + \sqrt {x + 1} = 3\) b) Xác định đường thẳng (d): y = ax + b, biết rằng (d) đi qua điểm A(3;2), cắt trục tung tại điểm có tung độ nguyên dương, cắt trục hoành tại điểm có hoành độ là một số nguyên tố. Lời giải I. TRẮC NGHIỆM:
Câu 1 (NB): Phương pháp: Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\) Cách giải: \(P = \sqrt {16{a^2}b} \)\( = \sqrt {{{\left( {4a} \right)}^2}.b} = \left| {4a} \right|.\sqrt b = 4a\sqrt b \) (do \(a \ge 0,b \ge 0\)) Chọn A. Câu 2 (NB): Phương pháp: Đường thẳng \(\left( d \right):y = ax + b\) đi qua điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) khi \({y_A} = a{x_A} + b\). Cách giải: + Với \(x = 0\) thay vào \(y = - 2x + 1\), ta được: \(y = - 2.0 + 1 = 1\) Vậy đồ thị hàm số \(y = - 2x + 1\) đi qua điểm \(N\left( {0;1} \right)\) Chọn B. Câu 3 (NB): Phương pháp: Vận dụng kiến thức tỉ số lượng giác của góc nhọn trong tam giác vuông. Cách giải: Tam giác ABC vuông tại A, áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có: \(\tan C = \dfrac{{AB}}{{AC}}\) Chọn D. Câu 4 (NB): Phương pháp: \(\left( {{x_0},{y_0}} \right)\) là nghiệm của phương trình \(ax + by + c = 0\) nếu \(a{x_0} + b{y_0} + c = 0\) Cách giải: Thay \(x = 0;y = 0\) vào \(x + 2y - 1 = 0\), ta được: \(0 + 2.0 - 1 = 0\) (vô lí) Suy ra \(\left( {0;0} \right)\) không là nghiệm của phương trình \(x + 2y - 1 = 0\). Thay \(x = 1;y = 2\) vào \(x + 2y - 1 = 0\), ta được: \(1 + 2.2 = 1\) (vô lí) Suy ra \(\left( {1;2} \right)\) không là nghiệm của phương trình \(x + 2y - 1 = 0\). Thay \(x = 1;y = 0\) vào \(x + 2y - 1 = 0\), ta được: \(1 + 2.0 - 1 = 0\) (luôn đúng) Suy ra \(\left( {1;0} \right)\) là nghiệm của phương trình \(x + 2y - 1 = 0\). Chọn C. Câu 5 (NB): Phương pháp: Phương trình bậc hai một ẩn có dạng: \(a{x^2} + bx + c = 0\) với \(a \ne 0\) Cách giải: Phương trình bậc hai một ẩn là: \({x^2} - 2x + 3 = 0\) Chọn B. Câu 6 (NB): Phương pháp: Đồ thị hàm số \(\left( P \right):y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) khi \(\left( P \right):{y_A} = a{x_A}^2\left( {a \ne 0} \right)\) Cách giải: Thay \(x = 1;y = 2\) vào \(y = a{x^2}\), ta được: \(2 = a{.1^2} \Rightarrow a = 2\) Chọn A. Câu 7 (NB): Phương pháp: Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo cung tương ứng. Cách giải: Trong một đường tròn, nếu góc nội tiếp chắn cung có số đo \({80^0}\) thì số đo góc nội tiếp đó bằng: \({40^0}\) Chọn C. Câu 8 (NB): Phương pháp: Nếu phương trình \(a{x^2} + bx + c = 0\) với \(a \ne 0\) có hai nghiệm \({x_1}\) và \({x_2}\), thì \({x_1} + {x_2}\)\( = - \dfrac{b}{a}\) (theo định lí Vi – ét) Cách giải: Nếu phương trình \(a{x^2} + bx + c = 0\) với \(a \ne 0\) có hai nghiệm \({x_1}\) và \({x_2}\), thì \({x_1} + {x_2}\)\( = - \dfrac{b}{a}\) Chọn D. Câu 9 (NB): Phương pháp: Mặt cầu có bán kính là \(R\) thì diện tích mặt cầu được tính theo công thức: \(4\pi {R^2}\) (đơn vị diện tích) Cách giải: Mặt cầu có bán kính là \(R\) thì diện tích mặt cầu được tính theo công thức: \(4\pi {R^2}\) (đơn vị diện tích) Chọn A. Câu 10 (NB): Phương pháp: Tứ giác nội tiếp có tổng hai góc đối nhau bằng \({180^0}\). Cách giải: Tứ giác ABCD nội tiếp đường tròn (O) có \(\angle B\) và \(\angle D\) đối nhau nên \(\angle B + \angle D = {180^0}\) Chọn D.
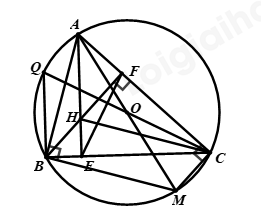
II. TỰ LUẬN Câu 1 (TH): Phương pháp: a) Biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0\) b) Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\) Sử dụng phương pháp thế, tìm được nghiệm \(y\) Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình. c) Vận dụng hệ quả của định lí Vi – ét: Nếu \(a - b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = 1;{x_2} = \dfrac{{ - c}}{a}\). Cách giải: a) Tìm điều kiện xác định của biểu thức: \(A = \sqrt {x + 1} + \sqrt {x - 2} \) ĐKXĐ: \(\left\{ \begin{array}{l}x + 1 \ge 0\\x - 2 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\x \ge 2\end{array} \right. \Leftrightarrow x \ge 2\) Vậy điều kiện xác định của biểu thức A là \(x \ge 2\) b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 3\\2x + y = 6\end{array} \right.\) \(\left\{ \begin{array}{l}x - 2y = 3\\2x + y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2y = 3\\4x + 2y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 15\\x - 2y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\3 - 2y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 0\end{array} \right.\) Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {3;0} \right)\) c) Giải phương trình: \({x^2} - 3x - 4 = 0\) Ta có: \(1 - \left( { - 3} \right) + \left( { - 4} \right) = 0\) nên phương trình có hai nghiệm phân biệt \({x_1} = - 1;{x_2} = 4\) Vậy phương trình có tập nghiệm là \(S = \left\{ { - 1;4} \right\}\) Câu 2 (TH): Phương pháp: Gọi độ dài quãng đường AB là \(x\left( {km} \right)\) (điều kiện \(x > 0\)) Thời gian xe máy đi từ A đến B và lúc đi trở về Lập phương trình, đối chiếu điều kiện và kết luận. Cách giải: Một người đi xe máy từ A đến B với vận tốc 30km/h; lúc trở về người đó đi với vận tốc 40km/h nên thời gian về ít hơn thời gian lúc đi là 30 phút. Tính quãng đường AB. Gọi độ dài quãng đường AB là \(x\left( {km} \right)\) (điều kiện \(x > 0\)) Thời gian xe máy đi từ A đến B là \(\dfrac{x}{{30}}\) (giờ) Thời gian xe máy đi trở về là \(\dfrac{x}{{40}}\) (giờ) Vì thời gian về ít hơn thời gian lúc đi là 30 phút = \(\dfrac{1}{2}\) giờ nên ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{x}{{30}} - \dfrac{x}{{40}} = \dfrac{1}{2}\\ \Leftrightarrow \left( {\dfrac{1}{{30}} - \dfrac{1}{{40}}} \right)x = \dfrac{1}{2}\end{array}\) \(\begin{array}{l} \Leftrightarrow \dfrac{x}{{120}} = \dfrac{1}{2}\\ \Rightarrow x = 60\left( {tm} \right)\end{array}\) Vậy quãng đường AB dài 60km Câu 3 (VD): Phương pháp: Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0\) (hoặc \(\Delta ' > 0\)) Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(m\) Thay vào biểu thức \(F = 4x_1^2 + 2{x_1}{x_2} + 4x_2^2 - 1\) để tìm giá trị nhỏ nhất của biểu thức. Cách giải: Cho phương trình \(2{x^2} + \left( {2m - 1} \right)x - m - 1 = 0\) với \(m\) là tham số, biết phương trình có hai nghiệm \({x_1},{x_2}\). Tìm \(m\) để biểu thức \(F = 4x_1^2 + 2{x_1}{x_2} + 4x_2^2 - 1\) đạt giá trị nhỏ nhất. Ta có: \(\Delta = {\left( {2m - 1} \right)^2} - 4.2\left( { - m - 1} \right)\)\( = 4{m^2} - 4m + 1 + 8m + 8\)\( = 4{m^2} + 4m + 9\) Để phương trình có hai nghiệm thì \(\Delta = 4{m^2} + 4m + 9 \ge 0\) \( \Leftrightarrow {\left( {2m + 1} \right)^2} + 8 \ge 0\) mọi m (luôn đúng) Do đó với mọi \(m\) phương trình luôn có hai nghiệm \({x_1},{x_2}\) Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - 2m + 1}}{2}\\{x_1}{x_2} = \dfrac{{ - m - 1}}{2}\end{array} \right.\) Ta có: \(F = 4x_1^2 + 2{x_1}{x_2} + 4x_2^2 - 1\) \( = 4\left( {x_1^2 + x_2^2} \right) + 2{x_1}{x_2} - 1\) \( = 4{\left( {{x_1} + {x_2}} \right)^2} - 8{x_1}{x_2} + 2{x_1}{x_2} - 1\) \( = 4{\left( {{x_1} + {x_2}} \right)^2} - 6{x_1}{x_2} - 1\) \(\begin{array}{l} = 4{\left( {\dfrac{{ - 2m + 1}}{2}} \right)^2} - 6\left( {\dfrac{{ - m - 1}}{2}} \right) - 1\\ = {\left( { - 2m + 1} \right)^2} - 3\left( { - m - 1} \right) - 1\end{array}\) \( = 4{m^2} - 4m + 1 - 3\left( { - m - 1} \right) - 1\) \( = 4{m^2} - m + 3\) \( = {\left( {2m} \right)^2} - 2.2m.\dfrac{1}{4} + \dfrac{1}{{16}} - \dfrac{1}{{16}} + 3\) \( = {\left( {2m - \dfrac{1}{4}} \right)^2} + \dfrac{{47}}{{16}} \ge \dfrac{{47}}{{16}}\) với mọi m (vì \({\left( {2m - \dfrac{1}{4}} \right)^2} \ge 0\) với mọi \(m\)) Do đó giá trị nhỏ nhất của \(F\) là \(\dfrac{{47}}{{16}}\) khi \(2m - \dfrac{1}{4} = 0 \Leftrightarrow 2m = \dfrac{1}{4} \Leftrightarrow m = \dfrac{1}{4}:2 = \dfrac{1}{8}\) Vậy F đạt giá trị nhỏ nhất là \(\dfrac{{47}}{{16}}\)khi \(m = \dfrac{1}{8}\). Câu 4 (VD): Phương pháp: a) Vận dụng dấu hiệu nhận biết tứ giác nội tiếp: Tứ giác có tổng hai góc đối bằng bằng 180 độ là tứ giác nội tiếp. b) Vận dụng dấu hiệu nhận biết hình bình hành: Tứ giác có các cặp cạnh đối song song với nhau là hình bình hành. c) Vận dụng kiến thức góc nội tiếp chứng minh. Cách giải: Cho tam giác ABC nhọn nội tiếp đường tròn O. Các đường cao AE, BF cắt nhau tại trực tâm H của tam giác, AO cắt đường tròn tại điểm thứ hai M.
a) Chứng minh tứ giác EHFC nội tiếp được đường tròn. Tam giác ABC có AE, BF là đường cao cắt nhau tại trực tâm H \( \Rightarrow \angle CEH = {90^0}\) và \(\angle CFH = {90^0}\) Xét tứ giác EHFC có: \(\angle CEH + \angle CFH = {90^0} + {90^0} = {180^0}\) mà hai góc này đối nhau \( \Rightarrow EHFC\) là tứ giác nội tiếp (dhnb) b) Chứng minh tứ giác BHCM là hình bình hành. Ta có C thuộc đường tròn (O) nên \(\angle ACM = {90^0}\) (góc nội tiếp chắn nửa đường tròn bằng \({90^0}\)) \( \Rightarrow MC \bot AC\) Ta có: \(\left\{ \begin{array}{l}MC \bot AC\\BH \bot AC\end{array} \right. \Rightarrow MC//BH\) (quan hệ từ vuông góc đến song song) Ta có B thuộc đường tròn (O) nên \(\angle ABM = {90^0}\) (góc nội tiếp chắn nửa đường tròn bằng \({90^0}\)) \( \Rightarrow AB \bot BM\) Ta có: \(\left\{ \begin{array}{l}CH \bot AB\\BM \bot AB\end{array} \right. \Rightarrow CH//BM\) (quan hệ từ vuông góc đến song song) Tứ giác BHCM có: \(\left\{ \begin{array}{l}MC//BH\\CH//BM\end{array} \right.\) \( \Rightarrow BHCM\) là hình bình hành (dhnb) c) Chứng minh \(CO \bot EF\). Kéo dài OC cắt đường tròn (O) tại Q nên CQ là đường trình của đường tròn (O) Tứ giác AFEB có \(\angle AEB = \angle AFB = {90^0}\) mà hai góc này có đỉnh kề nhau Suy ra AFEB là tứ giác nội tiếp (dhnb) \( \Rightarrow \angle BAF = \angle FEC\) (cùng bù với \(\angle BEF\)) Tứ giác EHFC nội tiếp đường tròn (cmt) nên \(\angle FHO = \angle FEC\) (2 góc nội tiếp cùng chắn cung CF) Suy ra \(\angle BAF = \angle FEC\) hay \(\angle BAC = \angle FEC\) Xét (O) có: \(\angle BQC = \angle BAC\) (hai góc nội tiếp cùng chắn cung BC) Suy ra \(\angle FEC = \angle BAC\) Có B thuộc đường tròn tâm O đường kính QC \( \Rightarrow \angle QBC = {90^0}\) (góc nội tiếp chắn nửa đường tròn) Ta có: \(\angle BQC + \angle QCB = \angle QBC = {90^0}\) \(\begin{array}{l} \Rightarrow \angle FEC + \angle QCB = {90^0}\\ \Rightarrow CQ \bot EF\,\,hay\,\,CO \bot EF\end{array}\) Câu 5 (VDC): Phương pháp: a) Sử dụng phương pháp nhân liên hợp tìm nhân tử chung để giải phương trình tìm x. b) Lập phương trình đường thẳng, lập luận tìm các giá trị. Cách giải: a) Giải phương trình: \(\sqrt[3]{{x - 2}} + \sqrt {x + 1} = 3\) ĐKXĐ: \(x \ge - 1\) \(\begin{array}{l}\,\,\,\,\,\,\,\,\sqrt[3]{{x - 2}} + \sqrt {x + 1} = 3\\ \Leftrightarrow \sqrt[3]{{x - 2}} - 1 + \sqrt {x + 1} - 2 = 0\\ \Leftrightarrow \dfrac{{{{\left( {\sqrt[3]{{x - 2}}} \right)}^3} - {1^3}}}{{{{\left( {\sqrt[3]{{x - 2}}} \right)}^2} + \sqrt[3]{{x - 2}} + 1}} + \dfrac{{{{\left( {\sqrt {x + 1} } \right)}^2} - {2^2}}}{{\sqrt {x + 1} + 2}} = 0\\ \Leftrightarrow \dfrac{{x - 3}}{{{{\left( {\sqrt[3]{{x - 2}}} \right)}^2} + \sqrt[3]{{x - 2}} + 1}} + \dfrac{{x - 3}}{{\sqrt {x + 1} + 2}} = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {\dfrac{1}{{{{\left( {\sqrt[3]{{x - 2}}} \right)}^2} + \sqrt[3]{{x - 2}} + 1}} + \dfrac{1}{{\sqrt {x + 1} + 2}}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\\dfrac{1}{{{{\left( {\sqrt[3]{{x - 2}}} \right)}^2} + \sqrt[3]{{x - 2}} + 1}} + \dfrac{1}{{\sqrt {x + 1} + 2}} = 0\,\,\,\,\left( * \right)\end{array} \right.\end{array}\) Xét phương trình (*): \(\dfrac{1}{{{{\left( {\sqrt[3]{{x - 2}}} \right)}^2} + \sqrt[3]{{x - 2}} + 1}} + \dfrac{1}{{\sqrt {x + 1} + 2}} = 0\) *Vì \({\left( {\sqrt[3]{{x - 2}}} \right)^2} + \sqrt[3]{{x - 2}} + 1 = {\left( {\sqrt[3]{{x - 2}}} \right)^2} + 2.\dfrac{1}{2}.\sqrt[3]{{x - 2}} + \dfrac{1}{4} - \dfrac{1}{4} + 1 = {\left( {\sqrt[3]{{x - 2}} + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \ge \dfrac{3}{4},\forall x\) Do đó, \({\left( {\sqrt[3]{{x - 2}}} \right)^2} + \sqrt[3]{{x - 2}} + 1 > 0\), mọi x Suy ra \(\dfrac{1}{{{{\left( {\sqrt[3]{{x - 2}}} \right)}^2} + \sqrt[3]{{x - 2}} + 1}} > 0\) *Vì \(x \ge - 1 \Rightarrow \sqrt {x + 1} > 0 \Rightarrow \sqrt {x + 1} + 2 \ge 2\) Suy ra \(\dfrac{1}{{\sqrt {x + 1} + 2}} > 0\) Do đó, \(\dfrac{1}{{{{\left( {\sqrt[3]{{x - 2}}} \right)}^2} + \sqrt[3]{{x - 2}} + 1}} + \dfrac{1}{{\sqrt {x + 1} + 2}} > 0\) Suy ra phương trình (*) vô nghiệm Vậy phương trình có nghiệm duy nhất \(x = 3\). b) Xác định đường thẳng (d): y = ax + b, biết rằng (d) đi qua điểm A(3;2), cắt trục tung tại điểm có tung độ nguyên dương, cắt trục hoành tại điểm có hoành độ là một số nguyên tố. Đường thẳng \(\left( d \right):y = ax + b\) đi qua điểm A(3;2) nên ta có: \(2 = 3a + b\) (1) Đường thẳng (d) cắt Oy tại điểm có tung độ nguyên dương nên \(\left\{ \begin{array}{l}y = ax + b\\x = 0\end{array} \right. \Rightarrow y = b\) với \(b \in {\mathbb{Z}^ + }\) Đường thẳng (d) cắt trục Ox tại điểm có hoành độ là một số nguyên tố nên \(ax + b = 0 \Rightarrow x = - \dfrac{b}{a} \Leftrightarrow b = - ax\), với x là số nguyên tố. Thay vào (1) ta có: \(2 = 3a - ax \Leftrightarrow a\left( {3 - x} \right) = 2\) Ta có bảng sau:
Vì x là số nguyên tố nên \(x \in \left\{ {2;5} \right\}\) *Với \(a = - 1;x = 5 \Rightarrow b = - \left( { - 1} \right).5 = 5\left( {tm} \right)\) Khi đó phương trình đường thẳng \(\left( d \right):y = - x + 5\) *Với \(a = 2;x = 2 \Rightarrow b = - 2.2 = - 4 < 0\) nên không thỏa mãn điều kiện. Vậy phương trình đường thẳng \(\left( d \right):y = - x + 5\).
|




















Danh sách bình luận