Đề số 36 - Đề thi vào lớp 10 môn Toán

Đề bài

Câu 1 (2 điểm):

a) Tìm \(x\) để biểu thức sau có nghĩa: \(P = \sqrt {5x + 3}  + 2018\sqrt[3]{x}.\)

b) Cho hàm số \(y = \dfrac{1}{2}{x^2}.\) Điểm \(D\) có hoành độ \(x =  - 2\) thuộc đồ thị hàm số. Tìm tọa độ điểm \(D.\)

c) Tìm giá trị của \(a\) và \(b\) để đường thẳng \(d:\;\;y = ax + b - 1\) đi qua hai điểm \(A\left( {1;\;1} \right)\) và \(B\left( {2;\;3} \right).\)

Câu 2 (2,0 điểm):

Cho biểu thức: \(P = \dfrac{{x\sqrt y  + y\sqrt x }}{{\sqrt {xy} }} - \dfrac{{{{\left( {\sqrt x  + \sqrt y } \right)}^2} - 4\sqrt {xy} }}{{\sqrt x  - \sqrt y }} - y\) (với \(x > 0,\;\;y > 0,\;\;x \ne y\)).

a) Rút gọn biểu thức \(P.\)               

b) Chứng minh rằng \(P \le 1.\)

Câu 3 (2,0 điểm):

Cho phương trình \({x^2} - 4mx + 4{m^2} - 2 = 0\;\;\;\left( 1 \right)\)

a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1.\)

b) Chứng minh rằng với mọi \(m\) phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt.

Giả sử hai nghiệm là \({x_1},\;{x_2}\) khi đó tìm \(m\) để \(x_1^2 + 4m{x_2} + 4{m^2} - 6 = 0.\)

Câu 4 (3,5 điểm):

Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Tiếp tuyến của đường tròn tâm O tại điểm C cắt các đường thẳng AB và AD  theo thứ tự tại M, N. Dựng AH  vuông góc với BD tại điểm H,  K  là giao điểm của hai đường thẳng MN  và BD.

a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.

b) Chứng minh AD.AN = AB.AM.

c) Gọi E  là trung điểm của MN. Chứng minh ba điểm A, H, E thẳng hàng.

d) Cho AB = 6cm, AD = 8cm. Tính độ dài đoạn MN.

Câu 5 (0,5 điểm): Giải phương trình: \(3\sqrt 3 \left( {{x^2} + 4x + 2} \right) - \sqrt {x + 8}  = 0.\)

Lời giải chi tiết

Câu 1:

a) Tìm \(x\) để biểu thức sau có nghĩa: \(P = \sqrt {5x + 3}  + 2018\sqrt[3]{x}.\)

Biểu thức có nghĩa \( \Leftrightarrow 5x + 3 \ge 0 \Leftrightarrow x \ge  - \dfrac{3}{5}.\)

Vậy với \(x \ge  - \dfrac{3}{5}\) thì biểu thức \(P\) có nghĩa.

b) Cho hàm số \(y = \dfrac{1}{2}{x^2}.\) Điểm \(D\) có hoành độ \(x =  - 2\) thuộc đồ thị hàm số. Tìm tọa độ điểm \(D.\)

Điểm \(D\) thuộc đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\) và có hoành độ \(x =  - 2 \Rightarrow y = \dfrac{1}{2}.{\left( { - 2} \right)^2} = 2.\)

Vậy \(D\left( { - 2;\;2} \right).\)

c) Tìm giá trị của \(a\) và \(b\) để đường thẳng \(d:\;\;y = ax + b - 1\) đi qua hai điểm \(A\left( {1;\;1} \right)\) và \(B\left( {2;\;3} \right).\)

Đường thẳng \(d\) đi qua hai điểm \(A\left( {1;\;1} \right)\) và \(B\left( {2;\;3} \right)\) nên ta có:

\(\left\{ \begin{array}{l}1 = 1.a + b - 1\\3 = 2.a + b - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + b = 2\\2a + b = 4\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 0\end{array} \right..\)

Vậy \(a = 2\) và \(b = 0.\)

Câu 2:

Cho biểu thức: \(P = \dfrac{{x\sqrt y  + y\sqrt x }}{{\sqrt {xy} }} - \dfrac{{{{\left( {\sqrt x  + \sqrt y } \right)}^2} - 4\sqrt {xy} }}{{\sqrt x  - \sqrt y }} - y\) (với \(x > 0,\;\;y > 0,\;\;x \ne y\)).

a) Rút gọn biểu thức \(P.\)

Điều kiện: \(x > 0,\;\;y > 0,\;\;x \ne y.\)

\(\begin{array}{l}P = \dfrac{{x\sqrt y  + y\sqrt x }}{{\sqrt {xy} }} - \dfrac{{{{\left( {\sqrt x  + \sqrt y } \right)}^2} - 4\sqrt {xy} }}{{\sqrt x  - \sqrt y }} - y\\\;\;\; = \dfrac{{\sqrt {xy} \left( {\sqrt x  + \sqrt y } \right)}}{{\sqrt {xy} }} - \dfrac{{x + 2\sqrt {xy}  + y - 4\sqrt {xy} }}{{\sqrt x  - \sqrt y }} - y\\\;\;\; = \sqrt x  + \sqrt y  - \dfrac{{{{\left( {\sqrt x  - \sqrt y } \right)}^2}}}{{\sqrt x  - \sqrt y }} - y\\\;\;\; = \sqrt x  + \sqrt y  - \left( {\sqrt x  - \sqrt y } \right) - y\\\;\;\; = \sqrt x  + \sqrt y  - \sqrt x  + \sqrt y  - y\\\;\;\; = 2\sqrt y  - y.\end{array}\)

b) Chứng minh rằng \(P \le 1.\)

Ta có: \(P \le 1\)

\(\begin{array}{l} \Leftrightarrow 2\sqrt y  - y \le 1\\ \Leftrightarrow 1 - 2\sqrt y  + y \ge 0\\ \Leftrightarrow {\left( {\sqrt y  - 1} \right)^2} \ge 0\;\;\forall y > 0.\end{array}\)

Vậy \(P \le 1.\)

Câu 3:

Cho phương trình \({x^2} - 4mx + 4{m^2} - 2 = 0\;\;\;\left( 1 \right)\)

a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1.\)

Với \(m = 1\) ta có phương trình:

\(\begin{array}{l}\left( 1 \right) \Leftrightarrow {x^2} - 4x + 4 - 2 = 0\\ \Leftrightarrow {x^2} - 4x + 2 = 0\end{array}\)

Có \(\Delta ' = 4 - 2 = 2 > 0\)

\( \Rightarrow \) Phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 2 + \sqrt 2 \\{x_2} = 2 - \sqrt 2 \end{array} \right..\)

Vậy với \(m = 1\) thì phương trình có tập nghiệm \(S = \left\{ {2 - \sqrt 2 ;\;\;2 + \sqrt 2 } \right\}.\)

b) Chứng minh rằng với mọi \(m\) phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt.

Giả sử hai nghiệm là \({x_1},\;{x_2}\) khi đó tìm \(m\) để \(x_1^2 + 4m{x_2} + 4{m^2} - 6 = 0.\)

Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)

\( \Leftrightarrow 4{m^2} - 4{m^2} + 2 > 0 \Leftrightarrow 2 > 0\) (luôn đúng với mọi \(m\))

Vậy phương trình luôn có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) với mọi \(m.\)

Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4m\\{x_1}{x_2} = 4{m^2} - 2\end{array} \right..\)

Vì \({x_1}\) là nghiệm của phương trình \(\left( 1 \right)\)

\(\Rightarrow x_1^2 - 4m{x_1} + 4{m^2} - 2 = 0\)

\(\Leftrightarrow x_1^2 = 4m{x_1} - 4{m^2} + 2.\;\)

Theo đề bài ta có: \(x_1^2 + 4m{x_2} + 4{m^2} - 6 = 0\)

\(\begin{array}{l} \Leftrightarrow 4m{x_1} - 4{m^2} + 2 + 4m{x_2} + 4{m^2} - 6 = 0\\ \Leftrightarrow 4m\left( {{x_1} + {x_2}} \right) - 4 = 0\\ \Leftrightarrow m\left( {{x_1} + {x_2}} \right) = 1\\ \Leftrightarrow m.4m = 1\\ \Leftrightarrow {m^2} = \dfrac{1}{4}\\ \Leftrightarrow m =  \pm \dfrac{1}{2}.\end{array}\)

Vậy \(m =  \pm \dfrac{1}{2}\) thỏa mãn yêu cầu bài toán.

Câu 4:

a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Tiếp tuyến của đường tròn tâm O tại điểm C cắt các đường thẳng AB và AD  theo thứ tự tại M, N. Dựng AH  vuông góc với BD tại điểm H,  K  là giao điểm của hai đường thẳng MN  và BD.

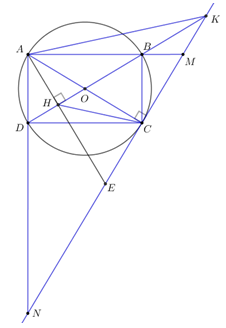
Xét tứ giác \(AHCK\) ta có: \(\widehat {AHK} = \widehat {ACK} = {90^0}\)

Mà hai đỉnh \(H,\;C\) kề nhau cùng nhìn cạnh \(AK\) dưới góc \({90^0}.\)

\( \Rightarrow AHCK\)  là tứ giác nội tiếp. (dhnb)

b) Chứng minh AD.AN = AB.AM.

Ta có: \(AM//CD \Rightarrow \widehat {AMN} = \widehat {DCN}\) (hai góc đồng vị)

\(\widehat {DCN}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung \(CD.\)

\(\widehat {ADB}\) là góc nội tiếp chắn cung \(AB.\)

Mà cung \(AB = \) cung \(CD\) do \(ABCD\) là hình chữ nhật.

\( \Rightarrow \widehat {ADB} = \widehat {AMN}\left( { = \widehat {DCN}} \right).\)

Xét \(\Delta ABD\) và \(\Delta ANM\) ta có:

\(\begin{array}{l}\widehat {A\;\;}\;\;chung\\\widehat {ADB} = \widehat {AMN}\;\;\left( {cmt} \right)\\ \Rightarrow \Delta ABD \sim \Delta ANM\;\;\left( {g - g} \right)\\ \Rightarrow \dfrac{{AB}}{{AN}} = \dfrac{{AD}}{{AM}} \Rightarrow AB.AM = AD.AN\;\;\left( {dpcm} \right).\end{array}\)

c) Gọi E  là trung điểm của MN. Chứng minh ba điểm A, H, E thẳng hàng.

Ta có \(E\) là trung điểm của \(MN\;\;\left( {gt} \right) \Rightarrow AE = ME = EN\) (tính chất đường trung tuyến ứng với cạnh huyền)

\( \Rightarrow \widehat {EAN} = \widehat {ENA}\)

\(\Rightarrow \widehat {AEM} = \widehat {EAN} + \widehat {ANE} = 2\widehat {ENA}\) (góc ngoài của tam giác).

Vì \(\Delta ABD \sim \Delta ANM\;\left( {cmt} \right) \Rightarrow \widehat {ABD} = \widehat {ANC}\) (hai góc tương ứng).

Vì \(ABCD\) là hình chữ nhật \( \Rightarrow \widehat {ABD} = \widehat {BDC}\) (hai góc so le trong).

\( \Rightarrow \widehat {BDC} = \widehat {ANC}\left( { = \widehat {ABD}} \right) \\\Rightarrow \widehat {HEC} = 2\widehat {ANE} = 2\widehat {BDC} = 2\widehat {ODC}.\;\;\;\left( 1 \right)\)

Xét \(\Delta OCD\) cân tại \(O\) ta có: \(\widehat {DOC} + \widehat {OCD} + \widehat {ODC} = {180^0} \)

\(\Leftrightarrow \widehat {DOC} + 2.\widehat {ODC} = {180^0}.\;\;\;\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow \widehat {DOC} + \widehat {HEC} = {180^0}.\)

Xét tứ giác \(OHEC\) ta có: \(\widehat {DOC} + \widehat {HEC} = {180^0}\;\;\left( {cmt} \right)\)

\( \Rightarrow OHEC\) là tứ giác nội tiếp (tổng hai góc đối diện có tổng bằng \({180^0}\)).

\(\begin{array}{l} \Rightarrow \widehat {OHE} + \widehat {OCE} = {180^0} \\\Leftrightarrow \widehat {OHE} = {180^0} - {90^0} = {90^0}\\ \Rightarrow OH \bot HE.\end{array}\)

Mà \(OE \bot AH\;\;\;\left( {gt} \right)\)

\( \Rightarrow A,\;H,\;E\) thẳng hàng.

d) Cho AB = 6cm, AD = 8cm. Tính độ dài đoạn MN.

Áp dụng định lý Pi-ta-go cho tam giác \(ABC\) vuông tại \(A\) ta có:

\(D{B^2} = A{B^2} + A{D^2} = {6^2} + {8^2} = {10^2} \Rightarrow BD = 10cm.\)

Vì \(\Delta ABD \sim \Delta ANM\;\left( {cmt} \right)\)

\(\Rightarrow \dfrac{{AB}}{{AN}} = \dfrac{{BD}}{{MN}} = \dfrac{{AD}}{{AM}}\)

\( \Leftrightarrow \dfrac{6}{{AN}} = \dfrac{8}{{AM}} = \dfrac{{10}}{{MN}}\\ \Leftrightarrow \left\{ \begin{array}{l}AM = \dfrac{{8MN}}{{10}} = \dfrac{4}{5}MN\\AN = \dfrac{6}{{10}}MN = \dfrac{3}{5}MN\end{array} \right..\)

Xét tam giác \(\Delta DBC\) và \(\Delta CMB\) ta có:

\(\widehat {DCB} = \widehat {CBM} = {90^0}\)

\(\widehat {BDC} = \widehat {BCM}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(BC\))

\(\begin{array}{l} \Rightarrow \Delta DCB \sim CBM\left( {g - g} \right)\\ \Rightarrow \dfrac{{DC}}{{BC}} = \dfrac{{BC}}{{BM}} \Leftrightarrow \dfrac{6}{8} = \dfrac{8}{{BM}}\\ \Leftrightarrow BM = \dfrac{{32}}{3}\;cm.\\ \Rightarrow AM = AB + BM = 6 + \dfrac{{32}}{3} = \dfrac{{50}}{3}\;cm.\\ \Rightarrow MN = \dfrac{5}{4}AM = \dfrac{5}{4}.\dfrac{{50}}{3} = \dfrac{{125}}{6}cm.\end{array}\)

Vậy \(MN = \dfrac{{125}}{6}cm.\)

 Loigiaihay.com