Đề số 37 - Đề thi vào lớp 10 môn Toán

Đề bài

Câu 1 (1 điểm): Không dùng máy tính cầm tay, hãy giải phương trình: \(\left( {x - 2018} \right)\left( {x - 2020} \right) = 2018 - x.\)

Câu 2 (1 điểm): Không dùng máy tính cầm tay, tính giá trị biểu thức: \(A = \dfrac{{\sqrt {15}  - \sqrt {12} }}{{\sqrt 5  - 2}} - \dfrac{1}{{2 - \sqrt 3 }}.\)

Câu 3 (1 điểm): Rút gọn biểu thức: \(P = \left( {\dfrac{{3\sqrt x }}{{\sqrt x  + 2}} + \dfrac{{\sqrt x }}{{\sqrt x  - 2}} - \dfrac{{x - \sqrt x }}{{x - 4}}} \right):\dfrac{{3\sqrt x }}{{\sqrt x  + 2}}\)  với \(x > 0,\;\;x \ne 4.\) 

Câu 4 (1 điểm): Cho hàm số bậc nhất \(y = mx + 1\) với \(m\) là tham số. Tìm \(m\) để đồ thị hàm số đi qua điểm \(A\left( {1;\;4} \right).\)  Với giá trị \(m\) vừa tìm được, hàm số đồng biến hay nghịch biến trên \(R.\)

Câu 5 (1 điểm): Giải hệ phương trình: \(\left\{ \begin{array}{l}3\left( {x + 1} \right) + 2\left( {x + 2y} \right) = 4\\4\left( {x + 1} \right) - \left( {x + 2y} \right) = 9\end{array} \right..\)

Câu 6 (1 điểm): Cho phương trình \({x^2} - 4x + 4m - 3 = 0\) với \(m\) là tham số. Tìm giá trị của \(m\) để phương trình có hai nghiệm \({x_1};\;{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 14.\)

Câu 7 (1 điểm): Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH,\) biết \(AC = 16cm\) và \(\sin \widehat {CAH} = \dfrac{4}{5}.\) Tính độ dài các cạnh \(BC,\;AB.\)

Câu 8 (1 điểm): Cho hai đường tròn \(\left( {O;\;4cm} \right)\) và \(\left( {O';\;11cm} \right).\) Biết khoảng cách \(OO' = 2a + 3\;\left( {cm} \right)\) với \(a\) là số thực dương. Tìm \(a\) để hai đường tròn tiếp xúc nhau.

Câu 9 (1 điểm): Cho đường tròn tâm O, dây cung AB không đi qua tâm O. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây cung MC không đi qua tâm O cắt đoạn thẳng AB tại D (D khác A, D khác B). Đường thẳng vuông góc với AB tại D, cắt OC tại K.Chứng minh rằng tam giác KCD là tam giác đều.

Câu 10 (1 điểm): Cho tam giác ABC có ba góc nhọn và AB < AC nội tiếp đường tròn tâm O. Các đường cao BE, CF của tam giác ABC cắt nhau tại H.

a) Chứng minh tứ giác AFHE nội tiếp được trong một đường tròn. Xác định tâm và bán kính của đường tròn đó.

b) Gọi M là giao điểm của EF và BC, đường thẳng MA cắt (O) tại điểm thứ hai là I khác A. Chứng minh tứ giác AEFI nội tiếp được một đường tròn.

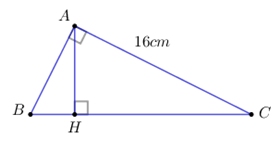
Lời giải chi tiết

Câu 1:

Không dùng máy tính cầm tay, hãy giải phương trình: \(\left( {x - 2018} \right)\left( {x - 2020} \right) = 2018 - x.\)

Ta có: \(\left( {x - 2018} \right)\left( {x - 2020} \right) = 2018 - x\)

\(\begin{array}{l} \Leftrightarrow \left( {x - 2018} \right)\left( {x - 2020} \right) + x - 2018 = 0\\ \Leftrightarrow \left( {x - 2018} \right)\left( {x - 2020 + 1} \right) = 0\\ \Leftrightarrow \left( {x - 2018} \right)\left( {x - 2019} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2018 = 0\\x - 2019 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2018\\x = 2019\end{array} \right..\end{array}\)

Vậy phương trình có tập nghiệm \(S = \left\{ {2018;\;2019} \right\}.\)

Câu 2:

Không dùng máy tính cầm tay, tính giá trị biểu thức: \(A = \dfrac{{\sqrt {15}  - \sqrt {12} }}{{\sqrt 5  - 2}} - \dfrac{1}{{2 - \sqrt 3 }}.\)

\(\begin{array}{l}A = \dfrac{{\sqrt {15}  - \sqrt {12} }}{{\sqrt 5  - 2}} - \dfrac{1}{{2 - \sqrt 3 }}\\\;\;\; = \dfrac{{\sqrt {3.5}  - 2\sqrt 3 }}{{\sqrt 5  - 2}} - \dfrac{{2 + \sqrt 3 }}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}}\\\;\;\; = \dfrac{{\sqrt 3 \left( {\sqrt 5  - 2} \right)}}{{\sqrt 5  - 2}} - \dfrac{{2 + \sqrt 3 }}{{4 - 3}} \\\;\;\;= \sqrt 3  - 2 - \sqrt 3  =  - 2.\end{array}\)

Vậy \(A =  - 2.\)

Câu 3:

Rút gọn biểu thức: \(P = \left( {\dfrac{{3\sqrt x }}{{\sqrt x  + 2}} + \dfrac{{\sqrt x }}{{\sqrt x  - 2}} - \dfrac{{x - \sqrt x }}{{x - 4}}} \right):\dfrac{{3\sqrt x }}{{\sqrt x  + 2}}\)  với \(x > 0,\;\;x \ne 4.\) 

Điều kiện: \(x > 0,\;\;x \ne 4.\)

\(\begin{array}{l}P = \left( {\dfrac{{3\sqrt x }}{{\sqrt x  + 2}} + \dfrac{{\sqrt x }}{{\sqrt x  - 2}} - \dfrac{{x - \sqrt x }}{{x - 4}}} \right):\dfrac{{3\sqrt x }}{{\sqrt x  + 2}}\\\;\;\; = \left( {\dfrac{{3\sqrt x }}{{\sqrt x  + 2}} + \dfrac{{\sqrt x }}{{\sqrt x  - 2}} - \dfrac{{x - \sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}} \right):\dfrac{{3\sqrt x }}{{\sqrt x  + 2}}\\\;\;\; = \dfrac{{3\sqrt x \left( {\sqrt x  - 2} \right) + \sqrt x \left( {\sqrt x  + 2} \right) - x + \sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}:\dfrac{{3\sqrt x }}{{\sqrt x  + 2}}\\\;\;\; = \dfrac{{3x - 6\sqrt x  + x + 2\sqrt x  - x + \sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}.\dfrac{{\sqrt x  + 2}}{{3\sqrt x }}\\\;\;\; = \dfrac{{3x - 3\sqrt x }}{{\sqrt x  - 2}}.\dfrac{1}{{3\sqrt x }} = \dfrac{{3\sqrt x \left( {\sqrt x  - 1} \right)}}{{3\sqrt x \left( {\sqrt x  - 2} \right)}} = \dfrac{{\sqrt x  - 1}}{{\sqrt x  - 2}}.\end{array}\)

Câu 4:

Cho hàm số bậc nhất \(y = mx + 1\) với \(m\) là tham số. Tìm \(m\) để đồ thị hàm số đi qua điểm \(A\left( {1;\;4} \right).\)  Với giá trị \(m\) vừa tìm được, hàm số đồng biến hay nghịch biến trên \(R.\)

Hàm số \(y = mx + 1\) là hàm số bậc nhất khi \(m \ne 0\)

Đồ thị hàm số đi qua điểm \(A\left( {1;\;4} \right) \Rightarrow 4 = m.1 + 1 \Leftrightarrow m = 3.\left( {tm} \right)\)

Khi đó hàm số có dạng: \(y = 3x + 1.\)

Hàm số có \(a = 3 > 0\) nên hàm số đồng biến trên \(R.\)

Câu 5:

Giải hệ phương trình: \(\left\{ \begin{array}{l}3\left( {x + 1} \right) + 2\left( {x + 2y} \right) = 4\\4\left( {x + 1} \right) - \left( {x + 2y} \right) = 9\end{array} \right..\)

\(\begin{array}{l}\left\{ \begin{array}{l}3\left( {x + 1} \right) + 2\left( {x + 2y} \right) = 4\\4\left( {x + 1} \right) - \left( {x + 2y} \right) = 9\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}3x + 3 + 2x + 4y = 4\\4x + 4 - x - 2y = 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}5x + 4y = 1\\3x - 2y = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}5x + 4y = 1\\6x - 4y = 10\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}11x = 11\\2y = 3x - 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\2y = 3 - 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\2y =  - 2\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 1\end{array} \right..\end{array}\)

Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\;y} \right) = \left( {1;\; - 1} \right).\)

Câu 6:

Cho phương trình \({x^2} - 4x + 4m - 3 = 0\) với \(m\) là tham số. Tìm giá trị của \(m\) để phương trình có hai nghiệm \({x_1};\;{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 14.\)

 Phương trình đã cho có hai nghiệm \({x_1},\;{x_2} \Leftrightarrow \Delta ' \ge 0\)

\(\begin{array}{l} \Leftrightarrow 4 - 4m + 3 \ge 0\\ \Leftrightarrow 4m \le 7\\ \Leftrightarrow m \le \dfrac{7}{4}.\end{array}\)

Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}{x_2} = 4m - 3\end{array} \right..\)

Theo đề bài ta có: \(x_1^2 + x_2^2 = 14\)

\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 14\\ \Leftrightarrow {4^2} - 2\left( {4m - 3} \right) = 14\\ \Leftrightarrow 16 - 8m + 6 = 14\\ \Leftrightarrow 8m = 8\\ \Leftrightarrow m = 1\;\;\left( {tm} \right).\end{array}\)

Vậy \(m = 1.\)

Câu 7:

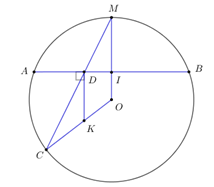
Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH,\) biết \(AC = 16cm\) và \(\sin \widehat {CAH} = \dfrac{4}{5}.\) Tính độ dài các cạnh \(BC,\;AB.\)

Xét tam giác \(CAH\) vuông tại \(H\) ta có:

\(\sin \widehat {CAH} = \dfrac{4}{5} \)

\(\Leftrightarrow \dfrac{{HC}}{{AC}} = \dfrac{{HC}}{{16}} = \dfrac{4}{5} \)

\(\Leftrightarrow HC = \dfrac{{4.16}}{5} = 12,8cm.\)

Áp dụng hệ thức lượng cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH\) ta có:

\(A{C^2} = HC.BC \)

\(\Rightarrow BC = \dfrac{{A{C^2}}}{{HC}} = \dfrac{{{{16}^2}}}{{12,8}} = 20\left( {cm} \right)\)

Áp dụng định lý Pi-ta-go trong tam giác vuông ABC ta có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} \\\Rightarrow A{B^2} = B{C^2} - A{C^2} = {20^2} - {16^2} = 144\\ \Rightarrow AB = 12\left( {cm} \right)\end{array}\)

Vậy BC = 20 cm; AB = 12 cm.

Câu 8:

Cho hai đường tròn \(\left( {O;\;4cm} \right)\) và \(\left( {O';\;11cm} \right).\) Biết khoảng cách \(OO' = 2a + 3\;\left( {cm} \right)\) với \(a\) là số thực dương. Tìm \(a\) để hai đường tròn tiếp xúc nhau.

Hai đường tròn tiếp xúc ngoài nhau nếu: \(OO' = 4 + 11 = 15 \Rightarrow 2a + 3 = 15 \Leftrightarrow a = 6\;\;\left( {tm} \right).\)

Hai đường tròn tiếp xúc trong nhau nếu: \(OO' = \left| {4 - 11} \right| = 7 \Rightarrow 2a + 3 = 7 \Leftrightarrow a = 2\;\;\left( {tm} \right).\)

Vậy \(a = 2\) hoặc \(a = 6\) thỏa mãn bài toán.

Câu 9:

Cho đường tròn tâm O, dây cung AB không đi qua tâm O. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây cung MC không đi qua tâm O cắt đoạn thẳng AB tại D (D khác A, D khác B). Đường thẳng vuông góc với AB tại D, cắt OC tại K.Chứng minh rằng tam giác KCD là tam giác đều.

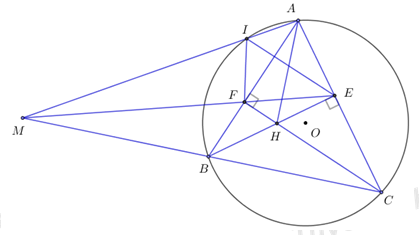
Nên ta có OM là đường trung trực của \(AB\;\;hay\;\;AB \bot OM.\)Ta có \(M\) là điểm chính giữa cung AB, suy ra cung  MA bằng cung MB, suy ra MA = MB (trong một đường tròn thì hai cung căng hai dây bằng nhau); Lại có OA = OB (bán kính của (O))

Lại có \(KD \bot AB\;\;\left( {gt} \right)\)

\( \Rightarrow KD//OM\) (từ vuông góc đến song song).

\( \Rightarrow \widehat {CMO} = \widehat {CDK}\) (hai góc đồng vị).

Ta có \(OC = OM = R \Rightarrow \Delta MOC\) cân tại O \( \Rightarrow \widehat {OMC} = \widehat {OCM}.\) (hai góc kề đáy).

\( \Rightarrow \widehat {MCO} = \widehat {CDK}\left( { = \widehat {CMO}} \right) \Rightarrow \Delta KCD\) cân tại \(K.\)  (đpcm).

Câu 10:

Cho tam giác ABC có ba góc nhọn và AB < AC nội tiếp đường tròn tâm O. Các đường cao BE, CF của tam giác ABC cắt nhau tại H.

a) Chứng minh tứ giác AFHE nội tiếp được trong một đường tròn. Xác định tâm và bán kính của đường tròn đó.

Ta có \(\Delta AFH\) vuông tại \(F\left( {do\,\,CF \bot AB} \right) \Rightarrow A,\;F,\;H\) cùng thuộc đường tròn đường kính \(AH.\)    (1)

\(\Delta AEH\) vuông tại \(E\left( {do\,\,BE \bot AC} \right) \Rightarrow A,\;E,\;H\) cùng thuộc đường tròn đường kính \(AH.\)    (2)

Từ (1) và (2) ta có 4 điểm \(A,\;E,\;F,\;H\) cùng thuộc đường tròn tâm là trung điểm của \(AH\) và bán kính \(R = \dfrac{{AH}}{2}.\)

Hay tứ giác \(AEHF\) nội tiếp đường tròn tâm là trung điểm của \(AH\) và bán kính \(R = \dfrac{{AH}}{2}.\)

 Loigiaihay.com