Đề thi vào 10 môn Toán Hải Phòng năm 2021

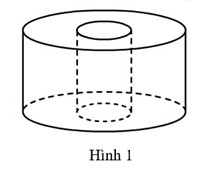
Đề bài

Câu 1. (1,5 điểm)

Cho hai biểu thức: \(A = \sqrt {50}  - 3\sqrt 8  + \sqrt {{{\left( {\sqrt 2  + 1} \right)}^2}} ;\)\(B = \dfrac{{x\sqrt x  - \sqrt x }}{{x - 1}} + \dfrac{{x - 1}}{{\sqrt x  + 1}}\) (với \(x \ge 0,\,\,x \ne 1\)).

a) Rút gọn các biểu thức \(A,\,\,B.\)

b) Tìm các giá trị của \(x\) sao cho \(A \le B.\)

Câu 2. (1,5 điểm)

1) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + \dfrac{1}{{\sqrt y }} = 3\\x - \dfrac{1}{{\sqrt y }} = 0\end{array} \right. \cdot \)

2) Bạn Nam hiện có \(50\,000\) đồng. Để phục vụ cho việc học tập, bạn muốn mua một quyển sách tham khảo Toán có giá \(150\,000\) đồng. Vì thế, bạn Nam đã lên kế hoạch mỗi ngày tiết kiệm \(5\,000\) đồng. Gọi số tiền bạn Nam tiết kiệm được sau \(x\) (ngày) (gồm cả tiền hiện có và tiền tiết kiệm được hàng ngày) là \(y\) (đồng).

a) Lập công thức tính \(y\) theo \(x\).

b) Hỏi sau bao nhiêu ngày bạn Nam có vừa đủ tiền để mua được quyển sách tham khảo Toán?

Câu 3. (2,5 điểm)

1) Cho phương trình \({x^2} - 2(m + 1)x + {m^2} + 2 = 0\)\(\left( 1 \right)\) (\(x\) là ẩn số, \(m\) là tham số).

a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1.\)

b) Xác định các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn điều kiện \(x_1^2 + 2\left( {m + 1} \right){x_2} = 12m + 2\).

2) Bài toán có nội dung thực tế:

 Lúc \(9\) giờ sáng, một xe ô tô khởi hành từ \(A\) đến \(B\) với vận tốc không đổi trên cả quãng đường là \(55\,\)km/h. Sau khi xe ô tô này đi được \(20\)phút thì cũng trên quãng đường đó, một xe ô tô khác bắt đầu đi từ \(B\) về \(A\) với vận tốc không đổi trên cả quãng đường là \(45\)km/h. Hỏi hai xe ô tô đó gặp nhau lúc mấy giờ? Biết quãng đường \(AB\) dài \(135\,\)km.

Câu 4. (0,75 điểm)

Một vật thể đặc bằng kim loại dạng hình trụ có bán kính đường tròn đáy và chiều cao đều bằng \(6\) cm. Người ta khoan xuyên qua hai mặt đáy của vật thể đó theo phương vuông góc với mặt đáy, phần bị khoan là một lỗ hình trụ có bán kính đường tròn đáy bằng \(2\) cm (Hình 1). Tính thể tích phần còn lại của vật thể đó.

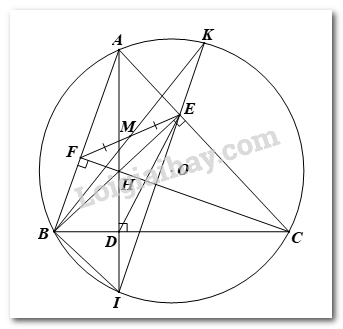
Câu 5. (3,0 điểm)

Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right)\). Các đường cao \(AD,\,\,BE\) và \(CF\) của tam giác \(ABC\) cắt nhau tại \(H.\)

a) Chứng minh \(BCEF\) và \(CDHE\) là các tứ giác nội tiếp.

b) Chứng minh \(EB\) là tia phân giác của \(\angle FED\) và tam giác \(BFE\) đồng dạng với tam giác \(DHE.\)

c) Giao điểm của \(AD\) với đường tròn \(\left( O \right)\) là \(I\) (\(I\) khác \(A\)), \(IE\) cắt đường tròn \(\left( O \right)\) tại \(K\) (\(K\) khác \(I\)). Gọi \(M\) là trung điểm của đoạn thẳng \(EF.\) Chứng minh rằng ba điểm \(B,\,\,M,\,\,K\) thẳng hàng.

Câu 6. (0,75 điểm)

Cho ba số thực dương \(x,\,\,y,\,\,z\) thỏa mãn điều kiện \({x^2} \ge {y^2} + {z^2}.\) Tìm giá trị nhỏ nhất của biểu thức: \(P = \dfrac{1}{{{x^2}}}\left( {{y^2} + {z^2}} \right) + {x^2}\left( {\dfrac{1}{{{y^2}}} + \dfrac{1}{{{z^2}}}} \right) + 2016.\)

Lời giải chi tiết

Câu 1. (1,5 điểm)

Cho hai biểu thức: \(A = \sqrt {50}  - 3\sqrt 8  + \sqrt {{{\left( {\sqrt 2  + 1} \right)}^2}} ;\)\(B = \dfrac{{x\sqrt x  - \sqrt x }}{{x - 1}} + \dfrac{{x - 1}}{{\sqrt x  + 1}}\) (với \(x \ge 0,\,\,x \ne 1\)).

a) Rút gọn các biểu thức \(A,\,\,B.\)

b) Tìm các giá trị của \(x\) sao cho \(A \le B.\)

Phương pháp:

a) + Sử dụng hằng đẳng thức: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)

Thực hiện các phép tính với căn bậc hai.

+ Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a  - \sqrt b } \right)\left( {\sqrt a  + \sqrt b } \right)\) xác định mẫu thức chung của biểu thức

Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.

b) Giải bất phương trình: \(A \le B.\)

Cách giải:

a) \(A = \sqrt {50}  - 3\sqrt 8  + \sqrt {{{\left( {\sqrt 2  + 1} \right)}^2}} \)

    \(\begin{array}{l}A = 5\sqrt 2  - 6\sqrt 2  + \left| {\sqrt 2  + 1} \right|\\A =  - \sqrt 2  + \sqrt 2  + 1\\A = 1\end{array}\)

\(B = \dfrac{{x\sqrt x  - \sqrt x }}{{x - 1}} + \dfrac{{x - 1}}{{\sqrt x  + 1}}\)

\(B = \dfrac{{\sqrt x \left( {x - 1} \right)}}{{x - 1}} + \dfrac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{\sqrt x  + 1}}\)

\(B = \sqrt x  + \sqrt x  - 1 = 2\sqrt x  - 1.\)

b) Để \(A \le B\)\( \Leftrightarrow 1 \le 2\sqrt x  - 1\)

                    \(\begin{array}{l} \Leftrightarrow 2\sqrt x  \ge 2\\ \Leftrightarrow \sqrt x  \ge 1\\ \Leftrightarrow x \ge 1\end{array}\)

Kết hợp với điều kiện \(x \ge 0,x \ne 1\) thì \(x > 1.\)

Câu 2. (1,5 điểm)

1) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + \dfrac{1}{{\sqrt y }} = 3\\x - \dfrac{1}{{\sqrt y }} = 0\end{array} \right. \cdot \)

2) Bạn Nam hiện có \(50\,000\) đồng. Để phục vụ cho việc học tập, bạn muốn mua một quyển sách tham khảo Toán có giá \(150\,000\) đồng. Vì thế, bạn Nam đã lên kế hoạch mỗi ngày tiết kiệm \(5\,000\) đồng. Gọi số tiền bạn Nam tiết kiệm được sau \(x\) (ngày) (gồm cả tiền hiện có và tiền tiết kiệm được hàng ngày) là \(y\) (đồng).

a) Lập công thức tính \(y\) theo \(x\).

b) Hỏi sau bao nhiêu ngày bạn Nam có vừa đủ tiền để mua được quyển sách tham khảo Toán?

Phương pháp:

1) Đặt điều kiện để hệ phương trình có nghĩa.

Biểu thức \(\dfrac{1}{{\sqrt {h\left( x \right)} }}\) xác định \( \Leftrightarrow h\left( x \right) > 0\)

Vận dụng phương pháp cộng đại số, tìm được \(x\) và \(y\), kết luận nghiệm của hệ phương trình

2) a) Vận dụng kiến thức của hàm số bậc nhất

b) Thay \(y = 150\,000\) vào công thức vừa lập được ở ý a, từ đó tìm được số ngày cần tiết kiệm tiền của Nam.

Cách giải:

1) ĐK: \(y > 0.\)

\(\left\{ \begin{array}{l}2x + \dfrac{1}{{\sqrt y }} = 3\\x - \dfrac{1}{{\sqrt y }} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 3\\x - \dfrac{1}{{\sqrt y }} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\\dfrac{1}{{\sqrt y }} = 1\end{array} \right. \cdot \)

Với \(\dfrac{1}{{\sqrt y }} = 1 \Rightarrow \sqrt y  = 1 \Leftrightarrow y = 1\,\,\)(thõa mãn \(y > 0\))

Vậy hệ phương trình có nghiệm duy nhất là \(\left( {x,y} \right) = \left( {1;1} \right).\)

2) a) Công thức tính \(y\) theo \(x\) là \(y = 5000x + 50\,000\) (đồng).

b) Bạn Nam có vừa đủ tiền mua được quyển sách tham khảo Toán đó khi

     \(5000x + 50\,000 = 150\,000\)

\(\begin{array}{l} \Leftrightarrow 5000x = 150000 - 50000\\ \Leftrightarrow 5000x = 100000\end{array}\)

\( \Leftrightarrow x = 20\) (ngày).

Vậy sau \(20\)ngày tiết kiệm, bạn Nam vừa đủ tiền mua quyển sách tham khảo Toán.

Câu 3. (2,5 điểm)

1) Cho phương trình \({x^2} - 2(m + 1)x + {m^2} + 2 = 0\)\(\left( 1 \right)\) (\(x\) là ẩn số, \(m\) là tham số).

a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1.\)

b) Xác định các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn điều kiện \(x_1^2 + 2\left( {m + 1} \right){x_2} = 12m + 2\).

2) Bài toán có nội dung thực tế:

 Lúc \(9\) giờ sáng, một xe ô tô khởi hành từ \(A\) đến \(B\) với vận tốc không đổi trên cả quãng đường là \(55\,\)km/h. Sau khi xe ô tô này đi được \(20\)phút thì cũng trên quãng đường đó, một xe ô tô khác bắt đầu đi từ \(B\) về \(A\) với vận tốc không đổi trên cả quãng đường là \(45\)km/h. Hỏi hai xe ô tô đó gặp nhau lúc mấy giờ? Biết quãng đường \(AB\) dài \(135\,\)km.

Phương pháp:

1) a) Thay \(m = 1\) vào phương trình \(\left( 1 \right)\)

Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a + b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = 1;{x_2} = \dfrac{c}{a}\)

b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta  > 0\) (hoặc \(\Delta ' > 0\))

Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(m\)

Thay \({x_1} + {x_2}\) theo \(m\) vào biểu thức \(x_1^2 + 2\left( {m - 1} \right){x_2} = 12m + 2\) ta được phương trình có \({x_1} + {x_2};{x_1}.{x_2}\)

Biến đổi, tìm \(m\)

2) Gọi thời gian xe ô tô đi từ \(A\) đến điểm gặp nhau của hai xe ô tô là \(x\) (giờ), (điều kiện \(x > \dfrac{1}{3}\)). (Với \(20\) phút bằng \(\dfrac{1}{3}\) giờ).

Tính được thời gian ô tô đi từ \(B\) đến điểm hai xe gặp nhau; Tính được quãng đường đi từ \(A\) về \(B\) và ngược lại

Từ đó lập được phương trình, giải phương trình, đối chiếu điều kiện và kết luận.

Cách giải:

1) a) Với \(m = 1\) phương trình \(\left( 1 \right)\) có dạng \({x^2} - 4x + 3 = 0.\)

Vì \(a + b + c = 1 + ( - 4) + 3 = 0\) nên phương trình có hai nghiệm là \({x_1} = 1;\,\,{x_2} = 3.\)

Vậy phương trình có hai nghiệm \({x_1} = 1;\,\,{x_2} = 3\) khi \(m = 1.\)

b) Có \(\Delta ' = {\left[ { - (m + 1)} \right]^2} - \left( {{m^2} + 2} \right) = {m^2} + 2m + 1 - {m^2} - 2 = 2m - 1.\)

Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) khi \(\Delta ' > 0\) \( \Leftrightarrow 2m - 1 > 0 \Leftrightarrow m > \dfrac{1}{2}.\)

Khi đó theo hệ thức Vi-ét \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2(m + 1)\\{x_1}{x_2} = {m^2} + 2\end{array} \right.\left( * \right).\)           

Thay \(2\left( {m + 1} \right) = {x_1} + {x_2}\) vào biểu thức \(x_1^2 + 2\left( {m + 1} \right){x_2} = 12m + 2\) được

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,x_1^2 + \left( {{x_1} + {x_2}} \right){x_2} = 12m + 2\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - {x_1}{x_2} = 12m + 2\,\,\left( 2 \right).\end{array}\)

Thay \(\left( * \right)\) vào phương trình \(\left( 2 \right)\) ta được:

\(\begin{array}{l}\,\,\,\,\,\,\,\,4{\left( {m + 1} \right)^2} - \left( {{m^2} + 2} \right) = 12m + 2\\ \Leftrightarrow 3{m^2} - 4m = 0\\ \Leftrightarrow m\left( {3m - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\3m - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\left( {ktm\,\,do\,\,m > \dfrac{1}{2}} \right)\\m = \dfrac{4}{3}\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy với \(m = \dfrac{4}{3}\) phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 + 2\left( {m + 1} \right){x_2} = 12m + 2.\)

Cách giải:

2) Gọi thời gian xe ô tô đi từ \(A\) đến điểm gặp nhau của hai xe ô tô là \(x\) (giờ), (điều kiện \(x > \dfrac{1}{3}\)). (Với \(20\) phút bằng \(\dfrac{1}{3}\) giờ).

Khi đó, thời gian ô tô đi từ \(B\) đến điểm hai xe gặp nhau là \(x - \dfrac{1}{3}\) (giờ).

Vì xe ô tô đi từ \(A\) đến \(B\) đi với vận tốc là \(55\) km/h nên quãng đường xe đó đi đến điểm hai xe gặp nhau là \(55x\) (km).

Vì xe ô tô đi từ \(B\) về \(A\) với vận tốc là \(45\) km/h nên quãng đường xe đó đi đến điểm hai xe gặp nhau là \(45\,\left( {x - \dfrac{1}{3}} \right)\,\)(km).

Do hai xe chuyển động ngược chiều và đi trên quãng đường dài \(135\,\)km nên có phương trình:

\(\begin{array}{l}\,\,\,\,\,\,\,55x + 45\left( {x - \dfrac{1}{3}} \right) = 135\\ \Leftrightarrow 100x - 15 = 135\\ \Leftrightarrow 100x = 150\\ \Leftrightarrow x = \dfrac{3}{2}\left( {tm\,\,do\,\,x > \dfrac{1}{3}} \right)\end{array}\)

Vậy hai xe gặp nhau lúc \(10h30'\)

Câu 4. (0,75 điểm)

Một vật thể đặc bằng kim loại dạng hình trụ có bán kính đường tròn đáy và chiều cao đều bằng \(6\) cm. Người ta khoan xuyên qua hai mặt đáy của vật thể đó theo phương vuông góc với mặt đáy, phần bị khoan là một lỗ hình trụ có bán kính đường tròn đáy bằng \(2\) cm (Hình 1). Tính thể tích phần còn lại của vật thể đó.

Phương pháp:

Thể tích của hình trụ có bán kính đáy là \(R\), chiều cao \(h\) được tính theo công thức \(V = \pi {r^2}h\)

Cách giải:

Gọi thể tích của vật thể hình trụ \({V_1}\) thì \({V_1} = \pi R_1^2h = {6^2}.6\pi  = 216\pi \,(c{m^3}).\)

Gọi thể tích của lỗ khoét hình trụ đó là \({V_2}\) thì \({V_2} = \pi R_2^2h = {2^2}.6\pi  = 24\pi \,(c{m^3}).\)

Gọi thể tích phần còn lại của vật thể đó là \(V\)thì \(V = {V_1} - {V_2} = 216\pi  - 24\pi  = 192\pi \,(c{m^3}).\)

Câu 5. (3,0 điểm)

Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right)\). Các đường cao \(AD,\,\,BE\) và \(CF\) của tam giác \(ABC\) cắt nhau tại \(H.\)

a) Chứng minh \(BCEF\) và \(CDHE\) là các tứ giác nội tiếp.

b) Chứng minh \(EB\) là tia phân giác của \(\angle FED\) và tam giác \(BFE\) đồng dạng với tam giác \(DHE.\)

c) Giao điểm của \(AD\) với đường tròn \(\left( O \right)\) là \(I\) (\(I\) khác \(A\)), \(IE\) cắt đường tròn \(\left( O \right)\) tại \(K\) (\(K\) khác \(I\)). Gọi \(M\) là trung điểm của đoạn thẳng \(EF.\) Chứng minh rằng ba điểm \(B,\,\,M,\,\,K\) thẳng hàng.

Phương pháp:

a) Vận dụng dấu hiệu nhận biết:

+ Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.

+ Tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau là tứ giác nội tiếp.

b) \(\left\{ \begin{array}{l}\angle BEF = \angle BED\\\angle EBF = \angle HDE\end{array} \right. \Rightarrow \Delta BFE \sim \Delta DHE\left( {g.g} \right)\)

c) Ta sẽ chứng minh: \(\angle ABM = \angle ABK\), mà \(BM,BK\)nằm trên cùng nửa mặt phẳng bờ chứa \(AB\). Do đó hai tia \(BM\) và \(BK\) là hai tia trùng nhau hay \(B,M\)và \(K\) là ba điểm thẳng hàng.

Cách giải:

a) + Có \(BE,\,\,CF\)là các đường cao của tam giác \(ABC\) nên  \(\angle BFC = {90^0};\angle BEC = {90^0}\)

Tứ giác \(BCEF\)có: \(\angle BFC = \angle BEC = {90^0}\)

Mà hai đỉnh \(E,F\) kề nhau

\( \Rightarrow BCEF\) là tứ giác nội tiếp.

+ Có \(AD,\,BE\) là các đường cao của tam giác \(ABC\) nên  \(\angle HDC = {90^0},\angle HEC = {90^0}\)

Tứ giác \(CDHE\)có: \(\angle HDC + \angle HEC = {180^0}\) mà \(\angle HDC\) và \(\angle HEC\) là hai  góc đối nhau nên \(CDHE\) là tứ giác nội tiếp.

b) Do \(BCEF\) là tứ giác nội tiếp nên \(\angle BEF = \angle BCF\)(góc nội tiếp cùng chắn \(cungBF\)) hay \(\angle BEF = \angle HCD\,\,\,\left( 1 \right)\)

Do \(CDHE\) là tứ giác nội tiếp nên \(\angle HED = \angle HCD\) (góc nội tiếp cùng chắn \(cungHD\)) \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\angle BEF = \angle HED\) hay \(\angle BEF = \angle BED\).

Do đó \(EB\) là tia phân giác của \(\angle FED\).

Do \(BCEF\) là tứ giác nội tiếp nên \(\angle EBF = \angle ECF\)(góc nội tiếp cùng chắn \(cungEF\)) hay \(\angle EBF = \angle HCE\,\,\,\left( 3 \right)\).

Do \(CDHE\) là tứ giác nội tiếp nên \(\angle HDE = \angle HCE\) (góc nội tiếp cùng chắn \(cungHE\))\(\left( 4 \right)\).

Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) suy ra \(\angle EBF = \angle HDE\)

Xét \(\Delta BFE\)và \(\Delta DHE\) có \(\angle BEF = \angle BED\) và \(\angle EBF = \angle HDE\) nên \(\Delta BFE \sim \Delta DHE\left( {g.g} \right)\)

c) Ta có \(\angle EBC = \angle CAD\) (cùng phụ với \(\angle ACB\)) hay \(\angle EBC = \angle CAI\)

Xét đường tròn \(\left( O \right)\) có \(\angle CAI = \angle CBI\) (góc nội tiếp cùng chắn \(cungCI\))

Nên \(\angle EBC = \angle CBI\) hay \(BC\) là phân giác của \(\angle HBI\), mà \(BC \bot HI\) suy ra \(\Delta HBI\) cân tại \(B\).

Do đó \(BC\) là đường trung trực của \(\Delta HBI\) suy ra \(D\) là trung điểm của \(HI.\)

Vì \(\Delta BFE \sim \Delta DHE \Rightarrow \dfrac{{BF}}{{DH}} = \dfrac{{FE}}{{HE}} \Rightarrow \dfrac{{BF}}{{2DH}} = \dfrac{{FE}}{{2HE}}\)

mà \(HI = 2DH\) (\(D\) là trung điểm của \(HI\)) và \(FM = \dfrac{{FE}}{2}\) (\(M\) là trung điểm của \(EF\))

Do đó \(\dfrac{{BF}}{{HI}} = \dfrac{{FM}}{{HE}} \cdot \)

Xét \(\Delta BFM\)và \(\Delta IHE\) có \(\dfrac{{BF}}{{HI}} = \dfrac{{FM}}{{HE}}\) và \(\angle BFM = \angle IHE\) nên \(\Delta BFM \sim \Delta IHE\left( {c.g.c} \right)\)

suy ra \(\angle FBM = \angle HIE\) (hai góc tương ứng) hay \(\angle ABM = \angle AIK\)\(\left( 5 \right).\)

Xét đường tròn \(\left( O \right)\) có \(\angle ABK = \angle AIK\) (góc nội tiếp cùng chắn \(cungAK\)) \(\left( 6 \right).\)

Từ \(\left( 5 \right)\) và \(\left( 6 \right)\) suy ra \(\angle ABM = \angle ABK\), mà \(BM,BK\)nằm trên cùng nửa mặt phẳng bờ chứa \(AB\). Do đó hai tia \(BM\) và \(BK\) là hai tia trùng nhau hay \(B,M\)và \(K\) là ba điểm thẳng hàng.

Câu 6. (0,75 điểm)

Cho ba số thực dương \(x,\,\,y,\,\,z\) thỏa mãn điều kiện \({x^2} \ge {y^2} + {z^2}.\) Tìm giá trị nhỏ nhất của biểu thức: \(P = \dfrac{1}{{{x^2}}}\left( {{y^2} + {z^2}} \right) + {x^2}\left( {\dfrac{1}{{{y^2}}} + \dfrac{1}{{{z^2}}}} \right) + 2016.\)

Phương pháp:

+ Áp dụng BĐT \(\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\)

+ Áp dụng BĐT \(AM - GM\) và \({x^2} \ge {y^2} + {z^2}\) (giả thiết của đề bài)

Cách giải:

Áp dụng BĐT \(\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\) ta được \(P \ge \dfrac{{{y^2} + {z^2}}}{{{x^2}}} + \dfrac{{4{x^2}}}{{{y^2} + {z^2}}} + 2016.\)

\(P \ge \dfrac{{{y^2} + {z^2}}}{{{x^2}}} + \dfrac{{{x^2}}}{{{y^2} + {z^2}}} + \dfrac{{3{x^2}}}{{{y^2} + {z^2}}} + 2016.\)

Áp dụng BĐT \(AM - GM\) và \({x^2} \ge {y^2} + {z^2}\) ta được

\(P \ge 2\sqrt {\dfrac{{{y^2} + {z^2}}}{{{x^2}}} \cdot \dfrac{{{x^2}}}{{{y^2} + {z^2}}}}  + \dfrac{{3\left( {{y^2} + {z^2}} \right)}}{{{y^2} + {z^2}}} + 2016 = 2021.\)

Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}{y^2} = {z^2}\\{x^2} = {y^2} + {z^2}\\\dfrac{{{y^2} + {z^2}}}{{{x^2}}} = \dfrac{{{x^2}}}{{{y^2} + {z^2}}}\end{array} \right. \Leftrightarrow y = z = \dfrac{x}{{\sqrt 2 }}.\)\(\)

Vậy giá trị nhỏ nhất của biểu thức \(P\) là \(2021\) đạt được khi \(y = z = \dfrac{x}{{\sqrt 2 }}.\)