Đề thi vào 10 môn Toán Đà Nẵng năm 2023Tải vềCâu 1: a) Tính (A = sqrt 4 {rm{ ;}} + sqrt {20} {rm{ ;}} - sqrt 5 {rm{ ;}} - 2) b) Cho biểu thức (B = left( {frac{1}{{sqrt x {rm{ ;}} + 1}} - frac{1}{{x + sqrt x }}} right):frac{{sqrt x {rm{ ;}} - 1}}{{{{left( {sqrt x {rm{ ;}} + 1} right)}^2}}}) với (x > 0,{mkern 1mu} x ne 1). Rút gọn biểu thức B và so sánh giá trị của B với 1. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
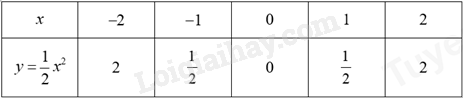
Đề bài Câu 1: a) Tính \(A = \sqrt 4 {\rm{ \;}} + \sqrt {20} {\rm{ \;}} - \sqrt 5 {\rm{ \;}} - 2\) b) Cho biểu thức \(B = \left( {\frac{1}{{\sqrt x {\rm{ \;}} + 1}} - \frac{1}{{x + \sqrt x }}} \right):\frac{{\sqrt x {\rm{ \;}} - 1}}{{{{\left( {\sqrt x {\rm{ \;}} + 1} \right)}^2}}}\) với \(x > 0,{\mkern 1mu} x \ne 1\). Rút gọn biểu thức B và so sánh giá trị của B với 1. Câu 2: Cho hàm số \(y = \frac{1}{2}{x^2}\) có đồ thị (P). a) Vẽ đồ thị (P). b) Đường thẳng \(y = {\rm{ \;}} - x + b\) (với b > 0) lần lượt cắt Ox, Oy tại E, F. Chứng minh rằng tam giác OEF vuông cân và tìm b để tâm đường tròn ngoại tiếp tam giác OEF là một điểm thuộc (P), với O là gốc tọa độ. Câu 3: a) Tổng của hai số bằng 23. Hai lần số này hơn số kia 1 đơn vị. Tìm hai số đó. b) Hai đội công nhân cùng dọn vệ sinh khu vực khán đài Lễ hội Pháo hoa quốc tế Đà Nẵng trong 1 giờ 12 phút thì xong. Nếu đội A làm 40 phút và đội B làm 2 giờ thì xong việc. Hỏi nếu làm riêng thì mỗi đội hoàn thành công việc trong bao lâu? Câu 4: Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 2m + 5 = 0{\mkern 1mu} {\mkern 1mu} \left( * \right)\), với m là tham số. a) Giải phương trình (*) khi m = 1. b) Tìm tất cả các giá trị của tham số m để phương trình (*) có hai nghiệm phân biệt \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) thoả mãn \(\sqrt {4x_1^2 + 4m{x_1} + {m^2}} {\rm{ \;}} + \sqrt {x_2^2 + 4m{x_2} + 4{m^2}} {\rm{ \;}} = 7m + 2\). Câu 5: Cho đường tròn (O) có hai đường kính AC, BD (A khác B, D). Trên đoạn BC lấy điểm E (E khác B, C), đường thẳng ED cắt đường tròn (O) tại điểm thứ hai là F. a) Chứng minh rằng AB = CD và \(\angle CFD = \angle BCA\). b) Đường thẳng qua E vuông góc với BC cắt tia AF tại G. Chứng minh rằng tứ giác CEFG nội tiếp và CD.EG = CB.CE. c) Gọi H là giao điểm của tia GE và AD. Đường thẳng qua H, song song với AC cắt đường thẳng qua E, song song với FC tại K. Chứng minh rằng ba điểm G, C, K thẳng hàng. ----- HẾT ----- Lời giải chi tiết Câu 1 (VD): Phương pháp: a) Căn bậc hai của một số \(a\) là một số \(x\) sao cho \({x^2} = a\) b) Quy đồng và rút gọn sử dụng hằng đẳng thức. Cách giải: a) Tính \(A = \sqrt 4 + \sqrt {20} - \sqrt 5 - 2\) Ta có: \(\begin{array}{l}A = \sqrt 4 + \sqrt {20} - \sqrt 5 - 2\\A = \sqrt {{2^2}} + \sqrt {{2^2}.5} - \sqrt 5 - 2\\A = 2 + 2\sqrt 5 - \sqrt 5 - 2\\A = \left( {2 - 2} \right) + \left( {2\sqrt 5 - \sqrt 5 } \right)\\A = \sqrt 5 \end{array}\) Vậy \(A = \sqrt 5 \). b, Cho biểu thức \(B = \left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{x + \sqrt x }}} \right):\frac{{\sqrt x - 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}}\) với \(x > 0,\,x \ne 1\). Rút gọn biểu thức B và so sánh giá trị của B với 1. Điều kiện xác định: \(x > 0,\,x \ne 1\). \(\begin{array}{l}B = \left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}}} \right):\frac{{\sqrt x - 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}}\\B = \left( {\frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x + 1} \right)}} - \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}}} \right):\frac{{\sqrt x - 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}}\\B = \frac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)}}.\frac{{{{\left( {\sqrt x + 1} \right)}^2}}}{{\sqrt x - 1}}\\B = \frac{{\sqrt x + 1}}{{\sqrt x }}\end{array}\) Ta có: \(B = \frac{{\sqrt x + 1}}{{\sqrt x }} = 1 + \frac{1}{{\sqrt x }} > 1\,\,;\forall x > 0,x \ne 1\). Vậy với \(x > 0,\,x \ne 1\) thì \(B = \frac{{\sqrt x + 1}}{{\sqrt x }} > 1.\) Câu 2 (VD): Cách giải: a) Vẽ đồ thị (P). Ta có bảng giá trị sau:
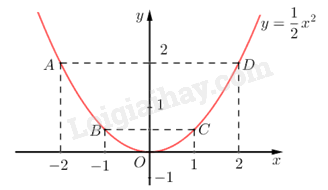
\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2;2} \right);B\left( { - 1;\frac{1}{2}} \right);\,\,C\left( {1;\frac{1}{2}} \right);\,\,D\left( {2;2} \right)\) Hệ số \(a = \frac{1}{2} > 0\)nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng. Ta vẽ được đồ thị hàm số \(y = \frac{1}{2}{x^2}\) như sau:
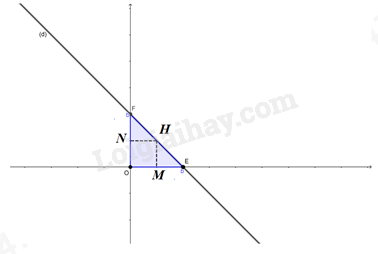
b) Đường thẳng \(y = - x + b\) (với b > 0) lần lượt cắt Ox, Oy tại E, F. Chứng minh rằng tam giác OEF vuông cân và tìm b để tâm đường tròn ngoại tiếp tam giác OEF là một điểm thuộc (P), với O là gốc tọa độ. Cho \(y = 0 \Rightarrow - x + b = 0 \Leftrightarrow x = b\) => Đường thẳng \(y = - x + b\) cắt Ox tại E(b;0). Cho \(x = 0 \Rightarrow y = 0 + b = b\) => Đường thẳng \(y = - x + b\) cắt Oy tại F(0;b).
Xét \(\Delta OEF\) có: \(\left\{ \begin{array}{l}OE \bot OF\,\,\left( {do\,\,Ox \bot Oy} \right)\\OE = OF = b\,\,\left( {do\,\,b > 0} \right)\end{array} \right.\) \( \Rightarrow \Delta OEF\) vuông cân tại O. => Tâm đường tròn ngoại tiếp \(\Delta OEF\) là trung điểm cạnh huyền EF. Gọi tâm đường tròn ngoại tiếp \(\Delta OEF\)là H. Gọi M, N lần lượt là hình chiếu của H lên Ox, Oy. Ta có \(\left\{ \begin{array}{l}HM \bot Ox\\OF \bot Ox\end{array} \right. \Rightarrow HM//OF\) (từ vuông góc đến song song). Mà H là trung điểm của EF => M là trung điểm của OE (Tính chất đường trung bình của tam giác). \( \Rightarrow HM\) là đường trung bình của tam giác OEF \( \Rightarrow HM = \frac{1}{2}OF = \frac{b}{2}\). Chứng minh tương tự ta tính được \(HN = \frac{b}{2}\). \( \Rightarrow H\left( {\frac{b}{2};\frac{b}{2}} \right)\). Để tâm đường tròn ngoại tiếp tam giác OEF là một điểm thuộc (P) \( \Leftrightarrow H\left( {\frac{b}{2};\frac{b}{2}} \right) \in (P)\). \(\begin{array}{l} \Leftrightarrow \frac{b}{2} = \frac{1}{2}.{\left( {\frac{b}{2}} \right)^2}\\ \Leftrightarrow \frac{b}{2} = \frac{{{b^2}}}{8}\\ \Leftrightarrow {b^2} - 4b = 0\\ \Leftrightarrow b(b - 4) = 0\\ \Leftrightarrow \left[ \begin{array}{l}b = 0\,\,(L)\\b = 4\,\,(TM)\end{array} \right.\end{array}\) Vậy \(b = 4\)là giá trị cần tìm. Câu 3 (VD): Cách giải: a) Tổng của hai số bằng 23. Hai lần số này hơn số kia 1 đơn vị. Tìm hai số đó. Gọi số thứ nhất là a, số thứ hai là b. Theo đề bài: Tổng của hai số bằng 23, ta có phương trình: a + b = 23; Hai lần số này hơn số kia 1 đơn vị, ta có phương trình: 2a – b = 1. Theo bài ra ta có hệ phương trình: \(\left\{ \begin{array}{l}a + b = 23\\2a - b = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + b = 23\\3a = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + b = 23\\a = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 8\\b = 15\end{array} \right.\). Vậy số thứ nhất là 8, số thứ hai là 15. b) Hai đội công nhân cùng dọn vệ sinh khu vực khán đài Lễ hội Pháo hoa quốc tế Đà Nẵng trong 1 giờ 12 phút thì xong. Nếu đội A làm 40 phút và đội B làm 2 giờ thì xong việc. Hỏi nếu làm riêng thì mỗi đội hoàn thành công việc trong bao lâu? Đổi 1 giờ 12 phút = \(\frac{6}{5}\)h; 40 phút = \(\frac{2}{3}\)h Gọi thời gian đội A làm riêng hoàn thành công việc là x (h), (\(x > \frac{6}{5}\)) thời gian đội B làm riêng hoàn thành công việc là y (h); (\(y > \frac{6}{5}\)) Trong 1 giờ, đội A làm được \(\frac{1}{x}\) công việc; đội B làm được \(\frac{1}{y}\) công việc. => 1 giờ hai đội cùng làm được \(\frac{1}{x} + \frac{1}{y}\) (công việc) Theo đề bài, hai đội làm cùng nhau thì sau 1 giờ 12 phút = \(\frac{6}{5}\)h xong công việc nên ta có phương trình: \(\frac{6}{5}.\left( {\frac{1}{x} + \frac{1}{y}} \right) = 1 \Leftrightarrow \frac{1}{x} + \frac{1}{y} = \frac{5}{6}\) Theo đề bài, nếu đội A làm 40 phút = \(\frac{2}{3}\)h và đội B làm 2 giờ thì xong công việc nên ta có phương trình: \(\frac{2}{{3x}} + \frac{2}{y} = 1\) Ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{5}{6}\\\frac{2}{{3x}} + \frac{2}{y} = 1\end{array} \right.\). Đặt \(\left\{ \begin{array}{l}\frac{1}{x} = u\\\frac{1}{y} = v\end{array} \right.\), hệ phương trình trở thành: \(\left\{ \begin{array}{l}u + v = \frac{5}{6}\\\frac{2}{3}u + 2v = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = \frac{5}{6} - u\\\frac{2}{3}u + 2v = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = \frac{5}{6} - u\\\frac{2}{3}u + 2\left( {\frac{5}{6} - u} \right) = 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}v = \frac{5}{6} - u\\\frac{2}{3}u + \frac{5}{3} - 2u = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = \frac{5}{6} - u\\\frac{4}{3}u = \frac{2}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = \frac{5}{6} - u\\u = \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = \frac{1}{3}\\u = \frac{1}{2}\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}\frac{1}{x} = \frac{1}{2}\\\frac{1}{y} = \frac{1}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\) (thỏa mãn) Vậy thời gian đội A làm riêng hoàn thành công việc là 2 giờ; thời gian đội B làm riêng hoàn thành công việc là 3 giờ. Câu 4 (VD): Cách giải: a) Giải phương trình (*) khi m = 1. Thay m = 1 vào phương trình (*) ta được: \(\begin{array}{l}{x^2} - 2\left( {1 + 1} \right)x + 1 - 2 + 5 = 0 \Leftrightarrow {x^2} - 4x + 4 = 0\\ \Leftrightarrow {\left( {x - 2} \right)^2} = 0 \Leftrightarrow x - 2 = 0 \Leftrightarrow x = 2\end{array}\) Vậy khi m = 1 phương trình có nghiệm duy nhất x = 2. b) Tìm tất cả các giá trị của tham số m để phương trình (*) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thoả mãn \(\sqrt {4x_1^2 + 4m{x_1} + {m^2}} + \sqrt {x_2^2 + 4m{x_2} + 4{m^2}} = 7m + 2\). Ta có: \(\begin{array}{l}\Delta ' = {\left( {m + 1} \right)^2} - \left( {{m^2} - 2m + 5} \right)\\\,\,\,\,\,\, = {m^2} + 2m + 1 - {m^2} + 2m - 5\\\,\,\,\,\,\, = 4m - 4\end{array}\) Để phương trình (*) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \(\Delta ' > 0 \Leftrightarrow 4m - 4 > 0 \Leftrightarrow m > 1.\) Ta có: \(\begin{array}{l}\sqrt {4x_1^2 + 4m{x_1} + {m^2}} + \sqrt {x_2^2 + 4m{x_2} + 4{m^2}} = 7m + 2\\ \Leftrightarrow \sqrt {{{\left( {2{x_1} + m} \right)}^2}} + \sqrt {{{\left( {{x_2} + 2m} \right)}^2}} = 7m + 2\\ \Leftrightarrow \left| {2{x_1} + m} \right| + \left| {{x_2} + 2m} \right| = 7m + 2\end{array}\) Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2 > 0\,\,\left( {do\,\,m > 1} \right)\\{x_1}{x_2} = {m^2} - 2m + 5 = {\left( {m - 1} \right)^2} + 4 > 0\,\,\forall m\end{array} \right.\). \( \Rightarrow \left\{ \begin{array}{l}{x_1} > 0\\{x_2} > 0\end{array} \right.\,\,\forall m > 1 \Rightarrow \left\{ \begin{array}{l}2{x_1} + m > 0\\{x_2} + 2m > 0\end{array} \right.\,\,\forall m\). Khi đó ta có: \(\begin{array}{l}\left| {2{x_1} + m} \right| + \left| {{x_2} + 2m} \right| = 7m + 2\\ \Leftrightarrow 2{x_1} + m + {x_2} + 2m = 7m + 2\\ \Leftrightarrow 2{x_1} + {x_2} = 4m + 2\\ \Leftrightarrow 2m + 2 + {x_1} = 4m + 2\\ \Leftrightarrow {x_1} = 2m\\ \Rightarrow {x_2} = 2m + 2 - {x_1} = 2\end{array}\) \(\begin{array}{l} \Rightarrow {x_1}{x_2} = 4m = {m^2} - 2m + 5\\ \Leftrightarrow {m^2} - 6m + 5 = 0\end{array}\) Ta có \(a + b + c = 1 + \left( { - 6} \right) + 5 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{m_1} = 1\,\,\left( {Ktm} \right)\\{m_2} = 5\,\,\left( {tm} \right)\end{array} \right.\). Vậy m = 5. Câu 5 (VD): Cách giải:
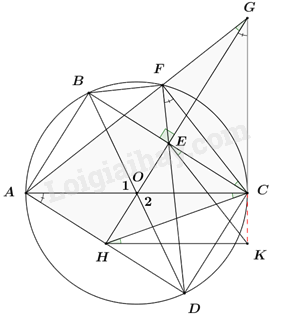
a) Chứng minh rằng AB = CD và \(\angle CFD = \angle BCA\). +) Chứng minh AB = CD Xét tam giác AOB và tam giác COD có: \(OA = OC\,\,\left( { = R} \right)\) \(\angle {O_1} = \angle {O_2}\) (đối đỉnh) \(\begin{array}{l}OB = OD\,\,\left( { = R} \right)\\ \Rightarrow \Delta AOB = \Delta COD\,\,\left( {c.g.c} \right)\end{array}\) \( \Rightarrow \) AB = CD (2 cạnh tương ứng) (đpcm) +) Chứng minh góc CFD = góc BCA Ta có: \(\angle CFD = \angle CBD\) (hai góc nội tiếp cùng góc chắn cung CD). Lại có: \(OB = OC = R \Rightarrow \Delta OBC\) cân tại O \( \Rightarrow \angle OBC = \angle OCB\) (tính chất tam giác cân) \( \Rightarrow \angle CBD = \angle BCA\). Vậy \(\angle CFD = \angle BCA\,\,\left( {dpcm} \right)\). b) Đường thẳng qua E vuông góc với BC cắt tia AF tại G. Chứng minh rằng tứ giác CEFG nội tiếp và CD.EG = CB.CE. +) Chứng minh tứ giác CEFG nội tiếp Ta có: \(\angle AFC = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle CFG = {90^0}\). Xét tứ giác CEFG có: \(\angle CFG = \angle CEG = {90^0}\) . Mà hai đỉnh E, F kề nhau cùng nhìn dưới CG dưới hai góc bằng nhau => Tứ giác EFGC nội tiếp (dhnb) (đpcm) +) Chứng minh CD.EG = CB.CE Ta có: \(\angle EGC = \angle EFC\) (vì EFGC nội tiếp nên hai góc cùng chắn cung CE) Mà \(\angle DFC = \angle DBC\) (hai góc cùng chắn cung CD) hay \(\angle EFC = \angle DBC\) Do đó \(\angle EGC = \angle DBC\) Xét tam giác BCD và tam giác GEC có: \(\angle BCD = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle BCD = \angle GEC = {90^0}\). \(\angle DBC = \angle EGC\) (cmt). $\Rightarrow \Delta BCD\backsim \Delta GEC\,\,\left( g.g \right)$ \( \Rightarrow \frac{{CB}}{{CD}} = \frac{{EG}}{{CE}} \Rightarrow CD.EG = CB.CE\,\,(dpcm)\) c) Gọi H là giao điểm của tia GE và AD. Đường thẳng qua H, song song với AC cắt đường thẳng qua E, song song với FC tại K. Chứng minh rằng ba điểm G, C, K thẳng hàng. Vì CEFG là tứ giác nội tiếp (cmt) \( \Rightarrow \angle EGC = \angle EFC = \angle DFC\) (hai góc nội tiếp cùng chắn cung EC). Mà \(\angle DFC = \angle DAC\) (hai góc nội tiếp cùng chắn cung CD) \( \Rightarrow \angle EGC = \angle DAC\) \( \Rightarrow \angle HGC = \angle HAC\). Mà hai đỉnh A, G kề nhau cùng nhìn HC dưới hai góc bằng nhau. \( \Rightarrow AGCH\) là tứ giác nội tiếp (dhnb). \( \Rightarrow \angle AGH = \angle ACH = \angle FGE\) (hai góc nội tiếp cùng chắn cung AH). Mà CEFG là tứ giác nội tiếp (cmt) \( \Rightarrow \angle FGE = \angle FCE\) (hai góc nội tiếp cùng chắn cung EF). \( \Rightarrow \angle ACH = \angle FCE\). Ta có: EK // FC (gt) \( \Rightarrow \angle FCE = \angle CEK\) (so le trong) HK // AC (gt) \( \Rightarrow \angle ACH = \angle CHK\) (so le trong) \( \Rightarrow \angle CEK = \angle CHK\). Mà hai đỉnh E, H kề nhau cùng nhìn CK dưới hai góc bằng nhau \( \Rightarrow CEHK\) là tứ giác nội tiếp (dhnb). \( \Rightarrow \angle HEC + \angle HKC = {180^0}\). Mà \(\angle HEC = {90^0}\) (do \(GH \bot BC\) tại E) \( \Rightarrow \angle HKC = {90^0} \Rightarrow CK \bot HK\). Mà HK // AC (gt) \( \Rightarrow CK \bot AC\) (từ vuông góc đến song song). Mà \(CG \bot AC\,\,\left( {cmt} \right)\). Vậy G, C, K thẳng hàng.
|




















Danh sách bình luận