Đề thi vào 10 môn Toán Lào Cai năm 2021Tải vềCâu 1 (1,0 điểm): Tính giá trị các biểu thức sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
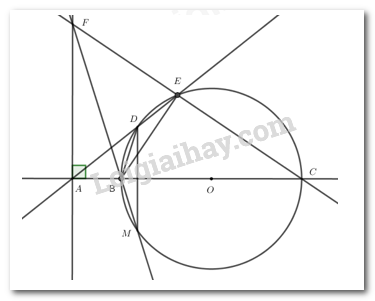
Đề bài Câu 1 (1,0 điểm): Tính giá trị các biểu thức sau: a) \(A = \sqrt {49} - 3\) b) \(B = \sqrt {{{\left( {10 - \sqrt 5 } \right)}^2}} + \sqrt 5 \) Câu 2 (1,5 điểm): Cho biểu thức \(P = \left( {\dfrac{{\sqrt x }}{{\sqrt x + 2}} + \dfrac{2}{{\sqrt x - 2}}} \right):\dfrac{{x + 4}}{{\sqrt x + 2}}\) (Với \(x \ge 0,\,x \ne 4\)). a) Rút gọn biểu thức P. b) Tính giá trị của \(x\) để \(P = \dfrac{1}{6}\). Câu 3 (1,0 điểm): a) Cho hàm số \(y = 2x + b\). Tìm \(b\) biết rằng đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 3. b) Cho parabol \(\left( P \right):\,\,y = {x^2}\) và đường thẳng \(d:\,\,y = \left( {m - 1} \right)x + m + 4\) (\(m\) là tham số). Tìm điều kiện của tham số \(m\) để \(d\) cắt \(\left( P \right)\) tại hai điểm nằm về hai phía của trục tung. Câu 4 (1,5 điểm): a) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{2x - y = 1}\\{x + y = 2}\end{array}} \right.\) b) Hai bạn An và Bình cùng may khẩu trang để ủng hộ địa phương đang có dịch bệnh Covid-19, thì mất hai ngày mới hoàn thành công việc. Nếu chỉ có một mình bạn An làm việc trong 4 ngày rồi nghỉ và bạn Bình làm tiếp trong 1 ngày nữa thì hoàn thành công việc. Hỏi mỗi người làm riêng một mình thì sau bao lâu sẽ hoàn thành công việc ? Câu 5 (2,0 điểm): a) Giải phương trình: \({x^2} + 5x - 6 = 0\) b) Tìm các giá trị của tham số \(m\) để phương trình \({x^2} - mx + m - 2 = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn: \({x_1} - {x_2} = 2\sqrt 5 \). Câu 6 (1,0 điểm): Cho tam giác \(ABC\) vuông tại \(A\), có độ dài các cạnh của tam giác thỏa mãn hệ thức \(B{C^2} = \left( {\sqrt 3 + 1} \right)A{C^2} + \left( {\sqrt 3 - 1} \right)AB.AC\), hãy tính số đo góc \(\angle ABC\). Câu 7 (2,0 điểm): Cho đường tròn \(\left( O \right)\), từ điểm \(A\) nằm ngoài đường tròn kẻ đường thẳng \(AO\) cắt đường tròn \(\left( O \right)\) tại \(B,C\) \(\left( {AB < AC} \right)\). Qua \(A\) kẻ đường thẳng không đi qua tâm \(O\) cắt đường tròn \(\left( O \right)\) tại \(D,E\) \(\left( {AD < AE} \right)\). Đường thẳng vuông góc với \(AB\) tại \(A\) cắt đường thẳng \(CE\) tại \(F\). a) Chứng minh tứ giác \(ABEF\) nội tiếp. b) Gọi \(M\) là giao điểm thứ hai của \(FB\) với đường tròn \(\left( O \right)\). Chứng minh: \(DM\) vuông góc với \(AC\). c) Chứng minh \(CE.CF + AD.AE = A{C^2}\) Lời giải Câu 1 (VD): Phương pháp: Vận dụng quy tắc khai phương một số, sau đó rút gọn biểu thức Cách giải: a) Ta có: \(A = \sqrt {49} - 3 = 7 - 3 = 4\). b) Ta có: \(B = \sqrt {{{\left( {10 - \sqrt 5 } \right)}^2}} + \sqrt 5 = \left| {10 - \sqrt 5 } \right| + \sqrt 5 = 10 - \sqrt 5 + \sqrt 5 = 10\) Câu 2 (VD): Phương pháp: a) Xác định điều kiện của biểu thức, áp dung quy tắc cộng, nhân chia các phân thức đại số để rút gọn biểu thức b) Áp dụng quy tắc hai phân thức bằng nhau, tìm giá trị của \(x\), đối chiếu điều kiện và kết luận nghiệm của phương trình Cách giải: a) Với \(x \ge 0,\,x \ne 4\) ta có: \(\begin{array}{l}P = \left( {\dfrac{{\sqrt x }}{{\sqrt x + 2}} + \dfrac{2}{{\sqrt x - 2}}} \right):\dfrac{{x + 4}}{{\sqrt x + 2}}\\P = \left( {\dfrac{{\sqrt x \left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} + \dfrac{{2\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}} \right):\dfrac{{x + 4}}{{\sqrt x + 2}}\\P = \dfrac{{x - 2\sqrt x + 2\sqrt x + 4}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}.\dfrac{{\sqrt x + 2}}{{x + 4}}\\P = \dfrac{{x + 4}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}.\dfrac{{\sqrt x + 2}}{{x + 4}}\\P = \dfrac{1}{{\sqrt x - 2}}\end{array}\) Vậy với \(x \ge 0,\,x \ne 4\) thì \(P = \dfrac{1}{{\sqrt x - 2}}\). b) Ta có: \(P = \dfrac{1}{6} \Leftrightarrow \dfrac{1}{{\sqrt x - 2}} = \dfrac{1}{6} \Leftrightarrow \sqrt x - 2 = 6 \Leftrightarrow \sqrt x = 8 \Leftrightarrow x = 64\,\,\left( {tm\,\,DKXD} \right)\). Vậy với \(x = 64\) thì \(P = \dfrac{1}{6}\). Câu 3 (VD): Phương pháp: a) Xác định tọa độ giao điểm của đồ thị và trục hoành tại điểm có hoàng độ là 3 là điểm: \(\left( {3;0} \right)\), sau đó thay vào hàm số để tìm giá tị của b. b) Xét phương trình hoành độ giao điểm của Parabol (P) và đường thẳng \(d\) , sau đó biện luận: \(\left( P \right)\) cắt \(d\) tại hai điểm nằm về hai phía của trục tung khi và chỉ khi phương trình (1) có hai nghiệm trái dấu, sử dụng hệ thức Vi – ét để tìm giá trị m. Cách giải: a) Vì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3 nên đồ thị hàm số đi qua điểm \(\left( {3;0} \right)\). Thay \(x = 3,y = 0\) vào hàm số ta được: \(2.3 + b = 0 \Leftrightarrow b = - 6\). Vậy \(b = - 6\). b) Hoành độ giao điểm của Parabol (P) và đường thẳng \(d\) là nghiệm của phương trình; \(\begin{array}{l}\,\,\,\,\,\,\,{x^2} = \left( {m - 1} \right)x + m + 4\\ \Leftrightarrow {x^2} - \left( {m - 1} \right)x - m - 4 = 0\,\,\,\,\left( 1 \right)\end{array}\) \(\left( P \right)\) cắt \(d\) tại hai điểm nằm về hai phía của trục tung khi và chỉ khi phương trình (1) có hai nghiệm trái dấu. \( \Leftrightarrow ac < 0 \Leftrightarrow - m - 4 < 0 \Leftrightarrow m > - 4\). Vậy \(m > - 4\) thì \(\left( P \right)\) cắt \(d\) tại hai điểm nằm về hai phía của trục tung. Câu 4 (VD): Phương pháp: a) Sử dụng phương pháp cộng đại số b) Vận dụng cách giải bài toán bằng cách lâp hệ phương trình: Gọi thời gian hoàn thành công việc một mình của An và Bình lần lượt là \(x,\,\,y\) (ngày; \(x,\,y > 0\)), sau đó xác định hai phương trình để tìm được \(x,\,\,y\), chú ý đối chiếu điều kiện. Cách giải: a) Ta có: \(\left\{ {\begin{array}{*{20}{c}}{2x - y = 1}\\{x + y = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3x = 3}\\{y = 2 - x}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2 - 1\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 1}\end{array}} \right.\). Vậy hệ phương trình đã cho có nghiệm \(\left( {x;y} \right) = \left( {1;\,\,1} \right)\). b) Gọi thời gian hoàn thành công việc một mình của An và Bình lần lượt là \(x,\,\,y\) (ngày; \(x,\,y > 0\)). Một ngày An hoàn thành được: \(\dfrac{1}{x}\) (công việc) Một ngày Bình hoàn thành được: \(\dfrac{1}{y}\) (công việc) Do hai bạn cùng là thì sau hai ngày xong công việc nên một ngày hai bạn hoành thành được: \(\dfrac{1}{2}\) (công việc) Ta có phương trình: \(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{2}\) (1) Bạn An làm 4 ngày được \(\dfrac{4}{x}\) (công việc) Vì một mình bạn An làm việc trong 4 ngày rồi nghỉ và bạn Bình làm tiếp trong 1 ngày nữa thì hoàn thành công việc nên ta có phương trình: \(\dfrac{4}{x} + \dfrac{1}{y} = 1\) (2) Từ (1) và (2) ta có hệ: \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{2}}\\{\dfrac{4}{x} + \dfrac{1}{y} = 1}\end{array}} \right.\) Đặt \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{1}{x} = a}\\{\dfrac{1}{y} = b}\end{array}} \right.\) thì hệ phương trình trở thành: \(\left\{ {\begin{array}{*{20}{c}}{a + b = \dfrac{1}{2}}\\{4a + b = 1}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}3a = \dfrac{1}{2}\\b = \dfrac{1}{2} - a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{6}\\b = \dfrac{1}{2} - \dfrac{1}{6}\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \dfrac{1}{6}}\\{b = \dfrac{1}{3}}\end{array}} \right.\) Thay vào cách đặt ta được \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{1}{x} = \dfrac{1}{6}}\\{\dfrac{1}{y} = \dfrac{1}{3}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 6\,\,\,\,\left( {tm} \right)}\\{y = 3\,\,\,\,\left( {tm} \right)}\end{array}} \right.\). Vậy An làm một mình sau 6 ngày xong công việc, Bình làm một mình sau 3 ngày xong công việc. Câu 5 (VD) Phương pháp: a) + Cách 1: Phân tích đa thức thành nhân tử, đưa phương trình về dạng phương trình tích: \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\) + Cách 2: Sử dụng công thức nghiệm của phương trình bậc hai môt ẩn. b) Tìm điều kiện để phương trình có hai nghiệm phân biệt, biến đổi biểu thức cần tính để xuất hiện \({x_1} + {x_2},{x_1}{x_2}\) sau đó vận dụng Hệ thức Vi – ét để tìm giá trị của \(m\). Chú ý: \({\left( {{x_1} - {x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2}\) Cách giải: a) Cách 1: \({x^2} + 5x - 6 = 0\) \(\begin{array}{l} \Leftrightarrow {x^2} - x + 6x - 6 = 0\\ \Leftrightarrow x\left( {x - 1} \right) + 6\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 6\end{array} \right.\end{array}\) Vậy tập nghiệm của phương trình là \(S = \left\{ { - 6;1} \right\}\). Cách 2: Ta có \(\Delta = {5^2} - 4.1.\left( { - 6} \right) = 49 > 0\) nên phương trình đã cho có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - 5 + \sqrt {49} }}{2} = 1\\{x_2} = \dfrac{{ - 5 - \sqrt {49} }}{2} = - 6\end{array} \right.\). Vậy tập nghiệm của phương trình là \(S = \left\{ { - 6;1} \right\}\). b) Phương trình \({x^2} - mx + m - 2 = 0\) có 2 nghiệm khi và chỉ khi \(\Delta > 0\). \(\begin{array}{l} \Leftrightarrow {\left( { - m} \right)^2} - 4\left( {m - 2} \right) > 0\\ \Leftrightarrow {m^2} - 4m + 8 > 0\end{array}\) \( \Leftrightarrow {\left( {m - 2} \right)^2} + 4 > 0\) (luôn đúng). Do đó phương trình đã cho luôn có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\). Theo hệ thức Vi –ét ta có:\(\left\{ \begin{array}{l}{x_2} + {x_2} = m\\{x_1}.{x_2} = m - 2\end{array} \right.\). Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,\,\,{x_1} - {x_2} = 2\sqrt 5 \\ \Rightarrow {\left( {{x_1} - {x_2}} \right)^2} = 20\\ \Leftrightarrow x_1^2 + x_2^2 - 2{x_2}{x_2} = 20\\ \Leftrightarrow \left( {x_1^2 + x_2^2 + 2{x_1}{x_2}} \right) - 4{x_1}{x_2} = 20\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 20\\ \Leftrightarrow {m^2} - 4\left( {m - 2} \right) = 20\\ \Leftrightarrow {m^2} - 4m - 12 = 0\,\,\left( 1 \right)\end{array}\) Ta có \({\Delta _m}' = {2^2} - 1.\left( { - 12} \right) = 16 > 0\) nên phương trình (1) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{m_1} = \dfrac{{2 + \sqrt {16} }}{1} = 6\\{m_2} = \dfrac{{2 - \sqrt {16} }}{1} = - 2\end{array} \right.\). Vậy \(m = 6\) hoặc \(m = - 2\) thỏa mãn yêu cầu bài toán. Câu 6 (VD) Phương pháp: Áp dụng định lý Py – ta – go để tìm độ dài các cạnh, vận dụng hệ thức lượng trong tam giác vuông để xác định \(\cot \angle ABC\). Cách giải: Áp dụng định lí Pytago ta có: \(B{C^2} = A{B^2} + A{C^2}\) \(\begin{array}{l} \Rightarrow A{B^2} + A{C^2} = \left( {\sqrt 3 + 1} \right)A{C^2} + \left( {\sqrt 3 - 1} \right)AB.AC\\ \Leftrightarrow A{B^2} = \sqrt 3 A{C^2} + \left( {\sqrt 3 - 1} \right)AB.AC\\ \Leftrightarrow A{B^2} - \left( {\sqrt 3 - 1} \right)AB.AC - \sqrt 3 A{C^2} = 0\\ \Leftrightarrow A{B^2} + AB.AC - \sqrt 3 AB.AC - \sqrt 3 A{C^2} = 0\\ \Leftrightarrow AB\left( {AB + AC} \right) - \sqrt 3 AC\left( {AB + AC} \right) = 0\\ \Leftrightarrow \left( {AB + AC} \right)\left( {AB - \sqrt 3 AC} \right) = 0\\ \Leftrightarrow AB = \sqrt 3 AC\,\,\left( {do\,\,AB + AC > 0} \right)\\ \Rightarrow \dfrac{{AB}}{{AC}} = \sqrt 3 \\ \Rightarrow \cot \angle ABC = \sqrt 3 \\ \Rightarrow \angle ABC = {30^0}\end{array}\) Vậy \(\angle ABC = {30^0}\). Câu 7 (VDC). Phương pháp: a) Vận dụng dấu hiệu nhận biết tứ giác nội tiếp: tứ giác có tổng hai góc đối ngau bằng \({180^0}\) là tứ giác nội tiếp. b) Chứng minh \(MD//AF\) và kết hợp với \(AF \bot AC\,\,\left( {gt} \right)\), suy ra \(MD \bot AC\) c) Chứng minh \(\Delta BEC\, \sim \Delta FAC\,\,\,\left( {g.g} \right)\), \(\Delta ABD \sim \Delta AEC\,\,\left( {g.g} \right)\) suy ra các hệ thức về tỉ lệ các cạnh, cộng vế với vế biến đổi để ra đẳng thức cần chứng minh Cách giải: a) Ta có \(BC\) là đường kính của \(\left( O \right)\) nên \(\angle BEC = {90^0}\) (góc nội tiếp chắn nửa đường tròn). \( \Rightarrow \angle BEF = 180^\circ - \angle BEC = 90^\circ \) (hai góc kề bù) Mà \(AB \bot AF \Rightarrow \angle BAF = 90^\circ \) Xét tứ giác \(ABEF\) ta có: \(\angle BEF + \angle BAF = {90^0} + {90^0} = {180^0}\). Vậy tứ giác \(ABEF\) nội tiếp (dhnb). b) Ta có \(\angle BED = \angle BMD = \dfrac{1}{2}sdcBD\) (2 góc nội tiếp cùng chắn cung \(BD\)). Mà \(\angle BED = \angle BEA = \angle BFA\) (hai góc nội tiếp cùng chắn cung \(B\) của tứ giác nội tiếp \(ABEF\)). \( \Rightarrow \angle BMD = \angle BFA\). Mà 2 góc này ở vị trí hai góc so le trong nên suy ra \(MD//AF\) (dhnb). Mà \(AF \bot AC\,\,\left( {gt} \right)\). Vậy \(MD \bot AC\) (đpcm). c) Xét \(\Delta BEC\) và \(\Delta FAC\) có: \(\angle BEC = \angle FAC = {90^0}\); \(\angle ACF\) chung \( \Rightarrow \)\(\Delta BEC\, \sim \Delta FAC\,\,\,\left( {g.g} \right)\) \( \Rightarrow \dfrac{{CE}}{{AC}} = \dfrac{{BC}}{{CF}} \Rightarrow CE.CF = AC.BC\) (1) Xét \(\Delta ABD\) và \(\Delta AEC\) có: \(\angle EAC\) chung; \(\angle ADB = \angle ACE\) (Góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp \(BDEC\)). \( \Rightarrow \Delta ABD \sim \Delta AEC\,\,\left( {g.g} \right)\) \( \Rightarrow \dfrac{{AD}}{{AC}} = \dfrac{{AB}}{{AE}} \Rightarrow AD.AE = AB.AC\) (2) Cộng vế theo vế của (1) với (2) ta được: \(CE.CF + AD.AE = AC.BC + AC.AB = AC.\left( {BC + AB} \right) = A{C^2}\). Vậy \(CE.CF + AD.AE = A{C^2}\) (đpcm).
|




















Danh sách bình luận