Đề thi vào 10 môn Toán Lào Cai năm 2019Tải vềCâu 1 (1,0 điểm): Tính giá trị các biểu thức sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
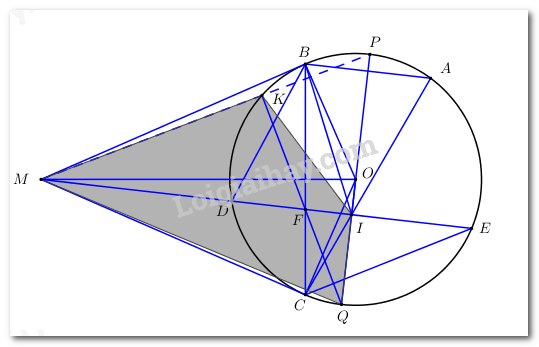
Đề bài Câu 1 (1,0 điểm): Tính giá trị các biểu thức sau: \(a)\,\sqrt 4 + 3\) \(b)\,\sqrt 5 + \sqrt {{{\left( {6 - \sqrt 5 } \right)}^2}} \) Câu 2 (1,5 điểm): Cho biểu thức \(H = \dfrac{{2{x^2} + 2x}}{{{x^2} - 1}} + \dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{\sqrt x - 1}}\) (với \(x \ge 0;\,x \ne 1\) ) a) Rút gọn biểu thức \(H.\) b) Tìm tất cả các giá trị của x để \(\sqrt x - H < 0\) Câu 3 (2,5 điểm): 1) Cho đường thẳng \(\left( d \right):y = x - 1\) và parabol \(\left( P \right):y = 3{x^2}\) a) Tìm tọa độ điểm \(A\) thuộc parabol \(\left( P \right)\) , biết điểm \(A\) có hoành độ \(x = - 1.\) b) Tìm \(b\) để đường thẳng \(\left( d \right)\) và đường thẳng \(\left( {d'} \right):y = \dfrac{1}{2}x + b\) cắt nhau tại một điểm trên trục hoành. 2) a) Giải hệ phương trình \(\left\{ \begin{array}{l}x + y = 5\\2x - y = 1\end{array} \right..\) b) Tìm tham số \(a\) để hệ phương trình \(\left\{ \begin{array}{l}x - y = a\\7x - 2y = 5a - 1\end{array} \right.\) có nghiệm duy nhất \(\left( {x;y} \right)\) thỏa mãn \(y = 2x.\) Câu 4 (2,0 điểm): a) Giải phương trình \({x^2} - 3x + 2 = 0\) b) Tìm các giá trị của tham số m để phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} = 0\) có hai nghiệm phân biệt \({x_1};\,{x_2}\) thỏa mãn: \({\left( {{x_1} - {x_2}} \right)^2} + 6m = {x_1} - 2{x_2}.\) Câu 5 (3,0 điểm): Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\). Kẻ hai tiếp tuyến \(MB;\,MC\)(B và C là các tiếp điểm) với đường tròn. Trên cung lớn BC lấy điểm A sao cho \(AB < AC\). Từ điểm M kẻ đường thẳng song song với AB, đường thẳng này cắt đường tròn \(\left( O \right)\) tại \(D\) và \(E\,\left( {MD < ME} \right)\) , cắt BC tại F, cắt AC tại I. a) Chứng minh tứ giác \(MBOC\) nội tiếp. b) Chứng minh \(FD.FE = FB.FC;\,\,FI.FM = FD.FE\) c) Đường thẳng \(OI\) cắt đường tròn \(\left( O \right)\) tại \(P\) và \(Q\) (P thuộc cung nhỏ AB). Đường thẳng \(QF\) cắt đường tròn \(\left( O \right)\) tại K (K khác Q). Chứng minh 3 điểm \(P,\,K,\,M\) thẳng hàng. Lời giải Câu 1 (TH) Phương pháp: Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Cách giải: a) \(\sqrt 4 + 3 = 2 + 3 = 5\). b) \(\sqrt 5 + \sqrt {{{\left( {6 - \sqrt 5 } \right)}^2}} = \sqrt 5 + \left| {6 - \sqrt 5 } \right| = \sqrt 5 + 6 - \sqrt 5 = 6\). Câu 2 (VD) Phương pháp: a) Quy đồng mẫu các phân thức rồi rút gọn biểu thức.’ b) Giải bất phương trình \(\sqrt x - H < 0\) để tìm \(x,\) đối chiếu với điều kiện rồi kết luận. Cách giải: a) Rút gọn biểu thức \(H.\) Với \(x \ge 0;x \ne 1\) ta có \(\begin{array}{l}H = \dfrac{{2{x^2} + 2x}}{{{x^2} - 1}} + \dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{\sqrt x - 1}} = \dfrac{{2x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{\sqrt x - 1}}\\\,\,\,\,\,\, = \dfrac{{2x}}{{x - 1}} + \dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{\sqrt x - 1}} = \dfrac{{2x}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{\sqrt x - 1}}\\\,\,\,\,\, = \dfrac{{2x + \sqrt x - 1 - \sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \dfrac{{2x - 2}}{{x - 1}}\\\,\,\,\, = \dfrac{{2\left( {x - 1} \right)}}{{x - 1}} = 2.\end{array}\) Vậy \(H = 2\) với \(x \ge 0;x \ne 1\). b) Tìm tất cả các giá trị của \(x\) để \(\sqrt x - H < 0.\) Điều kiện: \(x \ge 0;x \ne 1\) Theo đề bài ta có: \(\sqrt x - H < 0 \Leftrightarrow \sqrt x - 2 < 0 \Leftrightarrow \sqrt x < 2 \Leftrightarrow x < 4\) Kết hợp điều kiện \(x \ge 0;x \ne 1\) ta có \(0 \le x < 4;x \ne 1\) Vậy với \(0 \le x < 4;x \ne 1\) thì \(\sqrt x - H < 0.\) Câu 3 (VD) Phương pháp: 1) a) Thay hoành độ điểm \(x = - 1\) vào công thức hàm số của \(\left( P \right)\) để tìm tung độ điểm \(A.\) b) Gọi \(B\left( {{x_B};\,\,0} \right)\) là điểm thuộc trục hoành và là giao điểm của hai đường thẳng \(d,\,\,d'.\) Thay tọa độ điểm \(B\) vào phương trình đường thẳng \(d\) để tìm \({x_B}.\) Thay tọa độ điểm \(B\) vừa tìm được vào phương trình đường thẳng \(d'\) để tìm \(b.\) 2) a) Giải hệ phương trình bằng phương pháp thế. b) Hệ phương trình \(\left\{ \begin{array}{l}{a_1}x + {b_1}y = {c_1}\\{a_2}x + {b_2}y = {c_2}\end{array} \right.\) (với \({a_2}{b_2} \ne 0\)) có nghiệm duy nhất \( \Leftrightarrow \dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}.\) Tìm nghiệm duy nhất đó theo \(a\) rồi thế vào biểu thức bài cho để tìm \(a.\) Cách giải: 1) Cho đường thẳng \(\left( d \right):\,\,y = x - 1,\,\,\,\,\left( P \right):\,\,y = 3{x^2}.\) a) Điểm \(A\) có hoành độ là \(x = - 1\) và thuộc parabol \(\left( P \right):\,\,\,y = 3{x^2}\) nên thay hoành độ \(x = - 1\) vào hàm số ta được: \({y_A} = 3.{\left( { - 1} \right)^2} = 3.\) \( \Rightarrow A\left( { - 1;\,\,3} \right)\) thỏa mãn bài toán. b) Gọi \(B\left( {{x_B};\,\,0} \right)\) là điểm thuộc trục hoành và là giao điểm của hai đường thẳng \(d,\,\,d'.\) Ta có \(B\left( {{x_B};\,\,0} \right) \in \left( d \right):\,\,y = x - 1 \Rightarrow 0 = {x_B} - 1 \Leftrightarrow {x_B} = 1 \Rightarrow B\left( {1;\,\,0} \right).\) Lại có: \(B\left( {1;\,\,0} \right) \in \left( {d'} \right):\,\,y = \dfrac{1}{2}x + b \Rightarrow 0 = \dfrac{1}{2}.1 + b \Leftrightarrow b = - \dfrac{1}{2}.\) Vậy \(b = - \dfrac{1}{2}\) thỏa mãn bài toán. 2) a) Giải hệ phương trình:\(\left\{ \begin{array}{l}x + y = 5\\2x - y = 1\end{array} \right..\) \(\left\{ \begin{array}{l}x + y = 5\\2x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\y = 5 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5 - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right..\) Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\,\,y} \right) = \left( {2;\,\,3} \right).\) b) Tìm tham số \(a\) để hệ phương trình \(\left\{ \begin{array}{l}x - y = a\\7x - 2y = 5a - 1\end{array} \right.\) có nghiệm duy nhất \(\left( {x;\,\,y} \right)\) thỏa mãn \(y = 2x.\) Hệ phương trình có: \(\dfrac{1}{7} \ne \dfrac{{ - 1}}{{ - 2}} \Rightarrow \) Hệ phương trình \(\left\{ \begin{array}{l}x - y = a\,\,\,\,\,\left( 1 \right)\\7x - 2y = 5a - 1\,\,\,\,\left( 2 \right)\end{array} \right.\) có nghiệm duy nhất với mọi \(a.\) Theo đề bài ta có hệ phương trình có nghiệm duy nhất thỏa mãn \(y = 2x\) Thay \(y = 2x\) vào \(\left( 1 \right)\) ta được: \(x - 2x = a \Leftrightarrow - x = a \Leftrightarrow x = - a \Rightarrow y = - 2a.\) Thay \(x = - a;\,\,\,y = - 2a\) vào \(\left( 2 \right)\) ta được: \(\begin{array}{l}7\left( { - a} \right) - 2\left( { - 2a} \right) = 5a - 1\\ \Leftrightarrow - 7a + 4a = 5a - 1\\ \Leftrightarrow - 3a - 5a = - 1\\ \Leftrightarrow - 8a = - 1\\ \Leftrightarrow a = \dfrac{1}{8}.\end{array}\) Vậy \(a = \dfrac{1}{8}\) thỏa mãn bài toán. Câu 4 (VD) Phương pháp: a) Giải phương trình bậc hai bằng phương pháp nhẩm nghiệm. b) Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0.\) Áp dụng hệ thức Vi-et và hệ thức bài cho để tìm \(m\) sau đó đối chiếu với điều kiện rồi kết luận. Cách giải: a) Giải phương trình \({x^2} - 3x + 2 = 0\) Ta có: \(a = 1;b = - 3;c = 2 \Rightarrow a + b + c = 0\) . Khi đó phương trình có hai nghiệm phân biệt là: \({x_1} = 1;{x_2} = 2\) Vậy tập nghiệm của phương trình là: \(S = \left\{ {1;2} \right\}\) b) Tìm các giá trị của tham số m để phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} = 0\) (1) có hai nghiệm phân biệt \({x_1};\,{x_2}\) thỏa mãn \({\left( {{x_1} - {x_2}} \right)^2} + 6m = {x_1} - 2{x_2}\) Phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} = 0\) (1) có các hệ số: \(a = 1;b = - 2\left( {m - 1} \right);c = {m^2}\) \(\Delta ' = {\left[ { - \left( {m - 1} \right)} \right]^2} - {m^2} = {m^2} - 2m + 1 - {m^2} = 1 - 2m\) Phương trình có hai nghiệm phân biệt \({x_1};\,\,{x_2}\) khi và chỉ khi \(\Delta ' > 0 \Leftrightarrow 1 - 2m > 0 \Leftrightarrow m < \dfrac{1}{2}\) Áp dụng hệ thức Viet cho phương trình (1) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a} = 2\left( {m - 1} \right)\\{x_1}.{x_2} = \dfrac{c}{a} = {m^2}\end{array} \right.\) Theo đề bài ta có: \(\begin{array}{l}{\left( {{x_1} - {x_2}} \right)^2} + 6m = {x_1} - 2{x_2}\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} + 6m = {x_1} - 2{x_2}\\ \Leftrightarrow 4{\left( {m - 1} \right)^2} - 4{m^2} + 6m = {x_1} - 2{x_2}\\ \Leftrightarrow 4\left( {{m^2} - 2m + 1} \right) - 4{m^2} + 6m = {x_1} - 2{x_2}\\ \Leftrightarrow 4{m^2} - 8m + 4 - 4{m^2} + 6m = {x_1} - 2{x_2}\\ \Leftrightarrow - 2m + 4 = {x_1} - 2{x_2}\end{array}\) Khi đó kết hợp với \({x_1} + {x_2} = 2\left( {m - 1} \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right)\\{x_1} - 2{x_2} = - 2m + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} = 2m - 2\\{x_1} - 2{x_2} = - 2m + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3{x_2} = 4m - 6\\{x_1} + {x_2} = 2m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = \dfrac{4}{3}m - 2\\{x_1} = 2m - 2 - \dfrac{4}{3}m + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = \dfrac{4}{3}m - 2\\{x_1} = \dfrac{2}{3}m\end{array} \right.\) Thay \({x_1} = \dfrac{2}{3}m;{x_2} = \dfrac{4}{3}m - 2\) vào \({x_1}.{x_2} = {m^2}\) ta có: \(\begin{array}{l}\left( {\dfrac{4}{3}m - 2} \right).\dfrac{2}{3}m = {m^2} \Leftrightarrow \dfrac{{ - 1}}{9}{m^2} - \dfrac{4}{3}m = 0\\ \Leftrightarrow - m\left( {\dfrac{1}{9}m + \dfrac{4}{3}} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\,\,\,\,\left( {tm} \right)\\m = - 12\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy \(m = 0;m = - 12\) thỏa mãn yêu cầu bài toán. Câu 5 (VD): Phương pháp: a) Chứng minh tứ giác nội tiếp nhờ các dấu hiệu nhận biết. b) Chứng minh các tam giác đồng dạng từ đó suy ra các cặp cạnh tương ứng tỉ lệ và suy ra các đẳng thức cần chứng minh. c) Chứng minh \(\angle MKP = {180^0}\) rồi suy ra ba điểm \(M,\,\,K,\,\,P\) thẳng hàng. Cách giải:
a) Chứng minh tứ giác\(MBOC\) nội tiếp. Do \(MB,\,\,MC\) là 2 tiếp tuyến của đường tròn \(\left( O \right) \Rightarrow \angle OBM = \angle OCM = {90^0}\). Xét tứ giác \(MBOC\) có: \(\angle OBM + \angle OCM = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(MBOC\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800). b) Chứng minh \(FD.FE = FB.FC,\,\,FI.FM = FD.FE\). +) Xét tam giác \(FBD\) và tam giác \(FEC\) có: \(\angle BFD = \angle EFC\) (đối đỉnh); \(\angle FDB = \angle FCE\) (hai góc nội tiếp cùng chắn cung \(BE\)); . +) Ta có: \(AB//ME \Rightarrow \angle BAC = \angle DIC\) (đồng vị). Mà \(\angle BAC = \angle MBC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC). \( \Rightarrow \angle DIC = \angle MBC \Rightarrow \angle MBF = \angle CIF\,\,\left( * \right)\). Xét tam giác \(FBM\) và tam giác \(FIC\) có : \(\angle BFM = \angle IFC\) (đối đỉnh) ; \(\angle MBF = \angle CIF\,\,\left( {cmt} \right);\) (hai cạnh tương ứng). \( \Rightarrow FI.FM = FB.FC\,\,\,\left( 2 \right)\). Từ (1) và (2) \( \Rightarrow FI.FM = FD.FE\,\,\left( 3 \right)\). c) Đường thẳng \(OI\) cắt đường tròn \(\left( O \right)\) tại \(P\) và \(Q\) (\(P\) thuộc cung nhỏ \(AB\)). Đường thẳng \(QF\) cắt đường tròn \(\left( O \right)\) tại điểm \(K\) (K khác Q). Chứng minh 3 điểm \(P,\,\,K,\,\,M\) thẳng hàng. Xét tam giác \(FDK\) và tam giác \(FQE\) có: \(\angle KFD = \angle EFQ\) (đối đỉnh); \(\angle FKD = \angle FEQ\) (hai góc nội tiếp cùng chắn cung \(DQ\));
Từ (3) và (4) \( \Rightarrow FI.FM = FK.FQ \Leftrightarrow \dfrac{{FM}}{{FQ}} = \dfrac{{FK}}{{FI}}\). Xét tam giác \(FMQ\) và tam giác \(FKI\) có: \(\dfrac{{FM}}{{FQ}} = \dfrac{{FK}}{{FI}}\,\,\left( {cmt} \right);\) \(\angle MFQ = \angle KFI\) (đối đỉnh); Tứ giác \(KIQM\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau). \( \Rightarrow \angle MKQ = \angle MIQ\) (hai góc nội tiếp cùng chắn cung \(MQ\)). Theo (*) ta đã chứng minh được \(\angle MBF = \angle CIF \Rightarrow \angle MBC = \angle MIF \Rightarrow \) Tứ giác \(MBIC\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau). Mà \(MOBC\) là tứ giác nội tiếp \( \Rightarrow M,\,\,B,\,\,O,\,\,I,\,\,C\) cùng thuộc 1 đường tròn. Ta có \(\angle OBM = {90^0}\,\,\left( {gt} \right) \Rightarrow OM\) là đường kính của đường tròn đi qua 5 điểm \(M,\,\,B,\,\,O,\,\,I,\,\,C\). \( \Rightarrow \angle OIM = {90^0}\) (góc nội tiếp chắn nửa đường tròn). \( \Rightarrow IM \bot OI \Rightarrow \angle MIQ = {90^0}\). Từ (5) \( \Rightarrow \angle MKQ = \angle MIQ = {90^0}\). Lại có \(\angle QKP = {90^0}\) (góc nội tiếp chắn nửa đường tròn). Từ đó ta có: \(\angle MKP = \angle MKQ + \angle QKP = {90^0} + {90^0} = {180^0}\). Vậy 3 điểm \(P,\,\,K,\,\,M\) thẳng hàng.
|




















Danh sách bình luận