Đề thi vào 10 môn Toán Lào Cai năm 2022Tải vềCâu 1 (1,0 điểm) Tính giá trị các biểu thức sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
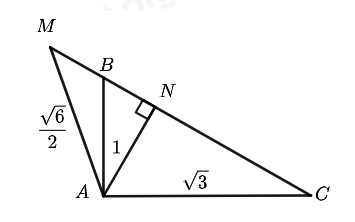
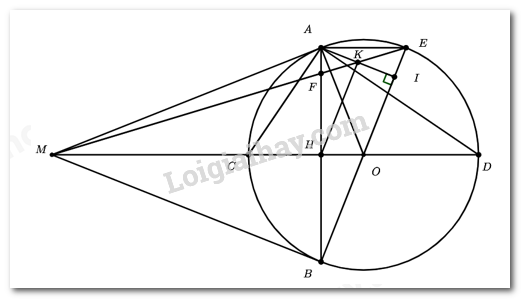
Đề bài Câu 1 (1,0 điểm) Tính giá trị các biểu thức sau: a) \(2 + \sqrt {36} \) b) \(\sqrt {25} - \sqrt 9 \) Câu 2 (1,5 điểm) Cho biểu thức \(P = \left( {\frac{1}{{\sqrt x + 1}} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x }}{{\sqrt x - 1}}\) (với \(x > 0,\,\,x \ne 1\)) a) Rút gọn biểu thức P. b) Tìm các giá trị của x để \(P = \frac{1}{2}\). Câu 3 (2,5 điểm) a) Giải phương trình: \({x^2} + 2x - 8 = 0\). b) Tìm các giá trị của tham số k để đường thẳng \({d_1}:y = \left( {k - 1} \right)x + k\) song song với đường thẳng \({d_2}:y = 3x - 12\). c) Tìm các giá trị của tham số m để đường thẳng \(d:y = - x + m + 1\) cắt Parabol \(\left( P \right):y = {x^2}\) tại hai điểm phân biệt có hoành độ \({x_1},{x_2}\) thỏa mãn điều kiện: \(x_1^2 - {x_2} - 4m + 1 = 0\). Câu 4 (1,5 điểm) a) Giải hệ phương trình: \(\left\{ \begin{array}{l}x + y = - 1\\2x - y = 4\end{array} \right.\) b) Hai ô tô xuất phát cùng một thời điểm từ địa điểm A đến địa điểm B với vận tốc mỗi ô tô không đổi. Sau 1 giờ quãng đường đi được của ô tô thứ nhất nhiều hơn quãng đường đi được của ô tô thứ hai là 5 km. Quãng đường đi được của ô tô thứ hai sau 3 giờ nhiều hơn quãng đường đi được của ô tô thứ nhất sau 2 giờ là 35 km. Tính vận tốc mỗi ô tô. Câu 5 (0,5 điểm) Chọn ngẫu nhiên một số trong các số tự nhiên từ \(1\) đến 10. Tính xác suất để số được chọn là số chia hết cho 5. Câu 6 (1,0 điểm) Cho tam giác ABC vuông tại A, độ dài các cạnh góc vuông: \(AB = 1,AC = \sqrt 3 \) a) Tính độ dài cạnh BC. b) Trên tia đối của tia BC lấy điểm M sao cho \(AM = \frac{{\sqrt 6 }}{2}\). Tính số đo góc \(\angle AMC\). Câu 7 (2,0 điểm) Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ hai tiếp tuyến phân biệt MA, MB đến đường tròn ( A, B là các tiếp điểm). a) Chứng minh tứ giác MAOB nội tiếp. b) Đường thẳng MO cắt đường tròn (O) lần lượt tại hai điểm C, D phân biệt sao cho MC < MD . Chứng minh: MA.DA= MD.AC. c) Đường thẳng BO cắt đường tròn (O) tại điểm thứ hai là E. Kẻ AI vuông góc với BE tại I. Đường thẳng ME cắt AI tại K, đường thẳng MO cắt AB tại H . Chứng minh hai đường thẳng HK và BE song song. Lời giải Câu 1 (TH): Phương pháp: Dùng công thức khai phương của căn bậc hai Cách giải: a) \(2 + \sqrt {36} \) Ta có: \(2 + \sqrt {36} = 2 + \sqrt {{6^2}} = 2 + 6 = 8\). b) \(\sqrt {25} - \sqrt 9 \) Ta có: \(\sqrt {25} - \sqrt 9 = \sqrt {{5^2}} - \sqrt {{3^2}} = 5 - 3 = 2\) Câu 2 (VD): Phương pháp: a) Tìm mẫu số chung, quy đồng, rút gọn P b) Giải phương trình \(P = \frac{1}{2}\) Cách giải: a) Với \(x > 0,\,\,x \ne 1\) ta có: \(\begin{array}{l}P = \left( {\frac{1}{{\sqrt x + 1}} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x }}{{\sqrt x - 1}}\\P = \frac{{\sqrt x - 1 + \sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}.\frac{{\sqrt x - 1}}{{\sqrt x }}\\P = \frac{{2\sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}.\frac{{\sqrt x - 1}}{{\sqrt x }}\\P = \frac{2}{{\sqrt x + 1}}\end{array}\) Vậy với \(x > 0,\,\,x \ne 1\) thì \(P = \frac{2}{{\sqrt x + 1}}\). b) Ta có: \(P = \frac{1}{2} \Leftrightarrow \frac{2}{{\sqrt x + 1}} = \frac{1}{2}\) \( \Leftrightarrow \sqrt x + 1 = 4 \Leftrightarrow \sqrt x = 3 \Leftrightarrow x = 9\,\,\left( {TMDK} \right)\). Vậy để \(P = \frac{1}{2}\) thì \(x = 9\). Câu 3 (VD): Phương pháp: a) Giải phương trình bằng công thức nghiệm b) \({d_1}\parallel d{ & _2} \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) c) Xét phương trình hoành độ giao điểm của (P) và (d), tìm điều kiện để phương trình có hai nghiệm phân biệt, áp dụng hệ thức Vi-et. Cách giải: a) Giải phương trình: \({x^2} + 2x - 8 = 0\). Ta có: \(\Delta ' = {1^2} - \left( { - 8} \right) = 9 > 0,\sqrt {\Delta '} = 3\) nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}x = - 1 + 3 = 2\\x = - 1 - 3 = - 4\end{array} \right.\) Vậy phương trình có tập nghiệm là \(S = \left\{ { - 4;2} \right\}\). b) Để \({d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}k - 1 = 3\\k \ne - 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = 4\\k \ne - 12\end{array} \right. \Leftrightarrow k = 4\) Vậy \(k = 4\). c) Xét phương trình hoành độ giao điểm của (P) và (d), ta có: \({x^2} = - x + m + 1 \Leftrightarrow {x^2} + x - m - 1 = 0\,\,\,\left( * \right)\) Ta có: \(\Delta = {1^2} - 4\left( { - m - 1} \right) = 1 + 4m + 4 = 4m + 5\) (P) cắt (d) tại hai điểm phân biệt có hoành độ \({x_1},{x_2} \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \({x_1},{x_2}\) \( \Leftrightarrow \Delta > 0 \Leftrightarrow 4m + 5 > 0 \Leftrightarrow m > \frac{{ - 5}}{4}\) Khi đó, theo hệ thức Vi – ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 1\\{x_1}{x_2} = - m - 1\end{array} \right.\) Lại có, \({x_1}\) là nghiệm của phương trình (*) nên ta có: \(x_1^2 = - {x_1} + m + 1\) Theo giả thiết: \(\begin{array}{l}\,\,\,\,\,\,\,\,x_1^2 - {x_2} - 4m + 1 = 0\\ \Leftrightarrow - {x_1} + m + 1 - {x_2} - 4m + 1 = 0\\ \Leftrightarrow - \left( {{x_1} + {x_2}} \right) - 3m + 2 = 0\\ \Leftrightarrow - \left( { - 1} \right) - 3m + 2 = 0\\ \Leftrightarrow 3 - 3m = 0\\ \Leftrightarrow - 3m = - 3\\ \Leftrightarrow m = 1\,\,\,\left( {tm} \right)\end{array}\) Vậy \(m = 1\). Câu 4 (VD): Phương pháp: a) Giải hệ phương trình bằng phương pháp cộng đại số. b) Gọi vận tốc của ô tô thứ nhất là \(x\) (km/h) \(\left( {x > 5} \right)\). Biểu diễn quãng đường của 2 xe theo x và lập phương trình về quãng đường. Cách giải: a) Ta có: \(\left\{ \begin{array}{l}x + y = - 1\\2x - y = 4\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3x = 3\\y = - 1 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1 - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 2\end{array} \right.\) Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {1; - 2} \right)\). b) Gọi vận tốc của ô tô thứ nhất là \(x\) (km/h) \(\left( {x > 5} \right)\). Vì sau 1 giờ quãng đường đi được của ô tô thứ nhất nhiều hơn quãng đường đi được của ô tô thứ hai là 5 km nên vận tốc của ô tô thứ hai là \(x - 5\) (km/h) Quãng đường đi được của ô tô thứ nhất sau 2 giờ là \(2x\) (km) Quãng đường đi được của ô tô thứ hai sau 3 giờ là \(3\left( {x - 5} \right)\) (km) Vì quãng đường đi được của ô tô thứ hai sau 3 giờ nhiều hơn quãng đường đi được của ô tô thứ nhất sau 2 giờ là 35 km nên ta có phương trình: \(3\left( {x - 5} \right) - 2x = 35\) \( \Leftrightarrow 3x - 15 - 2x = 35\) \( \Leftrightarrow x - 15 = 35\) \( \Leftrightarrow x = 35 + 15 = 50\) (tmđk) Vận tốc của ô tô thứ hai là \(50 - 5 = 45\) (km/h). Vậy vận tốc của ô tô thứ nhất là \(50\)km/h; vận tốc của ô tô thứ hai là \(45\) km/h. Câu 5 (VD): Phương pháp: Xác suất để chọn được 1 số chia hết cho 5 bằng tỉ số của số các số chia hết cho 5 và số các số bất kì trong các số tự nhiên từ \(1\) đến \(10\). Cách giải: Các số tự nhiên từ 1 đến 10 là \(\left\{ {1;2;3;4;5;6;7;8;9;10} \right\}\). Tập này gồm \(10\) số. Trong đó, số chia hết cho \(5\) là \(\left\{ {5;10} \right\}\). Tập này gồm 2 số. Xác suất để chọn được 1 số chia hết cho 5 là: \(\frac{2}{{10}} = \frac{1}{5} = 0,2\). Câu 6 (VD): Phương pháp: a) Dùng định lý Pythago b) Kẻ đường cao AN của \(\Delta ABC\) tính AH và tính \(\sin \angle AMN\) Cách giải: a) Áp dụng Pythago ta có \(B{C^2} = A{B^2} + A{C^2} = {1^2} + {\left( {\sqrt 3 } \right)^2} = 4 \Rightarrow BC = 2\) b) Kẻ đường cao AN của \(\Delta ABC\). Khi đó ta có \(AN.BC = AC.AB \Rightarrow AN = \frac{{\sqrt 3 }}{2}\) (hệ thức lượng) Xét \(\Delta ANM\) vuông tại N nên \(\sin \angle AMN = \frac{{AN}}{{AM}} = \frac{{\frac{{\sqrt 3 }}{2}}}{{\frac{{\sqrt 6 }}{2}}} = \frac{1}{{\sqrt 2 }} \Rightarrow \angle AMN = {45^0}\). Câu 7 (VD): Phương pháp: a) Dùng tổng hai góc đối diện bằng \({180^0}\) b) Chứng minh \(\Delta MAC = \Delta MDA\left( {g.g} \right)\) c) Chứng minh \(AF\) là phân giác của \(\angle MAK\) và \(\frac{{AK}}{{BM}} = \frac{{KI}}{{BM}} \Rightarrow AK = KI\). Cách giải: a) Do MA, MB là tiếp tuyến nên \(\angle MAO = \angle MBO = {90^0}\) Xét tứ giác AMBO có \(\angle MAO + \angle MBO = {90^0} + {90^0} = {180^0}\) Mà hai góc này ở vị trí đối diện nên tứ giác AMBO nội tiếp b) MA.DA= MD.AC. Xét \(\Delta MAC\) và \(\Delta MDA\) có \(\angle AMD\) chung \(\angle MAC = \angle MDA\) (góc nội tiếp và góc tọa bởi tiếp tuyến và dây cung cùng chắn cung ) Suy ra \(\Delta MAC = \Delta MDA\left( {g.g} \right) \Rightarrow \frac{{MA}}{{MD}} = \frac{{AC}}{{AD}} \Rightarrow MA.AD = MD.AC\) (đpcm) c) Ta có Mà \(\angle AEB = \angle IAB\) (do cùng phụ \(\angle EAI\)) \( \Rightarrow \angle MAB = \angle BAI\) \( \Rightarrow AF\) là phân giác của \(\angle MAK\) Mà \(AF \bot AE \Rightarrow AE\) là phân giác ngoài của \(\angle MAK\) Khi đó ta có \(\frac{{EK}}{{EM}} = \frac{{FK}}{{FM}} = \frac{{AK}}{{AM}}\) (t/c tia phân giác) Ta có \(\frac{{FK}}{{FM}} = \frac{{AK}}{{AM}} \Rightarrow \frac{{FK}}{{FM}} = \frac{{AK}}{{AB}}\) (1) Do \(\left\{ \begin{array}{l}KI \bot BE\\BM \bot BE\end{array} \right. \Rightarrow KI\parallel MB\) \( \Rightarrow \frac{{KE}}{{EM}} = \frac{{KI}}{{BM}}\) (Ta-let) (2) Từ (1) và (2) suy ra \(\frac{{AK}}{{BM}} = \frac{{KI}}{{BM}} \Rightarrow AK = KI\) Suy ra K là trung điểm của AI. Ta có \(\left\{ \begin{array}{l}OA = OB\\MA = MB\end{array} \right. \Rightarrow MO\) là trung trực của AB nên H là trung điểm AB Suy ra HK là đường trung bình của \(\Delta ABI\)\( \Rightarrow HK\parallel BE\) (đpcm)
|




















Danh sách bình luận