Đề thi vào 10 môn Toán Huế năm 2020

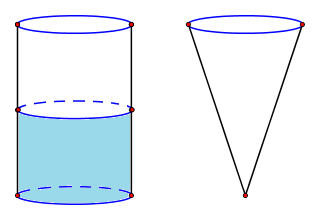
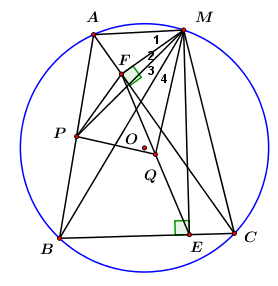
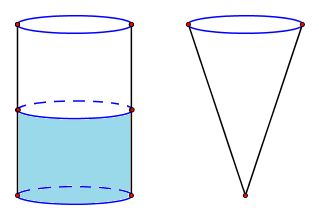
Đề bài

Câu 1:

a) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức \(A = \sqrt {25}  - \sqrt {16} \)

b) Đưa thừa số ra ngoài dấu căn, tính giá trị của biểu thức \(B = \sqrt {9.2}  - 2\sqrt {25.2}  + 2\sqrt {16.2} \)

c) Rút gọn biểu thức \(C = \left( {\dfrac{{\sqrt x  - 1}}{{x - \sqrt x }} - \dfrac{{\sqrt x }}{{x + \sqrt x }}} \right):\left( {1 - \dfrac{1}{{\sqrt x }}} \right)\)  với \(x > 0\) và \(x \ne 1.\)

Câu 2:

a) Không sử dụng máy tính cầm tay, giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\3y - 2x =  - 5\end{array} \right.\).

b) Tìm giá trị của \(m\) để đường thẳng \(y = mx + 2m\,\,\left( {m \ne 0} \right)\) song song với đường thẳng \(y = 2x + 2020\).

Câu 3:

Để xây dựng thành phố Huế ngày càng đẹp hơn và khuyến khích người dân rèn luyện sức khỏe, Ủy ban nhân dân tỉnh Thừa Thiên Huế đã cho xây dựng tuyến đường đi bộ ven bờ Bắc sông Hương, từ cầu Trường Tiền đến cầu Dã Viên có chiều dài 2km. Một người đi bộ trên tuyến đường này, khởi hành từ cầu Trường Tiền đến cầu Dã Viên rồi quay về lại cầu Trường Tiền hết tất cả \(\dfrac{{17}}{{18}}\) giờ. Tính vận tốc của người đó lúc về, biết rằng vận tốc lúc đi lớn hơn vận tốc lúc về là 0,5km/h.

Câu 4:

Cho phương trình \({x^2} - \left( {m + 1} \right)x + m = 0\)  (1) (với \(x\) là ẩn số)

a) Giải phương trình (1) khi \(m = 2.\)

b) Chứng minh phương trình (1) luôn có nghiệm với mọi giá trị của \(m\).

c) Tìm các giá trị của \(m\) để phương trình (1) có nghiệm \({x_1},{x_2}\) thỏa mãn điều kiện: \(x_1^2{x_2} + {x_1}x_2^2 - 12 = 0\).

Câu 5:

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Gọi M là một điểm bất kì trên cung nhỏ AC sao cho \(\angle BCM\) nhọn (M không trùng A và C). Gọi E và F lần lượt là chân các đường vuông góc kẻ từ M đến BC và AC. Gọi P là trung điểm của AB, Q là trung điểm của FE. Chứng minh rằng:

a) Tứ giác MFEC nội tiếp.

b) Tam giác FEM và tam giác ABM đồng dạng.

c) \(MA.MQ = MP.MF\) và \(\angle PQM = {90^0}\)

Câu 6: 

Một chiếc cốc thủy tinh có dạng hình trụ, chiều cao bằng 10cm và chứa một lượng nước có thể tích bằng một nửa thể tích của chiếc cốc. Một chiếc cốc thủy tinh khác có dạng hình nón (không chứa gì cả) và có bán kính đáy bằng bán kính đáy chiếc cốc hình trụ đã cho (hình vẽ bên). Biết rằng khi đổ hết lượng nước trong chiếc cốc hình trụ vào chiếc cốc hình nón thì chiếc cốc hình nón đầy nước và không có nước tràn ra ngoài. Tính chiều cao của chiếc cốc có dạng hình nón (bỏ qua bề dày của thành cốc và đáy cốc). 

Lời giải chi tiết

Câu 1 (1,5 điểm)

Cách giải:

a) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức \(A = \sqrt {25}  - \sqrt {16} \)

Ta có: \(A = \sqrt {25}  - \sqrt {16} \)\( = 5 - 4 = 1\)

Vậy \(A = 1.\)

b) Đưa thừa số ra ngoài dấu căn, tính giá trị của biểu thức \(B = \sqrt {9.2}  - 2\sqrt {25.2}  + 2\sqrt {16.2} \)

Ta có: \(B = \sqrt {9.2}  - 2\sqrt {25.2}  + 2\sqrt {16.2} \)

\(\begin{array}{l} = \sqrt {{3^2}.2}  - 2\sqrt {{5^2}.2}  + 2\sqrt {{4^2}.2} \\ = 3\sqrt 2  - 2.5\sqrt 2  + 2.4\sqrt 2 \\ = 3\sqrt 2  - 10\sqrt 2  + 8\sqrt 2 \\ = \sqrt 2 \left( {3 - 10 + 8} \right) = \sqrt 2 .1 = \sqrt 2 \end{array}\)

Vậy \(B = \sqrt 2 .\)

c) Rút gọn biểu thức \(C = \left( {\dfrac{{\sqrt x  - 1}}{{x - \sqrt x }} - \dfrac{{\sqrt x }}{{x + \sqrt x }}} \right):\left( {1 - \dfrac{1}{{\sqrt x }}} \right)\)  với \(x > 0\) và \(x \ne 1.\)

Với \(x > 0;x \ne 1\) ta có:

\(\begin{array}{l}C = \left( {\dfrac{{\sqrt x  - 1}}{{x - \sqrt x }} - \dfrac{{\sqrt x }}{{x + \sqrt x }}} \right):\left( {1 - \dfrac{1}{{\sqrt x }}} \right)\\ = \left( {\dfrac{{\sqrt x  - 1}}{{\sqrt x \left( {\sqrt x  - 1} \right)}} - \dfrac{{\sqrt x }}{{\sqrt x \left( {\sqrt x  + 1} \right)}}} \right):\left( {\dfrac{{\sqrt x  - 1}}{{\sqrt x }}} \right)\\ = \left( {\dfrac{1}{{\sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{\sqrt x }}\\ = \dfrac{{\sqrt x  + 1 - \sqrt x }}{{\sqrt x \left( {\sqrt x  + 1} \right)}}.\dfrac{{\sqrt x }}{{\sqrt x  - 1}}\\ = \dfrac{1}{{\sqrt x \left( {\sqrt x  + 1} \right)}}.\dfrac{{\sqrt x }}{{\sqrt x  - 1}}\\ = \dfrac{1}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} = \dfrac{1}{{x - 1}}\end{array}\)

Vậy \(C = \dfrac{1}{{x - 1}}\) với \(x \ge 0;x \ne 1\).

Câu 2 (1,5 điểm)

Cách giải:

a) Không sử dụng máy tính cầm tay, giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\3y - 2x =  - 5\end{array} \right.\).

\(\left\{ \begin{array}{l}x - y = 3\\3y - 2x =  - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 2y = 6\\ - 2x + 3y =  - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = y + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 4\end{array} \right.\)

Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {4;1} \right)\).

b) Tìm giá trị của \(m\) để đường thẳng \(y = mx + 2m\,\,\left( {m \ne 0} \right)\) song song với đường thẳng \(y = 2x + 2020\).

Để đường thẳng \(y = mx + 2m\,\,\left( {m \ne 0} \right)\) song song với đường thẳng \(y = 2x + 2020\) thì

\(\left\{ \begin{array}{l}m = 2\\2m \ne 2020\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 2\\m \ne 1010\end{array} \right. \Leftrightarrow m = 2\,\,\left( {tm} \right)\).

Vậy \(m = 2\).

Câu 3 (1,5 điểm)

Cách giải:

Để xây dựng thành phố Huế ngày càng đẹp hơn và khuyến khích người dân rèn luyện sức khỏe, Ủy ban nhân dân tỉnh Thừa Thiên Huế đã cho xây dựng tuyến đường đi bộ ven bờ Bắc sông Hương, từ cầu Trường Tiền đến cầu Dã Viên có chiều dài 2km. Một người đi bộ trên tuyến đường này, khởi hành từ cầu Trường Tiền đến cầu Dã Viên rồi quay về lại cầu Trường Tiền hết tất cả \(\dfrac{{17}}{{18}}\) giờ. Tính vận tốc của người đó lúc về, biết rằng vận tốc lúc đi lớn hơn vận tốc lúc về là 0,5km/h.

Gọi vận tốc lúc về của người đó là \(x\) (km/h) (ĐK: \(x > 0\)).

\( \Rightarrow \) Vận tốc lúc đi là \(x + 0,5\) (km/h).

Thời gian lúc đi là: \(\dfrac{2}{{x + 0,5}}\,\,\left( h \right)\).

Thời gian lúc về là \(\dfrac{2}{x}\,\,\left( h \right)\).

Vì người đó khởi hành từ cầu Trường Tiền đến cầu Dã Viên rồi quay về lại cầu Trường Tiền hết tất cả \(\dfrac{{17}}{{18}}\) giờ nên ta có phương trình:

     \(\dfrac{2}{{x + 0,5}} + \dfrac{2}{x} = \dfrac{{17}}{{18}}\)

\(\begin{array}{l} \Leftrightarrow 36x + 36\left( {x + 0,5} \right) = 17x\left( {x + 0,5} \right)\\ \Leftrightarrow 36x + 36x + 18 = 17{x^2} + \dfrac{{17}}{2}x\\ \Leftrightarrow 17{x^2} - \dfrac{{127}}{2}x - 18 = 0\\ \Leftrightarrow 34{x^2} - 127x - 36 = 0\\ \Leftrightarrow 34{x^2} - 136x + 9x - 36 = 0\\ \Leftrightarrow 34x\left( {x - 4} \right) + 9\left( {x - 4} \right) = 0\\ \Leftrightarrow \left( {x - 4} \right)\left( {34x + 9} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 4 = 0\\34x + 9 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\x =  - \dfrac{9}{{34}}\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)

Vậy vận tốc của người đó lúc về là 4km/h.

Câu 4 (2 điểm)

Cách giải:

Cho phương trình \({x^2} - \left( {m + 1} \right)x + m = 0\)  (1) (với \(x\) là ẩn số)

a) Giải phương trình (1) khi \(m = 2.\)

Với \(m = 2\) thì phương trình (1) trở thành

\(\begin{array}{l}\,\,\,\,\,\,\,\,{x^2} - 3x + 2 = 0\\ \Leftrightarrow {x^2} - x - 2x + 2 = 0\\ \Leftrightarrow x\left( {x - 1} \right) - 2\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array}\)

Vậy với \(m = 2\) thì phương trình (1) có hai nghiệm \(x = 1;\,\,x = 2.\)

b) Chứng minh phương trình (1) luôn có nghiệm với mọi giá trị của \(m\).

Xét phương trình \({x^2} - \left( {m + 1} \right)x + m = 0\)  (1)

Ta có: \(\Delta  = {\left[ { - \left( {m + 1} \right)} \right]^2} - 4.1.m\)

               \(\begin{array}{l} = {m^2} + 2m + 1 - 4m\\ = {m^2} - 2m + 1\\ = {\left( {m - 1} \right)^2}\end{array}\)

Vì \({\left( {m - 1} \right)^2} \ge 0\) với mọi \(m\) nên \(\Delta  \ge 0\) với mọi \(m\) .

Suy ra phương trình (1) luôn có nghiệm với mọi giá trị của \(m\).

c) Tìm các giá trị của \(m\) để phương trình (1) có nghiệm \({x_1},{x_2}\) thỏa mãn điều kiện: \(x_1^2{x_2} + {x_1}x_2^2 - 12 = 0\).

Theo câu b) ta có phương trình (1) luôn có nghiệm với mọi giá trị của \(m\).

Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình (1). Theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 1\\{x_1}{x_2} = m\end{array} \right.\).

Theo bài ra ta có:  \(x_1^2{x_2} + {x_1}x_2^2 - 12 = 0\)

\(\begin{array}{l} \Leftrightarrow {x_1}{x_2}\left( {{x_1} + {x_2}} \right) - 12 = 0\\ \Leftrightarrow m\left( {m + 1} \right) - 12 = 0\\ \Leftrightarrow {m^2} + m - 12 = 0\\ \Leftrightarrow {m^2} + 4m - 3m - 12 = 0\\ \Leftrightarrow m\left( {m + 4} \right) - 3\left( {m + 4} \right) = 0\\ \Leftrightarrow \left( {m + 4} \right)\left( {m - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 4 = 0\\m - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m =  - 4\\m = 3\end{array} \right.\end{array}\)

Vậy \(m =  - 4;\,\,m = 3\) thỏa mãn yêu cầu đề bài.

Câu 5 (VD)

Cách giải:

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Gọi M là một điểm bất kì trên cung nhỏ AC sao cho \(\angle BCM\) nhọn (M không trùng A và C). Gọi E và F lần lượt là chân các đường vuông góc kẻ từ M đến BC và AC. Gọi P là trung điểm của AB, Q là trung điểm của FE. Chứng minh rằng:

a) Tứ giác MFEC nội tiếp.

Ta có: \(MF \bot AC \Rightarrow \angle MFC = {90^0}\)

\(ME \bot BC \Rightarrow \angle MEC = {90^0}\)

Tứ giác \(MFEC\)  có \(\angle MFC = \angle MEC = {90^0}\) nên là tứ giác nội tiếp (hai đỉnh kề một cạnh cùng nhìn cạnh đối diện các góc bằng nhau) (đpcm).

b) Tam giác FEM và tam giác ABM đồng dạng.

Theo câu a, tứ giác \(MFEC\) nội tiếp nên \(\angle EFM + \angle ECM = {180^0}\) (tính chất)  (1)

Tứ giác \(ABCM\)  nội tiếp nên \(\angle BAM + \angle BCM = {180^0}\) (tính chất) (2)

Từ (1) và (2) \( \Rightarrow \angle BAM = \angle EFM\) (cùng bù với \(\angle BCM\))

\(\angle FEM = \angle FCM\) (hai góc nội tiếp cùng chắn cung \(FM\))  (3)

\(\angle FCM = \angle ABM\) (hai góc nội tiếp cùng chắn cung \(AM\))  (4)

Từ (3) và (4) suy ra \(\angle FEM = \angle ABM\)

Xét \(\Delta FEM\) và \(\Delta ABM\) có:

\(\begin{array}{l}\angle BAM = \angle EFM\,\,\,\left( {cmt} \right)\\\angle FEM = \angle ABM\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta FEM \sim \Delta ABM\left( {g - g} \right)\,\,\,\left( {dpcm} \right)\end{array}\)

c) \(MA.MQ = MP.MF\) và \(\angle PQM = {90^0}\)

Từ câu b ta có: \(\Delta FEM \sim \Delta ABM\) \( \Rightarrow \dfrac{{FE}}{{AB}} = \dfrac{{MF}}{{MA}}\) (các cặp cạnh tương ứng tỉ lệ)

\( \Rightarrow \dfrac{{2FQ}}{{2AP}} = \dfrac{{MF}}{{MA}} \Rightarrow \dfrac{{FQ}}{{AP}} = \dfrac{{MF}}{{MA}}\) \( \Rightarrow \dfrac{{AM}}{{AP}} = \dfrac{{FM}}{{FQ}}\)

Xét \(\Delta MAP\) và \(\Delta MFQ\) có:

\(\begin{array}{l}\dfrac{{AM}}{{AP}} = \dfrac{{FM}}{{FQ}}\\\angle MAP = \angle MFQ\,\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta MAP \sim \Delta MFQ\,\,\,\,\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow \dfrac{{MA}}{{MF}} = \dfrac{{MP}}{{MQ}}\) (các cặp cạnh tương ứng tỉ lệ)

\( \Rightarrow MA.MQ = MP.MF\) (đpcm)

Lại có \(\Delta MAP \sim \Delta MFQ\,\,\,\left( {cmt} \right)\)\( \Rightarrow \angle AMP = \angle FMQ\) (hai góc tương ứng)

\(\begin{array}{l} \Rightarrow \angle {M_1} + \angle {M_2} = \angle {M_2} + \angle {M_3} + \angle {M_4}\\ \Rightarrow \angle {M_1} = \angle {M_3} + \angle {M_4}\\ \Rightarrow \angle AMF = \angle PMQ\end{array}\)

Xét \(\Delta MAF\) và \(\Delta MPQ\) có:

\(\begin{array}{l}\angle AMF = \angle PMQ\left( {cmt} \right)\\\dfrac{{MA}}{{MF}} = \dfrac{{MP}}{{MQ}}\left( {cmt} \right)\\ \Rightarrow \Delta MAF \sim \Delta MPQ\,\,\,\,\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow \angle MFA = \angle MQP\) (hai góc tương ứng)

Mà \(\angle MFA = {90^0}\) nên \(\angle MQP = {90^0}\)  (đpcm).

Câu 6 (1,0 điểm)

Cách giải:

Một chiếc cốc thủy tinh có dạng hình trụ, chiều cao bằng 10cm và chứa một lượng nước có thể tích bằng một nửa thể tích của chiếc cốc. Một chiếc cốc thủy tinh khác có dạng hình nón (không chứa gì cả) và có bán kính đáy bằng bán kính đáy chiếc cốc hình trụ đã cho (hình vẽ bên). Biết rằng khi đổ hết lượng nước trong chiếc cốc hình trụ vào chiếc cốc hình nón thì chiếc cốc hình nón đầy nước và không có nước tràn ra ngoài. Tính chiều cao của chiếc cốc có dạng hình nón (bỏ qua bề dày của thành cốc và đáy cốc).

Theo đề bài ta có:

Thể tích nước trong cốc hình trụ = Thể tích chiếc cốc hình nón = \(\dfrac{1}{2}\) thể tích chiếc cốc hình trụ.

Gọi bán kính đáy của hai chiếc cốc là: \(R\,\,\,\left( {R > 0} \right)\).

Chiều cao của chiếc cốc hình trụ là \(h = 10\,\,cm\,\,\,\left( {gt} \right).\)

Gọi chiều cao của chiếc cốc hình nón là \({h_1}\,\,\left( {{h_1} > 0} \right).\) 

Gọi thể tích chiếc cốc hình trụ là \(V,\) thể tích chiếc cốc hình nón là \({V_1}.\)

\(\begin{array}{l} \Rightarrow {V_1} = \dfrac{1}{2}V \Leftrightarrow \dfrac{1}{3}\pi {R^2}{h_1} = \dfrac{1}{2}\pi {R^2}h\\ \Leftrightarrow \dfrac{1}{3}{h_1} = \dfrac{1}{2}.10 \Leftrightarrow {h_1} = 15\,\,cm\,\,\left( {tm} \right).\end{array}\)

Vậy chiều cao của chiếc cốc hình nón là \(15\,\,cm.\)