Đề thi vào 10 môn Toán Vĩnh Phúc năm 2019Tải vềI. PHẦN TRẮC NGHIỆM (2 điểm) Câu 1: Cho khối hộp chữ nhật có chiều dài 3 m, chiều rộng 2 m và chiều cao 1m. Thể tích khối hộp đã cho bằng: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài I. PHẦN TRẮC NGHIỆM (2 điểm) Câu 1: Cho khối hộp chữ nhật có chiều dài 3 m, chiều rộng 2 m và chiều cao 1m. Thể tích khối hộp đã cho bằng: A. \(3{m^3}\) B. \(6{m^3}\) C. \(2{m^3}\) D. \(12{m^3}\) Câu 2: Biểu thức \(P = \sqrt 5 \left( {\sqrt {10} - \sqrt {40} } \right)\) có giá trị bằng: A. \( - 5\sqrt {10} \) B. \( - 5\sqrt 6 \) C. \( - 5\sqrt {30} \) D. \( - 5\sqrt 2 \) Câu 3: Tổng tất cả các nghiệm của phương trình \({x^2} - 6x + 1 = 0\) bằng: A. \(6\) B. \( - 3\) C. \(3\) D. \( - 6\) Câu 4: Tìm tất cả các giá trị của \(x\) để biểu thức \(P = \sqrt {x - 2} \) xác định. A. \(x < 2\) B. \(x > 2\) C. \(x \ge 2\) D. \(x \le 2\) II. PHẦN TỰ LUẬN (8 điểm) Câu 5 (1 điểm) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 3\\x + y = 6\end{array} \right..\) Câu 6 (2 điểm) Cho \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\,\,y = - x + m\) (\(x\) là ẩn, \(m\) là tham số). a) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) khi \(m = 4.\) b) Tìm tất cả các giá trị của \(m\) để đường thẳng \(\left( d \right)\) cắt parabol \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_1};\,\,{y_1}} \right),\,\,B\left( {{x_2},\,\,{y_2}} \right)\) thỏa mãn \({x_1}{x_2} + {y_1}{y_2} = 5.\) Câu 7 (1 điểm) Người thứ nhất đi đoạn đường từ địa điểm A đến địa điểm B cách nhau 78 km. Sau khi người thứ nhất đi được 1 giờ thì người thứ hai đi theo chiều ngược lại vẫn trên đoạn đường đó từ B về A. Hai người gặp nhau ở địa điểm C cách B một quãng đường 36 km. Tính vận tốc của mỗi người, biết rằng vận tốc của người thứ hai lớn hơn vận tốc của người thứ nhất là 4 km/h và vận tốc của mỗi người trong suổ đoạn đường là không thay đổi. Câu 8 (3,0 điểm): Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Gọi \(M\) là một điểm di động trên cung nhỏ \(BC\) của đường tròn \(\left( O \right)\) (\(M\) không trình với \(B,C\)). Gọi \(H,K,D\) theo thứ tự là chân các đường vuông góc kẻ từ \(M\) đến các đường thẳng \(AB,AC,BC\). a) Chứng minh tứ giác \(AHMK\) nội tiếp đường tròn. b) Chứng minh \(MH.MC = MK.MB\). c) Tìm vị trí của điểm \(M\) để \(DH + DK\) lớn nhất. Câu 9 (1,0 điểm): Cho ba số thực dương \(a,b,c\). Chứng minh: \(\dfrac{{2 + 6a + 3b + 6\sqrt {2bc} }}{{2a + b + 2\sqrt {2bc} }} \ge \dfrac{{16}}{{\sqrt {2{b^2} + 2{{\left( {a + c} \right)}^2}} + 3}}\) Lời giải chi tiết I. PHẦN TRẮC NGHIỆM (2 điểm)
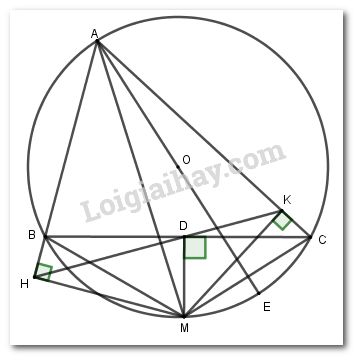
Câu 1 Phương pháp: Thể tích hình hộp chữ nhật có các kích thước \(a,\,\,b,\,\,c\) là: \(V = abc.\) Cách giải: Thể tích hình hộp chữ nhật cần tính là: \(V = 3.2.1 = 6{m^3}.\) Chọn B. Câu 2 Phương pháp: Sử dụng các công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B ;\,\,\,\sqrt {AB} = \sqrt A .\sqrt B .\) Cách giải: \(\begin{array}{l}P = \sqrt 5 \left( {\sqrt {10} - \sqrt {40} } \right) = \sqrt 5 \left( {\sqrt {10} - \sqrt {4.10} } \right) = \sqrt 5 \left( {\sqrt {10} - 2\sqrt {10} } \right)\\ = \sqrt 5 .\left( { - \sqrt {10} } \right) = - \sqrt 5 .\sqrt {10} = - \sqrt {5.10} = - \sqrt {50} = - \sqrt {25.2} = - 5\sqrt 2 .\end{array}\) Chọn D. Câu 3 Phương pháp: Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thì \({x_1} + {x_2} = - \dfrac{b}{a}.\) Cách giải: Tổng hai nghiệm của phương trình \({x^2} - 6x + 1 = 0\) là: \({x_1} + {x_2} = 6.\) Chọn A. Câu 4 Phương pháp: Biểu thức: \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\) Cách giải: Biểu thức \(P = \sqrt {x - 2} \) xác định \( \Leftrightarrow x - 2 \ge 0 \Leftrightarrow x \ge 2.\) Chọn C. II. PHẦN TỰ LUẬN (8 điểm) Câu 5 Phương pháp: Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số. Cách giải: \(\left\{ \begin{array}{l}x - 2y = 3\\x + y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3y = 3\\x = 6 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 5\end{array} \right..\) Vậy hệ phương trình có nghiệm là: \(\left( {x;\,\,y} \right) = \left( {5;\,\,1} \right).\) Câu 6 Phương pháp: a) Thay \(m = 4\) và phương trình hoành độ giao điểm của hai đồ thị hàm số. Giải phương trình rồi kết luận. b) Đường thẳng \(d\) cắt \(\left( P \right)\) tại hai điểm \( \Leftrightarrow \) phương trình hoành độ giao điểm có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\) Áp dụng định lý Vi-et và hệ thức bài cho để tìm \(m.\) Cách giải: Phương trình hoành độ giao điểm của hai đồ thị hàm số là: \(\dfrac{1}{2}{x^2} = - x + m \Leftrightarrow {x^2} + 2x - 2m = 0\,\,\,\left( * \right)\) a) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) khi \(m = 4.\) Với \(m = 4 \Rightarrow \left( * \right) \Leftrightarrow {x^2} + 2x - 8 = 0 \Leftrightarrow \left( {x - 2} \right)\left( {x + 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 4\end{array} \right.\) +) Với \(x = 2 \Rightarrow y = \dfrac{1}{2}{.2^2} = 2 \Rightarrow M\left( {2;\,\,2} \right).\) +) Với \(x = - 4 \Rightarrow y = \dfrac{1}{2}.{\left( { - 4} \right)^2} = 8 \Rightarrow N\left( { - 4;\,\,8} \right).\) Vậy với \(m = 4\) thì \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(M\left( {2;\,\,2} \right),\,\,N\left( { - 4;\,\,8} \right).\) b) Tìm tất cả các giá trị của \(m\) để đường thẳng \(\left( d \right)\) cắt parabol \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_1};\,\,{y_1}} \right),\,\,B\left( {{x_2},\,\,{y_2}} \right)\) thỏa mãn \({x_1}{x_2} + {y_1}{y_2} = 5.\) Số giao điểm của hai đồ thị hàm số là số nghiệm của phương trình \(\left( * \right).\) \( \Rightarrow \left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt\( \Leftrightarrow \Delta ' > 0 \Leftrightarrow 1 + 2m > 0 \Leftrightarrow m > - \dfrac{1}{2}.\) Đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_1};\,\,{y_1}} \right)\) và \(B\left( {{x_2};\,\,{y_2}} \right)\) \( \Rightarrow A\left( {{x_1};\,\, - {x_1} + m} \right);\,\,\,B\left( {{x_2}; - {x_2} + m} \right).\) \( \Rightarrow {x_1},\,\,{x_2}\) là hai nghiệm của phương trình \(\left( * \right).\) Áp dụng định lý Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}{x_2} = - 2m\end{array} \right..\) Theo đề bài ta có: \({x_1}{x_2} + {y_1}{y_2} = 5\) \(\begin{array}{l} \Leftrightarrow {x_1}{x_2} + \left( { - {x_1} + m} \right)\left( { - {x_2} + m} \right) = 5\\ \Leftrightarrow {x_1}{x_2} + {x_1}{x_2} - m\left( {{x_1} + {x_2}} \right) + {m^2} = 5\\ \Leftrightarrow - 2m - 2m - m.\left( { - 2} \right) + {m^2} = 5\\ \Leftrightarrow {m^2} - 2m - 5 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1 + \sqrt 6 \,\,\,\left( {tm} \right)\\m = 1 - \sqrt 6 \,\,\,\left( {ktm} \right)\end{array} \right..\end{array}\) Vậy \(m = 1 + \sqrt 6 \) thỏa mãn yêu cầu bài toán. Câu 7 Phương pháp: Gọi vận tốc của người thứ nhất là \(x\,\,\left( {km/h} \right),\,\,\left( {x > 0} \right).\) Khi đó vận tốc của người thứ hai là: \(x + 4\,\,\left( {km/h} \right).\) Biểu diễn các đại lượng chưa biết theo \(x\) và các đại lượng đã biết. Dựa vào các giả thiết bài toán để lập phương trình. Giải phương trình tìm \(x,\) đối chiếu với điều kiện rồi kết luận. Cách giải: Gọi vận tốc của người thứ nhất là \(x\,\,\left( {km/h} \right),\,\,\left( {x > 0} \right).\) Khi đó vận tốc của người thứ hai là: \(x + 4\,\,\left( {km/h} \right).\) Quãng đường người thứ nhất đi được cho đến khi gặp người thứ hai là: \(78 - 36 = 42\,\,\left( {km} \right).\) \( \Rightarrow \) Thời gian người thứ nhất đi đến khi gặp được người thứ hai là: \(\dfrac{{42}}{x}\) (giờ). Thời gian người thứ hai đi đến khi gặp người thứ nhất là: \(\dfrac{{36}}{{x + 4}}\) (giờ). Theo đề bài ta có: Người thức hai xuất phát sau người thứ nhất một giờ nên ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\,\dfrac{{42}}{{\,x}} - \dfrac{{36}}{{x + 4}} = 1 \Rightarrow 42\left( {x + 4} \right) - 36x = x\left( {x + 4} \right)\\ \Leftrightarrow 42x + 168 - 36x = {x^2} + 4x\\ \Leftrightarrow {x^2} - 2x - 168 = 0\\ \Leftrightarrow {x^2} - 14x + 12x - 168 = 0\\ \Leftrightarrow x\left( {x - 14} \right) + 12\left( {x - 14} \right) = 0\\ \Leftrightarrow \left( {x + 12} \right)\left( {x - 14} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 12 = 0\\x - 14 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 12\,\,\left( {ktm} \right)\\x = 14\,\,\left( {tm} \right)\end{array} \right..\end{array}\) Vậy vận tốc của người thứ nhất là \(14\,km/h\) và vận tốc của người thứ hai là: \(14 + 4 = 18\,km/h.\) Câu 8 Phương pháp: a) Chứng minh tứ giác có tổng hai góc đối diện bằng \({180^0}\). b) Chứng minh hai tam giác \(\Delta HBM\) và \(\Delta KCM\) đồng dạng suy ra các tỉ số tưng ứng. c) Chứng minh \(H,D,K\) thẳng hàng. Từ đó đánh giá GTLN của \(DH + DK\). Cách giải:
a) Ta có: \(\left. \begin{array}{l}MH \bot AB\left( {gt} \right) \Rightarrow \angle MHA = {90^0}\\MK \bot AC\left( {gt} \right) \Rightarrow \angle MKA = {90^0}\end{array} \right\} \Rightarrow \angle MHA + \angle MKA = {90^0} + {90^0} = {180^0}\). Mà hai góc này ở vị trí đối diện nên tứ giác \(AHMK\) nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)). b) Dễ thấy tứ giác \(ABMC\) nội tiếp \( \Rightarrow \angle HBM = \angle MCA\) (góc ngoài tại một đỉnh và góc trong đỉnh đối diện) Xét \(\Delta HBM\) và \(\Delta KCM\) có: \(\left. \begin{array}{l}\angle MHB = \angle MKC\left( { = {{90}^0}} \right)\\\angle HBM = \angle MCA\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta HBM \sim \Delta KCM\left( {g.g} \right)\) \( \Rightarrow \dfrac{{HM}}{{KM}} = \dfrac{{BM}}{{CM}}\) (cạnh tưng ứng) \( \Rightarrow MH.MC = MB.MK\) (đpcm). c) Nối \(D\) với \(H\), \(D\) với \(K\). Xét tứ giác \(BHMD\) có \(\angle BHM + \angle BDM = {90^0} + {90^0} = {180^0}\). Mà hai góc này ở vị trí đối diện nên \(BHDM\) là tứ giác nội tiếp \( \Rightarrow \angle BDH = \angle BMH\) (cùng chắn cung \(BH\)) (1) Xét tứ giác \(CKDM\) có \(\angle MDC = \angle MKC = {90^0}\) nên tứ giác \(CKDM\) nội tiếp (hai đỉnh kề nhau cùng nhìn một cạnh các góc bằng nhau) \( \Rightarrow \angle KDC = \angle KMC\) (cùng chắn cung \(KC\)) (2) Mà \(\Delta HBM \sim \Delta KCM\left( {cmt} \right) \Rightarrow \angle BMH = \angle KMC\) (góc tương ứng) (3) Từ \(\left( 1 \right)\), \(\left( 2 \right)\) và \(\left( 3 \right)\) suy ra \(\angle BDH = \angle KDC\) suy ra \(H,D,K\) thẳng hàng hay \(DH + DK = HK\). Ta có: \(\angle MHD = \angle MBD\) (cùng chắn cung \(MD\)) \( \Rightarrow \angle MHK = \angle MBC\) \(\angle MKD = \angle MCD\) (cùng chắn cung \(MD\)) \( \Rightarrow \angle MKH = \angle MCB\) Xét \(\Delta MHK\) và \(\Delta MBC\) có: \(\left. \begin{array}{l}\angle MHK = \angle MBC\left( {cmt} \right)\\\angle MKH = \angle MCB\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta MHK \sim \Delta MBC\left( {g.g} \right)\) \( \Rightarrow \dfrac{{MH}}{{MB}} = \dfrac{{MK}}{{MC}} = \dfrac{{HK}}{{BC}}\) (cạnh tương tứng) Mà \(MH \le MB,MK \le MC \Rightarrow \dfrac{{MH}}{{MB}} = \dfrac{{MK}}{{MC}} \le 1\) \( \Rightarrow \dfrac{{HK}}{{BC}} \le 1 \Rightarrow HK \le BC\) cố định. Dấu “=” xảy ra khi \(MH = MB,MK = MC\) hay \(H \equiv B,K \equiv C\) hay \(AB \bot BM,AC \bot CM\) \( \Rightarrow \angle ABM = \angle ACM = {90^0}\) hay \(A,B,C,M\) nằm trên đường tròn đường kính \(AM\). Kẻ đường kính \(AE\) của đường tròn tâm \(\left( O \right)\) thì \(M \equiv E\). Vậy \(\max \left( {DH + DK} \right) = BC\) khi \(M \equiv E\). Câu 9 Phương pháp: Đánh giá \(VT \ge \dfrac{{16}}{{a + b + c + 3}} \ge VP\) bằng cách sử dụng phối hợp các bất đẳng thức: + Bất đẳng thức Cô – si \(a + b \ge 2\sqrt {ab} \). + Bất đẳng thức phụ: \(\dfrac{{{a^2}}}{x} + \dfrac{{{b^2}}}{y} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{x + y}}\). Cách giải: Ta có: \(VT = \dfrac{{2 + 6a + 3b + 6\sqrt {2bc} }}{{2a + b + 2\sqrt {2bc} }} = \dfrac{{2 + 3\left( {2a + b + 2\sqrt {2bc} } \right)}}{{2a + b + 2\sqrt {2bc} }} = \dfrac{2}{{2a + b + 2\sqrt {2bc} }} + 3\) Mà \(2\sqrt {2bc} = 2\sqrt {b.2c} \le b + 2c\) (BĐT Cô – si) \(\begin{array}{l} \Rightarrow 2a + b + 2\sqrt {2bc} \le 2a + b + b + 2c = 2\left( {a + b + c} \right)\\ \Rightarrow \dfrac{2}{{2a + b + 2\sqrt {2bc} }} \ge \dfrac{2}{{2\left( {a + b + c} \right)}} = \dfrac{1}{{a + b + c}}\\ \Rightarrow \dfrac{2}{{2a + b + 2\sqrt {2bc} }} + 3 \ge \dfrac{1}{{a + b + c}} + 3 = \dfrac{{{1^2}}}{{a + b + c}} + \dfrac{{{3^2}}}{3} \ge \dfrac{{{{\left( {1 + 3} \right)}^2}}}{{a + b + c + 3}} = \dfrac{{16}}{{a + b + c + 3}}\end{array}\) \( \Rightarrow VT \ge \dfrac{{16}}{{a + b + c + 3}}\). Ta chứng minh \(VP \le \dfrac{{16}}{{a + b + c + 3}}\). Thật vậy, \(\begin{array}{l}\dfrac{{16}}{{\sqrt {2{b^2} + 2{{\left( {a + c} \right)}^2}} + 3}} \le \dfrac{{16}}{{a + b + c + 3}} \Leftrightarrow \sqrt {2{b^2} + 2{{\left( {a + c} \right)}^2}} + 3 \ge a + b + c + 3\\ \Leftrightarrow \sqrt {2{b^2} + 2{{\left( {a + c} \right)}^2}} \ge a + b + c \Leftrightarrow 2{b^2} + 2{\left( {a + c} \right)^2} \ge {\left( {a + b + c} \right)^2}\\ \Leftrightarrow 2{a^2} + 2{b^2} + 2{c^2} + 4ac \ge {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca\\ \Leftrightarrow {a^2} + {b^2} + {c^2} - 2ab - 2bc + 2ca \ge 0\end{array}\) \( \Leftrightarrow {\left( {b - a - c} \right)^2} \ge 0\) (luôn đúng). Do đó \(VP \le \dfrac{{16}}{{a + b + c + 3}}\), suy ra điều phải chứng minh. Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}b = 2c\\\dfrac{1}{{a + b + c}} = \dfrac{3}{3} = 1\\{\left( {b - a - c} \right)^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2c\\a + b + c = 1\\b - a - c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{4}\\b = \dfrac{1}{2}\\c = \dfrac{1}{4}\end{array} \right.\).
|




















Danh sách bình luận