Đề thi vào 10 môn Toán Thanh Hóa năm 2020Tải vềCâu I: Cho biểu thức Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
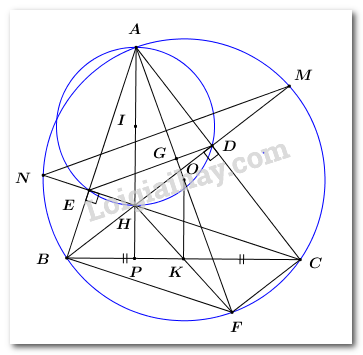
Đề bài Câu I: Cho biểu thức \(P = \left( {\dfrac{{4\sqrt x }}{{\sqrt x + 2}} - \dfrac{{8x}}{{x - 4}}} \right):\left( {\dfrac{{\sqrt x + 2}}{{\sqrt x - 2}} + 3} \right)\) với \(x \ge 0,\,\,x \ne 1\) và \(x \ne 4\). 1. Rút gọn biểu thức \(P\). 2. Tìm các giá trị của \(x\) để \(P = - 4\). Câu II: 1. Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(\left( d \right)\) có phương trình \(y = ax + b\). Tìm \(a,\,\,b\) để đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ bằng 2 và đi qua điểm \(M\left( {2;3} \right)\). 2. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 3y = 4\\2x - 3y = - 1\end{array} \right.\) Câu III: 1. Giải phương trình \({x^2} + 5x + 4 = 0\). 2. Cho phương trình \({x^2} + 5x + m - 2 = 0\) (\(m\) là tham số). Tìm các giá trị của \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,{x_2}\) thỏa mãn hệ thức \(\dfrac{1}{{{{\left( {{x_1} - 1} \right)}^2}}} + \dfrac{1}{{{{\left( {{x_2} - 1} \right)}^2}}} = 1\) Câu IV: Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Các đường cao \(BD,\,\,CE\) (\(D\) thuộc \(AC\), \(E\) thuộc \(AB\)) của tam giác kéo dài lần lượt cắt đường tròn \(\left( O \right)\) tại các điểm \(M\) và \(N\) (\(M\) khác \(B\), \(N\) khác \(C\)). 1. Chứng minh tứ giác \(BCDE\) nội tiếp được trong một đường tròn. 2. Chứng minh \(MN\) song song với \(DE\). 3. Khi đường tròn \(\left( O \right)\) và dây \(BC\) cố định, điểm \(A\) di động trên cung lớn \(BC\) sao cho tam giác \(ABC\) nhọn, chứng minh bán kính đường tròn ngoại tiếp tam giác \(ADE\) không đổi và tìm vị trí của điểm \(A\) để diện tích tam giác \(ADE\) đạt giá trị lớn nhất. Câu V: Cho ba số thực dương \(x,y,z\) thỏa mãn điều kiện \(x + y + z = xyz\). Tìm giá trị nhỏ nhất của biểu thức \(Q = \dfrac{{y + 2}}{{{x^2}}} + \dfrac{{z + 2}}{{{y^2}}} + \dfrac{{x + 2}}{{{z^2}}}\) Lời giải chi tiết Câu I (2,0 điểm) Cách giải: Cho biểu thức \(P = \left( {\dfrac{{4\sqrt x }}{{\sqrt x + 2}} - \dfrac{{8x}}{{x - 4}}} \right):\left( {\dfrac{{\sqrt x + 2}}{{\sqrt x - 2}} + 3} \right)\) với \(x \ge 0,\,\,x \ne 1\) và \(x \ne 4\). 1. Rút gọn biểu thức \(P\). Với \(x \ge 0,\,\,x \ne 1\) và \(x \ne 4\) ta có: \(\begin{array}{l}P = \left( {\dfrac{{4\sqrt x }}{{\sqrt x + 2}} - \dfrac{{8x}}{{x - 4}}} \right):\left( {\dfrac{{\sqrt x + 2}}{{\sqrt x - 2}} + 3} \right)\\P = \left( {\dfrac{{4\sqrt x }}{{\sqrt x + 2}} - \dfrac{{8x}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}} \right):\dfrac{{\sqrt x + 2 + 3\left( {\sqrt x - 2} \right)}}{{\sqrt x - 2}}\\P = \dfrac{{4\sqrt x \left( {\sqrt x - 2} \right) - 8x}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}:\dfrac{{\sqrt x + 2 + 3\sqrt x - 6}}{{\sqrt x - 2}}\\P = \dfrac{{4x - 8\sqrt x - 8x}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}:\dfrac{{4\sqrt x - 4}}{{\sqrt x - 2}}\\P = \dfrac{{ - 8\sqrt x - 4x}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}.\dfrac{{\sqrt x - 2}}{{4\left( {\sqrt x - 1} \right)}}\\P = \dfrac{{ - 4\sqrt x \left( {2 + \sqrt x } \right)}}{{\sqrt x + 2}}.\dfrac{1}{{4\left( {\sqrt x - 1} \right)}}\\P = \dfrac{{ - \sqrt x }}{{\sqrt x - 1}} = \dfrac{{\sqrt x }}{{1 - \sqrt x }}\end{array}\) 2. Tìm các giá trị của \(x\) để \(P = - 4\). Ta có: \(\begin{array}{l}P = - 4 \Leftrightarrow \dfrac{{\sqrt x }}{{1 - \sqrt x }} = - 4\\ \Leftrightarrow \sqrt x = - 4\left( {1 - \sqrt x } \right)\\ \Leftrightarrow \sqrt x = - 4 + 4\sqrt x \\ \Leftrightarrow 3\sqrt x = 4\\ \Leftrightarrow \sqrt x = \dfrac{4}{3}\\ \Leftrightarrow x = \dfrac{{16}}{9}\,\,\left( {tm} \right)\end{array}\) Vậy để \(P = - 4\) thì \(x = \dfrac{{16}}{9}\). Câu II (2,0 điểm) Cách giải: 1. Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(\left( d \right)\) có phương trình \(y = ax + b\). Tìm \(a,\,\,b\) để đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ bằng 2 và đi qua điểm \(M\left( {2;3} \right)\). Đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ bằng 2 nên đường thẳng \(\left( d \right)\) đi qua điểm \(\left( {0;2} \right)\). Thay tọa độ điểm \(\left( {0;2} \right)\) vào phương trình đường thẳng \(\left( d \right)\) ta có: \(2 = a.0 + b \Leftrightarrow b = 2\). Khi đó phương trình đường thẳng \(\left( d \right)\) có dạng \(y = ax + 2\). Đường thẳng \(\left( d \right)\) đi qua điểm \(M\left( {2;3} \right)\) nên thay tọa độ điểm \(M\) vào phương trình đường thẳng \(\left( d \right)\) ta có: \(3 = a.2 + 2 \Leftrightarrow 2a = 1 \Leftrightarrow a = \dfrac{1}{2}\). Vậy \(a = \dfrac{1}{2}\) và \(b = 2.\) 2. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 3y = 4\\2x - 3y = - 1\end{array} \right.\) \(\left\{ \begin{array}{l}x + 3y = 4\\2x - 3y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 3\\x + 3y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\1 + 3y = 4\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\3y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right.\). Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {1;1} \right)\). Câu III (2,0 điểm) Cách giải: 1. Giải phương trình \({x^2} + 5x + 4 = 0\). Ta có: \(\begin{array}{l}\,\,\,\,\,\,{x^2} + 5x + 4 = 0\\ \Leftrightarrow {x^2} + x + 4x + 4 = 0\\ \Leftrightarrow \left( {{x^2} + x} \right) + \left( {4x + 4} \right) = 0\\ \Leftrightarrow x\left( {x + 1} \right) + 4\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x + 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 4\end{array} \right.\end{array}\) Vậy tập nghiệm của phương trình là \(S = \left\{ { - 1; - 4} \right\}\). 2. Cho phương trình \({x^2} + 5x + m - 2 = 0\) (\(m\) là tham số). Tìm các giá trị của \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,{x_2}\) thỏa mãn hệ thức \(\dfrac{1}{{{{\left( {{x_1} - 1} \right)}^2}}} + \dfrac{1}{{{{\left( {{x_2} - 1} \right)}^2}}} = 1\) Để phương trình đã cho có 2 nghiệm phân biệt \({x_1} \ne 1,\,\,{x_2} \ne 1\) thì \(\left\{ \begin{array}{l}\Delta > 0\\1 + 5 + m - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{5^2} - 4\left( {m - 2} \right) > 0\\m + 4 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}25 - 4m + 8 > 0\\m \ne - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4m < 33\\m \ne - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{{33}}{4}\\m \ne - 4\end{array} \right.\). Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 5\\{x_1}{x_2} = m - 2\end{array} \right.\). Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,\dfrac{1}{{{{\left( {{x_1} - 1} \right)}^2}}} + \dfrac{1}{{{{\left( {{x_2} - 1} \right)}^2}}} = 1 \Leftrightarrow \dfrac{{{{\left( {{x_1} - 1} \right)}^2} + {{\left( {{x_2} - 1} \right)}^2}}}{{{{\left( {{x_1} - 1} \right)}^2}.{{\left( {{x_2} - 1} \right)}^2}}} = 1\\ \Leftrightarrow x_1^2 - 2{x_1} + 1 + x_2^2 - 2{x_2} + 1 = {\left[ {{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1} \right]^2}\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) + 2 = {\left[ {{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1} \right]^2}\\ \Rightarrow 25 - 2\left( {m - 2} \right) - 2.\left( { - 5} \right) + 2 = {\left( {m - 2 + 5 + 1} \right)^2}\\ \Leftrightarrow 25 - 2m + 4 + 10 + 2 = {\left( {m + 4} \right)^2}\\ \Leftrightarrow - 2m + 41 = {m^2} + 8m + 16\\ \Leftrightarrow {m^2} + 10m - 25 = 0\,\,\left( * \right)\end{array}\) Ta có: \({\Delta _m} = {\left( { - 5} \right)^2} - \left( { - 25} \right) = 50 > 0\), do đó phương trình (*) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{m_1} = \dfrac{{ - 10 + \sqrt {50} }}{2} = - 5 + 5\sqrt 2 \\{m_1} = \dfrac{{ - 10 - \sqrt {50} }}{2} = - 5 - 5\sqrt 2 \end{array} \right.\,\,\left( {tm} \right)\). Vậy có hai giá trị của \(m\) thỏa mãn yêu cầu bài toán là \(m = - 5 \pm 5\sqrt 2 \). Câu IV (3,0 điểm) Cách giải: Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Các đường cao \(BD,\,\,CE\) (\(D\) thuộc \(AC\), \(E\) thuộc \(AB\)) của tam giác kéo dài lần lượt cắt đường tròn \(\left( O \right)\) tại các điểm \(M\) và \(N\) (\(M\) khác \(B\), \(N\) khác \(C\)).
1. Chứng minh tứ giác \(BCDE\) nội tiếp được trong một đường tròn. Vì \(BD,\,\,CE\) là các đường cao của \(\Delta ABC\) nên \(BD \bot AC,\,\,CE \bot AB\). \( \Rightarrow \angle BDC = \angle BEC = {90^0}\). Suy ra tứ giác \(BCDE\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau). 2. Chứng minh \(MN\) song song với \(DE\). Vì \(BCDE\) là tứ giác nội tiếp (cmt) nên \(\angle BDE = \angle BCE\) (hai góc nội tiếp cùng chắn cung \(BE\)). Mà \(\angle BCE = \angle BCN = \angle BMN\) (hai góc nội tiếp cùng chắn cung \(BN\) của \(\left( O \right)\)). \( \Rightarrow \angle BDE = \angle BMN\,\). Mà 2 góc này ở vị trí hai góc đồng vị bằng nhau. Vậy \(MN\parallel DE\,\,\,\left( {dhnb} \right)\,\,\left( {dpcm} \right)\). 3. Khi đường tròn \(\left( O \right)\) và dây \(BC\) cố định, điểm \(A\) di động trên cung lớn \(BC\) sao cho tam giác \(ABC\) nhọn, chứng minh bán kính đường tròn ngoại tiếp tam giác \(ADE\) không đổi và tìm vị trí của điểm \(A\) để diện tích tam giác \(ADE\) đạt giá trị lớn nhất. Gọi \(BD \cap CE = \left\{ H \right\}\). Xét tứ giác \(AEHD\) có \(\angle AEH + \angle ADH = {90^0} + {90^0} = {180^0}\). \( \Rightarrow AEHD\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)). Lại có \(\angle AEH = {90^0}\) nên là góc nội tiếp chắn nửa đường tròn, do đó tứ giác \(AEHD\) nội tiếp đường tròn đường kính \(AH\), tâm \(I\) là trung điểm của \(AH\). Suy ra đường tròn ngoại tiếp tam giác \(ADE\) là đường tròn \(\left( {I;\dfrac{{AH}}{2}} \right)\). Kẻ đường kính \(AF\) và gọi \(K\) là trung điểm của \(BC\). Vì \(\angle ABF,\,\,\angle ACF\) là các góc nội tiếp chắn nửa đường tròn \(\left( O \right)\) nên \(\angle ABF = \angle ACF = {90^0}\). Ta có: \(\left\{ \begin{array}{l}CF \bot AC\\BH \bot AC\,\,\left( {gt} \right)\end{array} \right. \Rightarrow CF\parallel BH\) (từ vuông góc đến song song). \(\left\{ \begin{array}{l}BF \bot AB\\CH \bot AB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow CH\parallel BF\) (từ vuông góc đến song song). \( \Rightarrow \) Tứ giác \(BHCF\) là hình bình hành (dhnb). \( \Rightarrow \) Hai đường chéo \(BC,\,\,HF\) cắt nhau tại trung điểm mỗi đường (tính chất hình bình hành). Mà \(K\) là trung điểm của \(BC\) (theo cách vẽ) nên \(K\) cũng là trung điểm của \(HF\). Khi đó \(OK\) là đường trung bình của tam giác \(AHF\) nên \(OK = \dfrac{1}{2}AH\) (tính chất đường trung bình). Suy ra đường tròn ngoại tiếp tam giác \(ADE\) là đường tròn \(\left( {I;OK} \right)\). Mà \(\left( O \right)\) và \(BC\) cố định, do đó \(O,\,\,K\) cố định nên \(OK\) không đổi. Vậy bán kính đường tròn ngoại tiếp tam giác \(ADE\) bằng \(OK\) không đổi. Ta có: \(\angle BAC = \dfrac{1}{2}\,\,sd\,\,cung\,\,BC\) (góc nội tiếp bằng nửa số đo cung bị chắn). Mà \(BC\) cố định nên \(sd\,\,cung\,\,BC\) không đổi. Do đó \(\angle BAC\) không đổi. Xét \(\Delta AED\) và \(\Delta ACB\) có: \(\angle BAC\) chung; \(\angle AED = \angle ACB\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp \(BCDE\)). \( \Rightarrow \Delta AED \sim \Delta ACB\,\,\left( {g.g} \right)\) theo tỉ số \(k = \dfrac{{AD}}{{AB}}\). Do đó ta có: \(\dfrac{{{S_{\Delta AED}}}}{{{S_{\Delta ACB}}}} = {k^2} = {\left( {\dfrac{{AD}}{{AB}}} \right)^2}\). Xét tam giác vuông \(ABD\) có: \(\dfrac{{AD}}{{AB}} = \cos \angle BAC\). \( \Rightarrow \dfrac{{{S_{\Delta AED}}}}{{{S_{\Delta ABC}}}} = {\cos ^2}\angle BAC\) \( \Rightarrow {S_{\Delta AED}} = {\cos ^2}\angle BAC.{S_{\Delta ABC}}\), mà \(\cos \angle BAC\) không đổi nên để \({S_{\Delta AED}}\) đạt giá trị lớn nhất thì \({S_{\Delta ABC}}\) phải lớn nhất. Kéo dài \(AH\) cắt \(BC\) tại \(P\) \( \Rightarrow AP \bot BC\) và \({S_{\Delta ABC}} = \dfrac{1}{2}AP.BC\). Do \(BC\) không đổi (theo giả thiết) nên \({S_{\Delta ABC}}\) đạt giá tị lớn nhất khi và chỉ khi \(AP\) lớn nhất. Khi đó \(A\) phải là điểm chính giữa của cung lớn \(BC\). Vậy \({S_{AED}}\) đạt giá trị lớn nhất khi \(A\) là điểm chính giữa của cung lớn \(BC\). Câu V (1,0 điểm) Cách giải: Cho ba số thực dương \(x,y,z\) thỏa mãn điều kiện \(x + y + z = xyz\). Tìm giá trị nhỏ nhất của biểu thức \(Q = \dfrac{{y + 2}}{{{x^2}}} + \dfrac{{z + 2}}{{{y^2}}} + \dfrac{{x + 2}}{{{z^2}}}\) Ta có: \(x + y + z = xyz \Rightarrow \dfrac{1}{{xy}} + \dfrac{1}{{yz}} + \dfrac{1}{{zx}} = 1\) Đặt \(\left\{ \begin{array}{l}a = \dfrac{1}{x}\\b = \dfrac{1}{y}\\c = \dfrac{1}{z}\end{array} \right.\left( {a,b,c > 0} \right)\) \( \Rightarrow ab + bc + ca = 1\). Khi đó \(\begin{array}{l}Q = {a^2}\left( {\dfrac{1}{b} + 2} \right) + {b^2}\left( {\dfrac{1}{c} + 2} \right) + {c^2}\left( {\dfrac{1}{a} + 2} \right)\\\,\,\,\, = \left( {\dfrac{{{a^2}}}{b} + \dfrac{{{b^2}}}{c} + \dfrac{{{c^2}}}{a}} \right) + 2\left( {{a^2} + {b^2} + {c^2}} \right)\end{array}\) Áp dụng BĐT \(\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} \ge \dfrac{{{{\left( {x + y} \right)}^2}}}{{a + b}}\) ta có: \(\dfrac{{{a^2}}}{b} + \dfrac{{{b^2}}}{c} + \dfrac{{{c^2}}}{a} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{b + c}} + \dfrac{{{c^2}}}{a} \ge \dfrac{{{{\left( {a + b + c} \right)}^2}}}{{a + b + c}} = a + b + c\) Lại có: \(\begin{array}{l}{a^2} + {b^2} \ge 2ab\\{b^2} + {c^2} \ge 2bc\\{c^2} + {a^2} \ge 2ca\\ \Rightarrow 2\left( {{a^2} + {b^2} + {c^2}} \right) \ge 2\left( {ab + bc + ca} \right)\\ \Rightarrow {a^2} + {b^2} + {c^2} \ge ab + bc + ca\end{array}\) \(\begin{array}{l}{\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca\\ \ge ab + bc + ca + 2ab + 2bc + 2ca\\ = 3\left( {ab + bc + ca} \right)\\ \Rightarrow a + b + c \ge \sqrt {3\left( {ab + bc + ca} \right)} = \sqrt 3 \end{array}\) Do đó \(\begin{array}{l}\left( {\dfrac{{{a^2}}}{b} + \dfrac{{{b^2}}}{c} + \dfrac{{{c^2}}}{a}} \right) + 2\left( {{a^2} + {b^2} + {c^2}} \right)\\ \ge a + b + c + 2\left( {ab + bc + ca} \right)\\ \ge \sqrt 3 + 2\end{array}\) Vậy \({Q_{\min }} = \sqrt 3 + 2\). Dấu “=” xảy ra khi \(a = b = c = \dfrac{1}{{\sqrt 3 }} \Rightarrow x = y = z = \sqrt 3 \).
|




















Danh sách bình luận