Đề thi vào 10 môn Toán Bắc Ninh năm 2021

Đề bài

I. PHẦN TRẮC NGHIỆM (4,0 điểm)

Câu 1. Cho tam giác \(ABC\) vuông tại \(A,AB = 3\,\,cm,AC = 4\,\,cm\) thì \(\tan C\) bằng:

     A. \(\dfrac{4}{3}\)             B. \(\dfrac{5}{3}\)                  C. \(\dfrac{3}{5}\)                  D.\(\dfrac{3}{4}\)    

Câu 2. Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(BH = 4\,\,cm,CH = 9\,\,cm\). Độ dài đoạn thẳng \(AH\) bằng:

     A. \(36\,\,cm\)                    B. \(\sqrt {13} \,\,cm\)            C. \(6\,\,cm\)                           D. \(9\,\,cm\)     

Câu 3. Nghiệm \(\left( {x;y} \right)\) của hệ phương trình \(\left\{ \begin{array}{l}3x + 3y = 3\\x - 3y = 5\end{array} \right.\) là:

     A. \(\left( { - 2; - 1} \right)\)                                             B. \(\left( {2; - 1} \right)\)      C. \(\left( { - 2;1} \right)\)                                   D. \(\left( { - 1;2} \right)\)    

Câu 4. Biểu thức \(\sqrt {16{x^2}{y^4}} \) bằng:

     A. \( - 4x{y^2}\)                B. \(4{x^2}{y^4}\)                  C. \(4x{y^2}\)                         D. \(4\left| x \right|{y^2}\)                         

Câu 5. Tất cả các giá trị của \(x\) để biểu thức \(\sqrt {x - 3} \) có nghĩa là:

     A. \(x \ge 3\)                      B. \(x < 3\)                              C. \(x \le 3\)                            D. \(x > 3\) 

Câu 6. Cho tứ giác \(ABCD\) nội tiếp đường tròn tâm \(O\). Biết \(\angle DBC = {55^0}\). Số đo \(\angle DAC\) bằng:

     A. \({35^0}\)                      B. \({55^0}\)                           C. \({65^0}\)                           D. \({30^0}\)     

Câu 7. Cho parabol \(\left( P \right):y = 2{x^2}\) và đường thẳng \(d:y = 2x - 1\), số giao điểm của \(d\) và \(\left( P \right)\) là:

     A. \(3\)                               B. \(2\)                                    C. \(0\)                                    D. \(1\)       

Câu 8. Khi \(x = 3\), biểu thức \(M = \sqrt[3]{{{x^2} - 1}}\) có giá trị bằng:

     A. \(\sqrt 8 \)                     B. \(4\)                                    C. \(2\)                                    D. \(8\)       

Câu 9. Đường thẳng \(d:y = mx + 2\) đi qua điểm \(A\left( {1;1} \right)\) khi giá trị của \(m\) bằng:

     A. \( - 3\)                            B. \( - 1\)                                 C. \( - 2\)                                D. \(1\)       

Câu 10. Đồ thị hàm số \(y = a{x^2}\) với \(a\) là số thức dương có hình dạng nào dưới đây?

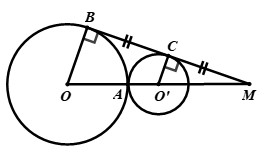
     A. Hình 3.                          B. Hình 2.                               C. Hình 4.                              D. Hình 1. 

Câu 11. Tất cả các giá trị của \(m\) để hàm số \(y = \left( {m + 2} \right)x + m\left( {m \ne  - 2} \right)\) đồng biến trên \(\mathbb{R}\) là:

     A. \(m >  - 2\)                    B. \(m <  - 2\)                         C. \(m > 0\)                            D. \(m > 2\)      

Câu 12. Tổng hai nghiệm của phương trình \({x^2} - x - 6 = 0\) bằng:

     A. \( - 6\)                            B. \(6\)                                    C. \( - 1\)                                D. \(1\)       

Câu 13. Hàm số \(y =  - 100{x^2}\) đồng biến khi:

     A. \(x \ne 0\)                      B. \(x < 0\)                              C. \(x > 0\)                              D. \(x > 0\) 

Câu 14. Hệ phương trình  có nghiệm duy nhất khi

     A. \(m \ne 1\)                     B. \(m = 1\)                            C. \(m \ne 0\)                         D. \(m \ne  - 1\)

Câu 15. Tất cả các giá trị của \(m\) để phương trình \({x^2} - 2mx + 1 = 0\) có nghiệm kép là:

     A. \(m =  - 2\)                    B. \(m > 1\)                            C. \(m =  \pm 1\)                   D. \(m = 4\)      

Câu 16. Hệ phương trình \(\left\{ \begin{array}{l}ax + y = 3\\x + by = 1\end{array} \right.\) có nghiệm \(\left( {x;y} \right) = \left( {2; - 1} \right)\). Giá trị của \(a + b\) bằng:

     A. \(4\)                               B. \( - 3\)                                 C. \( - 1\)                                D. \(3\)       

Câu 17. Tam giác vuông cân có độ dài cạnh góc vuông bằng \(2\,\,cm\). Bán kính đường tròn ngoại tiếp tam giác đó bằng:

     A. \(\sqrt 2 \,\,cm\)            B. \(2\sqrt 2 \,\,cm\)               C. \(2\,\,cm\)                           D. \(\sqrt 3 \,\,cm\)    

Câu 18. Tất cả các giá trị của \(m\) để phương trình \({x^2} - \left( {m + 1} \right)x + m = 0\) có hai nghiệm phân biệt và nghiệm này gấp hai lần nghiệm kia là:

     A. \(m = 2\)                       B. \(m = 2;m = \dfrac{1}{2}\)                                              C. \(m = 0\)       D. \(m = \dfrac{1}{2}\)              

Câu 19. Biết \(m,n\) là các số nguyên sao cho phương trình \(m{x^2} + nx - 5 - 3\sqrt 3  = 0\) có nghiệm \(x = \sqrt 3  + 1\). Khẳng định nào dưới đây đúng?

     A. \(m + n = 2\sqrt 3 \)     B. \(m + n = 2\)                      C. \(m + n = 0\)                      D. \(m + n = \dfrac{5}{3}\)                        

Câu 20. Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';r} \right)\) tiếp xúc ngoài với nhau tại điểm \(A\) biết \(R > r > 0\). Tiếp tuyến chung ngoài \(BC\) của hai đường tròn đó cắt đường nối tâm \(OO'\) tại \(M\), trong đó \(B \in \left( O \right),C \in \left( {O'} \right)\) và \(BC = CM = 4\,\,cm\). Tổng \(R + r\) bằng:

     A. \(3\sqrt 2 \,\,cm\)          B. \(5\sqrt 2 \,\,cm\)               C. \(4\,\,cm\)                           D. \(6\,\,cm\)     

II. TỰ LUẬN (6,0 điểm)

Câu 1 (2,0 điểm):

a) Giải phương trình: \({x^2} - 4x - 5 = 0\)

b) Rút gọn biểu thức \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x  - 2}} + \dfrac{1}{{\sqrt x  + 2}}\,\,\,\,\left( {x \ge 0;x \ne 4} \right)\)

Câu 2 (1,5 điểm):

Một người đi siêu thị điện máy mua một chiếc quạt điện và một chiếc đèn tích điện, biết tổng số tiền theo giá niêm yết của hai sản phẩm là \(900000\) đồng. Nhưng do siêu thị đang có chương trình giảm giá, quạt điện được giảm giá \(15\% \), đèn tích điện được giảm giá \(10\% \) nên thực tế người đó chỉ phải thanh toán tổng số tiền cho hai sản phẩm là \(780000\) đồng. Hỏi giá niêm yết của mỗi sản phẩm nêu trên là bao nhiêu tiền?

Câu 3 (2,0 điểm):

Cho đường tròn tâm \(O\) đường kính \(AB\) và dây \(AB\) vuông góc với \(AB\) tại điểm \(F\). Trên cung nhỏ \(BC\) lấy điểm \(M\) (\(M\) không trùng với \(B\) và \(C\)), đường thẳng \(AM\) cắt đường thẳng \(CD\) tại \(E\).

a) Chứng minh tứ giác EFBM nội tiếp được trong một đường tròn và \(\angle CMA = \angle DMA\)

b) Gọi giao điểm của hai đường thẳng \(AC\) và \(BM\) là \(K\); giao điểm của hai đường thẳng \(DM\) và \(AB\) là \(I\); giao điểm của hai đường thẳng \(AM\) và \(BC\) là \(N\). Chứng minh ba điểm \(K,N,I\) thẳng hàng.

Câu 4 (0,5 điểm)

Cho \(a,b,c\) là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{3\left( {b + c} \right)}}{{2a}} + \dfrac{{4a + 3c}}{{3b}} + \dfrac{{12\left( {b - c} \right)}}{{2a + 3c}}.\)

Lời giải chi tiết

I. PHẦN TRẮC NGHIỆM

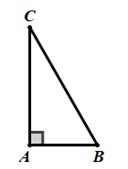
Câu 1

Phương pháp:

Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.

Cách giải:

 Tam giác \(ABC\) vuông tại \(A\), ta có:

\(\tan C = \dfrac{{AB}}{{AC}} = \dfrac{3}{4}\) (tỉ số lượng giác của góc nhọn trong tam giác vuông)

Chọn D.

Câu 2

Phương pháp:

Áp dụng hệ thức lượng trong tam giác vuông.

Cách giải:

Tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) nên ta có:

\(A{H^2} = BH.HC\) (hệ thức lượng trong tam giác vuông)

\(\begin{array}{l} \Rightarrow A{H^2} = 4.9 = 36\\ \Rightarrow AH = 6\,\,\left( {cm} \right)\end{array}\)

Chọn C.

Câu 3

Phương pháp:

Sử dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình.

Cách giải:

\(\left\{ \begin{array}{l}3x + 3y = 3\\x - 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x = 8\\x - 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2 - 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y =  - 1\end{array} \right.\)

Vậy nghiệm của hệ phương trình \(\left( {x;y} \right) = \left( {2; - 1} \right)\)

Chọn B.

Câu 4

Phương pháp:

Sử dụng hằng đẳng thức: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)

Cách giải:

Ta có: \(\sqrt {16{x^2}{y^4}}  = \sqrt {{{\left( {4x{y^2}} \right)}^2}}  = 4\left| x \right|{y^2}\)

Chọn D.

Câu 5

Phương pháp:

\(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0\)

Cách giải:

Biểu thức \(\sqrt {x - 3} \) có nghĩa \( \Leftrightarrow x - 3 \ge 0 \Leftrightarrow x \ge 3\)

Chọn A.

Câu 6

Phương pháp:

Các góc nội tiếp cùng chắn một cung thì có số đo bằng nhau.

Cách giải:

Tứ giác \(ABCD\) nội tiếp\( \Rightarrow \angle DBC = \angle DAC\) (góc nội tiếp cùng chắn cung \(CD\))

Mà \(\angle DBC = {55^0} \Rightarrow \angle DAC = {55^0}\)

Chọn B.

Câu 7

Phương pháp:

Xét phương trình hoành độ giao điểm của \(d\) và \(\left( P \right)\) , giải phương trình hoành độ giao điểm và tìm được giao điểm.

Cách giải:

Phương trình hoành độ giao điểm của \(d\) và \(\left( P \right)\) là:

\(\begin{array}{l}\,\,\,\,\,\,\,\,2{x^2} = 2x - 1\\ \Leftrightarrow 2{x^2} - 2x + 1 = 0\end{array}\)

Xét \(\Delta ' = {\left( { - 1} \right)^2} - 1.2 = 1 - 2 =  - 1 < 0\)

\( \Rightarrow \) Phương trình vô nghiệm

\( \Rightarrow \) \(d\) và \(\left( P \right)\) không cắt nhau nên không có giao điểm, nên số giao điểm là \(0\).

Chọn C.

Câu 8

Phương pháp:

Thay \(x = 3\), ta tính được giá trị của biểu thức \(M\).

Cách giải:

Thay \(x = 3\) vào biểu thức \(M = \sqrt[3]{{{x^2} - 1}}\), ta được: \(M = \sqrt[3]{{{3^2} - 1}} = \sqrt[3]{8} = 2\)

Chọn C.

Câu 9

Phương pháp:

Đường thẳng \(\left( d \right):y = ax + b\) đi qua điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) khi \({y_A} = a{x_A} + b\).

Cách giải:

Đường thẳng \(d:y = mx + 2\) đi qua điểm \(A\left( {1;1} \right)\) nên ta có: \(1 = m + 2 \Rightarrow m =  - 1\)

Chọn B.

Câu 10

Phương pháp:

Nhận dạng dáng điệu của đồ thị hàm số dựa vào hàm số.

Cách giải:

Hai đồ thị hình 3 và hình 4 không phải là đồ thị của hàm số \(y = a{x^2}\)\( \Rightarrow \) loại đáp án A và C.

Hàm số \(y = a{x^2}\) với \(a\) là số thức dương nên hàm số hoàn toàn phía trên trục hoành \( \Rightarrow \) loại đáp án B.

Chọn D.

Câu 11

Phương pháp:

Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\)

Cách giải:

Hàm số \(y = \left( {m + 2} \right)x + m\left( {m \ne  - 2} \right)\) đồng biến trên \(\mathbb{R}\)\( \Leftrightarrow m + 2 > 0 \Leftrightarrow m >  - 2\)

Chọn A.

Câu 12

Phương pháp:

Nếu phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) khi đó, áp dụng hệ thức Vi – ét, ta có: \({x_1} + {x_2} = \dfrac{{ - b}}{a}\)

Cách giải:

Ta có: \(\Delta  = {\left( { - 1} \right)^2} - \left( { - 6} \right) = 7 > 0\)

\( \Rightarrow \) Phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) khi đó, áp dụng hệ thức Vi – ét, ta có: \({x_1} + {x_2} = \dfrac{{ - b}}{a} = \dfrac{1}{1} = 1\)

Chọn D.

Câu 13

Phương pháp:

Hàm số \(y = a{x^2}\,\,\left( {a < 0} \right)\) đồng biến khi \(x < 0\)

Cách giải:

Hàm số \(y =  - 100{x^2}\)  có \(a =  - 100 < 0\) nên hàm số đồng biến khi \(x < 0\)

Chọn B.

Câu 14

Phương pháp:

Hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) có nghiệm duy nhất khi và chỉ khi \(\dfrac{a}{{a'}} \ne \dfrac{b}{{b'}}\)

Cách giải:

Hệ phương trình \(\left\{ \begin{array}{l}mx + y = 1\\x + y = 5\end{array} \right.\) có nghiệm duy nhất khi \(\dfrac{m}{1} \ne \dfrac{1}{1} \Rightarrow m \ne 1\)

Chọn A.

Câu 15

Phương pháp:

Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm kép \( \Leftrightarrow \Delta  = 0\) (hoặc \(\Delta ' = 0\))

Cách giải:

Ta có: \(\Delta ' = {\left( { - m} \right)^2} - 1 = {m^2} - 1\)

Phương trình có nghiệm kép \( \Leftrightarrow \Delta ' = 0\)

          \(\begin{array}{l} \Leftrightarrow {m^2} - 1 = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m =  - 1\end{array} \right.\end{array}\)

Vậy \(m = 1\) hoặc \(m =  - 1\).

Chọn C.

Câu 16

Phương pháp:

Thay \(x = 2;y =  - 1\) vào hệ phương trình của đề bài, tìm được \(a;b\).

Cách giải:

Thay \(x = 2;y =  - 1\) vào hệ phương trình \(\left\{ \begin{array}{l}ax + y = 3\\x + by = 1\end{array} \right.\), ta được: \(\left\{ \begin{array}{l}a.2 + \left( { - 1} \right) = 3\\2 + b.\left( { - 1} \right) = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 1\end{array} \right.\)

Khi đó, \(a + b = 3\)

Chọn D.

Câu 17

Phương pháp:

Bán kính đường tròn ngoại tiếp tam giác vuông bằng một nửa cạnh huyền.

Cách giải:

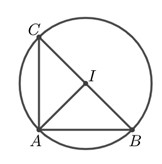
Giả sử tam giác \(ABC\) vuông cân tại \(A\) có \(AB = AC = 2cm\)

Gọi \(I\) là trung điểm của \(BC\), khi đó \(IA = IB = IC\)

\( \Rightarrow \) \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).

\( \Rightarrow \) Bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = IA\)

Tam giác \(ABC\) vuông cân tại \(A \Rightarrow BC = 2\sqrt 2 \left( {cm} \right) \Rightarrow IA = \sqrt 2 \left( {cm} \right)\)

Vậy bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(\sqrt 2 cm\).

Chọn A.

Câu 18

Phương pháp:

Phương trình có hai nghiệm phân biệt \({x_1};{x_2}\) \( \Leftrightarrow \Delta  > 0\)

Áp dụng hệ thức Vi – ét, tìm được giá trị của \(m\).

Cách giải:

Phương trình có hai nghiệm phân biệt \({x_1};{x_2}\) \( \Leftrightarrow \Delta  > 0\)

\(\begin{array}{l} \Leftrightarrow {\left( {m + 1} \right)^2} - 4m > 0\\ \Leftrightarrow {m^2} + 2m + 1 - 4m > 0\\ \Leftrightarrow {m^2} - 2m + 1 > 0\\ \Leftrightarrow {\left( {m - 1} \right)^2} > 0\\ \Leftrightarrow m \ne 1\end{array}\)

Vậy \(m \ne 1\) phương trình có hai nghiệm phân biệt \({x_1};{x_2}\)

Áp dụng hệ thức Vi – ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 1\,\,\,\,\left( 1 \right)\\{x_1}{x_2} = m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Giả sử \({x_1} = 2{x_2}\), thay vào (1), ta có: \(2{x_2} + {x_2} = m + 1\)

\(\begin{array}{l} \Leftrightarrow 3{x_2} = m + 1\\ \Leftrightarrow {x_2} = \dfrac{{m + 1}}{3} \Rightarrow {x_1} = \dfrac{{2\left( {m + 1} \right)}}{3}\end{array}\)

Thay vào (2), ta được: \(\dfrac{{\left( {m + 1} \right)}}{3}.\dfrac{{2\left( {m + 1} \right)}}{3} = m\)

\(\begin{array}{l} \Rightarrow 2{\left( {m + 1} \right)^2} = 9m\\ \Leftrightarrow 2\left( {{m^2} + 2m + 1} \right) = 9m\\ \Leftrightarrow 2{m^2} + 4m + 2 = 9m\end{array}\)

\(\begin{array}{l} \Leftrightarrow 2{m^2} - 5m + 2 = 0\\ \Leftrightarrow \left( {2m - 1} \right)\left( {m - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2m - 1 = 0\\m - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{1}{2}\left( {tmdk} \right)\\m = 2\left( {tmdk} \right)\end{array} \right.\end{array}\)

Vậy \(m = \dfrac{1}{2};m = 2\).

Chọn B.

Câu 19

Phương pháp:

Thay \(x = \sqrt 3  + 1\) vào phương trình.

Dựa vào đáp án của đề bài tìm được \(m,n\).

Cách giải:

Vì \(m,n\) là các số nguyên nên loại đáp án A và D.

Phương trình \(m{x^2} + nx - 5 - 3\sqrt 3  = 0\) có nghiệm \(x = \sqrt 3  + 1\), nên ta có:

\(m{\left( {\sqrt 3  + 1} \right)^2} + n\left( {\sqrt 3  + 1} \right) - 5 - 3\sqrt 3  = 0\)\(\left( * \right)\)

TH1: \(m + n = 2 \Rightarrow n = 2 - m\)

Thay vào phương trình \(\left( * \right)\), ta được:

\(\begin{array}{l}\,\,\,\,\,\,\,\,m\left( {3 + 2\sqrt 3  + 1} \right) + \left( {2 - m} \right)\left( {\sqrt 3  + 1} \right) - 5 - 3\sqrt 3  = 0\\ \Leftrightarrow \left( {3 + 2\sqrt 3  + 1 - \sqrt 3  - 1} \right)m + 2\sqrt 3  + 2 - 5 - 3\sqrt 3  = 0\\ \Leftrightarrow \left( {3 + \sqrt 3 } \right)m - \sqrt 3  - 3 = 0\\ \Leftrightarrow \left( {3 + \sqrt 3 } \right)m = \sqrt 3  + 3\\ \Leftrightarrow m = 1\left( {tm} \right)\\ \Rightarrow n = 2 - 1 = 1\left( {tm} \right)\end{array}\)

Vậy \(m + n = 2\) thỏa mãn.

Chọn B.

Câu 20

Phương pháp:

Vận dụng dấu hiệu nhận biết và tính chất của đường trung bình trong tam giác

Phát hiện mối quan hệ giữa \(R\) và \(r\), từ đó biểu diễn \(r\) theo \(R\)

Áp dụng định lý Py – ta – go, tính được \(R\) và \(r\).

Cách giải:

Ta có: \(B,C,M\) thẳng hàng mà \(BC = CM = 4cm\)

\( \Rightarrow C\)là trung điểm của \(BM\)

\(BC\) là tiếp tuyến chung của đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) nên

\(OB//O'C\)

\(\Delta OBM\) có: \(C\) là trung điểm của \(BM\)

\(OB//O'C\)

\( \Rightarrow O'C\) là đường trung bình của \(\Delta OBM\) (dhnb đường trung bình trong tam giác)

\( \Rightarrow O'C = \dfrac{1}{2}OB\) hay \(r = \dfrac{1}{2}R\)

   Và  \(O'\) là trung điểm của \(OM\)\( \Rightarrow OM = 2OO'\)

Vì \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài với nhau tại \(A\) nên \(OO' = OA + AO' = R + r\)

Do đó \(OM = 2\left( {R + r} \right) = 2\left( {R + \dfrac{1}{2}R} \right) = 2.\dfrac{3}{2}R = 3R\)

\(\Delta OBM\) vuông tại \(B\), theo định lý Py – ta – go, ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,O{B^2} + B{M^2} = O{M^2}\\ \Leftrightarrow {R^2} + {8^2} = {\left( {3R} \right)^2}\\ \Leftrightarrow 9{R^2} - {R^2} = 64\\ \Leftrightarrow 8{R^2} = 64\\ \Leftrightarrow {R^2} = 8\\ \Rightarrow R = 2\sqrt 2 \left( {cm} \right)\end{array}\)

Khi đó, \(r = \dfrac{1}{2}R = \dfrac{1}{2}.2\sqrt 2  = \sqrt 2 \left( {cm} \right)\)

Vậy \(R + r = 2\sqrt 2  + \sqrt 2  = 3\sqrt 2 \left( {cm} \right)\)

Chọn A.

II. PHẦN TỰ LUẬN:

Câu 1

Phương pháp:

a) Cách 1: Đưa phương trình về dạng \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)    

Cách 2: Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a - b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = 1;{x_2} = \dfrac{{ - c}}{a}\)

b) Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a  - \sqrt b } \right)\left( {\sqrt a  + \sqrt b } \right)\) xác định mẫu thức chung của biểu thức

Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.

Cách giải:

a) \({x^2} - 4x - 5 = 0\)

Cách 1:

\(\begin{array}{l}\,\,\,\,\,\,\,\,{x^2} - 4x - 5 = 0\\ \Leftrightarrow {x^2} - 5x + x - 5 = 0\\ \Leftrightarrow x\left( {x - 5} \right) + \left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\x =  - 1\end{array} \right.\end{array}\)

Vậy phương trình có tập nghiệm là \(S = \left\{ { - 1;5} \right\}\)

Cách 2: \({x^2} - 4x - 5 = 0\)

Phương trình có: \(a - b + c = 1 + 4 - 5 = 0\)

\( \Rightarrow \) Phương trình có nghiệm \({x_1} =  - 1\) và \({x_2} =  - \dfrac{c}{a} = 5.\)

Vậy phương trình có tập nghiệm là \(S = \left\{ { - 1;5} \right\}\)

b) Điều kiện: \(x \ge 0,\,\,x \ne 4.\)

\(\begin{array}{l}A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x  - 2}} + \dfrac{1}{{\sqrt x  + 2}}\,\,\,\\\,\,\,\,\, = \dfrac{x}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} + \dfrac{1}{{\sqrt x  - 2}} + \dfrac{1}{{\sqrt x  + 2}}\\\,\,\,\,\, = \dfrac{{x + \sqrt x  + 2 + \sqrt x  - 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\\,\,\,\, = \dfrac{{x + 2\sqrt x }}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\\,\,\,\, = \dfrac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\\,\,\, = \dfrac{{\sqrt x }}{{\sqrt x  - 2}}.\end{array}\)

Vậy \(A = \dfrac{{\sqrt x }}{{\sqrt x  - 2}}\) khi \(x \ge 0,\,\,x \ne 4.\)

Câu 2

Phương pháp:

Gọi giá niêm yết của quạt điện là \(x\,\)(đồng) \(\left( {x \in \mathbb{N}*,\,x < 900000} \right)\)

Giá niêm yết của chiếc đèn tích điện là \(y\) (đồng) \(\left( {y \in \mathbb{N}*,\,y < 900000} \right)\)

Tính được giá của quạt điện và đèn tích điện sau khi giảm.

Lập được hệ phương trình, giải hệ phương trình, đối chiếu điều kiện và kết luận.

Cách giải:

Gọi giá niêm yết của quạt điện là \(x\,\)(đồng) \(\left( {x \in \mathbb{N}*,\,x < 900000} \right)\)

Giá niêm yết của chiếc đèn tích điện là \(y\) (đồng) \(\left( {y \in \mathbb{N}*,\,y < 900000} \right)\)

\( \Rightarrow \) Giá của quạt điện sau khi giảm \(15\% \) là \(x - 0,15x = 0,85x\) (đồng)

Giá của chiếc đèn tích điện sau khi giảm \(10\% \) là \(y - 0,1y = 0,9y\) (đồng)

Do tổng số tiền theo giá niêm yết của hai sản phẩm là \(900000\) đồng và tổng số tiền sau khi đã giảm giá của   đồng nên ta có hệ phương trình:

\(\begin{array}{l}\,\,\,\,\,\,\left\{ \begin{array}{l}x + y = 900000\\0,85x + 0,9y = 780000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 900000 - x\\0,85x + 0,9.\left( {900000 - x} \right) = 780000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 900000 - x\\0,85x + 810000 - 0,9x = 780000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0,05x = 30000\\y = 900000 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 600000\\y = 300000\end{array} \right.\,\,\,\left( {tm} \right)\end{array}\)

Vậy giá niêm yết của quạt điện là \(600000\) đồng và giá niêm yết của chiếc đèn tích điện là \(300000\) đồng.

Câu 3 (VD):

Phương pháp:

a) + Vận dụng dấu hiệu nhận biết: tứ giác có tổng hai góc đối nhau bằng \({180^0}\) là tứ giác nội tiếp.

+ Sử dụng kiến thức góc nội tiếp cùng chắn cung trong đường tròn.

b) Ta sẽ chứng minh: \(KN \bot AB\) và \(NI \bot AB\) tại \(I\), từ đó suy ra \(K,N,I\) thẳng hàng.

Cách giải:

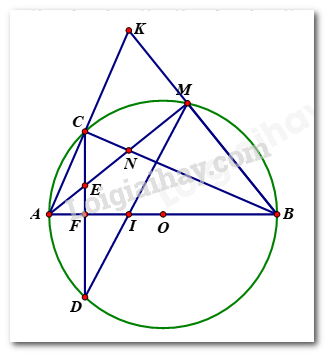
a) Chứng minh tứ giác EFBM nội tiếp được trong một đường tròn và \(\angle CMA = \angle DMA\)

Vì \(M \in \left( O \right)\); \(AB\) là đường kính của \(\left( O \right)\)

\( \Rightarrow \angle AMB = {90^0}\)

Ta có: \(CD \bot AB\) tại \(F\) (gt), \(E \in CD\)\( \Rightarrow \angle EFB = {90^0}\)

Xét tứ giác \(EFBM\), có:

\(\begin{array}{l}\angle AMB = {90^0}\\\angle EFB = {90^0}\end{array}\)

Mà hai góc này ở vị trí đối nhau

\( \Rightarrow \) Tứ giác \(EFBM\) nội tiếp một đường tròn (đpcm)

Vì \(CD \bot AB\) tại \(F\) (gt) \( \Rightarrow F\) là trung điểm của \(CD\) (định lí về mối liên hệ giữa đường kính và dây cung)

Xét \(\Delta ACD\) có:

            \(F\) là trung điểm của \(CD\) (cmt)

            \(AF \bot CD\) (do \(AB \bot CD\), \(F \in AB)\))

\( \Rightarrow AF\) là đường cao đồng thời là đường trung trực của \(\Delta ACD\)

\( \Rightarrow \Delta ACD\) cân tại \(A\)

\( \Rightarrow \angle ACD = \angle ADC\) (tính chất)

Mà \(\angle ADC = \angle CMA\) (2 góc nội tiếp cùng chắn cung \(AC\))

      \(\angle AMD = \angle ACD\) (2 góc nội tiếp cùng chắn cung \(AD\))

Do đó: \(\angle AMD = \angle CMA\) (đpcm)

b) Gọi giao điểm của hai đường thẳng \(AC\) và \(BM\) là \(K\); giao điểm của hai đường thẳng \(DM\) và \(AB\) là \(I\); giao điểm của hai đường thẳng \(AM\) và \(BC\) là \(N\). Chứng minh ba điểm \(K,N,I\) thẳng hàng.

Ta có: \(\angle ACB = {90^o}\) ( góc nội tiếp chắn nửa đường tròn) \( \Rightarrow CB \bot AC\) hay \(CB \bot AK\,\)

           \(\angle AMB = {90^o}\)( góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AM \bot MB\) hay \(AM \bot BK\)

Xét \(\Delta AKB\) có:

            \(\begin{array}{l}CB \bot AK\\AM \bot KB\end{array}\)

Mà \(CB \cap AN = \left\{ N \right\}\)

\( \Rightarrow N\) là trực tâm của \(\Delta AKB\)

\( \Rightarrow KN\) là đường cao thứ ba của \(\Delta AKB\)

\( \Rightarrow KN \bot AB\,\,\left( 1 \right)\)

Ta có: \(\angle NMI = \angle IBN\) (cùng bù với góc \(\angle ADC\))

Xét tứ giác \(NMBI\) có: \(\angle NMI = \angle IBN\) (cmt)

Mà hai góc này cùng nhìn cạnh \(IN\) dưới một góc không đổi.

\( \Rightarrow \)Tứ giác \(NMBI\) nội tiếp một đường tròn

\( \Rightarrow \angle NMB + \angle NIB = {180^0}\) (2 góc đối nhau)

\(\begin{array}{l} \Rightarrow {90^0} + \angle NIB = {180^0}\\ \Rightarrow \angle NIB = {90^0}\end{array}\)

\( \Rightarrow NI \bot IB\) tại \(I\) hay \(NI \bot AB\) tại \(I\) \(\left( 2 \right)\)

\(\left( 1 \right),\left( 2 \right) \Rightarrow K,N,I\) thằng hàng (đpcm).

Câu 4

Phương pháp:

Tách nhóm hợp lí, đưa về giả thiết của bài toán.

Cách giải

Ta có:

\(\begin{array}{l}P = \dfrac{{3\left( {b + c} \right)}}{{2a}} + \dfrac{{4a + 3c}}{{3b}} + \dfrac{{12\left( {b - c} \right)}}{{2a + 3c}}\\ = \left[ {\dfrac{{3\left( {b + c} \right)}}{{2a}} + 2} \right] + \left[ {\dfrac{{4a + 3c}}{{3b}} + 1} \right] + \left[ {\dfrac{{12\left( {b - c} \right)}}{{2a + 3c}} + 8} \right] - 11\\ = \dfrac{{4a + 3b + 3c}}{{2a}} + \dfrac{{4a + 3b + 3c}}{{3b}} + \dfrac{{4\left( {4a + 3b + 3c} \right)}}{{2a + 3c}} - 11\\ = \left( {4a + 3b + 3c} \right)\left( {\dfrac{1}{{2a}} + \dfrac{1}{{3b}} + \dfrac{4}{{2a + 3c}}} \right) - 11\\ = \left[ {2a + 3b + \left( {2a + 3c} \right)} \right]\left( {\dfrac{1}{{2a}} + \dfrac{1}{{3b}} + \dfrac{4}{{2a + 3c}}} \right) - 11\\ \ge {\left( {1 + 1 + 2} \right)^2} - 11 = 5\end{array}\)

Dấu bằng xảy ra \( \Leftrightarrow 2a = 3b = \dfrac{{2a + 3c}}{2}\)

\( \Leftrightarrow \left\{ \begin{array}{l}2a = 3b\\4a = 2a + 3c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a = 3b\\2a = 3c\end{array} \right. \Leftrightarrow 2a = 3b = 3c\)

Vậy giá trị nhỏ nhất của \(P = 5\) khi \(2a = 3b = 3c\).