Đề thi vào 10 môn Toán Quảng Ngãi năm 2019Tải vềBài 1 (1,0 điểm): a) Cho biểu thức Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
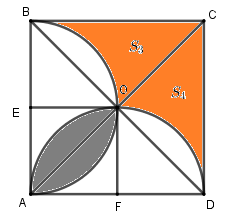
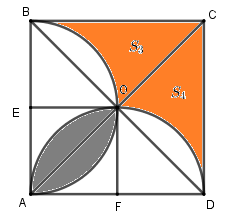
Đề bài Bài 1 (1,0 điểm): a) Cho biểu thức \(A = \sqrt {16} - \sqrt {25} + \sqrt 4 \). So sánh \(A\) với \(\sqrt 2 \). b) Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = - 5\\2x + y = 11\end{array} \right.\). Bài 2 (2,5 điểm): 1. Cho parabol \(\left( P \right):y = - {x^2}\) và đường thẳng \(\left( d \right):y = x - 2\) a) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\) b) Viết phương trình đường thẳng \(\left( {d'} \right)\) song song với \(\left( d \right)\) và tiếp xúc với \(\left( P \right).\) 2. Cho phương trình \({x^2} - 4x + m = 0\) (\(m\) là tham số) a) Biết phương trình có một nghiệm bằng \( - 1.\) Tính nghiệm còn lại. b) Xác định \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(\left( {3{x_1} + 1} \right)\left( {3{x_2} + 1} \right) = 4\) Bài 3 (2,0 điểm): Một đội công nhân đặt kế hoạch sản xuất 250 sản phẩm. Trong 4 ngày đầu, họ thực hiện đúng kế hoạch. Mỗi ngày sau đó, họ đều làm vượt mức 5 sản phẩm nên đã hoàn thành công việc sớm hơn 1 ngày. Hỏi theo kế hoạch, mỗi ngày đội công nhân đó làm được bao nhiêu sản phẩm? Biết rằng năng suất làm việc của mỗi công nhân là như nhau? Bài 4 (3,5 điểm): Cho tam giác nhọn \(\Delta ABC\,\,\left( {AB < AC} \right),\) đường cao \(AH\), nội tiếp đường tròn \(\left( O \right).\) Gọi \(D\) và \(E\) thứ tự là hình chiếu vuông góc của \(H\) lên \(AB\) và \(AC.\) a) Chứng minh các tứ giác \(AEHD\) và \(BDEC\) nội tiếp được đường tròn. b) Vẽ đường kính \(AF\) của đường tròn \(\left( O \right).\) Chứng minh \(BC = \sqrt {AB.BD} + \sqrt {AC.CE} \) và \(AF \bot DE.\) c) Gọi \(O'\) là tâm đường tròn ngoại tiếp \(\Delta BDE.\) Chứng minh \(O'\) là trung điểm của đoạn thẳng \(HF.\) d) Tính bán kính của đường tròn \(\left( {O'} \right)\) biết \(BC = 8cm,\,\,DE = 6cm,\,\,AF = 10cm.\) Bài 5 (1 điểm): Cho hình vuông \(ABCD\). Gọi \({S_1}\) là diện tích phần giao của hai nửa đường tròn đường kính AB và CD ; \({S_2}\) là diện tích phần còn lại của hình vuông ABCD nằm ngoài hai nửa hình tròn nói trên (như hình vẽ bên). Tính tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\).
Lời giải chi tiết Bài 1: Phương pháp: a) Rút gọn \(A\), sử dụng hẳng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\). b) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số. Cách giải: a) Cho biểu thức \(A = \sqrt {16} - \sqrt {25} + \sqrt 4 \). So sánh \(A\) với \(\sqrt 2 \). \(A = \sqrt {16} - \sqrt {25} + \sqrt 4 = \sqrt {{4^2}} - \sqrt {{5^2}} + \sqrt {{2^2}} = 4 - 5 + 2 = 1\) Ta có: \(1 < 2 \Rightarrow \sqrt 1 < \sqrt 2 \Leftrightarrow 1 < \sqrt 2 \). Vậy \(A < \sqrt 2 \). b) Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = - 5\\2x + y = 11\end{array} \right.\). \(\left\{ \begin{array}{l}x - y = - 5\\2x + y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\x - y = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2 - y = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 7\end{array} \right.\) Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2;7} \right)\). Bài 2: Phương pháp: 1. a) Lập bảng giá trị và vẽ đồ thị hàm số b) Đường thẳng \(\left( d \right):y = ax + b\,\,\) và đường thẳng \(\left( {d'} \right):y = a'x + b'\) song song với nhau khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) Đường thẳng \(\left( d \right):y = ax + b\,\,\)tiếp xúc với parabol \(\left( P \right):y = p{x^2}\) khi phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) có nghiệm kép. 2. a) Thay \(x = - 1\) vào phương trình ta tìm được \(m.\) Giải phương trình với \(m\) tìm được ta tính được nghiệm còn lại. b) Biến đổi để có tổng và tích hai nghiệm, sau đó sử dụng hệ thức Vi-ét. Cách giải: 1. Cho parabol \(\left( P \right):y = - {x^2}\) và đường thẳng \(\left( d \right):y = x - 2\) a) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\) Bảng giá trị của hàm số\(y = - {x^2}\)
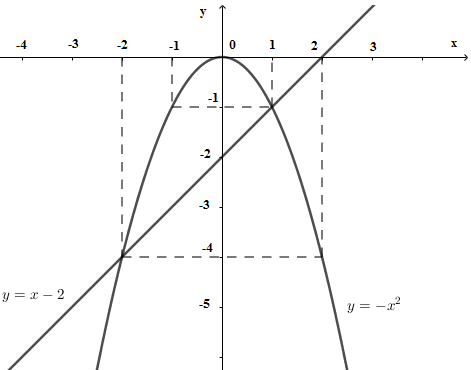
Vẽ đường cong qua các điểm có tọa độ \(\left( { - 2; - 4} \right),\left( { - 1; - 1} \right),\left( {0;0} \right),\left( {1; - 1} \right),\left( {2; - 4} \right)\) ta được parabol \(\left( P \right):y = - {x^2}\) và parabol nhận trục tung làm trục đối xứng. Bảng giá trị của hàm số \(y = x - 2\)
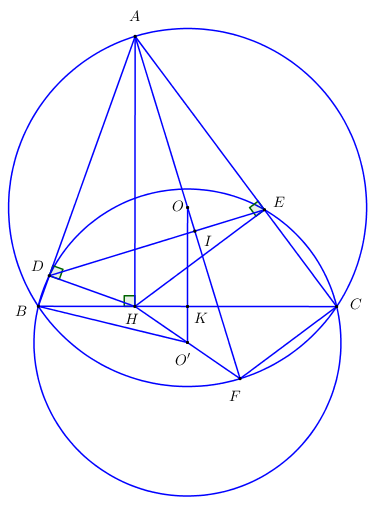
Vẽ đường thẳng đi qua hai điểm có tọa độ \(\left( {2;0} \right),\left( {0; - 2} \right)\) ta được đường thẳng \(\left( d \right):y = x - 2\) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\) b) Viết phương trình đường thẳng \(\left( {d'} \right)\) song song với \(\left( d \right)\) và tiếp xúc với \(\left( P \right).\) Gọi phương trình đường thẳng \(\left( {d'} \right):y = ax + m\) . Vì \(\left( {d'} \right)//\left( d \right)\) nên \(\left\{ \begin{array}{l}a = 1\\m \ne - 2\end{array} \right.\) suy ra \(\left( {d'} \right):y = x + m\). Xét phương trình hoành độ giao điểm của đường thẳng \(\left( {d'} \right)\) và parabol \(\left( P \right)\) ta có \( - {x^2} = x + m \Leftrightarrow {x^2} + x + m = 0\) (*) Để đường thẳng \(\left( {d'} \right)\) tiếp xúc với parabol \(\left( P \right)\) thì phương trình (*) có nghiệm kép \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\,\,\left( {luon\,\,dung} \right)\\1 - 4m = 0\end{array} \right. \Leftrightarrow m = \dfrac{1}{4}\,\,\left( {tm} \right)\) Vậy phương trình đường thẳng \(\left( {d'} \right):y = x + \dfrac{1}{4}\). 2. Cho phương trình \({x^2} - 4x + m = 0\) (1) (\(m\) là tham số) a) Biết phương trình có một nghiệm bằng \( - 1.\) Tính nghiệm còn lại. Thay \(x = - 1\) vào phương trình (1) ta được \({\left( { - 1} \right)^2} - 4.\left( { - 1} \right) + m = 0 \Leftrightarrow 5 + m = 0 \Leftrightarrow m = - 5\) Thay \(m = - 5\) vào phương trình (1) ta có phương trình : \(\begin{array}{l}\,\,\,\,\,\,{x^2} - 4x - 5 = 0 \Leftrightarrow {x^2} + x - 5x - 5 = 0\\ \Leftrightarrow x\left( {x + 1} \right) - 5\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 5\end{array} \right.\end{array}\) Vậy nghiệm còn lại là \(x = 5.\) b) Xác định \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(\left( {3{x_1} + 1} \right)\left( {3{x_2} + 1} \right) = 4\) Xét phương trình (1) có \(\Delta ' = {\left( { - 2} \right)^2} - 1.m = 4 - m\) Để phương trình (1) có hai nghiệm \({x_1},{x_2}\) thì \(\left\{ \begin{array}{l}a \ne 0\\\Delta ' \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\,\,\,\left( {luon\,\,dung} \right)\\4 - m \ge 0\end{array} \right. \Leftrightarrow m \le 4\) Khi đó, theo hệ thức Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}.{x_2} = m\end{array} \right.\) Theo bài ra ta có: \(\begin{array}{l}\left( {3{x_1} + 1} \right)\left( {3{x_2} + 1} \right) = 4 \Leftrightarrow 9{x_1}{x_2} + 3\left( {{x_1} + {x_2}} \right) + 1 = 4\\ \Leftrightarrow 9m + 3.4 - 3 = 0 \Leftrightarrow 9m + 9 = 0 \Leftrightarrow m = - 1\,\,\left( {tm} \right)\end{array}\) Vậy \(m = - 1\) là giá trị cần tìm. Bài 3: Phương pháp: +) Gọi số sản phẩm mỗi ngày đội công nhân làm được theo kế hoạch là x (sản phẩm) \(\left( {x \in \mathbb{N}*} \right)\). Tính số sản phẩm mỗi ngày đội công nhân làm được thực tế. +) Tính số ngày hoàn thành công việc theo kế hoạch và thực tế. +) Dựa vào giả thiết “đã hoàn thành công việc sớm hơn 1 ngày”, lập và giải phương trình. +) Đối chiếu điều kiện và kết luận. Cách giải: Gọi số sản phẩm mỗi ngày đội công nhân làm được theo kế hoạch là x (sản phẩm) \(\left( {x \in \mathbb{N}*} \right)\). Khi đó số sản phẩm mỗi ngày đội công nhân làm được thực tế là \(x + 5\) (sản phẩm). Số ngày làm hết 250 sản phẩm theo kế hoạch là \(\dfrac{{250}}{x}\) (ngày). Trong 4 ngày đầu đội công nhân làm được: \(4x\) (sản phẩm). Số sản phẩm cần làm thêm để hoàn thành kế hoạch là \(250 - 4x\) (sản phẩm). Số ngày làm xong \(250 - 4x\) sản phẩm là \(\dfrac{{250 - 4x}}{{x + 5}}\) (ngày). Do đội đó hoàn thành công việc sớm hơn 1 ngày nên ta có phương trình : \(\begin{array}{l}\,\,\,\,\,\,\dfrac{{250}}{x} - 1 = 4 + \dfrac{{250 - 4x}}{{x + 5}} \Leftrightarrow \dfrac{{250}}{x} - \dfrac{{250 - 4x}}{{x + 5}} = 5\\ \Leftrightarrow \dfrac{{250\left( {x + 5} \right) - x\left( {250 - 4x} \right)}}{{x\left( {x + 5} \right)}} = 5\\ \Leftrightarrow 250x + 1250 - 250x + 4{x^2} = 5{x^2} + 25x\\ \Leftrightarrow {x^2} + 25x - 1250 = 0\\ \Leftrightarrow {x^2} - 25x + 50x - 1250 = 0\\ \Leftrightarrow x\left( {x - 25} \right) + 50\left( {x - 25} \right) = 0\\ \Leftrightarrow \left( {x - 25} \right)\left( {x + 50} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 25 = 0\\x + 50 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 25\,\,\,\,\,\,\left( {tm} \right)\\x = - 50\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy số sản phẩm mỗi ngày đội công nhân làm được theo kế hoạch là 25 sản phẩm. Bài 4: Phương pháp: a) Chứng minh tứ giác nội tiếp bằng các dấu hiệu nhận biết. b) Sử dụng hệ thức lượng trong tam giác vuông để chứng minh đẳng thức. Cách giải: a) Chứng minh các tứ giác \(AEHD\) và \(BDEC\) nội tiếp được đường tròn. Xét tứ giác \(AEHD\) ta có: \(\left\{ \begin{array}{l}\angle ADH = {90^{0\,\,\,}}\left( {HD \bot AB} \right)\\\angle AEH = {90^0}\,\,\left( {HE \bot AC} \right)\end{array} \right. \Rightarrow \angle ADH + \angle AEH = {90^0} + {90^0} = {180^0}\) Mà hai góc này là hai góc đối diện \( \Rightarrow AEHD\) là tứ giác nội tiếp (dhnb). Vì tứ giác \(AEHD\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle ADE = \angle AHE\) (hai góc nội tiếp cùng chắn cung \(AE\)). Lại có \(\angle AHE = \angle ACH = \angle ECB\) (cùng phụ với \(\angle CHE\)) \( \Rightarrow \angle ADE = \angle ECB\) . \( \Rightarrow BDEC\) là tứ giác nội tiếp (tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện). (đpcm) b) Vẽ đường kính \(AF\) của đường tròn \(\left( O \right).\) Chứng minh \(BC = \sqrt {AB.BD} + \sqrt {AC.CE} \) và \(AF \bot DE.\) +) Áp dụng hệ thức lượng trong \(\Delta AHC\) vuông tại \(H\) có đường cao \(HE\) ta có: \(H{C^2} = CE.AC \Leftrightarrow HC = \sqrt {CE.AC} .\) Áp dụng hệ thức lượng trong \(\Delta AHB\) vuông tại \(H\) có đường cao \(HD\) ta có: \(B{H^2} = BD.BA \Leftrightarrow BH = \sqrt {BD.BA} .\) Mà \(BH + HC = BC\)\( \Leftrightarrow BC = \sqrt {AB.BD} + \sqrt {AC.CE} \,\,\,\left( {dpcm} \right).\) +) Chứng minh \(AF \bot DE:\) Gọi \(I = DE \cap AF\). Tứ giác \(BDEC\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle AED = \angle ABC\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp). Mà \(\angle ABC = \angle AFC\) (hai góc nội tiếp cùng chắn cung \(AC\)) \( \Leftrightarrow \angle AED = \angle AFC\). Ta có \(\angle ACF = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ACF\) vuông tại \(C\). \( \Leftrightarrow \angle CAF + \angle AFC = {90^0} \Rightarrow \angle EAI + \angle AED = {90^0}\). \( \Rightarrow \Delta AIE\) vuông tại \(I \Rightarrow AF \bot DE\). c) Gọi \(O'\) là tâm đường tròn ngoại tiếp \(\Delta BDE.\) Chứng minh \(O'\) là trung điểm của đoạn thẳng \(HF.\) Gọi \(K\) là trung điểm của \(BC\) \( \Rightarrow O'K \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung). Lại có \(OK \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung). \( \Rightarrow O;\,\,O';\,\,K\) thẳng hàng \( \Rightarrow OO' \bot BC\). Mà \(AH \bot BC \Rightarrow OO'//BC\). Xét tam giác \(AHF\) có: \(O\) là trung điểm của \(AF\); \(OO'//AH\,\,\left( {cmt} \right)\); \( \Rightarrow O'\) là trung điểm của \(HF\) (định lí đường trung bình của tam giác) (đpcm). d) Tính bán kính của đường tròn \(\left( {O'} \right)\) biết \(BC = 8cm,\,\,DE = 6cm,\,\,AF = 10cm.\) Bài 5: Phương pháp: Gọi \(O\) là tâm hình vuông. Tính các diện tích \({S_1},{S_2}\) bằng cách sử dụng mối quan hệ giữa diện tích các hình. Từ đó suy ra tỉ số. Cách giải: Gọi \(O\) là giao điểm của \(AC\) và \(BD\), gọi \(E,F\) là trung điểm của \(AB\) và \(AD\). Suy ra \(AC \bot BD\) tại \(O\) \( \Rightarrow \angle AOB = \angle AOD = {90^0}\) \( \Rightarrow O\) nằm trên các đường tròn đường kính \(AB\) và đường tròn đường kính \(AD\) (cùng nhìn \(AB\) và \(AD\) dưới các góc vuông). Không mất tính tổng quát, giả sử hình vuông có cạnh bằng \(2\) suy ra \(AC = BD = 2\sqrt 2 \). \( \Rightarrow OA = OB = OC = OD = \dfrac{{AC}}{2} = \sqrt 2 \). Ta có \(OE\) là đường trung bình của tam giác \(ABD \Rightarrow OE//AD \Rightarrow OE \bot AB\) . Xét tam giác \(EAO\) vuông tại \(E\) có \({S_{EOA}} = \dfrac{1}{2}EA.EO = \dfrac{1}{2}.1.1 = \dfrac{1}{2}\). Diện tích hình quạt \({S_{qEOA}} = \dfrac{{\pi E{O^2}.90}}{{360}} = \dfrac{\pi }{4}\) \( \Rightarrow \) Diện tích hình viên phân giới hạn bởi dây \(OA\) và cung \(OA\) trong hình tròn đường kính \(AB\) là \({S_{vpOA}} = {S_{qEOA}} - {S_{\Delta EOA}} = \dfrac{\pi }{4} - \dfrac{1}{2}\). Tương tự, diện tích hình viên phân giới hạn bởi dây \(OA\) và cung \(OA\) trong hình tròn đường kính \(AD\) là \({S_{vpOA}} = \dfrac{\pi }{4} - \dfrac{1}{2}\). Suy ra \({S_1} = 2{S_{vpOA}} = 2\left( {\dfrac{\pi }{4} - \dfrac{1}{2}} \right) = \dfrac{\pi }{2} - 1\). Diện tích tam giác \(BOC\) là \({S_{\Delta BOC}} = \dfrac{1}{2}OB.OC = \dfrac{1}{2}.\sqrt 2 .\sqrt 2 = 1\). CMTT: Diện tích hình viên phân giới hạn bởi dây \(OB\) và cung \(OB\) là \({S_{vpOB}} = \dfrac{\pi }{4} - \dfrac{1}{2}\) Diện tích phần còn lại giới hạn tam giác \(OBC\) và hình viên phân giới hạn bởi dây \(OB\) và cung \(OB\) là \({S_3} = {S_{\Delta OBC}} - {S_{vpOB}} = 1 - \dfrac{\pi }{4} + \dfrac{1}{2} = \dfrac{3}{2} - \dfrac{\pi }{4}\). Tương tự, diện tích phần còn lại giới hạn tam giác \(ODC\) và hình viên phân giới hạn bởi dây \(OD\) và cung \(OD\) là \({S_4} = {S_{\Delta ODC}} - {S_{vpOD}} = 1 - \dfrac{\pi }{4} + \dfrac{1}{2} = \dfrac{3}{2} - \dfrac{\pi }{4}\) Suy ra \({S_2} = {S_3} + {S_4} = 2\left( {\dfrac{3}{2} - \dfrac{\pi }{4}} \right) = 3 - \dfrac{\pi }{2}\) \( \Rightarrow \) \(\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{\dfrac{\pi }{2} - 1}}{{3 - \dfrac{\pi }{2}}} = \dfrac{{\pi - 2}}{2}:\dfrac{{6 - \pi }}{2} = \dfrac{{\pi - 2}}{{6 - \pi }}\). Vậy \(\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{\pi - 2}}{{6 - \pi }}\).
|




















Danh sách bình luận