Đề số 3 - Đề thi vào lớp 10 môn ToánĐề thi vào lớp 10 môn Toán - Đề số 3 có đáp án và lời giải chi tiết Quảng cáo
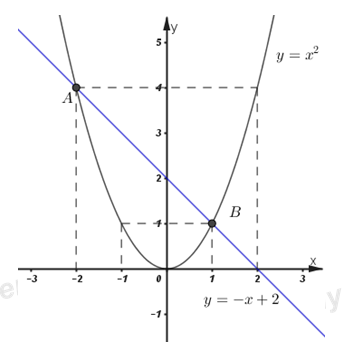
Đề bài Câu 1. (2,0 điểm) 1. Tính giá trị của các biểu thức \(M = \sqrt {36} + \sqrt {25} \) \(N = \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} - \sqrt 5 \) 2. Cho biểu thức \(P = 1 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}},\) với \(x \ge 0\) và \(x \ne 1\) a) Rút gọn biểu thức P b) Tìm giá trị của x, biết P > 3 Câu 2. (2 điểm) 1) Cho parabol \(\left( P \right):\;y = {x^2}\) và đường thẳng \(\left( d \right):\;y = - x + 2.\) a) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng một mặt phẳng tọa độ Oxy. b) Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính. 2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}3x + y = 5\\2x - y = 10\end{array} \right..\) Câu 3. (2,5 điểm) 1) Cho phương trình \({x^2} - 2mx + 2m - 1 = 0\) (m là tham số) (1) a) Giải phương trình (1) với \(m = 2.\) b) Tìm \(m\) để phương trình (1) có hai nghiệm \({x_1},\;{x_2}\) sao cho: \(\left( {x_1^2 - 2m{x_1} + 3} \right)\left( {x_2^2 - 2m{x_2} - 2} \right) = 50.\) 2) Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A đến B. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10 km/h, nên xe thứ nhất đến B trước xe thứ hai 15 phút. Tính vận tốc của mỗi xe. Câu 4. (1,0 điểm): Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết AC = 8cm và BC = 10 cm. Tính độ dài AB, BH, CH và AH. Câu 5. (2,5 điểm) Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D; O và B nằm về hai phía so với cát tuyến MCD). a) Chứng minh tứ giác MAOB nội tiếp. b) Chứng minh \(M{B^2} = MC.MD\) c) Gọi H là giao điểm của AB và OM. Chứng minh AB là phân giác của \(\widehat {CHD}\). Lời giải chi tiết Câu 1. 1. Tính giá trị của các biểu thức \(M = \sqrt {36} + \sqrt {25} \) \(N = \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} - \sqrt 5 \) Ta có: \(M = \sqrt {36} + \sqrt {25} \) \(\;\;\;\;\;= \sqrt {{6^2}} + \sqrt {{5^2}} = 6 + 5 = 11\) \(N = \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} - \sqrt 5 \) \(\;\;\;\;\;= \left| {\sqrt 5 - 1} \right| - \sqrt 5\) \(\;\;\;\;\; = \sqrt 5 - 1 - \sqrt 5 \) \(\;\;\;\;\;= - 1\,\,\left( {Do\,\sqrt 5 - 1 > 0\,\,} \right)\) 2. Cho biểu thức \(P = 1 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}},\) với \(x \ge 0\) và \(x \ne 1\) a) Rút gọn biểu thức P Với \(x \ge 0\) và \(x \ne 1\) ta có: \(\begin{array}{l}P = 1 + \dfrac{{x - \sqrt x }}{{\sqrt x - 1}}\\\,\,\,\,\, = 1 + \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x - 1}}\\\,\,\,\,\, = 1 + \sqrt x \end{array}\) b) Tìm giá trị của x, biết P > 3 \(P > 3 \Leftrightarrow 1 + \sqrt x > 3 \Leftrightarrow \sqrt x > 2 \Leftrightarrow x > 4\) Kết hợp với điều kiện: \(x \ge 0\) và \(x \ne 1\) ta được \(x > 4\) Vậy với \(x > 4\) thì \(P > 3\) Câu 2: 1) Cho parabol \(\left( P \right):\;\;y = {x^2}\) và đường thẳng \(\left( d \right):\;\;y = - x + 2.\) a) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng một mặt phẳng tọa độ Oxy. +) Vẽ đồ thị hàm số: \(\left( d \right):\;\;y = - x + 2.\)
+) Vẽ đồ thị hàm số: \(\left( P \right):\;\;y = {x^2}.\)
Đồ thị hàm số:
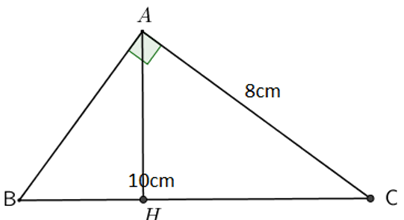
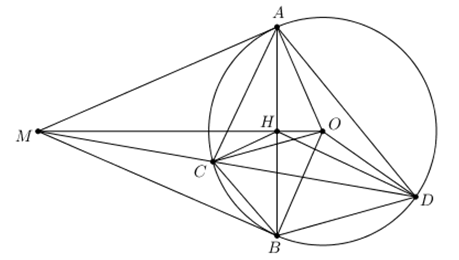
b) Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính. Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm. Ta có phương trình hoành độ giao điểm của hai đồ thị là: \(\begin{array}{l}\;\;\; - x + 2 = {x^2}\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = 4\\x = 1 \Rightarrow y = 1\end{array} \right..\end{array}\) Vậy hai đồ thị cắt nhau tại hai điểm phân biệt \(A\left( { - 2;\;4} \right)\) và \(B\left( {1;\;1} \right).\) 2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}3x + y = 5\\2x - y = 10\end{array} \right..\) \(\left\{ \begin{array}{l}3x + y = 5\\2x - y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 10\\5x = 15\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2.3 - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 4\end{array} \right..\) Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\;y} \right) = \left( {3; - 4} \right).\) Câu 3: 1) Cho phương trình \({x^2} - 2mx + 2m - 1 = 0\) (m là tham số) (1) a) Giải phương trình (1) với \(m = 2.\) Thay \(m = 2\) vào phương trình \(\left( 1 \right)\) ta được: \(\begin{array}{l}\left( 1 \right) \Leftrightarrow {x^2} - 4x + 3 = 0\\ \Leftrightarrow {x^2} - 3x - x + 3 = 0\\ \Leftrightarrow x\left( {x - 3} \right) - \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right..\end{array}\) Vậy với \(m = 2\) thì phương trình có tập nghiệm \(S = \left\{ {1;\;3} \right\}.\) b) Tìm \(m\) để phương trình (1) có hai nghiệm \({x_1},\;{x_2}\) sao cho: \(\left( {x_1^2 - 2m{x_1} + 3} \right)\left( {x_2^2 - 2m{x_2} - 2} \right) = 50.\) Phương trình (1) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\) \(\begin{array}{l} \Leftrightarrow {m^2} - 2m + 1 > 0\\ \Leftrightarrow {\left( {m - 1} \right)^2} > 0\\ \Leftrightarrow m - 1 \ne 0\\ \Leftrightarrow m \ne 1.\end{array}\) Với \(m \ne 1\) thì phương trình (1) có hai nghiệm phân biệt \({x_1},\;\;{x_2}.\) Khi đó ta có: \(\left\{ \begin{array}{l}x_1^2 - 2m{x_1} + 2m - 1 = 0\\x_1^2 - 2m{x_1} + 2m - 1 = 0\end{array} \right..\) Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = 2m - 1\end{array} \right..\) Theo đề bài ta có: \(\left( {x_1^2 - 2m{x_1} + 3} \right)\left( {x_2^2 - 2m{x_2} - 2} \right) = 50\) \(\begin{array}{l} \Leftrightarrow \left( {x_1^2 - 2m{x_1} + 2m - 1 - 2m + 4} \right)\left( {x_2^2 - 2m{x_2} + 2m - 1 - 2m - 1} \right) = 50\\ \Leftrightarrow \left( {4 - 2m} \right)\left( { - 2m - 1} \right) = 50\\ \Leftrightarrow \left( {2m - 4} \right)\left( {2m + 1} \right) = 50\\ \Leftrightarrow \left( {m - 2} \right)\left( {2m + 1} \right) = 25\\ \Leftrightarrow 2{m^2} + m - 4m - 2 = 25\\ \Leftrightarrow 2{m^2} - 3m - 27 = 0\\ \Leftrightarrow 2{m^2} - 9m + 6m - 27 = 0\\ \Leftrightarrow m\left( {2m - 9} \right) + 3\left( {2m - 9} \right) = 0\\ \Leftrightarrow \left( {2m - 9} \right)\left( {m + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2m - 9 = 0\\m + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{9}{2}\;\;\left( {tm} \right)\\m = - 3\;\;\left( {tm} \right)\end{array} \right..\end{array}\) Vậy \(m = \dfrac{9}{2}\) và \(m = - 3\) thỏa mãn điều kiện bài toán. 2) Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A đến B. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10 km/h, nên xe thứ nhất đến B trước xe thứ hai 15 phút. Tính vận tốc của mỗi xe. Gọi vận tốc của xe thứ nhất là \(x\;\left( {km/h} \right)\;\;\left( {x > 10} \right).\) \( \Rightarrow \) Vận tốc của xe thứ hai là: \(x - 10\;\;\left( {km/h} \right).\) Thời gian xe thứ nhất đi từ A đến B là \(\dfrac{{50}}{x}\,\,\left( h \right)\) ; Thời gian xe thứ hai đi từ A đến B là: \(\dfrac{{50}}{{x - 10}}\;\;\left( h \right).\) Vì xe thứ nhất đến B trước xe thứ hai 15 phút = \(\dfrac{1}{4}h\) nên ta có phương trình: \(\dfrac{{50}}{{x - 10}} - \dfrac{{50}}{x} = \dfrac{1}{4}\) \(\begin{array}{l} \Leftrightarrow 4.50.x - 4.50\left( {x - 10} \right) = x\left( {x - 10} \right)\\ \Leftrightarrow 200x - 200x + 2000 = {x^2} - 10x\\ \Leftrightarrow {x^2} - 10x - 2000 = 0\\ \Leftrightarrow {x^2} - 50x + 40x - 2000 = 0\\ \Leftrightarrow x\left( {x - 50} \right) + 40\left( {x - 50} \right) = 0\\ \Leftrightarrow \left( {x - 50} \right)\left( {x + 40} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 50 = 0\\x + 40 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 50\;\;\left( {tm} \right)\\x = - 40\;\;\left( {ktm} \right)\end{array} \right..\end{array}\) Vậy vận tốc của xe thứ nhất là \(50\;km/h\) và vận tốc xe thứ hai là \(50 - 10 = 40\;km/h.\) Câu 4. Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết AC = 8cm và BC = 10 cm. Tính độ dài AB, BH, CH và AH. +) Tính AB Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có: \(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Rightarrow A{B^2} = B{C^2} - A{C^2} = {10^2} - {8^2} = 36\\ \Rightarrow AB = 6\left( {cm} \right)\end{array}\) +) Tính BH Áp dụng hệ thức lượng trong tam giác vuông ABC có: \(A{B^2} = BH.BC\) \(\Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{6^2}}}{{10}} = 3,6\left( {cm} \right)\) +) Tính CH Áp dụng hệ thức lượng trong tam giác vuông ABC có: \(A{C^2} = CH.BC \) \(\Rightarrow CH = \dfrac{{A{C^2}}}{{BC}} = \dfrac{{{8^2}}}{{10}} = 6,4\left( {cm} \right)\) +) Tính AH Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: \(A{H^2} = BH.CH = 3,6.6,4 = 23,04\) \( \Rightarrow AH = 4,8\left( {cm} \right)\) Câu 5. a) Chứng minh tứ giác MAOB nội tiếp. Ta có \(\widehat {OAM} = \widehat {OBM} = {90^0}\) (Do MA, MB là tiếp tuyến của đường tròn (O)) Xét tứ giác OAMB có: \(\widehat {OAM} + \widehat {OBM} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác OAMB là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800). b) Chứng minh \(M{B^2} = MC.MD\) Xét tam giác MBC và tam giác MDB có: \(\widehat {BMD}\) chung; \(\widehat {MBC} = \widehat {MDB}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BC) \( \Rightarrow \Delta MBC \sim \Delta MDB\,\,\left( {g.g} \right) \) \(\Rightarrow \dfrac{{MB}}{{MD}} = \dfrac{{MC}}{{MB}}\) \(\Rightarrow M{B^2} = MC.MD\) c) Gọi H là giao điểm của AB và OM. Chứng minh AB là phân giác của \(\widehat {CHD}\). Ta có \(MA = MB\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của AB; \(OA = OB\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của AB; \( \Rightarrow OM\) là trung trực của AB \( \Rightarrow OM \bot AB\) Xét tam giác vuông OMB có \(M{B^2} = MH.MO\) (hệ thức lượng trong tam giác vuông). Mà \(M{B^2} = MC.MD\,\,\left( {cmt} \right) \) \(\Rightarrow MH.MO = MC.MD\) \(\Rightarrow \dfrac{{MC}}{{MO}} = \dfrac{{MH}}{{MD}}\) Xét tam giác MCH và MOD có : \(\widehat {OMD}\) chung ; \(\dfrac{{MC}}{{MO}} = \dfrac{{MH}}{{MD}}\,\,\,\left( {cmt} \right)\); \(\Delta MCH \sim \Delta MOD\,\,\left( {c.g.c} \right) \) \(\Rightarrow \widehat {MHC} = \widehat {MDO}\) (hai góc tương ứng) (1). Mà \(\widehat {MHC} + \widehat {OHC} = {180^0}\) \( \Rightarrow \widehat {MDO} + \widehat {OHC} = {180^0} \Rightarrow \) Tứ giác OHCD là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800). \( \Rightarrow \widehat {OHD} = \widehat {OCD}\) (2) (hai góc nội tiếp cùng chắn cung OD). Mà \(\widehat {OCD} = \widehat {ODC} = \widehat {MDO}\) (3) (tam giác OCD cân tại O); Từ (1), (2) và (3) \( \Rightarrow \widehat {MHC} = \widehat {OHD}\). \( \Rightarrow {90^0} - \widehat {MHC} = {90^0} - \widehat {OHD} \) \(\Rightarrow \widehat {CHB} = \widehat {BHD}\). Vậy HB là tia phân giác của góc CHD hay AB là tia phân giác của góc CHD. Loigiaihay.com
|




















Danh sách bình luận