Đề thi vào 10 môn Toán Trà Vinh năm 2021Tải vềCâu 1 (1,0 điểm): Giải hệ phương trình Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
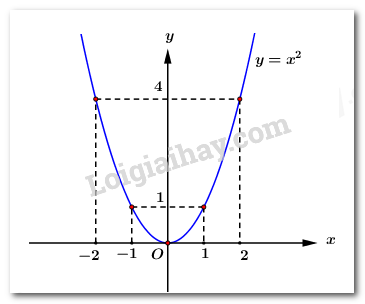
Đề bài Câu 1 (1,0 điểm): Giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y = 4\\x + 3y = - 5\end{array} \right.\). Câu 2 (2,0 điểm): Trong mặt phẳng tọa độ \(Oxy\), cho parabol \(\left( P \right):\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,y = mx + 3\) (\(m\)là tham số). 1. Vẽ parabol \(\left( P \right)\). 2. Khi \(m = 2\), tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính. 3. Tìm m để đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) luôn cắt nhau tại hai điểm phân biệt có hoành độ \({x_1},\,\,{x_2}\) thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{3}{2}\). Câu 3 (1,0 điểm): Rút gọn biểu thức \(A = \sqrt {24} + 2\sqrt {54} - 2\sqrt {96} \) Câu 4 (1,0 điểm): Giải phương trình \(4{x^2} + 7x - 2 = 0\) Câu 5 (1,0 điểm): Tổng số học sinh của hai lớp \(9A\) và \(9B\) ở một trường trung học cơ sở là \(76\) học sinh. Hưởng ứng phong trào ủng hộ trang thiết bị y tế trong đợt phòng dịch Covid-\(19\), cả hai lớp đã quyên góp ủng hộ \(189\) chiếc khẩu trang. Biết rằng mỗi học sinh lớp \(9A\) ủng hộ \(3\) chiếc khẩu trang, mỗi học sinh lớp \(9B\) ủng hộ \(2\) chiếc khẩu trang. Tính số học sinh của mỗi lớp. Câu 6 (3,0 điểm): Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right)\). Các đường cao \(AD\,\,\left( {D \in BC} \right)\), \(BE\,\,\left( {E \in AC} \right)\) và \(CF\,\,\left( {F \in AB} \right)\) cắt nhau tại \(H\). 1. Chứng minh tứ giác \(BCEF\) nội tiếp đường tròn; 2. Chứng minh \(DA\) là tia phân giác của \(\angle EDF\); 3. Kẻ đường kính \(AK\), gọi \(I\) là trung điểm của \(BC\). Chứng minh ba điểm \(H,\,\,I,\,\,K\) thẳng hàng. Câu 7 (1,0 điểm): Tìm cặp số \(\left( {x,y} \right)\) thỏa mãn phương trình \(8x - 4{x^2} + 2y - 5 = 0\) sao cho \(y\) đạt giá trị nhỏ nhất. Lời giải Câu 1 (VD): Phương pháp: Vận dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình Cách giải: Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}2x - y = 4\\x + 3y = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = 4\\2x + 6y = - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7y = - 14\\x = - 5 - 3y\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = - 2\\x = - 5 - 3.\left( { - 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - 2\\x = 1\end{array} \right.\end{array}\) Vậy hệ phương trình đã cho có nghiệm \(\left( {x;y} \right) = \left( {1; - 2} \right)\). Câu 2 (VD): Phương pháp: 1) Lập bảng giá trị để vẽ đồ thi hàm số 2) Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\), đưa về phương trình bậc hai một ẩn sau đó giải phương trình để tìm nghiệm và suy ra giao điểm 3) Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\), đưa về phương trình bậc hai một ẩn, yêu cầu đề bài được đưa về tìm m để phương trình có hai nghiệm phân biệt thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{3}{2}\). Cách giải: 1) Parabol \(\left( P \right):\,\,y = {x^2}\) có bề lõm hướng lên và nhận \(Oy\) làm trục đối xứng. Ta có bảng giá trị sau:
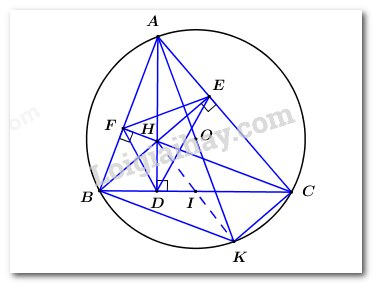
\( \Rightarrow \) Parabol \(\left( P \right):\,\,y = {x^2}\) đi qua các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\). Đồ thị Parabol \(\left( P \right):\,\,y = {x^2}\): 2) Khi \(m = 2\), đường thẳng \(\left( d \right)\) có dạng \(\left( d \right):\,\,y = 2x + 3\). Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm của phương trình: \({x^2} = 2x + 3 \Leftrightarrow {x^2} - 2x - 3 = 0\). Ta có \(a - b + c = 1 - \left( { - 2} \right) - 3 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = - 1\\{x_2} = \dfrac{{ - c}}{a} = 3\end{array} \right.\). Với \({x_1} = - 1 \Rightarrow {y_1} = x_1^2 = 1\) \( \Rightarrow A\left( { - 1;1} \right)\). Với \({x_2} = 3 \Rightarrow {y_2} = x_2^2 = 9 \Rightarrow B\left( {3;9} \right)\). Vậy khi \(m = 2\) thì \(\left( P \right)\) và \(\left( d \right)\) cắt nhau tại 2 điểm \(A\left( { - 1;1} \right)\) và \(B\left( {3;9} \right)\). 3) Xét phương trình hoành độ giao điểm \({x^2} = mx + 3 \Leftrightarrow {x^2} - mx - 3 = 0\,\,\,\left( * \right)\) Để \(\left( d \right)\) và \(\left( P \right)\) luôn cắt nhau tại 2 điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt. \( \Rightarrow \Delta = {m^2} - 4.1.\left( { - 3} \right) = {m^2} + 12 > 0\) (luôn đúng với mọi \(m\)). Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = - 3\end{array} \right.\). Theo bài ra ta có: \(\begin{array}{l}\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{3}{2} \Leftrightarrow \dfrac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \dfrac{3}{2}\\ \Leftrightarrow \dfrac{m}{{ - 3}} = \dfrac{3}{2} \Leftrightarrow m = - \dfrac{9}{2}\end{array}\) Vậy \(m = - \dfrac{9}{2}\) thỏa mãn yêu cầu bài toán. Câu 3 (VD): Phương pháp: Khai phương các số ở trong căn, sau đó tính giá trị của biểu thức Cách giải: Ta có: \(\begin{array}{l}A = \sqrt {24} + 2\sqrt {54} - 2\sqrt {96} \\A = \sqrt {{2^2}.6} + 2\sqrt {{3^2}.6} - 2\sqrt {{4^2}.6} \\A = 2\sqrt 6 + 2.3\sqrt 6 - 2.4\sqrt 6 \\A = 2\sqrt 6 + 6\sqrt 6 - 8\sqrt 6 \\A = 0\end{array}\) Vậy \(A = 0\). Câu 4 (VD): Phương pháp: Vận dụng công thức nghiệm để xác định nghiệm của phương trình bậc hai một ẩn Cách giải: Ta có: \(\Delta = {7^2} - 4.4.\left( { - 2} \right) = 49 + 32 = 81 > 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - b + \sqrt \Delta }}{{2a}} = \dfrac{{ - 7 + \sqrt {81} }}{{2.4}} = \dfrac{1}{4}\\{x_2} = \dfrac{{ - b - \sqrt \Delta }}{{2a}} = \dfrac{{ - 7 - \sqrt {81} }}{{2.4}} = - 2\end{array} \right.\) Vậy tập nghiệm của phương trình đã cho là \(S = \left\{ {\dfrac{1}{4}; - 2} \right\}\). Câu 5 (VD): Phương pháp: Gọi số học sinh của lớp \(9A,\,\,9B\) lần lượt là \(x,\,\,y\,\,\left( {x \in \mathbb{N}*,y \in \mathbb{N}*} \right)\), sau đó dựa vào giải thiết lâp hệ phương trình để tìm \(x,\,\,y\), đối chiếu điều kiện, kết luận. Cách giải: Gọi số học sinh của lớp \(9A,\,\,9B\) lần lượt là \(x,\,\,y\,\,\left( {x \in \mathbb{N}*,y \in \mathbb{N}*} \right)\)( học sinh) Tổng số học sinh lớp \(9A,\,\,9B\) là \(76\) học sinh nên ta có phương trình \(x + y = 76\,\,\,\,\,\,\,\,\left( 1 \right)\) Cả hai lớp đã quyên góp ủng hộ \(189\) chiếc khẩu trang. Biết rằng mỗi học sinh lớp \(9A\) ủng hộ \(3\) chiếc khẩu trang, mỗi học sinh lớp \(9B\) ủng hộ \(2\) chiếc khẩu trang nên ta có phương trình \(3x + 2y = 189\,\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right),\left( 2 \right)\) ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 76\\3x + 2y = 189\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2x + 2y = 152\\3x + 2y = 189\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 37\\y = 76 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 37\\y = 39\end{array} \right.\,\,\,\left( {tm} \right)\) Vậy số học sinh của lớp \(9A,\,\,9B\) lần lượt là \(37\) và \(37\) học sinh. Câu 6 (VD): Phương pháp: 1) Vận dụng dấu hiệu nhận biết tứ giác nội tiếp đường tròn: tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau 2) Vận dụng tính chất của tứ giác nối tiếp, suy ra các góc bằng nhau; dấu hiệu nhận biết phân giác của một góc 3) Chứng minh \(BHCK\) là hình bình hành, suy ra \(H,\,\,I,\,\,K\) thẳng hàng Cách giải: 1) Xét tứ giác \(BCEF\) có \(\angle BEC = \angle BFC = {90^0}\,\,\left( {gt} \right)\) nên \(BCEF\) là tứ giác nội tiếp (tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau). 2) Xét tứ giác \(BDHF\) có: \(\angle BDH + \angle BFH = {90^0} + {90^0} = {180^0}\) \( \Rightarrow BDHF\) là tứ giác nội tiếp (dhnb). \( \Rightarrow \angle HDF = \angle HBF = \angle EBA\) (2 góc nội tiếp cùng chắn cung \(HF\)). Xét tứ giác \(CDHE\) có: \(\angle CDH + \angle CEH = {90^0} + {90^0} = {180^0}\) \( \Rightarrow CDHE\) là tứ giác nội tiếp (dhnb). \( \Rightarrow \angle HDE = \angle HCE = \angle FCA\) (2 góc nội tiếp cùng chắn cung \(HE\)). Ta lại có: \(\left\{ \begin{array}{l}\angle EBA + \angle BAC = {90^0}\\\angle FCA + \angle BAC = {90^0}\end{array} \right.\) (do \(\Delta ABE,\,\,\Delta ACF\) là các tam giác vuông tại \(A\)) \( \Rightarrow \angle EBA = \angle FCA\). \( \Rightarrow \angle HDF = \angle HDE\). Vậy \(DA\) là tia phân giác của \(\angle EDF\). 3) Vì \(AK\) là đường kính của \(\left( O \right)\) nên \(\angle ABK = \angle ACK = {90^0}\) (góc nội tiếp chắn nửa đường tròn). Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}BK \bot AB\,\,\left( {cmt} \right)\\CH \bot AB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow BK//CH\\\left\{ \begin{array}{l}CK \bot AC\,\,\left( {cmt} \right)\\BH \bot AC\,\,\left( {gt} \right)\end{array} \right. \Rightarrow CK//BH\end{array}\) \( \Rightarrow BHCK\) là hình bình hành (tứ giác có các cặp cạnh đối song song). \( \Rightarrow \) Hai đường chéo \(BC\) và \(HK\) cắt nhau tại trung điểm mỗi đường (tính chất). Mà \(I\) là trung điểm của \(BC\,\,\left( {gt} \right)\), do đó \(I\) phải là trung điểm của \(HK\). Vậy \(H,\,\,I,\,\,K\) thẳng hàng (đpcm). Câu 7 (VDC): Phương pháp: 1) Biến đổi phương trình ban đầu về dạng \(y = f\left( x \right)\), vận dụng hằng đẳng thức để tìm giá trị nhỏ nhất của \(f\left( x \right)\) Cách giải: Ta có: \(\begin{array}{l}\,\,\,\,\,\,\,8x - 4{x^2} + 2y - 5 = 0\\ \Leftrightarrow 2y = 4{x^2} - 8x + 4 + 1\\ \Leftrightarrow 2y = 4\left( {{x^2} - 2x + 1} \right) + 1\\ \Leftrightarrow 2y = 4{\left( {x - 1} \right)^2} + 1\end{array}\) Nhận thấy \({\left( {x - 1} \right)^2} \ge 0\,\,\forall x \Rightarrow 4{\left( {x - 1} \right)^2} \ge 0\,\,\forall x \Rightarrow 4{\left( {x - 1} \right)^2} + 1 \ge 1\,\,\forall x\). Do đó ta có \(2y \ge 1\,\,\forall x \Leftrightarrow y \ge \dfrac{1}{2}\,\,\forall x\). \( \Rightarrow \) \(y\) đạt giá trị nhỏ nhất bằng \(\dfrac{1}{2}\) khi \(x - 1 = 0 \Leftrightarrow x = 1\). Vậy cặp \(\left( {x,y} \right)\) thỏa mãn yêu cầu bài toán là \(\left( {x;y} \right) = \left( {1;\dfrac{1}{2}} \right)\)
|




















Danh sách bình luận