Đề thi vào 10 môn Toán Phú Thọ năm 2021Tải vềPHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm) Câu 1. Điều kiện xác định của biểu thức Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm) Câu 1. Điều kiện xác định của biểu thức \(\sqrt {x - 5} \) là: A. \(x \ge 5\) B. \(x \le 5\) C. \(x > 5\) D. \(x < 5\) Câu 2. Với giá trị nào của \(m\) thì hai đường thẳng \(y = 12x + 5 - m\) và \(y = 3x + m + 3\) cắt nhau tại một điểm trên trục tung? A. \(5.\) B. \( - 3.\) C. \(1.\) D. \(4.\) Câu 3. Hàm số \(y = \left( {m + 2} \right)x + 4\) đồng biến trên \(\mathbb{R}\) khi A. \(m < - 2\) B. \(m \ge - 2\) C. \(m \ne - 2\) D. \(m > - 2\) Câu 4. Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + 3y = 10\\2x - y = - 1\end{array} \right.\) là A. \(\left( {3;1} \right)\) B. \(\left( {1;3} \right)\) C. \(\left( { - 1; - 3} \right)\) D. \(\left( { - 3; - 1} \right)\) Câu 5. Với giá trị nào của \(m\) thì đồ thị hàm số \(y = \left( {m - 2} \right){x^2}\) đi qua điểm \(A.(1;2)\)? A. \(0.\) B. \(2.\) C. \(4.\) D. \( - 2.\) Câu 6. Phương trình \({x^2} - 2x + m = 0\) có hai nghiệm phân biệt khi A. \(m > 1\) B. \(m = 1\) C. \(m \ge 1\) D. \(m < 1\) Câu 7. Phương trình nào sau đây vô nghiệm? A. \({x^2} + x + 1 = 0\) B. \({x^2} - 4x + 4 = 0\) C. \({x^2} + x - 1 = 0\) D. \({x^2} + 5x + 6 = 0\) Câu 8. Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AC = 5cm,\,\,HC = 4cm.\) Khi đó độ dài cạnh \(BC\) là A. \(9cm.\) B. \(\dfrac{{25}}{4}cm.\) C. \(\dfrac{{25}}{{16}}cm.\) D. \(\dfrac{5}{4}cm.\) Câu 9. Cho đường tròn tâm \(O\), bán kính \(R = 13(cm)\), dây cung \(AB = 24(cm)\). Khoảng cách từ tâm \(O\) đến dây \(AB\) là A. \(3\left( {cm} \right).\) B. \(4\left( {cm} \right).\) C. \(5\left( {cm} \right).\) D. \(6\left( {cm} \right).\) Câu 10. Cho tứ giác \(MNPQ\) nội tiếp một đường tròn. Biết \(\angle MNP = {60^0},\angle PMQ = {40^0}\). Số đo \(\angle MPQ\) bằng: (Tham khảo hình vẽ)
A. \({10^0}\) B. \({20^0}\) C. \({40^0}\) D. \({50^0}\) PHẦN II. TỰ LUẬN (7,5 điểm): Bài 1. (1,5 điểm) Cho biểu thức \(A = \dfrac{{ - 7\sqrt x + 6}}{{x - 4}} + \dfrac{{\sqrt x }}{{\sqrt x - 2}}.\left( {x \ge 0,\,x \ne 4} \right)\) a) Tính giá trị của biểu thức \(A\) khi \(x = 16\) b) Rút gọn biểu thức \(A\). Bài 2. (2,0 điểm) 1) (ID: 550946) Cho đường thẳng \(\left( d \right):y = 2mx + 2m - 3\) và Parabol \(\left( P \right):y = {x^2}\) a) Tìm \(m\) để đường thẳng \(\left( d \right)\) đi qua \(A\left( {1;5} \right).\) b) Tìm \(m\) để đường thẳng \(\left( d \right)\) tiếp xúc với Parabol \(\left( P \right)\) 2) Cho hệ phương trình \(\left\{ \begin{array}{l}2x - y = m - 1\\3x + y = 4m + 1\end{array} \right.\) (\(m\) là tham số) a) Giải hệ phương trình với \(m = 2\) b) Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right)\) thỏa mãn \(2{x^2} - 3y = 2\) Bài 3. (3,0 điểm) Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Trên tia đối tia \(BA\) lấy điểm \(C(C\) không trùng với \(B)\). Kẻ tiếp tuyến \(CD\) với đường tròn \(\left( O \right)\) (\(D\) là tiếp điểm), tiếp tuyến tại \(A\) của đường tròn \(\left( O \right)\) cắt đường thẳng \(CD\) tại \(E\). a) Chứng minh rằng tứ giác \(AODE\) nội tiếp. b) Gọi \(H\) là giao điểm của \(AD\) và \(OE,K\) là giao điểm của \(BE\) với đường tròn \(\left( O \right)\) (\(K\) không trùng với \(B\)). Chứng minh \(\angle EHK = \angle KBA\) c) Đường thẳng vuông góc với \(AB\) tại \(O\) cắt \(CE\) tại \(M\). Chứng minh \(\dfrac{{EA}}{{EM}} - \dfrac{{MO}}{{MC}} = 1\) Bài 4. (1,0 điểm) Cho \(a,b,c\) là các số dương thỏa mãn \({a^2} + {b^2} + {c^2} = 1\). Tìm giá trị lớn nhất của biểu thức \(A = \left( {1 + 2a} \right)\left( {1 + 2bc} \right)\). Lời giải chi tiết PHẦN I. TRẮC NGHIỆM KHÁCH QUAN BẢNG ĐÁP ÁN
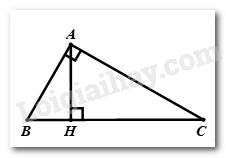
Câu 1 Phương pháp: Biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0\) Cách giải: Điều kiện xác định của biểu thức \(\sqrt {x - 5} \) là \(x - 5 \ge 0 \Leftrightarrow x \ge 5\) Chọn A. Câu 2 Phương pháp: Tìm điều kiện để hai đường thẳng cắt nhau Tọa độ giao điểm thuộc trục tung có dạng \(\left( {0;a} \right)\) Cách giải: Phương trình hoành độ giao điểm của hai đường thẳng là: \(\begin{array}{l}\,\,\,\,\,\,\,\,12x + 5 - m = 3x + m + 3\\ \Leftrightarrow 9x = 2m - 2\\ \Leftrightarrow x = \dfrac{{2m - 2}}{9}\end{array}\) Để giao điểm của hai đường thẳng trục tung \( \Leftrightarrow \dfrac{{2m - 2}}{9} = 0 \Leftrightarrow m = 1\) Vậy \(m = 1\) thì hai đường thẳng cắt nhau tại một điểm trên trục tung Chọn C. Câu 3 Phương pháp: Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\) Cách giải: Hàm số \(y = \left( {m + 2} \right)x + 4\) đồng biến trên \(\mathbb{R}\) khi \(m + 2 > 0 \Leftrightarrow m > - 2\) Chọn A. Câu 4 Phương pháp: Sử dụng phương pháp cộng đại số, tìm được nghiệm \(y\) Sử dụng phương pháp thế, tìm được nghiệm \(x\) Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình. Cách giải: \(\left\{ \begin{array}{l}x + 3y = 10\\2x - y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 6y = 20\\2x - y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7y = 21\\2x - y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\2x - 3 = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x = 1\end{array} \right.\) Vậy nghiệm của hệ là \(\left( {x;y} \right) = \left( {1;3} \right)\) Chọn B. Câu 5 Phương pháp: Đồ thị hàm số \(\left( P \right):y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) khi \(\left( P \right):{y_A} = a{x_A}^2\left( {a \ne 0} \right)\) Cách giải: Đồ thị hàm số \(y = \left( {m - 2} \right){x^2}\) đi qua điểm \(A\left( {1;2} \right)\) khi \(\left( {m - 2} \right){.1^2} = 2 \Leftrightarrow m = 4\) Chọn C. Câu 6 Phương pháp: Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0\) (hoặc \(\Delta ' > 0\)) Cách giải: Ta có: \(\Delta ' = {\left( { - 1} \right)^2} - m = 1 - m\) Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\) \(\begin{array}{l} \Leftrightarrow 1 - m > 0\\ \Leftrightarrow m < 1\end{array}\) Vậy \(m < 1\) Chọn D. Câu 7 Phương pháp: Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) vô nghiệm \( \Leftrightarrow \Delta < 0\) (hoặc \(\Delta ' < 0\)) Cách giải: Xét phương trình: \({x^2} + x + 1 = 0\) Ta có: \(\Delta = 1 - 4.1 = - 3 < 0\) \( \Rightarrow \) Phương trình vô nghiệm. Chọn A. Câu 8 Phương pháp: Áp dụng hệ thức lượng trong tam giác vuông. Cách giải:
\(\Delta ABC\) vuông tại \(A\), đường cao \(AH\), áp dụng hệ thức lượng trong tam giác vuông, ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\,A{C^2} = CH.CB\\ \Rightarrow BC = \dfrac{{A{C^2}}}{{CH}} = \dfrac{{{5^2}}}{4} = \dfrac{{25}}{4}\left( {cm} \right)\end{array}\) Chọn B. Câu 9 Phương pháp: Vận dụng kiến thức về đường kính và dây cung Áp dụng định lý Py – ta – go Cách giải:
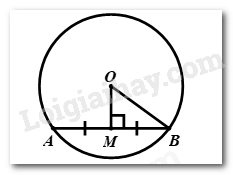
Xét đường tròn \(\left( O \right)\)kẻ \(OM \bot AB\) tại \(M\) \( \Rightarrow M\) là trung điểm của \(AB\) (quan hệ đường kính và dây cung trong đường tròn) \( \Rightarrow BM = \dfrac{1}{2}AB = 12\left( {cm} \right)\) \(\begin{array}{l}\,\,\,\,\,\,\,\,\,O{B^2} = O{M^2} + M{B^2}\\ \Leftrightarrow O{M^2} = O{B^2} - M{B^2}\\ \Leftrightarrow O{M^2} = {13^2} - {12^2}\\ \Leftrightarrow O{M^2} = 25\\ \Rightarrow OM = 5\left( {cm} \right)\end{array}\) Vậy khoảng cách từ \(O\) đến dây \(AB\) là \(5\left( {cm} \right)\) Chọn C. Câu 10 Phương pháp: Sử dụng tính chất góc của tứ giác nội tiếp Vận dụng định lý tổng ba góc trong một tam giác. Cách giải: Tứ giác \(MNPQ\) nội tiếp đường tròn \( \Rightarrow \angle MNP + \angle MQP = {180^0}\) (tính chất của tứ giác nội tiếp) \(\begin{array}{l} \Leftrightarrow {60^0} + \angle MQP = {180^0}\\ \Leftrightarrow \angle MQP = {120^0}\end{array}\) Xét \(\Delta MPQ\) có: \(\angle QMP + \angle MPQ + \angle PQM = {180^0}\) (định lý tổng ba góc trong một tam giác) \(\begin{array}{l} \Leftrightarrow {40^0} + \angle MPQ + {120^0} = {180^0}\\ \Leftrightarrow \angle MPQ = {20^0}\end{array}\) Chọn B. PHẦN II. TỰ LUẬN Bài 1 Phương pháp: a) Kiểm tra \(x = 16\) có TMĐK xác định Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\) Thực hiện các phép tính với căn bậc hai. b) Xác định mẫu thức chung của biểu thức Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức. Cách giải: a) Thay \(x = 16\)(TMĐK) vào biểu thức ta được \(\begin{array}{l}A = \dfrac{{ - 7\sqrt {16} + 6}}{{16 - 4}} + \dfrac{{\sqrt {16} }}{{\sqrt {16} - 2}}\\A = \dfrac{{ - 28 + 6}}{{12}} + \dfrac{4}{{4 - 2}}\\A = \dfrac{{ - 11}}{6} + 2\\A = \dfrac{1}{6}\end{array}\) Vậy với \(x = 16\) thì \(A = \dfrac{1}{6}\) b) Với \(x \ge 0,\,x \ne 4\) có \(A = \dfrac{{ - 7\sqrt x + 6}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{{\sqrt x }}{{\sqrt x - 2}}\) \(A = \dfrac{{ - 7\sqrt x + 6}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\) \(A = \dfrac{{ - 7\sqrt x + 6 + x + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\) \(A = \dfrac{{x - 5\sqrt x + 6}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\) \(A = \dfrac{{x - 2\sqrt x - 3\sqrt x + 6}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\) \(A = \dfrac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\) \(A = \dfrac{{\sqrt x - 3}}{{\sqrt x + 2}}\) Vậy \(A = \dfrac{{\sqrt x - 3}}{{\sqrt x + 2}}\) Bài 2 Phương pháp: 1) a) Đường thẳng \(\left( d \right):y = ax + b\) đi qua điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) khi \({y_A} = a{x_A} + b\) b) Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) (phương trình \(\left( * \right)\)) Đường thẳng \(\left( d \right)\) tiếp xúc với Parabol \(\left( P \right)\)\( \Leftrightarrow \left( * \right)\) có nghiệm kép \( \Leftrightarrow \Delta = 0\) (hoặc \(\Delta ' = 0\)) 2) a) Thay \(m = 2\) vào hệ phương trình Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\) Sử dụng phương pháp thế, tìm được nghiệm \(y\) Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình. b) Từ hệ phương trình ban đầu, tìm nghiệm \(x,y\) theo tham số \(m\) Thay vào phương trình của đề bài, tìm được \(m\). Cách giải: 1) a) Tìm m để đường thẳng \(\left( d \right):y = 2mx + 2m - 3\) đi qua \(A\left( {1;5} \right).\) Do (d) đi qua \(A\left( {1;5} \right).\) Thay \(x = 1;\,\,y = 5\)vào phương trình đường thẳng ta được: \(5 = 2m.1 + 2m - 3 \Leftrightarrow 4m = 8 \Leftrightarrow m = 2\) Vậy với m = 2 thì đường thẳng \(\left( d \right):y = 2mx + 2m - 3\) đi qua \(A\left( {1;5} \right).\) b) Tìm m để đường thẳng \(\left( d \right)\) tiếp xúc với Parabol \(\left( P \right)\) Phương trình hoành độ giao điểm của (d) và (P) là \({x^2} = 2mx + 2m - 3 \Leftrightarrow {x^2} - 2mx - 2m + 3 = 0\left( * \right)\) \({\Delta ^'} = {\left( { - m} \right)^2} - \left( { - 2m + 3} \right) = {m^2} + 2m - 3\) Để \(\left( d \right)\) tiếp xúc với Parabol \(\left( P \right)\) thì phương trình (*) có nghiệm kép hay \(\Delta ' = 0 \Leftrightarrow {m^2} + 2m - 3 = 0 \Leftrightarrow \left( {m - 1} \right)\left( {m + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 3\end{array} \right.\) Vậy \(m = 1\) hoặc \(m = - 3\) 2) a) Thay \(m = 2\) vào phương trình ta được \(\left\{ \begin{array}{l}2x - y = 2 - 1\\3x + y = 4.2 + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = 1\\3x + y = 9\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2x - y = 1\\3x + y = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\2x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2.2 - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\) Vậy với \(m = 2\) hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2;3} \right)\) b) Ta thấy \(\dfrac{2}{3} \ne \dfrac{{ - 1}}{1}\) nên hệ phương trình có nghiệm duy nhất với \(\forall m\) \(\left\{ \begin{array}{l}2x - y = m - 1\\3x + y = 4m + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 5m\\3x + y = 4m + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = m\\3m + y = 4m + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = m\\y = m + 1\end{array} \right.\) Thay vào phương trình \(2{x^2} - 3y = 2\) ta được: \(\begin{array}{l}2{m^2} - 3\left( {m + 1} \right) = 2 \Leftrightarrow 2{m^2} - 3m - 5 = 0 \Leftrightarrow \left( {2m - 5} \right)\left( {m + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = \dfrac{5}{2}\end{array} \right.\end{array}\) Vậy \(m \in \left\{ { - 1;\,\,\dfrac{5}{2}} \right\}\) Bài 3 Phương pháp: a) Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp. b) Ta sẽ chứng minh: + Tứ giác \(AHKE\) nội tiếp \( \Rightarrow \angle EHK = \angle EAK\) + \(\angle EAK = \angle KBA\) (cùng phụ với \(\angle KAB\)) \( \Rightarrow \angle EHK = \angle KBA\) c) Ta sẽ chứng minh: \(\angle MOE = \angle AEO;\angle AEO = \angle MEO \Rightarrow \)\(\angle MOE = \angle MEO\)\( \Rightarrow \Delta MEO\) cân tại \(M\)\( \Rightarrow ME = MO\) Áp dụng hệ quả của định lý Ta – lét Cách giải:
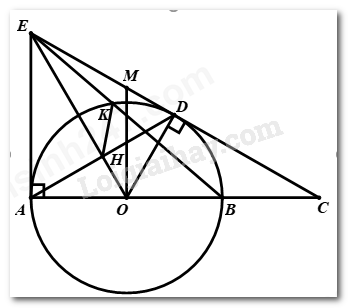
a) Xét đường tròn \(\left( O \right)\) có: + \(EA\) là tiếp tuyến của đường tròn \( \Rightarrow \angle EAB = {90^0}\) + \(ED\) là tiếp tuyến của đường tròn \( \Rightarrow \angle ODE = {90^0}\) Tứ giác \(AODE\) có: \(\angle EAB + \angle ODE = {90^0} + {90^0} = {180^0}\) \( \Rightarrow AODE\) là tứ giác nội tiếp đường tròn (dấu hiệu nhận biết) b) Xét đường tròn \(\left( O \right)\) có: \(EA,ED\) là hai tiếp tuyến của đường tròn Mà \(EA \cap ED = \left\{ E \right\}\) \( \Rightarrow EA = ED\) (tính chất hai tiếp tuyến cắt nhau) Lại có: \(OA = OD = R\) \( \Rightarrow EO\) là đường trung trực của \(AD\) \(\begin{array}{l} \Rightarrow EO \bot AD\\ \Rightarrow \angle EHA = {90^0}\end{array}\) Ta có: \(\angle AKB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle EKA = {90^0}\) (kề bù với \(\angle AKB\)) Xét tứ giác \(AHKE\) có: \(\angle EKA = \angle EHA = {90^0}\) Mà \(K,H\) là hai đỉnh kề nhau \( \Rightarrow AHKE\) là tứ giác nội tiếp \( \Rightarrow \angle EHK = \angle EAK\) (hai góc nội tiếp cùng chắn \(cungEK\)) Mà \(\angle EAK = \angle KBA\) (cùng phụ với \(\angle KAB\)) \( \Rightarrow \angle EHK = \angle KBA\) c) Ta có: \(\left\{ \begin{array}{l}OM \bot AB\left( {gt} \right)\\EA \bot AB\left( {cmt} \right)\end{array} \right. \Rightarrow OM//EA\) (quan hệ từ vuông góc đến dây cung) \( \Rightarrow \angle MOE = \angle AEO\) (hai góc so le trong) (1) Xét đường tròn \(\left( O \right)\) có: \(EA,ED\) là hai tiếp tuyến của đường tròn Mà \(EA \cap ED = \left\{ D \right\}\) \( \Rightarrow \angle AEO = \angle DEO\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow \angle AEO = \angle MEO\) (2) Từ (1) và (2), suy ra \(\angle MOE = \angle MEO\)\( \Rightarrow \Delta MEO\) cân tại \(M \Rightarrow ME = MO\) \(\Delta CAE\) có \(OM//EA\left( {cmt} \right)\), áp dụng hệ quả của định lí Ta – lét, ta có: \(\dfrac{{OM}}{{AE}} = \dfrac{{MC}}{{CE}} \Rightarrow \dfrac{{EA}}{{OM}} = \dfrac{{CE}}{{MC}} \Rightarrow \dfrac{{EA}}{{EM}} = \dfrac{{MC + EM}}{{MC}}\) \( \Rightarrow \dfrac{{EA}}{{EM}} = 1 + \dfrac{{EM}}{{MC}} \Rightarrow \dfrac{{EA}}{{EM}} - \dfrac{{MO}}{{MC}} = 1\) (vì \(ME = MO\)) Bài 4 Phương pháp: Xuất phát từ bất đẳng thức: \(2bc \le {b^2} + {c^2}\) Cách giải: Ta có: \(2bc \le {b^2} + {c^2}\) Khi đó, \(A \le \left( {1 + 2a} \right)\left( {1 + {b^2} + {c^2}} \right) = \left( {1 + 2a} \right)\left( {2 - {a^2}} \right)\) (vì \({a^2} + {b^2} + {c^2} = 1\)) Có \(\left( {1 + 2a} \right)\left( {2 - {a^2}} \right) = \dfrac{1}{{54}}\left( {6 + 12a} \right)\left( {18 - 9{a^2}} \right) \le \dfrac{1}{{54}}\left( {10 + 9{a^2}} \right)\left( {18 - 9{a^2}} \right)\) \( \le \dfrac{1}{{54}}{\left( {\dfrac{{10 + 9{a^2} + 18 - 9{a^2}}}{2}} \right)^2} = \dfrac{{98}}{{27}}\,\,\,\,\,\left( {do\,9{a^2} + 4 \ge 12a} \right)\) Do đó \(A \le \dfrac{{98}}{{27}}\) Dấu “=” xảy ra khi: \(\left\{ \begin{array}{l}a = \dfrac{2}{3}\\b = c\\{a^2} + {b^2} + {c^2} = 1\\10 + 9{a^2} = 18 - 9{a^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{2}{3}\\b = c = \dfrac{{\sqrt {10} }}{6}\end{array} \right.\) Vậy \(MaxA = \dfrac{{98}}{{27}}\) khi \(a = \dfrac{2}{3};\,\,b = c = \dfrac{{\sqrt {10} }}{6}\)
|














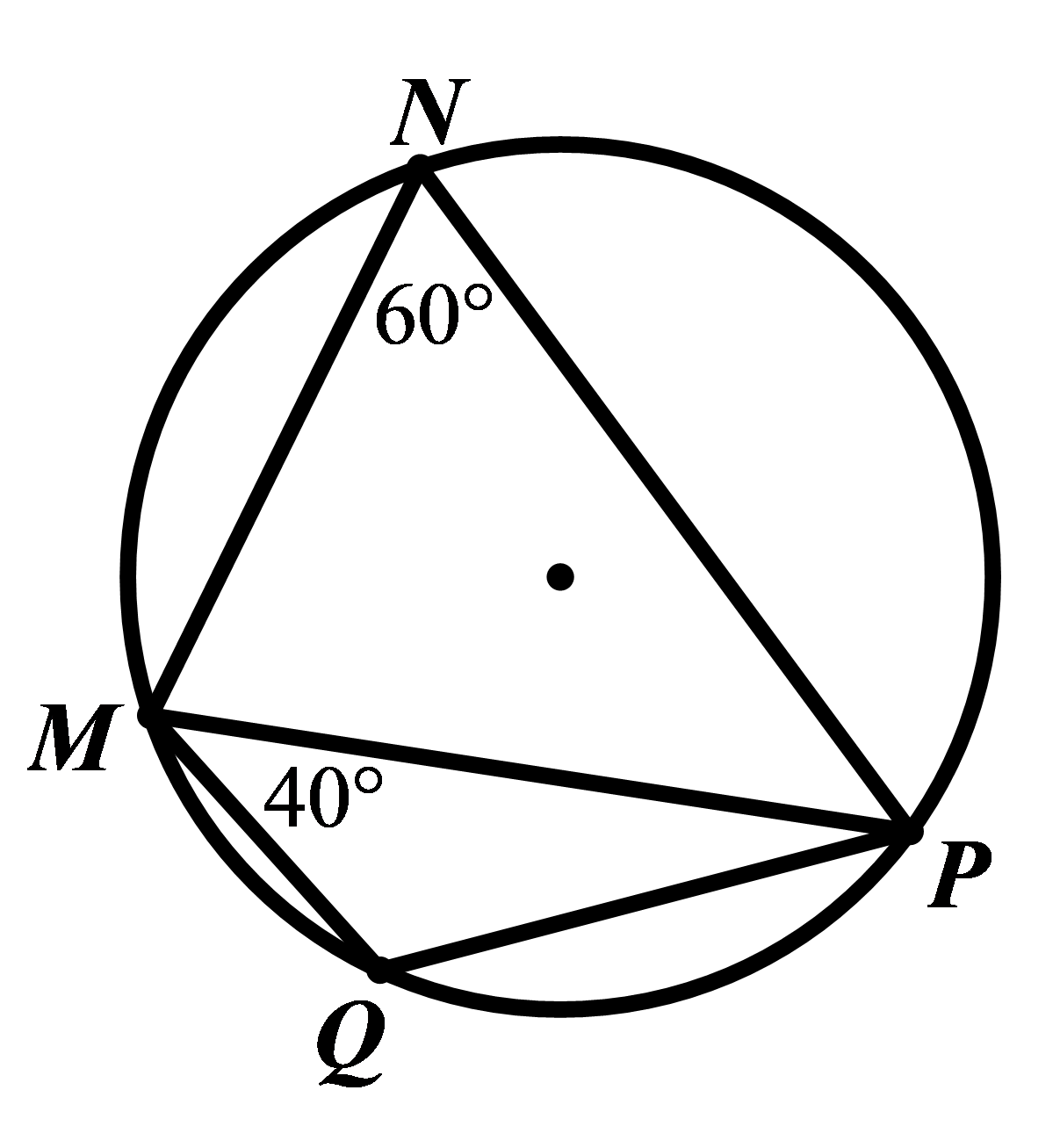






Danh sách bình luận