Đề thi vào 10 môn Toán TP Hồ Chí Minh năm 2018

Đề bài

Bài 1 (1,5 điểm) Cho parabol \(\left( P \right):\;\;y = {x^2}\) và đường thẳng \(\left( d \right):\;\;y = 3x - 2.\)

a) Vẽ \(\left( P \right)\)  và \(\left( d \right)\) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.

Bài 2 (1 điểm). Cho phương trình \(3{x^2} - x - 1 = 0\)  có \(2\) nghiệm là \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị của biểu thức \(A = x_1^2 + x_2^2\).

Bài 3 (1 điểm). Mối quan hệ giữa thang nhiệt độ F (Fahrenheit) và thang nhiệt độ C (Celsius) được cho bởi công thức \({T_F} = 1,8.{T_C} + 32,\) trong đó \({T_C}\) là nhiệt độ tính theo độ C và \({T_F}\) là nhiệt độ tính theo độ F. Ví dụ \({T_C} = {0^0}\) C tương ứng với \({T_F} = {32^0}\) F.

a) Hỏi \({25^0}\) C tương ứng với bao nhiêu độ F ?

b) Các nhà khoa học đã tìm ra mối liên hệ giữa \(A\) là số tiếng kêu của một con dế trong một phút và \({T_F}\) là nhiệt độ cơ thể của nó bởi công thức \(A = 5,6.{T_F} - 275,\) trong đó \({T_F}\) là nhiệt độ tín theo độ F. Hỏi nếu con dế kêu 106 tiếng trong một phút thì nhiệt độ của nó khoảng bao nhiêu độ C? (làm tròn đến hàng đơn vị)

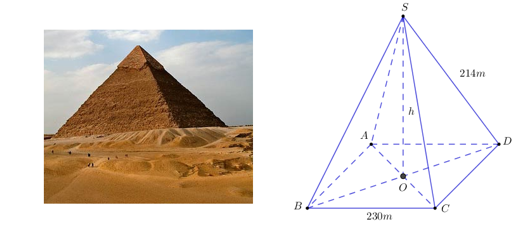
Bài  (0,75 điểm) Kim tự tháp Kheops – Ai Cập có dạng hình chóp đều, đáy là hình vuông, các mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của kim tự tháp dài 214 m, cạnh đáy của nó dài 230 m.

a) Tính theo mét chiều cao h của kim tự tháp (làm tròn đến chữ số thập phân thứ nhất).

b) Cho biết thể tích của hình chóp được tính theo công thức \(V = \dfrac{1}{3}Sh\), trong đó \(S\) là diện tích mặt đáy, h là chiều cao của hình chóp. Tính theo \({m^3}\) thể tích của kim tự tháp (làm tròn đến hàng nghìn).

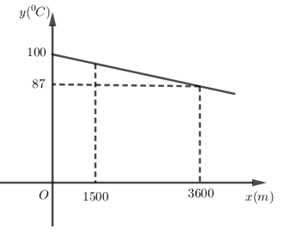
Bài 5 (1 điểm). Siêu thị A thực hiện chương trình giảm giá cho khách hàng mua loại túi bột giặt 4 kg như sau: Nếu mua 1 túi thì được giảm giá 10 000 đồng so với giá niêm yết. Nếu mua 2 túi thì túi thứ nhất được giảm 10 000 đồng và túi thứ hai được giảm 20 000 đồng so với giá niêm yết. Nếu mua từ 3 túi trở lên thì ngoài 2 túi đầu được hưởng chương trình giảm giá như trên, từ túi thứ ba trở đi mỗi túi sẽ được giảm 20% so với giá niêm yết.

a) Bà Tư mua 5 túi bột giặt loại 4 kg ở siêu thị A thì phải trả số tiền là bao nhiêu, biết rằng loại túi bột giặt mà bà Tư mua có giá niêm yết là 150 000 đồng/túi.

b) Siêu thị B lại có hình thức giảm giá khác cho loại túi bột giặt nêu trên là: nếu mua từ 3 túi trở lên thì sẽ giảm giá 15% cho mỗi túi. Nếu bà Tư mua 5 túi bột giặt thì bà Tư nên mua ở siêu thị nào để số tiền phải trả ít hơn? Biết rằng giá niêm yết của hai siêu thị là như nhau.

Bài 6 (1 điểm). Nhiệt độ sôi của nước không phải lúc nào cũng là \({100^0}C\) mà phụ thuộc vào độ cao của nơi đó so với mực nước biển. Chẳng hạn Thành phố Hồ Chí Minh có độ cao xem như ngang mực nước biển \(\left( {x = 0\,m} \right)\) thì nước có nhiệt độ sôi là \(y = {100^0}C\) nhưng ở thủ đô La Paz của Bolivia, Nam Mỹ có độ cao \(x = 3\,600\,m\) so với mực nước biển thì nhiệt độ sôi của nước là \(y = {87^0}C\). Ở độ cao trong khoảng vài \(km\), người ta thấy mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất \(y = ax + b\) có đồ thị như sau:

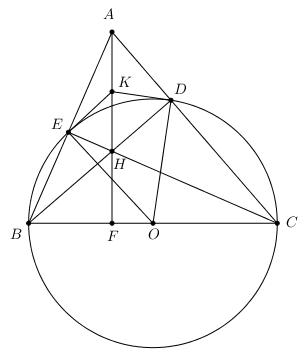
Bài 7(1 điểm) Năm học 2017 – 2018, trường THCS Tiến Thành có ba lớp 9 gồm 9A, 9B, 9C trong đó lớp 9A có 35 học sinh và lớp 9B có 40 học sinh. Tổng kết cuối năm, lớp 9A có 15 học sinh đạt danh hiệu học sinh giỏi, lớp 9B có 12 học sinh đạt danh hiệu học sinh giỏi, lớp 9C có 20% học sinh đạt danh hiệu học sinh giỏi và toàn khối 9 có 30% học sinh đạt danh hiệu học sinh giỏi. Hỏi lớp 9C có bao nhiêu học sinh?

Bài 8 (3 điểm).  Cho tam giác nhọn ABC có BC = 8 cm. Đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và D. Hai đường thẳng BD và CE cắt nhau tại H.

a) Chứng minh: AH vuông góc với BC.

b) Gọi K là trung điểm của AH. Chứng minh tứ giác OEKD nội tiếp.

c) Cho \(\widehat {BAC} = {60^0}\). Tính độ dài đoạn DE và tỉ số diện tích của hai tam giác AED và ABC.

Lời giải chi tiết

Bài 1 (1,5 điểm)

Cho parabol \(\left( P \right):\;\;y = {x^2}\) và đường thẳng \(\left( d \right):\;\;y = 3x - 2.\)

Phương pháp:

a) Lập bảng giá trị các điểm thuộc đồ thị hàm số sau đó vẽ đồ thị hàm số trên trục tọa độ.

b) Giải phương trình hoành độ giao điểm của hai đồ thị để tìm hoành độ giao điểm từ đó tìm tung độ giao điểm của hai đồ thị.

Cách giải:

a) Vẽ \(\left( P \right)\)  và \(\left( d \right)\) trên cùng hệ trục tọa độ.

+) Vẽ đồ thị hàm số \(\left( P \right):\;\;y = {x^2}:\)

 Ta có bảng giá trị:

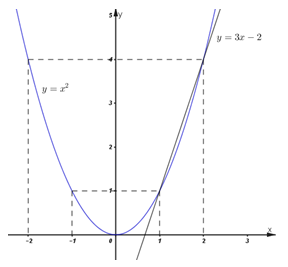
Đồ thị hàm số (P) có hình dạng đường cong đi qua các điểm \(\left( {0;\;0} \right),\;\;\left( { - 1;\;1} \right),\;\;\left( { - 2;\;4} \right),\;\;\left( {1;\;1} \right),\;\left( {2;\;4} \right).\)

+) Vẽ đồ thị hàm số: \(\left( d \right):\;\;y = 3x - 2.\)

Đồ thị hàm số \(\left( d \right):\;\;y = 3x - 2\) là đường thẳng đi qua các điểm \(\left( {1;\;1} \right),\;\;\left( {2;\;\;4} \right).\)

Đồ thị hàm số:

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.

Hoành độ giao điểm của \(\left( d \right)\)  và \(\left( P \right)\) là nghiệm của phương trình:

\(\begin{array}{l}{x^2} = 3x - 2 \Leftrightarrow {x^2} - 3x + 2 = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = 1\\x = 2 \Rightarrow y = 4\end{array} \right..\end{array}\)

Vậy đường thẳng \(\left( d \right)\)  cắt \(\left( P \right)\) tại hai điểm phân biệt: \(\left( {1;\;1} \right)\) và \(\left( {2;\;\;4} \right).\)

Bài 2 (1 điểm).

Cho phương trình \(3{x^2} - x - 1 = 0\)  có \(2\) nghiệm là \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị của biểu thức \(A = x_1^2 + x_2^2\).

Phương pháp:

Áp dụng hệ thức Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right..\)

Cách giải:

Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a} = \dfrac{1}{3}\\{x_1}{x_2} = \dfrac{c}{a} =  - \dfrac{1}{3}\end{array} \right.\)

\( \Rightarrow A = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {\left( {\dfrac{1}{3}} \right)^2} - 2.\left( { - \dfrac{1}{3}} \right) = \dfrac{1}{9} + \dfrac{2}{3} = \dfrac{7}{9}\).

Vậy \(A = \dfrac{7}{9}\).

Bài 3 (1 điểm):

Mối quan hệ giữa thang nhiệt độ F (Fahrenheit) và thang nhiệt độ C (Celsius) được cho bởi công thức \({T_F} = 1,8.{T_C} + 32,\) trong đó \({T_C}\) là nhiệt độ tính theo độ C và \({T_F}\) là nhiệt độ tính theo độ F. Ví dụ \({T_C} = {0^0}\) C tương ứng với \({T_F} = {32^0}\) F.

Phương pháp:

+) Thay nhiệt độ có đơn vị độ C vào công thức để tìm độ F.

Cách giải:

a) Hỏi \({25^0}\) C tương ứng với bao nhiêu độ F ?

Với \({T_C} = {25^0}\) C thay vào biểu thức \({T_F} = 1,8.{T_C} + 32,\) ta được \({T_F} = 1,8.25 + 32 = {77^0}\) F.

Vậy \({25^0}\) C tương ứng với 77 độ F.

b) Các nhà khoa học đã tìm ra mối liên hệ giữa \(A\) là số tiếng kêu của một con dế trong một phút và \({T_F}\) là nhiệt độ cơ thể của nó bởi công thức \(A = 5,6.{T_F} - 275,\) trong đó \({T_F}\) là nhiệt độ tín theo độ F. Hỏi nếu con dế kêu 106 tiếng trong một phút thì nhiệt độ của nó khoảng bao nhiêu độ C? (làm tròn đến hàng đơn vị)

Con dế kêu 106 tiếng trong một phút suy ra \(106 = 5,6.{T_F} - 275 \Leftrightarrow 5,6.{T_F} = 381 \Leftrightarrow {T_F} = \dfrac{{1905}}{{28}}.\)

Mà \({T_F} = 1,8.{T_C} + 32\) suy ra \({T_C} = \dfrac{{{T_F} - 32}}{{1,8}} = \dfrac{{\dfrac{{1905}}{{28}} - 32}}{{1,8}}\,\, \approx \,\,{20^0}\) C (làm tròn đến hàng đơn vị)

Vậy khi con dế kêu 106 tiếng trong một phút thì nhiệt độ của nó khoảng 20 độ C.

Bài 4:

Phương pháp:

+) Áp dụng định lý Pi-ta-go và công thức tính thể tích của khối chóp: \(V = \dfrac{1}{3}{S_d}.h.\)

Cách giải:

a)      Chứng minh AH vuông góc với BC

 Ta có các góc \(BDC = {90^0};\,BEC\, = {90^0}\)

(Góc nội tiếp chắn nửa đường tròn)

\(\begin{array}{l} \Rightarrow BD \bot DC \Rightarrow BD \bot AC\\\,\,\,\,\,\,\,CE \bot BE \Rightarrow CE \bot AB\end{array}\)

Xét tam giác ABC có \(\left\{ \begin{array}{l}BD \bot AC\\CE \bot AC\\BD \cap CE = H\,\,\left( {gt} \right)\end{array} \right. \Rightarrow \) H là trực tâm tam giác ABC

\( \Rightarrow AH \bot BC\).

b) Gọi K là trung điểm của AH. Chứng minh tứ giác OEKD nội tiếp

Kéo dài AH cắt BC tại F.

Xét tứ giác AEHD có \(\angle AEH + \angle ADH = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác AEDH nội tiếp đường tròn đường kính AH.

Lại có K là trung điểm của AH \( \Rightarrow K\) là tâm đường tròn ngoại tiếp tứ giác AEHD.

\( \Rightarrow KA = KE = KH = KD\)

\( \Rightarrow \Delta KDH\) cân tại K \( \Rightarrow \angle KDH = \angle KHD = \angle BHF\) (1)

Xét tam giác OBD có \(OB = OD\,\left( { = R} \right) \Rightarrow \Delta OBD\) cân tại O \( \Rightarrow \angle ODB = \angle OBD\)  (2)

Từ (1) và (2) \( \Rightarrow \angle KDH + \angle ODB = \angle BHF + \angle OBD = {90^0} \Rightarrow \angle KDO = {90^0}\)

Chứng minh tương tự ta có:

\(\Delta KEH\) cân tại K \( \Rightarrow \angle KEH = \angle KHE = \angle CHF\)

Tam giác OCE có OC = OE \( \Rightarrow \Delta OCE\) cân tại \(O \Rightarrow \angle OEC = \angle OCE\)

\( \Rightarrow \angle KEH + \angle OEC = \angle CHF + \angle OCE = {90^0} \Rightarrow \angle KEO = {90^0}\)

Xét tứ giác OEKD có \(\angle KDO + \angle KEO = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác OEKD là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰)

 c) Cho \(\angle BAC = {60^0}\). Tính độ dài đoạn DE và tỉ số diện tích hai tam giác AED và ABC.

 Tứ giác BEDC nội tiếp đường tròn (O)

\( \Rightarrow \angle ABC + \angle EDC = {180^0}\)

Mà \(\angle EDC + \angle ADE = {180^0}\) (kề bù)

\( \Rightarrow \angle ABC = \angle ADE\)

+) Xét \(\Delta ADE\) và \(\Delta ABC\)có:

\(\angle A\) : chung

 \(\angle ABC = \angle ADE\) (cmt)

\( \Rightarrow \Delta ADE\) đồng dạng \(\Delta ABC\) (g-g)

\( \Rightarrow \dfrac{{DE}}{{BC}} = \dfrac{{AD}}{{AB}}\) (1)

+) \(\Delta ADB\)vuông tại D

 \( \Rightarrow \dfrac{{AD}}{{AB}} = {\mathop{\rm cosBAD}\nolimits}  = \cos {60^0} = \dfrac{1}{2}\) (2)

 Từ (1), (2) suy ra : \(\dfrac{{DE}}{{BC}} = \dfrac{1}{2} \Rightarrow DE = \dfrac{1}{2}BC = \dfrac{1}{2}.8 = 4\,\,(cm)\)

Vậy \(DE = 4\,\,cm\).

+) \(\Delta ADE\) đồng dạng \(\Delta ABC\) với tỉ số đồng dạng \(k = \dfrac{{DE}}{{BC}} = \dfrac{1}{2}\)

Khi đó: \(\dfrac{{{S_{\Delta ADE}}}}{{{S_{\Delta ABC}}}} = {k^2} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}\).