Đề thi vào 10 môn Toán An Giang năm 2020

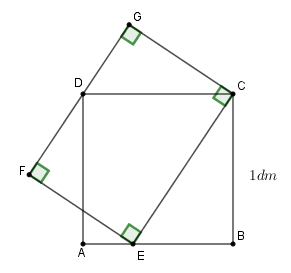
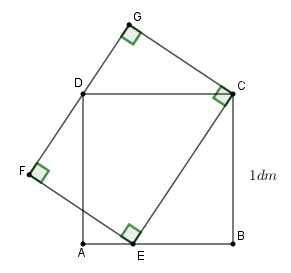
Đề bài

Câu 1:  Giải các phương trình và hệ phương trình sau đây:

a.\(\sqrt 3 x - \sqrt 3  = \sqrt 3 \)                                           b. \(\left\{ \begin{array}{l}x + y = 7\\ - x + 2y = 2\end{array} \right.\)                                    c. \({x^4} - 3{x^2} - 4 = 0\)

Câu 2:  Cho hàm số \(y = {x^2}\) có đồ thị là parabol \(\left( P \right).\)

a. Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ

b. Viết phương trình đường thẳng \(\left( d \right)\) có hệ số góc bằng \( - 1\) và cắt parabol \(\left( P \right)\) tại điểm có hoành độ bằng \(1.\)

c. Với \(\left( d \right)\) vừa tìm được, tìm tọa độ giao điểm còn lại của \(\left( d \right)\) và \(\left( P \right)\)

Câu 3:  

Cho phương trình bậc hai \({x^2} - 2x + m - 1 = 0\) (*), với \(m\) là tham số

a. Tìm tất cả các giá trị của \(m\) để phương trình (*) có nghiệm

b. Tính theo \(m\) giá trị của biểu thức \(A = x_1^3 + x_2^3\) với \({x_1},{x_2}\) là hai nghiệm của phương trình (*). Tìm giá trị nhỏ nhất của \(A.\)

Câu 4:  Cho tam giác ABC có ba góc đều nhọn và nội tiếp trong đường tròn (O). Vẽ các đường cao AA’, BB’, CC’ cắt nhau tại H.

a) Chứng minh rằng tứ giác AB’HC’ là tứ giác nội tiếp.

b) Kéo dài AA’ cắt đường tròn (O) tại điểm D. Chứng minh rằng tam giác CDH cân.

Câu 5:  Cho \(ABCD\) là hình vuông có cạnh \(1dm.\) Trên cạnh \(AB\) lấy một điểm \(E.\) Dựng hình chữ nhật \(CEFG\) sao cho điểm \(D\) nằm trên cạnh \(FG.\) Tính diện tích hình chữ nhật \(CEFG\) (hình vẽ bên).

Lời giải chi tiết

Câu 1 (3,0 điểm)

Cách giải:

Giải các phương trình và hệ phương trình sau đây:

a.\(\sqrt 3 x - \sqrt 3  = \sqrt 3 \)

Ta có: \(\sqrt 3 x - \sqrt 3  = \sqrt 3 \)

\(\begin{array}{l} \Leftrightarrow \sqrt 3 x = \sqrt 3  + \sqrt 3 \\ \Leftrightarrow \sqrt 3 x = 2\sqrt 3 \\ \Leftrightarrow x = 2\sqrt 3 :\sqrt 3 \\ \Leftrightarrow x = 2\end{array}\)

Vậy phương trình có nghiệm \(x = 2.\)

b. \(\left\{ \begin{array}{l}x + y = 7\\ - x + 2y = 2\end{array} \right.\)

Ta có:

\(\left\{ \begin{array}{l}x + y = 7\\ - x + 2y = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3y = 9\\x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x + 3 = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x = 4\end{array} \right.\)

Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {4;3} \right)\)

c. \({x^4} - 3{x^2} - 4 = 0\)

Ta có:

\(\begin{array}{l}{x^4} - 3{x^2} - 4 = 0\\ \Leftrightarrow {x^4} - 4{x^2} + {x^2} - 4 = 0\\ \Leftrightarrow {x^2}\left( {{x^2} - 4} \right) + \left( {{x^2} - 4} \right) = 0\\ \Leftrightarrow \left( {{x^2} + 1} \right)\left( {{x^2} - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} + 1 = 0\\{x^2} - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} =  - 1\left( {VN} \right)\\{x^2} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x =  - 2\end{array} \right.\end{array}\)

Vậy phương trình có nghiệm \(x =  - 2;x = 2.\)

Câu 2 (2 điểm)

Cách giải:

Cho hàm số \(y = {x^2}\) có đồ thị là parabol \(\left( P \right).\)

a. Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ

Bảng giá trị:

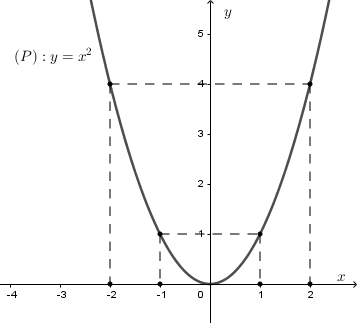
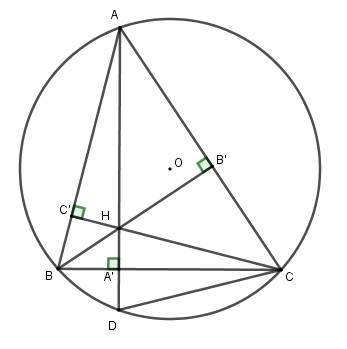
Đồ thị hàm số \(y = {x^2}\) là parabol \(\left( P \right)\) đi qua các điểm \(\left( { - 2;4} \right),\left( { - 1;1} \right),\left( {0;0} \right),\left( {1;1} \right),\left( {2;4} \right)\)

Hình vẽ:

b. Viết phương trình đường thẳng \(\left( d \right)\) có hệ số góc bằng \( - 1\) và cắt parabol \(\left( P \right)\) tại điểm có hoành độ bằng \(1.\)

Gọi phương trình đường thẳng \(\left( d \right):y = ax + b\)

Vì đường thẳng \(\left( d \right)\) có hệ số góc bằng \( - 1\) nên \(a =  - 1\)

Suy ra \(\left( d \right):y =  - x + b\)

Gọi giao điểm của \(\left( d \right)\) và parabol \(\left( P \right)\) là \(M\left( {1;y} \right)\)

Vì \(M\left( {1;y} \right) \in \left( P \right)\) nên \(y = {x^2} = {1^2} = 1\), suy ra \(M\left( {1;1} \right)\)

Lại có \(M\left( {1;1} \right) \in \left( d \right)\) nên \(1 =  - 1 + b \Leftrightarrow b = 2\)

Vậy phương trình đường thẳng \(\left( d \right):y =  - x + 2\).

c. Với \(\left( d \right)\) vừa tìm được, tìm tọa độ giao điểm còn lại của \(\left( d \right)\) và \(\left( P \right)\)

Theo câu b) ta có: \(\left( d \right):y =  - x + 2\)

Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\), ta được:

\(\begin{array}{l}{x^2} =  - x + 2\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} - x + 2x - 2 = 0\\ \Leftrightarrow x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 2\\x = 1\end{array} \right.\end{array}\)

Với \(x = 1 \Rightarrow y = {1^2} = 1\)

Với \(x =  - 2 \Rightarrow y = {\left( { - 2} \right)^2} = 4\)

Vậy tọa độ giao điểm còn lại của \(\left( d \right)\) và \(\left( P \right)\) là: \(\left( { - 2;4} \right)\)

Câu 3 (2 điểm)

Cách giải:

Cho phương trình bậc hai \({x^2} - 2x + m - 1 = 0\) (*), với \(m\) là tham số

a. Tìm tất cả các giá trị của \(m\) để phương trình (*) có nghiệm

Xét phương trình \({x^2} - 2x + m - 1 = 0\) (*) có:

\(\Delta ' = {\left( { - 1} \right)^2} - 1.\left( {m - 1} \right) = 2 - m\)

Để phương trình (*) có nghiệm thì \(\left\{ \begin{array}{l}a \ne 0\\\Delta ' \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\left( {ld} \right)\\2 - m \ge 0\end{array} \right. \Leftrightarrow m \le 2\)

Vậy với \(m \le 2\) thì phương trình (*) có nghiệm

b. Tính theo \(m\) giá trị của biểu thức \(A = x_1^3 + x_2^3\) với \({x_1},{x_2}\) là hai nghiệm của phương trình (*). Tìm giá trị nhỏ nhất của \(A.\)

Theo câu a) với \(m \le 2\) thì phương trình (*) có nghiệm \({x_1},{x_2}\)

Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m - 1\end{array} \right.\)

Xét \(A = x_1^3 + x_2^3\)

\(\begin{array}{l} = x_1^3 + 3x_1^2{x_2} + 3{x_1}x_2^2 + x_2^3 - \left( {3x_1^2{x_2} + 3{x_1}x_2^2} \right)\\ = {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)\\ = {2^3} - 3\left( {m - 1} \right).2\\ = 8 - 6\left( {m - 1} \right)\\ = 8 - 6m + 6\\ = 14 - 6m\end{array}\)

Vậy \(A = 14 - 6m\)

Vì \(m \le 2\) nên ta có: \(6m \le 12 \Leftrightarrow 14 - 6m \ge 14 - 12 \Leftrightarrow 14 - 6m \ge 2\)

Dấu “=” xảy ra khi \(m = 2\)

Vậy giá trị nhỏ nhất của A là \(2 \Leftrightarrow m = 2\).

Câu 4 (2,0 điểm)

Cách giải:

Cho tam giác ABC có ba góc đều nhọn và nội tiếp trong đường tròn (O). Vẽ các đường cao AA’, BB’, CC’ cắt nhau tại H.

a) Chứng minh rằng tứ giác AB’HC’ là tứ giác nội tiếp.

Ta có:

\(\begin{array}{l}BB' \bot AC \Rightarrow \angle AB'H = {90^0}\\CC' \bot AB \Rightarrow \angle AC'H = {90^0}\end{array}\)

Tứ giác AB’HC’ có:

\(\angle AB'H + \angle AC'H = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)) (đpcm)

b) Kéo dài AA’ cắt đường tròn (O) tại điểm D. Chứng minh rằng tam giác CDH cân.

Ta có:

\(\begin{array}{l}\angle BAA' + \angle ABA' = {90^0}\\\angle BCC' + \angle ABA' = {90^0}\\ \Rightarrow \angle BAA' = \angle BCC'\end{array}\)

Lại có \(\angle BAA' = \angle BCD\) (cùng chắn cung \(BD\) )

\( \Rightarrow \angle BCC' = \angle BCD\left( { = \angle BAA'} \right)\)

Xét tam giác CDH có \(CA'\) vừa là đường cao vừa là đường phân giác nên là tam giác cân (đpcm).

Câu 5 (1,0 điểm)

Cách giải:

Cho \(ABCD\) là hình vuông có cạnh \(1dm.\) Trên cạnh \(AB\) lấy một điểm \(E.\) Dựng hình chữ nhật \(CEFG\) sao cho điểm \(D\) nằm trên cạnh \(FG.\) Tính diện tích hình chữ nhật \(CEFG\) (hình vẽ bên).

Ta có: \(\angle DCG = \angle BEC\) (cùng phụ với \(\angle DCE\))

Xét \(\Delta DCG\) và \(\Delta ECB\) có:

\(\angle G = \angle B = {90^0}\)

\(\angle DCG = \angle BEC\) (cmt)

Suy ra \(\Delta DCG \sim \Delta ECB\left( {g - g} \right)\)

\(\begin{array}{l} \Rightarrow \dfrac{{DC}}{{EC}} = \dfrac{{CG}}{{BC}}\\ \Rightarrow EC.CG = DC.BC = 1.1 = 1\end{array}\)

Suy ra \({S_{EFGC}} = EC.CG = 1d{m^2}\)