 Đề thi toán 6, đề kiểm tra toán 6 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
Đề thi toán 6, đề kiểm tra toán 6 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
 Đề thi học kì 2 Toán 6 Kết nối tri thức
Đề thi học kì 2 Toán 6 Kết nối tri thức Đề thi học kì 2 Toán 6 - Đề số 9
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Tính 2,8%2,8% của 5050
A. 1,41,4 B. 2,82,8 C. 1414 D. 2828
Câu 2. Trong hộp có 55 quả bóng xanh và 11 quả bóng đỏ. Không nhìn vào hộp, chọn ra từ hộp một quả bóng. Xét các sự kiện sau:
Sự kiện 1: Bóng chọn ra có màu vàng.
Sự kiện 2: Bóng chọn ra không có màu vàng.
Sự kiện 3: Bóng chọn ra có màu xanh.
Sự kiện nào có khả năng xảy ra cao nhất?
A. Sự kiện 1 B. Sự kiện 2
C. Sự kiện 3 D. Không có đáp án nào đúng
Câu 3. Nếu tung một đồng xu 2525 lần liên tiếp, có 1515 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
A. 2525 B. 3535 C. 2525 D. 1515
Câu 4. Cho bốn điểm A,B,C,DA,B,C,D như hình vẽ bên. Có bao nhiêu tia được tạo thành nếu mỗi tia đều chứa hai trong số các điểm đó?
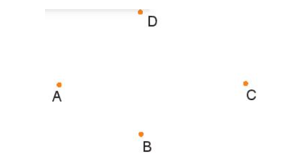
A. 44 B. 33 C. 1010 D. 1212
Phần II. Tự luận
Câu 1 Thực hiện các phép tính
A=−512−3:2,25;A=−512−3:2,25; B=(1512+3.736):(−22019);B=(1512+3.736):(−22019); C=−20232024.27−20232024.57+120232024C=−20232024.27−20232024.57+120232024
Câu 2 Tìm xx, biết:
a)x−23=76a)x−23=76 b)(43−x).(−56)=−73b)(43−x).(−56)=−73
Câu 3 Một khu vườn có diện tích 1000m21000m2 được chia thành các mảnh nhỏ để trồng cây ăn quả: bưởi, táo, cam, ổi. Diện tích trồng bưởi chiếm 25%25% tổng diện tích, diện tích trồng táo bằng 2525 diện tích còn lại, diện tích trồng cam và ổi bằng nhau. Tính diện tích trồng mỗi loại cây.
Câu 4 Cho đường thẳng xyxy, điểm OO thuộc đường thẳng xyxy. Trên tia OyOy lấy hai điểm AA và BB sao cho OA=3cm;OB=5cmOA=3cm;OB=5cm.
a) Tính độ dài đoạn thẳng ABAB.
b) Lấy điểm CC thuộc tia OxOx sao cho AC=6cmAC=6cm. Chứng tỏ OO là trung điểm của đoạn thẳng ACAC.
Câu 5 Tìm các số nguyên dương nn sao cho n260−nn260−n là một số nguyên tố.
Lời giải
Phần I: Trắc nghiệm
|
1. A |
2. B |
3. A |
4. D |
Câu 1
Phương pháp:
a%a% của bb bằng a.b100a.b100
Cách giải:
2,8%2,8% của 5050 bằng: 2,8.50100=1,42,8.50100=1,4
Chọn A.
Câu 2
Phương pháp:
Xét từng khả năng xảy ra của mỗi sự kiện.
Cách giải:
Sự kiện “Bóng Chọn ra có màu vàng” không thể xảy ra. Vì trong hộp không có quả bóng màu vàng.
Sự kiện "“Bóng Chọn ra không có màu vàng"”chắc chắn xảy ra vì trong hộp không có quả bóng màu vàng.
Trong hộp có cả quả bóng màu xanh và màu đỏ. Khi lấy ra một quả bóng từ trong hộp ra thì có thể lấy được số quả bóng màu xanh hoặc màu đỏ.
Do đó, sự kiện “Bóng Chọn ra có màu xanh” có thể xảy ra.
Vậy sự kiện có khả năng xảy ra cao nhất là “Bóng Chọn ra không có màu vàng”.
Chọn B.
Câu 3
Phương pháp:
Tính số lần xuất hiện mặt S.
Xác suất thực nghiệm xuất hiện mặt S là: số lần xuất hiện mặt S : số lần tung đồng xu.
Cách giải:
Số lần xuất hiện mặt S là: 25−15=1025−15=10 (lần)
Xác suất thực nghiệm xuất hiện mặt S là: 1025=251025=25
Chọn A.
Câu 4
Phương pháp:
Lần lượt chọn điểm A,B,CA,B,C làm gốc để vẽ được các tia.
Cách giải:
Chọn điểm AA làm điểm gốc thì có thể vẽ được 33 tia AB,AC,ADAB,AC,AD.
Chọn điểm BB làm điểm gốc thì có thể vẽ được 33 tia BA,BC,BDBA,BC,BD.
Chọn điểm CC làm điểm gốc thì có thể vẽ được 33 tia DA,DB,DCDA,DB,DC.
Vậy từ bốn điểm A,B,C,DA,B,C,D có 1212 tia được tạo thành.
Chọn D.
Phần II: Tự luận
Bài 1
Phương pháp:
Áp dụng các quy tắc :
+) Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc:
Lũy thừa →→ Nhân và chia →→ Cộng và trừ
+) Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc: ()→[]→{}()→[]→{}
Cách giải:
|
A=−512−3:2,25=−512−3:94=−512−3.49=−512−43=−512−1612=−2112=−74A=−512−3:2,25=−512−3:94=−512−3.49=−512−43=−512−1612=−2112=−74 B=(1512+3.736):(−22019)=(1712+3.736):(−22019)=(1712+712).2019−2=2412.2019−2=2.2019−2=−2019 |
|
C=−20232024.27−20232024.57+120232024=−20232024.27+−20232024.57+(1+20232024)=−20232024.(27+57)+1+20232024=−20232024.77+1+20232024=−20232024+1+20232024=−20232024+20232024+1=0+1=1 |
Bài 2
Phương pháp:
Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.
Cách giải:
|
a)x−23=76x=76+23x=116 Vậy x=116. |
b)(43−x).(−56)=−7343−x=−73:−5643−x=145x=43−145x=−2215 Vậy x=−2215. |
Bài 3
Phương pháp:
Áp dụng quy tắc: Muốn tìm mn của số b cho trước, ta tính b.mn(m,n∈N,n≠0).
Cách giải:
Diện tích trồng bưởi là: 1000.25%=250(m2)
Diện tích trồng 3 loại còn lại là: 1000−250=750(m2)
Diện tích trồng táo là: 750.25=300(m2)
Diện tích trồng cam là: (750−300):2=225(m2)
Vì diện tích trồng cam và ổi bằng nhau nên diện tích trồng ổi là 225m2.
Bài 4
Phương pháp:
a) Điểm A nằm giữa hai điểm O và B thì OA+AB=OB.
b) O là trung điểm của đoạn thẳng ACkhi điểm O nằm giữa hai điểm A và C, OC=OA.
Cách giải:
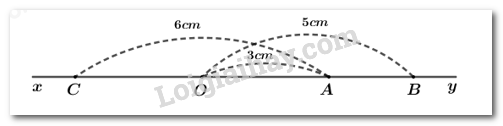
a) Tính độ dài đoạn thẳng AB.
Trên tia Oy, có OA<OB(3cm<5cm) nên điểm A nằm giữa hai điểm O và B.
Ta có: OA+AB=OB
⇒AB=OB−OA=5cm−3cm=2cm
Vậy AB=2cm.
b) Lấy điểm C thuộc tia Ox sao cho AC=6cm. Chứng tỏ O là trung điểm của đoạn thẳng AC.
Vì O thuộc đường thẳng xy nên Ox và Oy là hai tia đối nhau.
Ta có: C∈Ox; A∈Oy
Mà Ox và Oy là hai tia đối nhau
Suy ra, điểm O nằm giữa hai điểm A và C.
Vì điểm O nằm giữa hai điểm A và C nên ta có: OA+OC=AC
⇒OC=AC−OA=6cm−3cm=3cm
⇒OC=OA=3cm
Ta có:
+) Điểm O nằm giữa hai điểm A và C.
+) OC=OA
Suy ra, điểm O là trung điểm của đoạn thẳng AC.
Bài 5
Phương pháp:
Bước 1: Tìm các giá trị n∈Z+ để n260−n∈Z
Bước 2: Tìm các giá trị n∈Z+ để số nguyên n260−n là số nguyên tố.
Cách giải:
Với mọi n∈Z+ ta có: n260−n∈Z⇔n2⋮60−n.
Mà 60−n⋮60−n⇒n(60−n)⋮60−n
⇒60n−n2⋮60−n
Lại có: n2⋮60−n
⇒60n−n2+n2⋮60−n⇒60n⋮60−n
Có 60−n⋮60−n
⇒60(60−n)⋮60−n⇒3600−60n⋮60−n⇒60n+3600−60n⋮60−n⇒3600⋮60−n⇒60−n∈U(3600).
Mà U(3600)={±1;±2;±3;±4;.....}
Ta có: n∈Z+⇒60−n∈Z+⇒0<60−n≤60
Lại có: n260−n là số nguyên tố
+) Xét n260−n=2 ⇒n2=120−2n
⇒n2+2n−120=0⇒n2+12n−10n−120=0⇒n(n+12)−10(n+12)=0⇒(n−10)(n+12)=0⇒[n−10=0n+12=0⇒[n=10(tm)n=−12(ktm)
Với n=10 ta có n260−n là số nguyên tố.
+) Xét n260−n≠2⇒n260−n là các số nguyên tố lẻ và >2.
⇒n2,60−n cùng là hai số lẻ hoặc n2 chẵn và 60−n là số lẻ
⇒60−n là số lẻ.
⇒n260−n>2⇒n2+2n−120>0⇒(n−10)(n+12)>0⇒n>10⇒60−n<50.⇒60−n∈{1;3;9;15;25;45}
Ta có bảng giá trị:
|
60−n |
1 |
3 |
5 |
9 |
15 |
25 |
45 |
|
n |
59 |
57 |
58 |
51 |
45 |
35 |
15 |
|
n260−n |
3481 |
1083 |
1682 |
289 |
135 |
49 |
5 |
|
Nhận định |
ktm |
ktm |
ktm |
ktm |
ktm |
ktm |
tm |
⇒n=15 thì n260−n là số nguyên tố.
Vậy với n∈{10;15} thì n260−n là số nguyên tố.
- Đề thi học kì 2 Toán 6 - Đề số 10
- Đề thi học kì 2 Toán 6 - Đề số 11 - Kết nối tri thức
- Đề thi học kì 2 Toán 6 - Đề số 12 - Kết nối tri thức
- Đề thi học kì 2 Toán 6 - Đề số 13 - Kết nối tri thức
- Đề thi học kì 2 Toán 6 - Đề số 8
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 6 - Kết nối tri thức - Xem ngay

















