Đề thi giữa kì 1 Toán 6 - Đề số 17Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Tập hợp \({\mathbb{N}^*}\) được biểu diễn bằng?
Câu 2 :
Tìm x biết: \(178 - x:3 = 164\). Khi đó x bằng
Câu 3 :
Kết quả phép tính \({9^7}:{9^3}\) bằng
Câu 4 :
Kết quả phép tính \({4.5^2} - 81:{3^2}\) bằng
Câu 5 :
Công thức nào sau đây biểu diễn phép nhân hai lũy thừa cùng cơ số?
Câu 6 :
Nếu x là số tự nhiên sao cho \({\left( {x - 1} \right)^2} = 16\) thì x bằng
Câu 7 :
Số 600 phân tích ra thừa số nguyên tố là
Câu 8 :
Biểu thức 2.3.5 + 35 chia hết cho số nào sau đây?
Câu 9 :
Trong các tập hợp sau, tập hợp nào có các phần tử đều là số nguyên tố
Câu 10 :
Hãy chọn câu sai. Trong hình chữ nhật có:
Câu 11 :
Cho một hình vuông, hỏi nếu cạnh của hình vuông đã cho tăng gấp 3 lần thì diện tích của nó tăng gấp bao nhiêu lần?
Câu 12 :
Một hình thoi có diện tích bằng 24 cm2. Biết độ dài một đường chéo bằng 6 cm, tính độ dài đường chéo còn lại của hình thoi đó.
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Tập hợp \({\mathbb{N}^*}\) được biểu diễn bằng?
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về tập hợp số tự nhiên. Lời giải chi tiết :
Tập \({\mathbb{N}^*} = \left\{ {1;2;3;4;5.........} \right\}\). Các số phải cách nhau bởi dấu “;”. Đáp án D.
Câu 2 :
Tìm x biết: \(178 - x:3 = 164\). Khi đó x bằng
Đáp án : A Phương pháp giải :
Dựa vào quy tắc chuyển vế để tìm x. Lời giải chi tiết :
Ta có: \(\begin{array}{l}178 - x:3 = 164\\x:3 = 178 + 164\\x:3 = 342\\x = 342.3\\x = 1026\end{array}\) Vậy \(x = 1026\). Đáp án A.
Câu 3 :
Kết quả phép tính \({9^7}:{9^3}\) bằng
Đáp án : B Phương pháp giải :
Dựa vào kiến thức chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}\left( {a \ne 0;m \ge n \ge 0} \right)\). Lời giải chi tiết :
\({9^7}:{9^3} = {9^{7 - 3}} = {9^4}\). Đáp án B.
Câu 4 :
Kết quả phép tính \({4.5^2} - 81:{3^2}\) bằng
Đáp án : D Phương pháp giải :
Nếu phép tính có cả cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ. Lời giải chi tiết :
\({4.5^2} - 81:{3^2} = 4.25 - 81:9 = 100 - 9 = 91\) Đáp án D.
Câu 5 :
Công thức nào sau đây biểu diễn phép nhân hai lũy thừa cùng cơ số?
Đáp án : A Phương pháp giải :
Nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\). Lời giải chi tiết :
Công thức biểu diễn phép nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\). Đáp án A.
Câu 6 :
Nếu x là số tự nhiên sao cho \({\left( {x - 1} \right)^2} = 16\) thì x bằng
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về lũy thừa. Lời giải chi tiết :
\({\left( {x - 1} \right)^2} = 16\) \({\left( {x - 1} \right)^2} = {4^2}\) \(x - 1 = 4\) \(x = 4 + 1\) \(x = 5\) Vậy \(x = 5\). Đáp án C.
Câu 7 :
Số 600 phân tích ra thừa số nguyên tố là
Đáp án : A Phương pháp giải :
Phân tích một số ra thừa số nguyên tố bằng sơ đồ cây hoặc sơ đồ cột. Lời giải chi tiết :
Vậy \(600 = {2^3}{.3.5^2}\). Đáp án A.
Câu 8 :
Biểu thức 2.3.5 + 35 chia hết cho số nào sau đây?
Đáp án : C Phương pháp giải :
Dựa vào tính chất chia hết của một tổng. Lời giải chi tiết :
Vì \(\left( {2.3.5} \right) \vdots 5\) và \(35 \vdots 5\) nên \(\left( {2.3.5 + 35} \right) \vdots 5\). Đáp án C.
Câu 9 :
Trong các tập hợp sau, tập hợp nào có các phần tử đều là số nguyên tố
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về số nguyên tố. Lời giải chi tiết :
\(\left\{ {1;\,3;\,\,4;\,\,5;\,\,7} \right\}\) có 1 và 4 không phải số nguyên tố. \(\left\{ {1;2;\,\,3;\,\,\,5;\,\,7} \right\}\) có 1 không phải số nguyên tố. \(\left\{ {2;\,\,13;\,\,5;\,\,27} \right\}\) có 27 không phải số nguyên tố. Vì 2; 5; 13; 29 đều là số nguyên tố nên \(\left\{ {2;\,\,13;\,\,5;\,\,29} \right\}\) có tất cả phần tử đều là số nguyên tố. Đáp án D.
Câu 10 :
Hãy chọn câu sai. Trong hình chữ nhật có:
Đáp án : C Phương pháp giải :
Dựa vào đặc điểm của hình chữ nhật: - Các cạnh đối bằng nhau. - Hai đường chéo bằng nhau. Lời giải chi tiết :
Hình chữ nhật có hai cạnh đối song song và bằng nhau nên A, D đúng. Hình chữ nhật có hai đường chéo bằng nhau nên B đúng. Hình chữ nhật không có bốn cạnh bằng nhau nên C sai. Đáp án C.
Câu 11 :
Cho một hình vuông, hỏi nếu cạnh của hình vuông đã cho tăng gấp 3 lần thì diện tích của nó tăng gấp bao nhiêu lần?
Đáp án : D Phương pháp giải :
Sử dụng công thức tính diện tích hình vuông: S = cạnh . cạnh. Lời giải chi tiết :
Giả sử cạnh hình vuông ban đầu là \(x\). Khi đó diện tích hình vuông là \(x.x = {x^2}\). Nếu cạnh hình vuông tăng gấp 3 lần thì cạnh mới là \(3x\), khi đó diện tích hình vuông mới là \(3x.3x = 9{x^2}\). Diện tích của nó tăng gấp số lần là 9 lần. Đáp án D.
Câu 12 :
Một hình thoi có diện tích bằng 24 cm2. Biết độ dài một đường chéo bằng 6 cm, tính độ dài đường chéo còn lại của hình thoi đó.
Đáp án : B Phương pháp giải :
Dựa vào công thức tính diện tích hình thoi bằng \(\frac{1}{2}\) tích hai đường chéo để tính đường chéo còn lại. Lời giải chi tiết :
Độ dài đường chéo còn lại của hình thoi là: \(S = 24.2:6 = 8\left( {cm} \right)\) Đáp án B.
II. Tự luận
Phương pháp giải :
Sử dụng tính chất của phép tính với số tự nhiên. Nếu phép tính có cả cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ. Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\) Lời giải chi tiết :
a) \(146 + 121 + 54 + 379\) \(\begin{array}{l} = \left( {146 + 54} \right) + \left( {121\; + 379} \right)\\ = 200 + 500\\ = 700\end{array}\) b) \({2^3}.17-{2^3}.14\) \(\begin{array}{l} = {2^3}.\left( {17 - 14} \right)\\ = 8.3\\ = 24\end{array}\) c) \({5^{19}}:{5^{17}} + {3.3^3}-{7^0}\) \(\begin{array}{*{20}{l}}{ = {5^2} + {3^4}-1}\\\begin{array}{l} = \;25 + 81 - 1\\ = 105\end{array}\end{array}\) d) \(50-\left[ {\left( {20-{2^3}} \right):2} \right]\) \(\begin{array}{l} = 50-\left( {12:2} \right)\\ = 44\end{array}\) Phương pháp giải :
Sử dụng quy tắc chuyển vế kết hợp với các phép tính để tìm x. Lời giải chi tiết :
a) \(5.{\rm{x}} - 13 = 102\) \(\begin{array}{*{20}{l}}{5.x = 102 + 13}\\{5.x = {\rm{ }}115}\\{x = 115:5}\\{x = 23}\end{array}\) Vậy \(x = 23\). b) \(21 + {3^{{\rm{x}} - 2}} = 48\) \(\begin{array}{l}{3^{x - 2}} = 48 - 21\\{3^{x - 2}} = 27\\{3^{x - 2}} = {3^3}\\x - 2 = 3\\x = 3 + 2\\x = 5\end{array}\) Vậy \(x = 5\) c) \(2.x-14 = {5.2^3}\) \(\begin{array}{*{20}{l}}{2.x - 14 = 40}\\{2.x = 40 + 14}\\{2.x = 54}\\{x = 54:2}\\{x = 27}\end{array}\) Vậy \(x = 27\) Phương pháp giải :
Dựa vào dấu hiệu chia hết của 2; 5; 9. Lời giải chi tiết :
Vì \(\overline {4a12b} \) chia hết cho cả 2; 5 nên chữ số tận cùng là 0 hay \(b = 0\). Vì \(\overline {4a120} \) chia hết cho 9 nên \(4 + a + 1 + 2 + 0 = \left( {7 + a} \right)\; \vdots 9\). Mà \(0 \le a \le 9\) nên \(7 + a\) chỉ có thể bằng 9. Suy ra \(a = 9 - 7 = 2\) Vậy \(a = 2;b = 0\). Phương pháp giải :
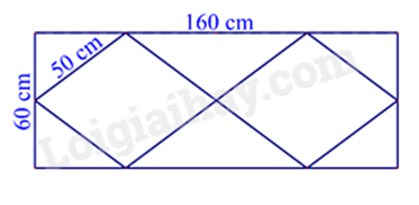
Sử dụng công thức tính chu vi hình chữ nhật, chu vi hình thoi. Chu vi hình chữ nhật = 2. (chiều dài + chiều rộng). Chu vi hình thoi = 4. cạnh. Lời giải chi tiết :
Chu vi hình chữ nhật là: \(2.(160 + 60) = 440(cm)\) Chu vi hình thoi là \(4.50.2 = 400(cm)\) Tổng chiều dài thanh thép là: \(440 + 400 + 10 = 850(cm)\) Đổi 850 cm = 8,5 m. Vậy chiều dài thanh thép ban đầu là 8,5 mét. Phương pháp giải :
Từ B tính \(3B\). Thực hiện phép tính \(3B - B\) để có \(2B\). Cộng 3, ta được \(2B + 3\). Mà \(2B + 3 = {3^n}\) nên ta tính được n. Lời giải chi tiết :
Ta có: \(B\;\; = 3 + {3^2} + {3^3} + ... + {3^{99}} + {3^{100}}\) Suy ra \(3B\; = {3^2} + {3^3} + ... + {3^{100}} + {3^{101}}\) Lấy 3B trừ B ta được: \(\begin{array}{l}3B\; - B\; = {3^2} + {3^3} + ... + {3^{100}} + {3^{101}} - \left( {3 + {3^2} + {3^3} + ... + {3^{99}} + {3^{100}}} \right)\\2B = {3^{101}} - 3\end{array}\) Do đó: \(2B + 3 = {3^{101}}\). Theo đề bài \(2B + 3 = {3^n}\) nên \(n = 101\). Vậy \(n = 101\).
|

























Danh sách bình luận