Đề thi học kì 1 Toán 6 - Đề số 6

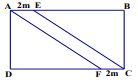
Đề bài

Phần I: Trắc nghiệm (4 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1:  Kết quả của phép tính 276 + 62 – 38 bằng:

A. 338

B. 262

C. 238

D. 300

Câu 2: Chữ số 8 trong số 968572 có giá trị bằng

A. 8 đơn vị

B. 8000 đơn vị

C. 8572 đơn vị

D. 968 đơn vị

Câu 3: Số đối của số 2021 là:

A. 2021

B. -2021

C. 0

D. –(-2021)

Câu 4: Tập hợp \(M = \left\{ {x \in \mathbb{Z}| - 3 \le x < 2} \right\}\) được viết dưới dạng liệt kê các phần tử là:

A. \(M = \left\{ { - 3; - 2; - 1;1} \right\}\)

B. \(M = \left\{ { - 2; - 1;0;1} \right\}\)

C. \(M = \left\{ { - 3; - 2; - 1;0;1} \right\}\)

D. \(M = \left\{ { - 3; - 2; - 1;0;1;2} \right\}\)

Câu 5: Nhiệt độ lúc 5 giờ sáng ở thủ đô Luân Đôn (nước Anh) là \( - {3^0}C\) . đếm 12 giờ cùng ngày nhiệt độ tăng thêm \({7^0}C\). Nhiệt độ lúc 12 giờ trưa cùng ngày ở thủ đô Luân Đôn là:

A. \({4^0}C\)

B. \({10^0}C\)

C. \( - {4^0}C\)

D. \( - {10^0}C\)

Câu 6: Cho hình bình hành ABCD có độ dài cạnh AB = 12 cm, cạnh BC = 9 cm. Chu vi hình hình hành ABCD là:

A. 21 cm

B. 42 cm²

C. 42 cm

D. 30 cm

Câu 7: Hình nào sau đây có đúng hai trục đối xứng?

A. Hình vuông

B. Hình bình hành

C. Hình thang cân

D. Hình thoi

Câu 8: Hình thang cân ABCD có đáy AB = 6cm, đáy CD dài hơn đáy AB là 5cm, chiều cao AH = 4cm. Diện tích hình thang cân ABCD là:

A. 34 cm²

B. 68 cm²

C. 22 cm²

D. 44 cm²

II. PHẦN TỰ LUẬN (6 điểm)

Câu 1: (1,5 điểm) Thực hiện phép tính:

a) 125 : 25 + 12.4

b) 25 – (62 – 75) + (-38)

c) 2680 + [10.(4³ – 54):5² + 2⁴]

Câu 2: (1,0 điểm) Tìm số nguyên x biết

a) 15x + 25 = 100

b) \(42 - \left[ {5x - \left( { - 32} \right)} \right] + 12:2 = 6\)

Câu 3: (1,0 điểm) Một nhân viên ở cửa hàng bán đồ ăn nhanh khi xếp số bánh ngọt vào các túi thì thấy rằng nếu xếp mỗi túi 10 chiếc, 12 chiếc hoặc 15 chiếc đều vừa đủ. Tính số bánh ngọt của cửa hàng biết rằng số bánh ngọt trong khoảng 100 đến 150 chiếc.

Câu 4: (2,0 điểm) Bác Nam có một khu đất hình chữ nhật ABCD chiều dài là 10m, chiều rộng bằng 6m. Bác Nam làm một lối đi bằng bê tông hình bình hành AECF và kích thước như hình vẽ, phần đất còn lại dùng để trồng hoa.

a) Tính chu vi và diện tích của khu đất hình chữ nhật.

b) Tính diện tích của lối đi bằng bê tông.

c) Biết tiền công để đổ một mét vuông bê tông là 25000 đồng, tiền công để trồng một mét vuông hoa ở khu đất còn lại là 15000 đồng. Hãy tính tổng số tiền để trả công cho việc đổ bê tông và trồng hoa?

Câu 5: (0,5 điểm) Chứng minh rằng hiệu \(\overline {abc}  - \overline {cba} \)  chia hết cho 11 (với a > c).

Lời giải

Phần I: Trắc nghiệm

Câu 1

Phương pháp:

Thực hiện phép tính theo thứ tự từ trái qua phải.

Cách giải:

276 + 62 – 38

= 338 – 38

= 300

Chọn D.

Câu 2

Phương pháp:

Xác định xem chữ số 8 đứng ở hàng nào.

Cách giải:

Trong số 968572, chữ số 8 đứng ở hàng nghìn nên có giá trị bằng 8000 đơn vị.

Chọn B.

Câu 3

Phương pháp:

Số đối của a là –a. Số đối của 0 là chính nó.

Cách giải:

Số đối của 2021 là -2021.

Chọn B.

Câu 4

Phương pháp:

Viết tập hợp dưới dạng liệt kê phần tử.

Cách giải:

Tập hợp \(M = \left\{ {x \in \mathbb{Z}| - 3 \le x < 2} \right\}\) được viết dưới dạng liệt kê các phần tử là \(M = \left\{ { - 3; - 2; - 1;0;1} \right\}\).

Chọn C.

Câu 5

Phương pháp:

Thực hiện quy tắc cộng hai số nguyên khác dấu.

Cách giải:

Nhiệt độ lúc 12 giờ trưa cùng ngày ở thủ đô Luân Đôn là:

\( - 3 + 7 = 4\,\,\left( {^0C} \right)\)

Chọn A.

Câu 6

Phương pháp:

Chu vi hình hành ABCD là (AB + BC).2

Cách giải:

Chu vi hình hành ABCD là

(AB + BC).2 = (12 + 9).2 = 42 (cm)

Chọn C.

Câu 7

Phương pháp:

Ghi nhớ các trục đối xứng của các hình:

- Hình vuông có 4 trục đối xứng.

- Hình hình hành không có trục đối xứng.

- Hình thang cân có 1 trục đối xứng.

- Hình thoi có 2 trục đối xứng.

Cách giải:

Hình thoi có 2 trục đối xứng là 2 đường chéo.

Chọn D.

Câu 8

Phương pháp:

- Tính chiều dài đáy CD.

- Tính diện tích hình thang bằng \(\dfrac{{\left( {AB + CD} \right).AH}}{2}\).

Cách giải:

Độ dài đáy CD là: \(6 + 5 = 11\,\,\left( {cm} \right)\)

Diện tích hình thang ABCD bằng: \(\dfrac{{\left( {AB + CD} \right).AH}}{2} = \dfrac{{\left( {6 + 11} \right).4}}{2} = 34\,\,\left( {c{m^2}} \right)\).

Chọn A.

II. PHẦN TỰ LUẬN

Câu 1

Phương pháp:

a) Thực hiện nhân chia trước, cộng trừ sau.

b) Thực hiện trong ngoặc trước, ngoài ngoặc sau.

c) Thực hiện lũy thừa trước, trong ngoặc trước, ngoài ngoặc sau, nhân chia trước, cộng trừ sau.

Cách giải:

a)

\(\begin{array}{l}\,\,\,\,125:25 + 12.4\\ = 5 + 48\\ = 53\end{array}\)

b)

\(\begin{array}{l}\,\,\,\,25 - \left( {62 - 75} \right) + \left( { - 38} \right)\\ = 25 - \left( { - 13} \right) - 38\\ = 25 + 13 - 38\\ = 38 - 38\\ = 0\end{array}\)

c)

\(\begin{array}{l}\,\,\,\,2680 + \left[ {10.\left( {{4^3}--54} \right):{5^2} + {2^4}} \right]\\ = 2680 + \left[ {10.\left( {64--54} \right):25 + 16} \right]\\ = 2680 + \left( {10.10:25 + 16} \right)\\ = 2680 + \left( {100:25 + 16} \right)\\ = 2680 + \left( {4 + 16} \right)\\ = 2680 + 20\\ = 2700\end{array}\) 

Câu 2

Phương pháp:

Giải bài toán tìm x

Cách giải:

a)

\(\begin{array}{l}15x + 25 = 100\\15x\,\,\,\,\,\,\,\,\,\,\, = 100 - 25\\15x\,\,\,\,\,\,\,\,\,\,\, = 75\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = 75:15\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = 5\end{array}\)

Vậy x = 5.

b) 

\(\begin{array}{l}42 - \left[ {5x - \left( { - 32} \right)} \right] + 12:2 = 6\\42 - \left( {5x + 32} \right) + 6 = 6\\42 - \left( {5x + 32} \right)\,\,\,\,\,\,\,\,\, = 6 - 6\\42 - \left( {5x + 32} \right)\,\,\,\,\,\,\,\,\, = 0\\\,\,\,\,\,\,\,\,\,\,\,\,5x + 32\,\,\,\,\,\,\,\,\,\,\, = 42 - 0\\\,\,\,\,\,\,\,\,\,\,\,\,5x + 32\,\,\,\,\,\,\,\,\,\,\, = 42\\\,\,\,\,\,\,\,\,\,\,\,\,5x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 42 - 32\\\,\,\,\,\,\,\,\,\,\,\,\,5x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 10\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 10:5\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2\end{array}\)

Vậy x = 2.

Câu 3

Phương pháp:

- Gọi số bánh ngọt là x \(\left( {x \in {\mathbb{N}^*},\,\,100 \le x \le 150} \right)\).

- Vì nếu xếp mỗi túi 10 chiếc, 12 chiếc hoặc 15 chiếc đều vừa đủ nên x là BC(10,12,15).

- Tìm BCNN(10,12,15). Suy ra BC(10,12,15).

- Tìm x là BC(10,12,15) thỏa mãn \(100 \le x \le 150\).

Cách giải:

Gọi số bánh ngọt là x \(\left( {x \in {\mathbb{N}^*},\,\,100 \le x \le 150} \right)\).

Vì nếu xếp mỗi túi 10 chiếc, 12 chiếc hoặc 15 chiếc đều vừa đủ nên x là BC(10,12,15).

Ta có:

\(\begin{array}{l}10 = 2.5\\12 = {2^2}.3\\15 = 3.5\end{array}\)

Suy ra \(BCNN\left( {10,12,15} \right) = {2^2}.3.5 = 60\)

Suy ra \(BC\left( {10,12,15} \right) = B\left( {60} \right) = \left\{ {0;60;120;180;...} \right\}\)

Mà \(100 \le x \le 150\) nên x = 120.

Vậy cửa hàng có 120 chiếc bánh ngọt.

Câu 4

Phương pháp:

a) Chu vi HCN =2. (chiều dài + chiều rộng)

 Diện tích HCN  = chiều dài . chiều rộng

b) Tính diện tích hình bình hành bằng cạnh nhân chiều cao tương ứng.

c) Tính diện tích khu đất trồng hoa.

Tính tiền công để trả cho việc trồng hoa.

Tính tiền công để trả cho việc đổ bê tông lối đi.

Tính tổng số tiền công phải trả.

Cách giải:

a) Chu vi của khu đất hình chữ nhật ABCD là:

(6 + 10).2 = 32 (m)

Diện tích của khu đất hình chữ nhật ABCD là:

6.10 = 60 (m²)

b) Lối đi là hình bình hành AECF có độ dài cạnh AE = 2m, chiều cao tương ứng là BC = 6m nên diện tích lối đi bằng bê tông là:

\(6.2 = 12\,\,\left( {{m^2}} \right)\)

c) Diện tích khu đất để trồng hoa là:

\(60 - 12 = 48\,\,\left( {{m^2}} \right)\)

Tiền công để trả cho việc trồng hoa là:

\(48.15000 = 720\,000\) (đồng)

Tiền công để trả cho việc đổ bê tông lối đi là:

\(12.25000 = 300\,000\) (đồng)

Tổng số tiền công phải trả là:

\(720\,000 + 300\,000\, = 1020\,000\) (đồng)

Câu 5

Phương pháp:

Phân tích \(\overline {abc}  = 100a + 10b + c\)

Chứng minh \(\overline {abc}  - \overline {cba} \) có dạng \(11k\).

Cách giải:

Ta có:

\(\begin{array}{l}\,\,\,\,\overline {abc}  - \overline {cba} \\ = 100a + 10b + c - \left( {100c + 10b + a} \right)\\ = 100a + 10b + c - 100c - 10b - a\\ = 99a - 99c\\ = 11\left( {9a - 9c} \right)\end{array}\)

Vì \(11\,\, \vdots \,\,11\) nên \(11\left( {9a - 9c} \right)\,\, \vdots \,\,11\).

Vậy hiệu \(\overline {abc}  - \overline {cba} \) cũng chia hết cho 11 (đpcm).