Đề thi, đề kiểm tra Toán lớp 6 - Kết nối tri thức

Đề thi học kì 1 Toán 6 - Đề số 14

Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên...

Tải về

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án
Làm đề thi

Phần trắc nghiệm (3 điểm) Câu 1: Cho hình bình hành ABCD có AB = 5 cm, BC = 8 cm thì:

Đề bài

I. Trắc nghiệm
Câu 1 :

Cho hình bình hành  ABCD có AB = 5 cm, BC = 8 cm thì:

  • A
    CD = 5 cm.
  • B
    AC = 8cm.
  • C
    CD = 8 cm.
  • D
    AC = 5 cm.
Câu 2 :

Điền vào chỗ “…” trong phát biểu sau để được phát biểu đúng:

“ 729 chia hết cho 9 vì …”

  • A
    có chữ số tận cùng là 9 chia hết cho 9.
  • B
    có hai chữ số đầu tiên là 72 chia hết cho 9.
  • C
    tổng các chữ số là (7+2+9)=18, tổng này chia hết cho 9.
  • D
    Tất cả đều đúng
Câu 3 :

Tính chất nào sau đây không phải của hình chữ nhật?

  • A
    Hai cặp cạnh đối diện bằng nhau.                
  • B
    Hai cặp cạnh đối diện song song.
  • C
    Hai đường chéo vuông góc với nhau.
  • D
    Có 4 góc vuông.
Câu 4 :

Số nào sau đây không phải là số nguyên tố:

  • A
    17.
  • B
    13.
  • C
    39.
  • D
    43.
Câu 5 :

Tập hợp tất cả các  ước của - 12 là:

  • A
    \(\left\{ { - 12; - 6; - 4; - 3; - 2; - 1} \right\}\).
  • B
    \(\left\{ {6;4;3;0} \right\}\).
  • C
    \(\left\{ {12; - 12;6; - 6;4; - 4;3; - 3;2; - 2;1; - 1} \right\}\).
  • D
    \(\left\{ {0;12;24;36} \right\}\).
Câu 6 :

Chọn phát biểu sai.

  • A
    Tổng hai số nguyên dương là số nguyên dương.
  • B
    Tổng hai số nguyên âm là số nguyên âm.
  • C
    Tổng hai số nguyên đối nhau là 0.
  • D
    Tổng hai số nguyên khác dấu là số nguyên dương.
Câu 7 :

Khẳng định nào dưới đây sai?

  • A
    Số đối của –2 là 2.
  • B
    Số đối của 13 là – (–13).
  • C
    Số đối của số 9 là –9.
  • D
    Số đối của –2019 là  2019.
Câu 8 :

Hình nào dưới đây có trục đối xứng

  • A
    Hình bình hành.
  • B
    Hình tam giác.
  • C
    Hình thang vuông.
  • D
    Hình thang cân.
Câu 9 :

Khẳng định nào sau đây là sai?

  • A
    Hình vuông có hai đường chéo vuông góc.           
  • B
    Hình thang cân có hai đường chéo bằng nhau.
  • C
    Tam giác đều là tam giác có ba cạnh bằng nhau.  
  • D
    Hình thoi có bốn góc vuông bằng nhau.
Câu 10 :

Trong các hình sau, có bao nhiêu hình có tâm đối xứng:

  • A
    1.
  • B
    2.
  • C
    3.
  • D
    4.
Câu 11 :

Tìm số nguyên a, biết số liền sau a là một số nguyên dương và số liền trước a là một số nguyên âm

  • A
    0.
  • B
    -2.
  • C
    -1.
  • D
    1.
Câu 12 :

Kết quả phép tính: \(\left( { - 1} \right).2 - 3.4 + 5.6\) là:

  • A
    16.
  • B
    17.
  • C
    19.
  • D
    27.
II. Tự luận
Câu 1 :

Thực hiện phép tính:

a) \(256 + ( - 156)\)

b) \(35.\left( { - 28} \right) + 35.\left( { - 70} \right) + 35.\left( { - 2} \right)\)
Câu 2 :

Tìm x, biết: \(1080{\rm{ : }}x =  - {\rm{ }}40.\)
Câu 3 :

Số học sinh khối 6 của trường THCS A trong khoảng từ 500 đến 560 học sinh. Biết khi xếp thành hàng 12, hàng 15, hàng 18 đều vừa đủ. Tính số học sinh khối 6 của trường THCS A.
Câu 4 :

Một toà nhà có 35 tầng và 3 tầng hầm (tầng G được đánh số là tầng 0), một thang máy đang ở tầng 5, sau đó nó đi lên 23 tầng và rồi đi xuống 27 tầng. Hỏi lúc này thang máy đang dừng lại tại tầng mấy?
Câu 5 :

Bác Năm có một mảnh vườn hình chữ nhật với chiều dài 10 mét và chiều rộng là 8 mét. Giữa mảnh vườn, bác Năm dành một miếng đất hình vuông cạnh 7 mét để trồng rau, phần còn lại chừa lối đi xung quanh.            

a) Tính diện tích trồng rau.

b) Lối đi được lát sỏi, chi phí mỗi mét vuông hết 110 000 đồng.

Hỏi chi phí làm lối đi là bao nhiêu?
Câu 6 :

Một chiếc bàn hình chữ nhật, biết rằng đường chéo dài 1,5 m, em hãy tính khoảng cách từ tâm đối xứng của mặt bàn đến mỗi đỉnh.

Lời giải và đáp án

I. Trắc nghiệm
Câu 1 :

Cho hình bình hành  ABCD có AB = 5 cm, BC = 8 cm thì:

  • A
    CD = 5 cm.
  • B
    AC = 8cm.
  • C
    CD = 8 cm.
  • D
    AC = 5 cm.

Đáp án : A

Phương pháp giải :

Dựa vào đặc điểm của hình bình hành.

Lời giải chi tiết :

Hình bình hành có các cạnh đối bằng nhau nên AB = CD = 5 cm; BC = AD = 8 cm.

Câu 2 :

Điền vào chỗ “…” trong phát biểu sau để được phát biểu đúng:

“ 729 chia hết cho 9 vì …”

  • A
    có chữ số tận cùng là 9 chia hết cho 9.
  • B
    có hai chữ số đầu tiên là 72 chia hết cho 9.
  • C
    tổng các chữ số là (7+2+9)=18, tổng này chia hết cho 9.
  • D
    Tất cả đều đúng

Đáp án : C

Phương pháp giải :

Dựa vào dấu hiệu chia hết cho 9: Các số có tổng các chữ số chia hết cho 9 thì số đó chia hết cho 9 và chỉ những số đó chia hết cho 9.

Lời giải chi tiết :

Ta có: 7 + 2 + 9 = 18 \( \vdots \) 9 nên 729 chia hết cho 9 => đáp án C.

Câu 3 :

Tính chất nào sau đây không phải của hình chữ nhật?

  • A
    Hai cặp cạnh đối diện bằng nhau.                
  • B
    Hai cặp cạnh đối diện song song.
  • C
    Hai đường chéo vuông góc với nhau.
  • D
    Có 4 góc vuông.

Đáp án : C

Phương pháp giải :

Hình chữ nhật có:

- Hai cặp cạnh đối diện bằng nhau

- Hai cặp cạnh đối diện song song

- Bốn góc ở đỉnh bằng nhau và bằng góc vuông.

- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Lời giải chi tiết :

Hai đường chéo của hình chữ nhật không vuông góc với nhau nên C sai.

Câu 4 :

Số nào sau đây không phải là số nguyên tố:

  • A
    17.
  • B
    13.
  • C
    39.
  • D
    43.

Đáp án : C

Phương pháp giải :

Dựa vào kiến thức về số nguyên tố: Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó.

Lời giải chi tiết :

Ta có:

Ư(17) = {1; 17}

Ư(13) = {1; 13}

Ư(39) = {1; 3; 13; 39}

Ư(43) = {1; 43}

=> 39 không phải là số nguyên tố.

Câu 5 :

Tập hợp tất cả các  ước của - 12 là:

  • A
    \(\left\{ { - 12; - 6; - 4; - 3; - 2; - 1} \right\}\).
  • B
    \(\left\{ {6;4;3;0} \right\}\).
  • C
    \(\left\{ {12; - 12;6; - 6;4; - 4;3; - 3;2; - 2;1; - 1} \right\}\).
  • D
    \(\left\{ {0;12;24;36} \right\}\).

Đáp án : C

Phương pháp giải :

Liệt kê các ước của -12.

Lời giải chi tiết :

Ư(-12) = \(\left\{ {12; - 12;6; - 6;4; - 4;3; - 3;2; - 2;1; - 1} \right\}\)

Câu 6 :

Chọn phát biểu sai.

  • A
    Tổng hai số nguyên dương là số nguyên dương.
  • B
    Tổng hai số nguyên âm là số nguyên âm.
  • C
    Tổng hai số nguyên đối nhau là 0.
  • D
    Tổng hai số nguyên khác dấu là số nguyên dương.

Đáp án : D

Phương pháp giải :

- Tổng của hai số nguyên dương là số nguyên dương.

- Tổng của hai số nguyên âm là số nguyên âm.

- Hai số nguyên đối nhau có tổng bằng 0: a +(-a) = 0.

Lời giải chi tiết :

Dựa vào các nhận xét về phép cộng hai số nguyên, ta thấy đáp án D sai.

Câu 7 :

Khẳng định nào dưới đây sai?

  • A
    Số đối của –2 là 2.
  • B
    Số đối của 13 là – (–13).
  • C
    Số đối của số 9 là –9.
  • D
    Số đối của –2019 là  2019.

Đáp án : B

Phương pháp giải :

Số đối của a là –a.

Lời giải chi tiết :

Số đối của – 2 là 2 nên A đúng.

Số đối của 13 là – 13 nên B sai.

Số đối của 9 là -9 nên C đúng.

Số đối của – 2019 là – ( - 2019) = 2019 nên D đúng.

Câu 8 :

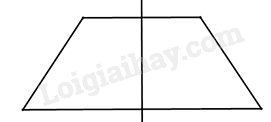
Hình nào dưới đây có trục đối xứng

  • A
    Hình bình hành.
  • B
    Hình tam giác.
  • C
    Hình thang vuông.
  • D
    Hình thang cân.

Đáp án : D

Phương pháp giải :

Dựa vào kiến thức về trục đối xứng: Có một đường thẳng d chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau.

Lời giải chi tiết :

Hình thang cân có trục đối xứng.

Câu 9 :

Khẳng định nào sau đây là sai?

  • A
    Hình vuông có hai đường chéo vuông góc.           
  • B
    Hình thang cân có hai đường chéo bằng nhau.
  • C
    Tam giác đều là tam giác có ba cạnh bằng nhau.  
  • D
    Hình thoi có bốn góc vuông bằng nhau.

Đáp án : D

Phương pháp giải :

Dựa vào tính chất của các hình đã học.

Lời giải chi tiết :

Hình vuông có hai đường chéo vuông góc nên A đúng.

Hình thang cân có hai đường chéo bằng nhau nên B đúng.

Tam giác đều là tam giác có ba cạnh bằng nhau nên C đúng.

Hình thoi có các góc đối bằng nhau, không phải bốn góc vuông bằng nhau nên D sai.

Câu 10 :

Trong các hình sau, có bao nhiêu hình có tâm đối xứng:

  • A
    1.
  • B
    2.
  • C
    3.
  • D
    4.

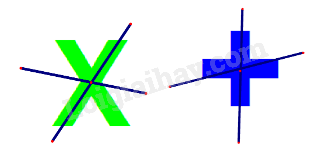
Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về tâm đối xứng: Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.

Lời giải chi tiết :

Hình a và hình b là hình có tâm đối xứng.

Vậy có 2 hình có tâm đối xứng.

Câu 11 :

Tìm số nguyên a, biết số liền sau a là một số nguyên dương và số liền trước a là một số nguyên âm

  • A
    0.
  • B
    -2.
  • C
    -1.
  • D
    1.

Đáp án : A

Phương pháp giải :

Dựa vào kiến thức về số nguyên.

Lời giải chi tiết :

Số nguyên a mà số liền sau a là một số nguyên dương và số liền trước a là một số nguyên âm là số 0.

Câu 12 :

Kết quả phép tính: \(\left( { - 1} \right).2 - 3.4 + 5.6\) là:

  • A
    16.
  • B
    17.
  • C
    19.
  • D
    27.

Đáp án : A

Phương pháp giải :

Sử dụng các quy tắc tính với số nguyên.

Lời giải chi tiết :

Ta có: \(\left( { - 1} \right).2 - 3.4 + 5.6 =  - 2 - 12 + 30 =  - 14 + 30 = 30 - 14 = 16\)

II. Tự luận
Câu 1 :

Thực hiện phép tính:

a) \(256 + ( - 156)\)

b) \(35.\left( { - 28} \right) + 35.\left( { - 70} \right) + 35.\left( { - 2} \right)\)
Phương pháp giải :

Sử dụng quy tắc tính với số nguyên.

Lời giải chi tiết :

a) \(256 + ( - 156)\)

\(\begin{array}{l} = 256 - 156\\ = 100\end{array}\)

b) \(35.\left( { - 28} \right) + 35.\left( { - 70} \right) + 35.\left( { - 2} \right)\)

\(\begin{array}{l} = 35.\left( { - 28 - 70 - 2} \right)\\ = 35.( - 100)\\ =  - 3500\end{array}\)

Câu 2 :

Tìm x, biết: \(1080{\rm{ : }}x =  - {\rm{ }}40.\)
Phương pháp giải :

Sử dụng quy tắc chia hai số nguyên khác dấu.

Lời giải chi tiết :

1080 : x = -40

x = 1080 : (-40)

x = -(1080 : 40)

x = -27.

Vậy x = -27.

Câu 3 :

Số học sinh khối 6 của trường THCS A trong khoảng từ 500 đến 560 học sinh. Biết khi xếp thành hàng 12, hàng 15, hàng 18 đều vừa đủ. Tính số học sinh khối 6 của trường THCS A.
Phương pháp giải :

Gọi a là số học sinh cần tìm. (học sinh) (\(a \in BC\left( {12;15;18} \right)\) và \(500 < a < 600\))

+ Tìm BCNN(12; 15; 18).

+ BC(12; 15; 18) là tập hợp bội của BCNN(12; 15; 18).

+ Chọn trong số đó bội thỏa mãn điều kiện đã cho.

Lời giải chi tiết :

Gọi a là số học sinh cần tìm. (\(a \in BC\left( {12;15;18} \right)\) và \(500 < a < 560\))

Ta có: \(12 = {2^2}.3;15 = 3.5;18 = {2.3^2}\)

\( \Rightarrow BCNN\left( {12;15;18} \right) = {2^2}{.3^2}.5 = 180\)

\(BC\left( {12;15;18} \right) = \left\{ {0;180;360;540;720; \ldots } \right\}\)

Vì \(500 < a < 560\) nên \(a = 540\).

Vậy số học sinh khối 6 là 540 em.

Câu 4 :

Một toà nhà có 35 tầng và 3 tầng hầm (tầng G được đánh số là tầng 0), một thang máy đang ở tầng 5, sau đó nó đi lên 23 tầng và rồi đi xuống 27 tầng. Hỏi lúc này thang máy đang dừng lại tại tầng mấy?
Phương pháp giải :

Viết phép tính biểu thị tầng mà thang máy dừng lại.

Lời giải chi tiết :

Lúc đầu thang máy ở tầng 5.

Thang máy đi lên 23 tầng: + 23.

Thang máy đi xuống 27 tầng: - 27.

=> Ta có phép tính: 5 + 23 – 27 = 1.

Vậy thang máy dừng lại ở tầng 1.

Câu 5 :

Bác Năm có một mảnh vườn hình chữ nhật với chiều dài 10 mét và chiều rộng là 8 mét. Giữa mảnh vườn, bác Năm dành một miếng đất hình vuông cạnh 7 mét để trồng rau, phần còn lại chừa lối đi xung quanh.            

a) Tính diện tích trồng rau.

b) Lối đi được lát sỏi, chi phí mỗi mét vuông hết 110 000 đồng.

Hỏi chi phí làm lối đi là bao nhiêu?
Phương pháp giải :

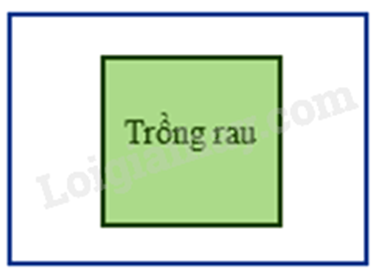
a) Sử dụng công thức tính diện tích hình vuông để tính diện tích trồng rau.

b) Tính diện tích mảnh vườn (sử dụng công thức tính diện tích hình chữ nhật).

Diện tích lối đi bằng diện tích mảnh vườn – diện tích trồng rau.

Chi phí làm lối đi bằng chi phí mỗi mét vuông . diện tích lối đi.

Lời giải chi tiết :

a) Diện tích trồng rau là: \(7.7 = 49\left( {{m^2}} \right)\)

b) Diện tích mảnh vườn là: \(10.8 = 80\left( {{m^2}} \right)\)

Diện tích lối đi: \(10.8 - 49 = 31\left( {{m^2}} \right)\)

Chi phí làm lối đi: \(31.\;110\;000 = 3\;410\;000\) (đồng)

Vậy a) Diện tích trồng rau là 49m2.

b) Chi phí làm lối đi là 3 410 000 đồng.

Câu 6 :

Một chiếc bàn hình chữ nhật, biết rằng đường chéo dài 1,5 m, em hãy tính khoảng cách từ tâm đối xứng của mặt bàn đến mỗi đỉnh.
Phương pháp giải :

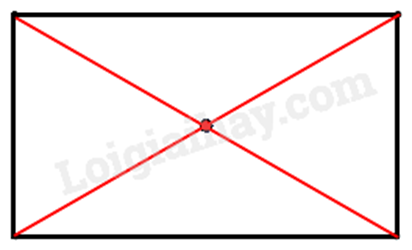
Dựa vào kiến thức về tâm đối xứng của hình chữ nhật: Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.

Lời giải chi tiết :

Vì mặt bàn là một hình chữ nhật nên tâm đối xứng là giao điểm của đường chéo được minh họa như sau:

Do đó độ dài đường chéo gấp 2 lần khoảng cách từ tâm đối xứng đến mỗi đỉnh

Khoảng cách từ tâm đối xứng đến mỗi đỉnh là: 1,5 : 2 = 0,75 (m). 

Bài liên quan
close